油气水三相流相含率超声测试模型优化

苏茜，邓翔天，刘振兴

（1 武汉科技大学信息科学与工程学院（人工智能学院），湖北 武汉 430081；2 武汉科技大学冶金自动化与检测技术教育部工程研究中心，湖北 武汉 430081）

油气水三相流动现象常见于石油和天然气工业过程中，如在低压和低渗透率油藏开采过程中，为了提高石油采收率，将二氧化碳注入储层，从而降低石油黏度，促进石油与岩石表面分离[1]，注入的二氧化碳与石油以及储层中的原生水混合，形成石油-二氧化碳-水三相流。通常，石油和天然气的混合输送中，管线压力降低可能导致湿气逆向冷凝形成自由水[2]，呈现具有低液体负载的石油-天然气-水三相流动。深入了解油气水三相流的流动特性，如流型、压降和相含率等参数，对优化油田的生产设计、延长油田使用寿命具有重要意义。相含率是多相流参数测量的重要指标之一，分相含率的准确测量为流型、流速、混合密度和传热传质等参数的研究提供了理论指导。此外，湿气管道中液体的存在可能导致冻结、腐蚀和水合物形成等问题，实时预测相含率对于管道的正确设计和操作尤为重要。

气相表观速度远大于油、水相表观速度的工况下，水基分散分层流是油气水三相流常见流型，其流动特征为：油滴作为分散相分散于连续水相中，气相与液相分层。受油水两相相互作用和分散相分布的影响，与气液两相流相比，油气水三相流流动特性更为复杂，为油气水三相流相含率测量带来挑战。相含率测量技术主要有电学法[3]、射线法[4]、微波法[5]、光学法[6]和超声法[7]等，与其他技术相比，超声波能够穿透不透光材料，且其测量过程中不需要稀释流体，适用于高浓度分散系统的参数表征，具有非侵入性优势[8]。

基于超声方法，针对水基分散分层流相含率的研究，学者们开展了分散两相流体系相含率和粒径分布的研究工作。苏茜等[7]基于有限元方法，讨论了油水两相流相分布和相含率与超声波衰减系数之间的关系。邵一哲等[9]采用多频超声测量方法，对于不同含油率和颗粒粒度情况下的油水分散流，分析了BLBL模型描述超声衰减的的适用性。Yu等[10]考虑了液滴非均匀分布对超声衰减的影响，提出分形方法修正声衰减模型，建立了含油率和超声衰减的关系。Liang 等[11]为研究油水乳状液的超声回波衰减特性，在不同含水率和搅拌速度工况下开展了实验，结果表明超声回波对油水反相过程十分敏感。应启帆等[12]基于ECAH（Epstein-Carhart-Allegra-Hawley）超声衰减模型，建立了一种预测悬移质粒径分布的多输出回归模型，并验证了算法的准确度。Silva等[13]分析了油包水乳状液的超声频谱，通过将耦合相理论与弹性散射理论相结合，有效估计了液滴尺寸双峰分布。Mei 等[14]考虑了非长波长区粘度损失和散射损失对超声衰减的主导作用，提出了McCBLBL 模型（McClements 模型结合BLBL 模型），用于测量水滴和空气分别为分散相和连续相时的颗粒分布。Shi 等[15]将脉冲回波技术、多普勒技术以及电导技术相结合，为使用多模态传感器测量油气水多相流分相流量提供了理论指导。然而，现有超声测试模型对换能器测量信息利用有限，且没有深入考虑超声衰减模型的适用性问题，忽略了液相中分散相相含率改变对混合声速的影响。

本文针对上述问题，首先根据有效粒径模型，确定油水分散流中超声散射衰减机制；其次，基于超声衰减机理，采用有限元仿真，探究水基分散分层流中超声扩散衰减的估计方法，在此基础上，推导含油率超声测试模型；最后，通过建立与超声波传播路径相关的修正参数，改进油水分散流中混合声速模型，从而建立含气率优化模型，提高油气水多相流相含率超声测试精度。

1 超声波传播理论

1.1 超声透射衰减机理

超声波在介质中传播，声波能量随着传播距离的增加而降低，即超声波的衰减现象[16]。考虑沿特定方向传播的平面声波，超声波能量的耗散程度可以采用超声衰减系数表征，如式(1)。

式中，pe和pr分别为超声发射端和接收端声压；α为超声衰减系数；l为超声波传播的路径长度。

超声波与油水分散系统相互作用，主要包括四种衰减机制[16]：固有吸收、黏惯性耦合、热耦合和散射。

（1）固有吸收

流体中超声波的吸收衰减主要由热扩散和黏性耗散效应引起，根据Stokes-Kirchhoff 经典关系式，声吸收衰减如式(2)。

式中，αS-K为单相流体中超声吸收衰减系数；f为超声波频率；c为压缩波波速；ρ为流体密度；μb和μs分别为流体体积黏度和剪切黏度；κ为流体热导率；cv和cp分别为流体定容比热容和定压比热容。

油水两相流中，cp≈cv，即与黏性分量相比，热分量可以忽略。根据Cicchitti 两相黏度模型[17]，油水两相流中超声吸收衰减系数简化为式(3)。

式中，αint为油水两相流中超声吸收衰减系数；η=μb+4μs/3 为流体纵向黏度；φd为分散相含率；下标c、d 和m 分别表示连续相、分散相和油水混合物；cm为油水混合物中声速。

由式(3)可知，超声波吸收衰减程度与超声波频率以及介质本身属性有关，且受油水两相流中分散相浓度和混合声速的影响，而与分散相颗粒的尺寸无关。

（2）黏惯性耦合

由于分散相与连续相存在密度差异，颗粒与周围液体间存在滑动摩擦力，液体对颗粒的黏性阻力抑制了颗粒的运动，导致部分超声能量转化为热能。

（3）热耦合

声场中的压力-温度耦合作用导致压力与温度发生波动。由于油相的热容小于水相，油滴内部温度波动程度比水中更大。在油滴的压缩或膨胀过程中，部分超声能量转化为热能。

（4）散射

油水分散流中，超声波在油水两相界面处发生散射现象，使得超声波偏离原始传播路径，导致换能器无法接收到部分超声波，此时，超声能量并没有耗散。超声波的散射行为主要取决于分散相颗粒半径（R）和超声波波长（λ）之比，用量纲为1波数（kcR）表示为式(4)。

式中，kc为连续相中压缩波波数；ω=2πf为角频率。

Faran 弹性散射模型[18]适用于油水分散体系中颗粒尺寸处于中波长区（kcR～1）时超声散射衰减的预测。根据Hay & Mercer 理论[19]，剪切波无法在水基分散分层流系统中传播，油滴球表面剪切应力的切向分量为零，超声散射衰减系数为每个颗粒散射系数的总和表示为式(5)。

式中，αsca为超声散射衰减系数；Un为n阶散射系数；Re表示取实部。

热耗散和黏惯性耗散发生在颗粒与周围流体之间的界面处，是长波长区（kcR≪1）主要的衰减机制，而散射则主导着非长波长区超声的衰减。

随着超声波传播距离增加，声束波阵面的扩展导致超声波能量逐渐削弱，此外分散相对声束的多重散射作用改变了波阵面形状，导致使用单个换能器得到的超声衰减测量值与实际值存在偏差，因此超声扩散衰减对总超声衰减的贡献不能忽略[20]。假设上述衰减机制相互独立，忽略热机制和黏惯性机制的贡献，则总超声衰减为超声吸收衰减、散射衰减和扩散衰减的线性叠加，如式(6)。

式中，αtot为总超声衰减系数；αdiff为超声扩散衰减系数。

1.2 脉冲回波测试原理

气、液两相声阻抗差异很大，超声波传播遇到气液界面时，几乎发生超声波的全反射[21]。根据气液界面处超声波的反射特性，通常采用超声波脉冲回波法测量介质衰减特性，脉冲回波测试原理如图1。图1测试系统选用收发一体型超声换能器，即换能器同时作为超声激励端和接收端，则气液界面高度如式(7)。

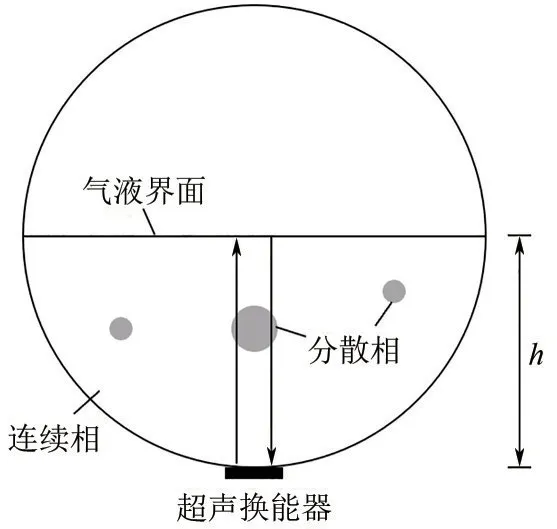
图1 脉冲回波法测试原理

式中，h为气液界面高度；t为超声波脉冲的渡越时间。

2 有效粒径模型

为了确定kcR范围，采用Brauner 最大粒径模型[22]预测油水分散流中油滴尺寸分布。由Hinze 理论可知，液液两相分散体系中，分散相颗粒粒径与分相流量有关，随着分散相体积分数的增大，可能发生液滴的破碎和聚并现象，则有式(8)、式(9)。

式中，dmax为油滴最大粒径；D为管道内径；εd为分散相体积分数；σ为油水界面张力；u为流体速度；F为Fanning摩擦因子；Rec为连续相雷诺数；do为油滴有效粒径；d32为油滴Sauter 平均粒径；CH和kd均为可调常量，对于水包油油水分散流，CH和kd可分别取值为0.226和1.551[23]。

考虑水平管道中充分发展的水基分散分层流，将油滴有效直径模型式(8)和式(9)代入油气水三相动量守恒方程[15]，保持气相和油相流量不变，求解得到不同水相流量条件下气液界面高度、含油率和粒径的变化如图2所示。可以看出，随着水相流量的增加，油水两相混合流量增加，液相占据的体积随之增大，导致气液界面高度增大；同时，液相中含油率减小，分散油滴之间的碰撞频率降低，连续相的湍流作用增强，导致油滴发生破碎现象，油滴粒径减小，数量增多，这与油水分散流中趋势一致[24]。由图2可知，对应工况下，水基分散分层流中油滴有效半径的范围为0.244～1.096mm。

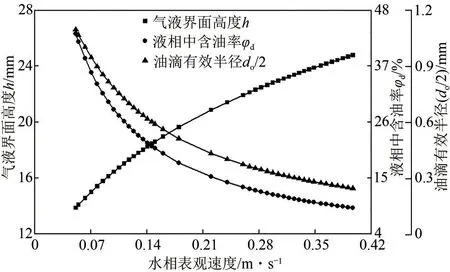
图2 不同水相表观速度下气液界面高度、含油率和粒径变化（气相和油相表观速度分别为7m/s和0.04m/s）

3 超声测试仿真模型

为了获得水基分散分层流的截面声场分布，基于有限元方法，利用多物理场耦合软件COMSOL Multiphysics®建立管道二维几何剖分模型。超声换能器采用一发三收测量模式，其中，T/R为自发自收型换能器，R1和R2为接收型换能器，换能器安装夹角为22.5°。设置换能器半径（a）为4.5mm，管道内径为50mm。超声脉冲发射频率设置为f=1MHz。为了保证超声波换能器的距离分辨率，选择远场作为气液界面高度测量区域，参考气液界面高度（href）设置为22mm，气相和液相使用线段分离。液相中油滴的尺寸分布采用单分散尺寸分布模型，根据上述分析可知，kcR对应范围为1.035～4.649，这里将油滴半径设置为0.4mm 进行讨论。有限元网格采用自由三角形方案生成，为了均衡仿真精度和计算成本，网格最大尺寸设置为λ/6。仿真物理模型和网格划分分别如图3(a)和(b)所示，仿真所用油气水三相相关参数分别列于表1。

表1 多相流相关参数（温度293.15/K）

图3 仿真物理模型及其有限元网格划分

在图3(a)单分散系统中，假设球形油滴的空间分布相对均匀，边长为（2R+ΔR）的正方形内部分散相占据面积为πR2，则油滴间平均距离（ΔR）估算为式(10)[25]。

超声波发射端采用声-结构耦合模式，接收端设置二维截线接收由气液界面反射的回波信号。选用周期性正弦脉冲信号作为激励信号，如式(11)。

式中，A为激励信号g(t)幅值；np为脉冲循环数。激励信号的时域及频域如图4所示。

图4 激励信号的时域及频域（np = 5）

4 水基分散分层流相含率建模及优化

4.1 含油率超声测试模型建立

保持气液界面高度不变，通过改变油滴数量和油滴间距离，得到不同含油率分布的水基分散分层流流型。提取超声换能器接收端声压信号，运用快速傅里叶变换技术（FFT）得到对应频域内声压信号幅值。

为了计算超声扩散衰减对总超声衰减的贡献，MURAI 提出了气液界面反射声压有效比公式[21]，然而由于超声波能量沿波阵面切向分布不均匀，采用该方法估计超声扩散衰减准确度较低；此外，基于坐标的积分方法需要求解多个空间坐标点的声压分布[20,26]。鉴于以上问题，结合换能器收发方式，提出以下公式估计超声扩散衰减系数，见式(12)、式(13)。

式中，E0、E1和E2分别为换能器T/R、R1和R2接收端测量声强的分配比例；p0、p1和p2分别为换能器T/R、R1和R2接收端测量声压；θ为超声波扩散角。

由式(3)、式(5)和式(12)，分别得到不同含油率下αint、αsca和αdiff变化如图5(a)所示。可以看出，随着φd的增大，油滴数量增多，油水界面对超声波的散射作用增强，导致αsca增大；而与αsca相比，αint基本保持不变，且αint数值远小于αsca；同时，αdiff呈现非线性变化趋势，表明声束波阵面上声压分布不均匀。忽略超声吸收衰减对总超声衰减的贡献，则式(6)简化为式(14)。

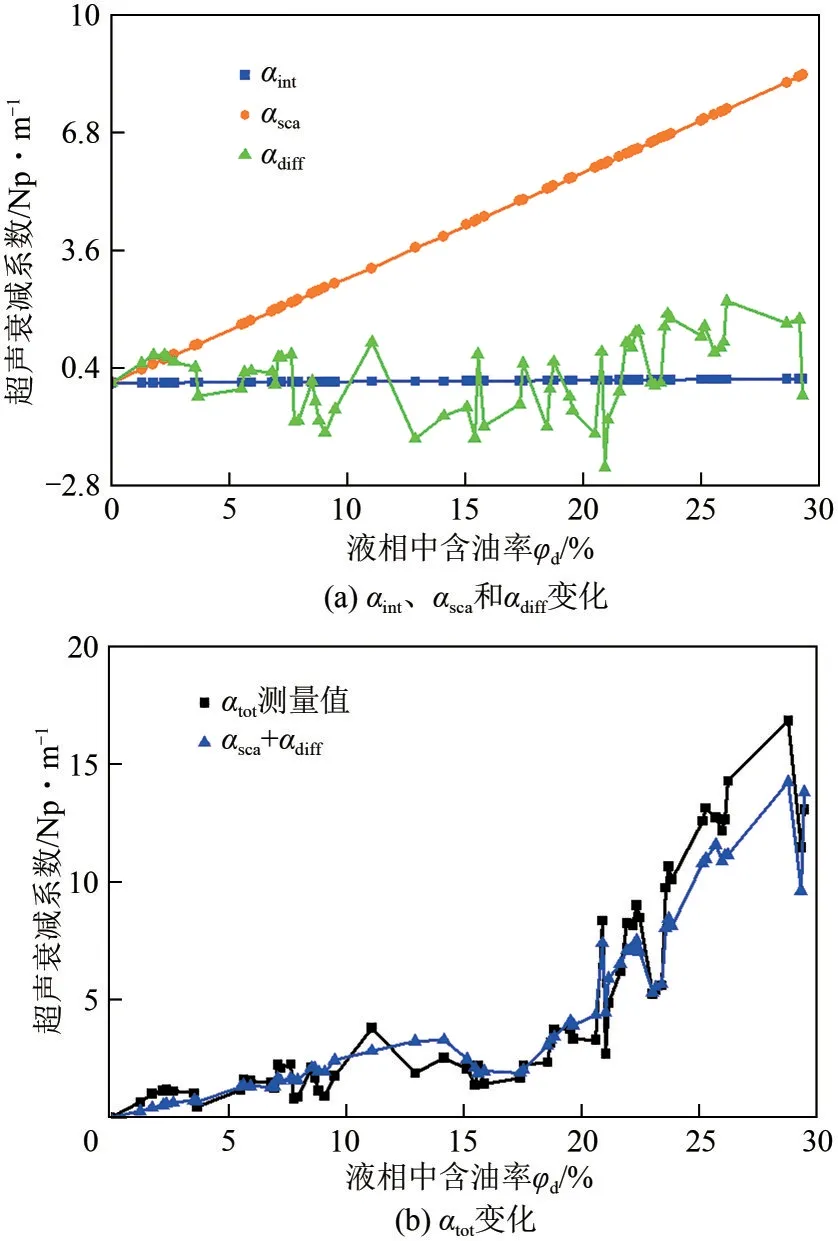
图5 超声衰减系数随含油率变化情况

由式(1)和式(14)，分别得到αtot测量值与理论值如图5(b)所示。可以看出，αtot理论值与预测值变化趋势一致，表明超声波声束的扩散效应是导致总超声衰减测量结果非线性变化的主要因素。

根据上述分析，推导得到水基分散分层流液相中含油率预测模型为式(15)。

式中，pref表示液相为纯水时T/R接收端测量的参考声压。

4.2 油水两相流混合声速优化

声速与流体的密度和可压缩性有关。由表1计算可知，相同温度下，油、水两相声阻抗相差不大，考虑到流体黏度和颗粒尺寸的影响，油水混合物中声速和分散相含率的关系由Urick 模型给出，如式(16)[27-28]。

其中，δ=(2μs/ρcω)1/2为连续相黏性边界层厚度。

Urick 模型忽略了声波散射对声速的影响，为量化油水分散流中油滴散射行为对超声波传播路径的影响程度，由超声波传播理论可知，超声波渡越时间测量结果反映了超声波传播路径变化，通过综合分析多个超声换能器测量的渡越时间信息，定义声程波动参数为式(20)。

式中，K为声程波动参数；t0、t1和t2分别为T/R、R1和R2测量的超声波渡越时间。

如图6所示，对K作初值化变换处理，分析变换后K随含油率变化趋势可知，油滴对超声波多重散射作用具有随机性。从图6还可以看出，当液相中含油率较小时（φd＜16%），K值基本小于1；而随着含油率的增大（φd＞16%），K值总体大于1，这可能是由于与超声波在纯水中传播时相比，油水界面的散射效应对超声波声束产生了一定的汇聚（K＜1）和发散（K＞1）作用。根据上述分析，在Urick模型基础上，将K作为修正参数引入混合声速模型即式(16)，则油水分散流中修正后的混合声速模型为式(21)。

图6 声程波动参数随含油率变化情况

4.3 相含率预测结果与分析

根据脉冲回波测试原理，由超声波渡越时间得到水基分散分层流气液界面高度，则水基分散分层流含气率和含油率测试模型分别为式(22)、式(23)。

式中，φg和φo分别为含气率和含油率。

含气率预测效果如图7，可以看出，当含油率较低时，优化前含气率测试模型预测误差基本分布在±1.6%以内，随着含油率升高，其预测最大误差超过6%；而优化后含气率测试模型预测误差均分布在±1.1%以内。

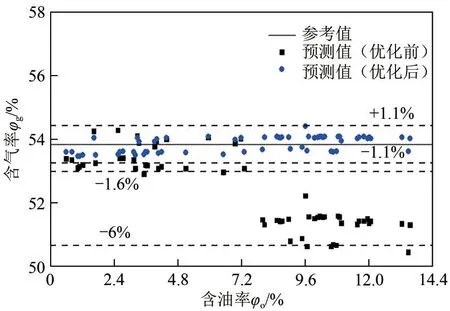
图7 含气率预测效果对比

分别采用Faran模型与ECAH模型预测含油率，含油率预测效果对比及误差分布分别如图8(a)和(b)。可以看出，ECAH模型整体低估了含油率，这可能是由于ECAH模型适用于估计长波长条件下超声能量的热损失和黏性损失，而Faran 模型则更多考虑了中波长条件下超声散射衰减的贡献，且采用Faran 模型得到的含油率预测误差大多分布于±5%以内，表明了所提出超声衰减优化模型的可行性。

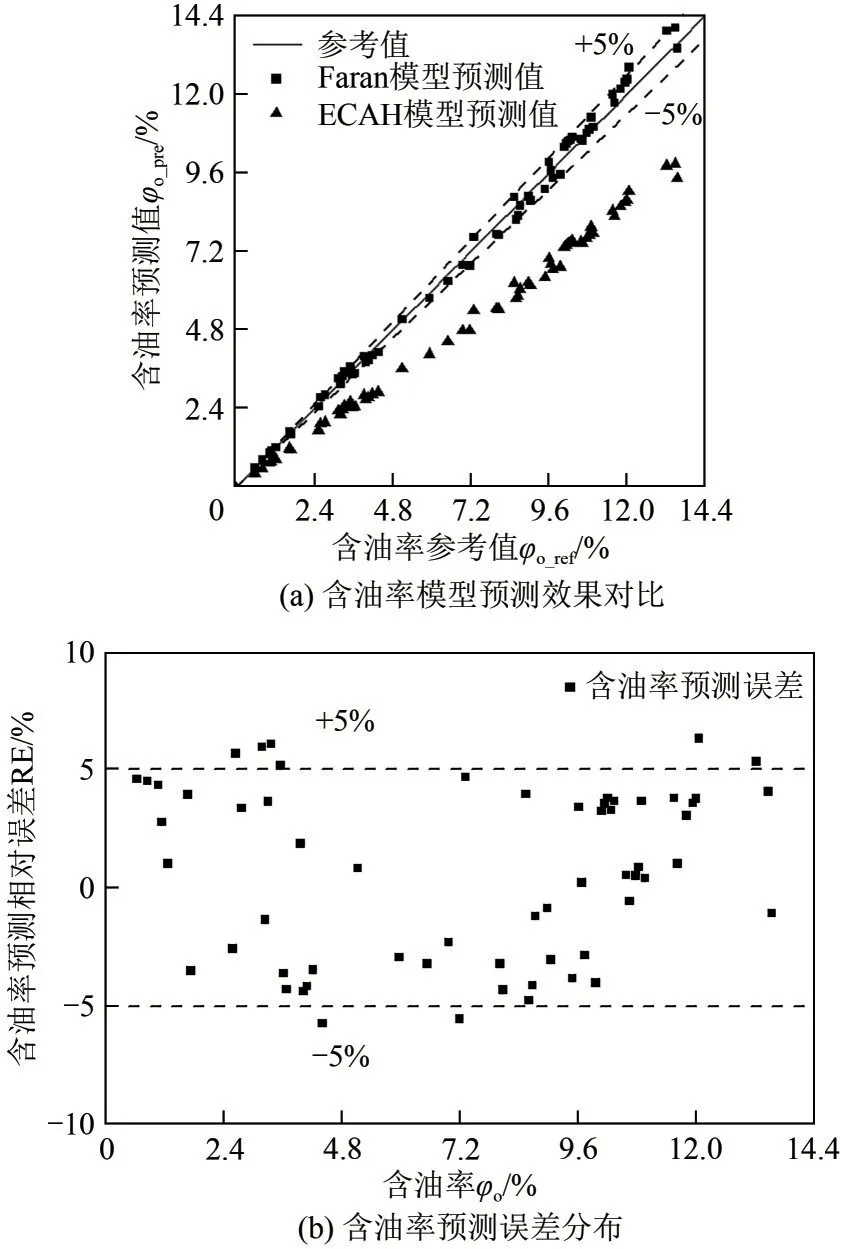
图8 含油率预测效果

为进一步验证所提出水基分散分层流相含率超声测试模型的有效性，分别采用统计指标平均相对误差MRE 和均方根误差RMSE 评价相含率预测效果，见式(24)、式(25)。

式中，N为样本总数。

由式(24)和式(25)得到含气率预测MRE 和RMSE 分别为0.43%和0.24%，含油率预测MRE 和RMSE 分别为3.30%和0.28%，表明优化后的相含率测试模型预测效果较好。

所提出的基于超声方法的水基分散分层流相含率优化模型具有一定预测精度，然而，相含率预测结果仍存在误差，主要包括以下方面：

（1）超声测试仿真模型中，采用“一发三收”测量策略接收气液界面反射回波，然而仍有一些超声回波信号不能被超声换能器接收到，因此该方法可能无法准确获取声束波阵面上声压的切向分布情况，导致超声扩散衰减估计的不确定性；

（2）基于分散相颗粒单散射效应，采用Faran弹性散射模型描述了中波长区超声散射衰减与分散相含率的关系，然而当分散相浓度较高时，可能发生颗粒间的相互作用，影响超声散射衰减模型的适用性；

（3）根据Urick 模型预测油水分散流声速时，采用油、水两相体积分数加权平均方法，计算了油水分散流的有效密度和有效绝热压缩系数，然而水基分散分层流中油滴半径与超声波波长相近，此时将油水分散流视作均质流体，可能无法准确表征油水分散流的声学特性，导致油水分散流中混合声速预测误差。

5 结论

针对水基分散分层流相含率的超声测试问题，提出了一种基于混合声速修正的相含率测试优化模型。

（1）采用Brauner 最大粒径模型，在不同水相表观流速工况下，通过求解油气水三相动量守恒方程，得到了量纲为1波数变化范围为1.035～4.649。

（2）基于单分散颗粒尺寸分布假设，提出了超声扩散衰减估计方法，表明总超声衰减的非线性变化受扩散衰减机制影响；结合Faran 弹性散射理论，建立了水基分散分层流含油率超声测试模型，结果表明，含油率预测MRE和RMSE分别为3.30%和0.28%。

（3）利用超声渡越时间测量信息，建立了声程波动修正参数，通过改进油水分散流混合声速模型，进一步优化了含气率超声测试模型，结果表明，含气率预测MRE和RMSE分别为0.43%和0.24%。

综上，本文基于有限元方法，建立了水基分散分层流超声测试仿真模型，根据超声扩散衰减和散射衰减机理，优化了水基分散分层流相含率超声测试模型，为油气水多相流相含率超声测试方法提供了理论依据。在此基础上，深入探究气液界面高度与粒径变化对相含率超声测试模型的影响是未来研究方向。

符号说明

A——超声波脉冲激励信号幅值，V

a——超声换能器半径，m

B——流体绝热压缩系数，m2/N

CH——Brauner H最大粒径模型中可调常数

c——超声波纵波波速，m/s

cp，cv——分别为流体定压比热容和定容比热容，J/(kg·K)

D——管道内径，m

d——分散相有效直径，m

E——声强比

F——Fanning摩擦因子

f——超声波频率，Hz

g——超声波脉冲激励信号函数

h——气液界面高度，m

K——声程波动参数，混合声速模型中修正参数

k——超声波波数，m-1

l——超声波传播路径长度，m

N——仿真所用样本总数

p——声压，Pa

R——分散相颗粒半径，m

t——时间，s

u——流体速度，m/s

α——超声波衰减系数，Np/m

δ——黏性边界层厚度，m

η——流体纵向黏度，Pa·s

θ——超声波声束扩散角，(°)

κ——热导率，W/(m·K)

λ——超声波纵波波长，m

μb,μs——分别为流体体积黏度和剪切黏度，Pa·s

ρ——流体密度，kg/m3

σ——油水界面张力，N/m

φ——相含率，%

下角标

c, d ——分别为连续相、分散相

diff, int, sca——分别为扩散、吸收、散射

pre, ref ——分别为预测值、参考值