基于环形电导传感器的气液两相流流型识别与过程参数测量

史雪薇，谭超，董峰

（天津大学电气自动化与信息工程学院，天津市过程检测与控制重点实验室，天津 300072）

油气水多相流是一种复杂的流动现象，广泛存在于能源、动力、石油等诸多工业生产过程中[1-2]。近年来随着我国气田开发的跨越式发展，对气液两相流流动过程机理的阐释以及对其流动参数的准确测量逐渐成为科研和工程领域的研究热点问题[3]。发展高精度、高可靠性的多相流检测技术，在线准确获取流动过程信息，对于推动相关科学研究的深入发展及保证工业生产过程的安全性、经济性、高效性具有重要意义。然而与单相流相比，可压缩的气相使得气液两相流具有组成结构复杂、非均匀、非平稳、状态快速变化等特点，为流动参数的测量带来巨大挑战。

管道中多相流呈现的几何动力特征各异的流动形态称为流型。流型不仅对流体的压力降和传质传热性能产生影响，而且多相流流动参数的测量及相关机理模型的建立往往依赖于对流型的充分了解[4]。因此，流型的准确判断和预测对于提高流动参数测量的准确性具有重要意义。由于流型易受管径、管壁粗糙度、流动介质的物理性质、管道的倾斜角度、分相流量等诸多因素影响，研究学者们在不同实验条件下观察到的流型也不同[5-6]。为实现流型的准确识别，国内外众多研究学者在利用传感器技术获取流体流动的过程信息的基础上，开发出各种信号处理方法用于流动特点的有效表征及流型的分类，例如数字图像处理、时频分解、熵分析、复杂网络、神经网络等方法[7-8]。其中，特征提取是流型识别中的难点之一，有效的特征要求能够与流动结构具有较好的关联性。提取与其相关的特征参数将具有更明确的物理意义，有助于提高识别精度和识别结果的可解释性。多传感器融合策略的提出为多相流流型的高效表征提供了一种解决方案[9-10]，但传感器数目的增多大大增加了测量系统的复杂性及应用成本。此外，由于多相流实验过程的复杂性增加了获取分类样本的难度，寻找适用于小样本的模式识别方法逐渐成为人们的研究目标。

流速和含率是多相流中反映流体动力学特性及流动结构特点的两个重要过程参数，与各相流量紧密相关。随着科技的不断进步与发展，众多研究者们已经开发出基于不同传感技术的过程参数测量方法，如快关阀法、光学法、电学法、超声法、射线法、微波法等[11-15]。在众多传感技术中，电导法利用被测流体的电学属性（电导率）实现参数测量，具有测量响应快、安全无辐射、成本低、可测非透明流体、对流体无干扰等诸多优势。因其要求被测流体的连续相为导电相，该方法在以水为连续相的多相流测量中具有十分广泛的应用[10]。根据不同的测量目的，不同形状的电导传感器已被提出，例如平板式电极[16]、弧状电极[17]、环形电极[18]、平面阵列式电极[19]等。其中环形电极可产生较为均匀的电场且具有传感器结构简单、测量模型简单等优势，Shi 等[14]指出当不注重传感器的空间分辨率时，环形电极更适合实际应用。Lucas 等[20]、Devia 等[21]和Jin 等[12]分别针对不同数目的环形电极结构进行了优化，并构建了相应的流动参数测量模型，实现了特定流体的相含率或轴向速度信息的获取。

本文作者课题组利用四环电导传感器，围绕水平管道油气水多相流的流型识别和流速、含率的测量问题开展了系统研究。Wu 等[22]和Fu 等[23]利用电导、电容的测量敏感特性差异，设计了四环电导和对极板电容组合式传感器，并提出了无需流型识别的油水两相流全含率测量方法。Tan等[24]、Liu等[25]和Shi 等[26-27]针对油气水多相流的分相表观测量问题，将四环电导传感器与超声多普勒传感器相结合，分别用于获取流体的含水率及离散相真实流速信息，并通过对特定流型的受力及动量平衡分析构建参数模型以融合多模态测试信息并实现分相表观流速的求解。但是相关研究重点围绕油水两相流展开，且环形电导传感器仅用于提供表观流速测量所必要的含水率信息，尚未考察其在不同流型下的含率测量特性。针对气水两相流的流型识别问题，Fu等[28]、Zhao等[29]利用四环电导传感器获取流动过程参数并从中提取统计或非线性特征，实现了泡状流、塞状流、弹状流3种流型的划分；Dong等[30]通过改进的经验小波变换和等距特征映射对从四环电导传感器获取的含水率数据进行多域波动特征提取和降维处理，实现了泡状流、塞状流、弹状流、波状流4 种流型的准确识别；Sun 等[31]将四环电导传感器和超声传感器相结合以增加流动信息获取的多样性，实现了气水两相流6种流型的准确识别，但多模态传感器的使用增加了测试难度和成本。本文作者课题组的前期研究已经表明：根据不同流型的具体流动特性建立与之相适应的测量模型是提高过程参数测量精度的重要手段，流型的准确辨识是流动过程参数准确测量的必要前提。但是由于多相流的复杂性，同时实现流型的准确辨识和过程参数的准确测量往往需依赖于多模态传感器，目前尚缺乏一种仅利用单一模态传感器的简单、高效、低成本的解决方案。

因此，本文针对水平管道气液两相流，利用六环电导传感器提出一种同时实现流型准确辨识与过程参数准确测量的综合性测试方法。首先，利用六环电导传感器获取被测流体的含水率时间序列及互相关速度信息，并基于信号响应分析，考察含率和速度的波动信息对流动结构的物理反映；进而提取了具有明确物理意义的统计特征，结合支持向量机方法实现了水平气液两相流中泡状流、塞状流、弹状流、分层流、波状流、环状流6种流型的准确划分；最终，根据流型识别结果，构建了不同流型下的分相含率和平均流速的测量模型，并完成了动态实验验证。

1 传感器结构与测量原理

1.1 含水率测量原理

电导法基于电阻测量传感器，要求测量对象是以导电介质为连续相的混合物。本研究采用环形电导传感器结构如图1所示。六个环形金属电极以一定间距镶嵌于管道内壁，与流体直接接触。其中E1和E2为激励电极对，M2和M3为含率测量电极对，M1 和M2 构成相关速度测量的上游传感器，M3和M4构成相关速度测量的下游传感器。各个环形电极之间的间距经过优化设计，分别为1D、0.4D、1.2D、0.4D、1D（D为管道直径）[32]。所用环形电导传感器采用电流激励、电压测量的工作方式。通过向电极E1 中通入交变电流（采用频率为20kHz的正弦波，以减小电极腐蚀，并确保被测流体的电学行为基本上呈电阻性），同时将电极E2接地，可在激励电极对之间形成电学测量敏感场；此时，若测量敏感场内被测流体的体积含率发生变化，混合流体的混合电导率将随之发生变化，进而引起M1与M2、M2与M3、M3与M4之间电势差的改变。因此，通过对流体混合电导率和体积含率之间的关系进行建模，则可由环间输出电压推导出体积含率[21,33]。

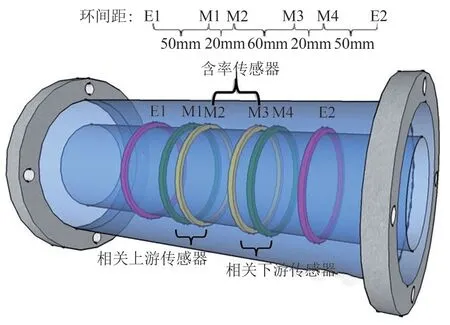
图1 环形电导传感器结构示意图

在含水率测量时，为消除水电导率的影响，一般对M2和M3之间的电势差进行量纲为1化[式(1)]。

式中，V*为量纲为1 电压；V23_w与V23_meas分别为管道内充满水时和管道内充满待测流体时电极M2与电极M3之间的电势差，V。

可利用V*对含水率αw（%）进行测量[式(2)]。

式中，a、b为与流型相关的常数。

1.2 互相关速度测量原理

相关测量技术是在信息论和随机过程相关理论的基础上发展而来的，通过测量流动噪声从上游传感器传到下游传感器时所用的渡越时间，进而得到流体的速度信息。如图1所示，当被测流体在管道内稳定流动时，分别从电导环上游传感器和下游传感器中获取与流动状态相关的电势差波动信号V12(t)和V34(t)。V12(t)和V34(t)分别为电极M1 与电极M2之间、电极M3与电极M4之间的电势差。基于流体流动的“凝固”假设，被测流体在上游传感器引发的测量电压调制，过一段时间后会在下游传感器再次出现并出现相似的信号调制作用。通过对V12(t)和V34(t)进行互相关计算可得到互相关函数[式(3)]。

式中，Rup-down(τ) 为互相关函数；V12(t)和V34(t)分别表示管道中充满待测流体时电极M1、M2和电极M3、M4之间的电势差时间序列，V；τ为流体从上游传感器流向下游传感器的延迟时间，s。Beck等[34]将该迟延时间定义为渡越时间，对应于互相关函数的峰值位置。因此，互相关速度可表示为式(4)。

式中，L为上游传感器与下游传感器的中心距离，m；ucc为互相关速度，m/s，通常被认为是混合流体的结构传播速度。根据漂移模型，互相关速度又可表示为式(5)。

式中，udj为漂移速度，m/s；C为分布参数；um为混合流体的平均流速，m/s。

对式(5)进行形式变换可得式(6)，即混合流体的平均流速可由互相关速度得到。

式中，c、d为与流型相关的系数，可通过拟合获得。

2 气液两相流实验

2.1 实验装置与测量系统

水平管道气液两相流实验在如图2所示的实验装置上完成。水平流体输送管道由内径为50mm、长度为16.6m的不锈钢管组成。电导传感器安装于距离多相流入口约13m的测试管段，以便流型充分发展，每一流动状态下持续测量的时间为10s。同时，在测试管段上设有压力计和温度计用于记录工况条件，高速摄像机用于观察记录流型。实验中所用液体介质为自来水（密度998kg/m3，动力黏度1.01×10-3Pa·s）和干燥空气（密度1.2kg/m3，动力黏度1.81×10-5Pa·s），各相通过一个混合器实现混合，在多相流混合之前通过标准单相流量计对各相流量进行计量，计量误差在1%以内。在出口处，气相被排出，水相直接存储于水罐中以供实验重复利用。实验温度约为20℃。

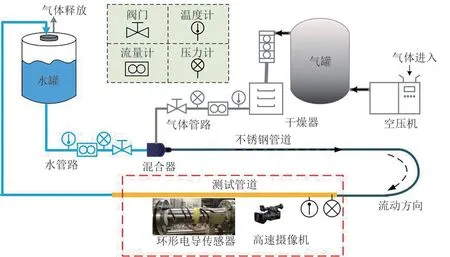
图2 实验装置示意图

实验共分为14组，每组中固定水相流量，逐渐增加气相流量形成不同流型。实验中液体流量范围为0.29～15.00m3/h，标准状况下气体流量范围为1.31～269.79m3/h，总表观流速范围为0.16～25.32m/s。基于Mandhance流型图[35]边界的实验条件如图3所示，图中Jg和Jw分别为气相和液相的表观速度。实验中观察到泡状流、分层流、波状流、塞状流、弹状流、环状流6种流型。

图3 基于Mandhance流型图的实验条件

为实现准确、可靠地获取不同流型下的环间电压，基于紧凑型外设部件互联标准总线（compact peripheral component interconnect, CPCI）开发了电导传感器测量系统。如图4 所示，该测量系统以现场可编程逻辑门阵列（field-programmable gate array, FPGA）为核心，通过编程可控制外围电路实现激励信号产生、数据预处理、高速模数转换、数字解调与CPCI 数据传输等功能[26]。激励信号产生模块采用FPGA 控制AD9754 芯片通过直接数字信号合成（direct digital synthesizer, DDS）技术产生频率可调的交变电压信号，经过带通滤波、放大、跟随后利用压控流源（voltage controlled current source, VCCS）电路将电压信号转为电流信号并最终施加到激励电极对上。测量电极对上的环间电压经过阻抗匹配、电压跟随、低通滤波、可编程放大及高速模数转换等数据处理后在FPGA内部进行数字解调，获得被测物场内的介质分布信息。最后采用专用接口芯片PCI9054 实现CPCI总线与本地总线的桥接，采用工业控制总线机箱的J1 接口将测量数据上传至上位机（最高可达到32bit/33MHz 的传输速率）以实现数据的采集、存储及后续处理。

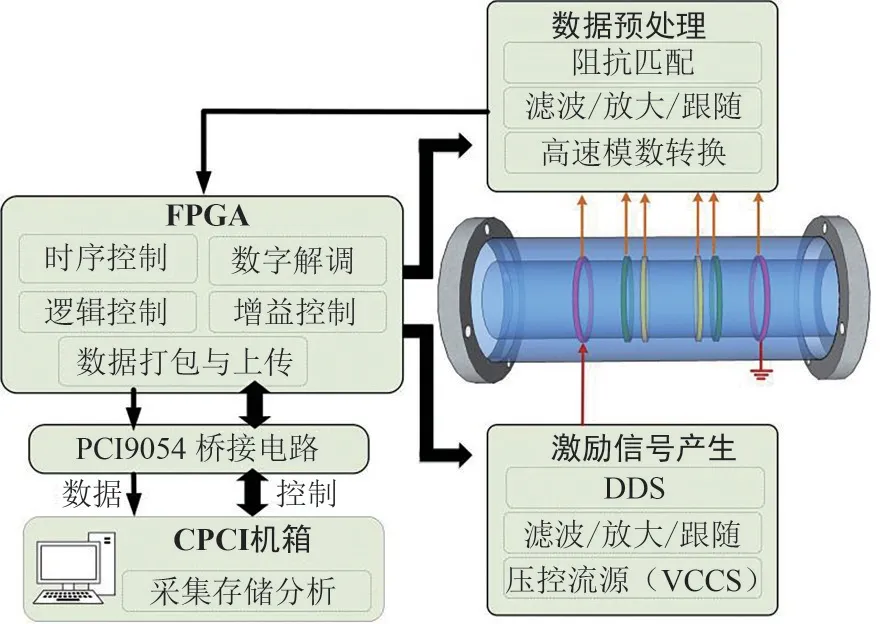
图4 测量系统结构

2.2 实验观察与流动特性

图5为高速摄像机捕捉到的不同流型下的流动图片。分层流通常发生在气流量和液流量较低时，在该流型下气液两相由于其密度差异，以分层的形式平稳流动，其中较重的液相沿着管道底部流动，而较轻的气相沿着管道顶部流动，如图5(a)所示。在分层流的基础上增加气相流量，气液界面上会出现明显的波动，形成波状流，如图5(b)所示。若继续增加气相流量，液相则形成一层薄膜包裹管壁流动且管道底部液膜厚度常大于管道顶部液膜厚度，气相以气核的形式沿着管道中心流动且气核中常夹杂由液膜表面撕裂形成的细小水滴，此时形成环状流，如图5(c)所示。泡状流通常发生在液相流量较高而气相流量较低的情况，在该流型下大量离散气泡混杂在液相当中，气泡尺寸较小，且主要聚集在管道中上部，如图5(d)所示。当液相流量处于中等水平而气流量较低时会形成塞状流，此时连续流动的液相携带由长气泡形成的气塞和细小气泡一起流动，如图5(e)所示。若在塞状流基础上增加气相流量，气相则形成尺寸较大的气弹，并与液弹交替在管道中流动，形成弹状流，如图5(f)所示。弹状流的流动具有明显的间歇特性且气相和液相之间存在强烈的相互作用，容易对管道安全造成威胁。

3 流型识别

3.1 信号响应

多相流流动参数的准确测量往往需要根据不同流动对象及流型的特点采用特定的测量模型。因此，流型的准确识别是提高流动参数测量的准确性的前提和基础。将含率测量电极对上的测量电压利用式(1)进行处理得到不同流型下的量纲为1电压波动时间序列。由式(2)可知，量纲为1电压与含水率成正比，可直接反映含水率的波动情况。

如图6 所示，不同流型下的量纲为1 电压时间序列具有不同的波动形式。对于分层流，因其流动较为平稳，其量纲为1电压时间序列呈现较为平缓的大尺度波动。而波状流中气液界面的波动往往包含较大幅度的滚波和较小幅度的纹波，进而造成含水率的不同波动，因此其量纲为1电压时间序列的波动表现为由大幅波动与小幅波动共同组成。在环状流中，因液相以薄液膜的形式附着在管道内壁，其含水率较低；此外气液之间强烈的相互作用使得液膜的波动性明显增加，甚至造成气相中的液滴夹带，造成其量纲为1电压时间序列表现为在较小的水平上叠加高频波动的形式。对于含水率较高的泡状流，其含水率的波动主要由于分散在水中且尺寸较小的离散气泡引起，因此该流型下的量纲为1电压波形主要在较大水平上呈现小幅高频波动的形式。塞状流中，细长的气塞与小气泡共同伴随水相一起流动，气塞的间断出现使得含水率突然下降，因此量纲为1电压时间序列呈现偶发的低频大幅度波动形式。弹状流中，较大尺寸的气弹所引起的含水率波动幅度大大增加，且由于气弹与液弹交替出现的间歇特性使其含水率波动呈现一定的周期性，在气弹经过时含水率出现低谷，在液弹经过含水率出现高峰。

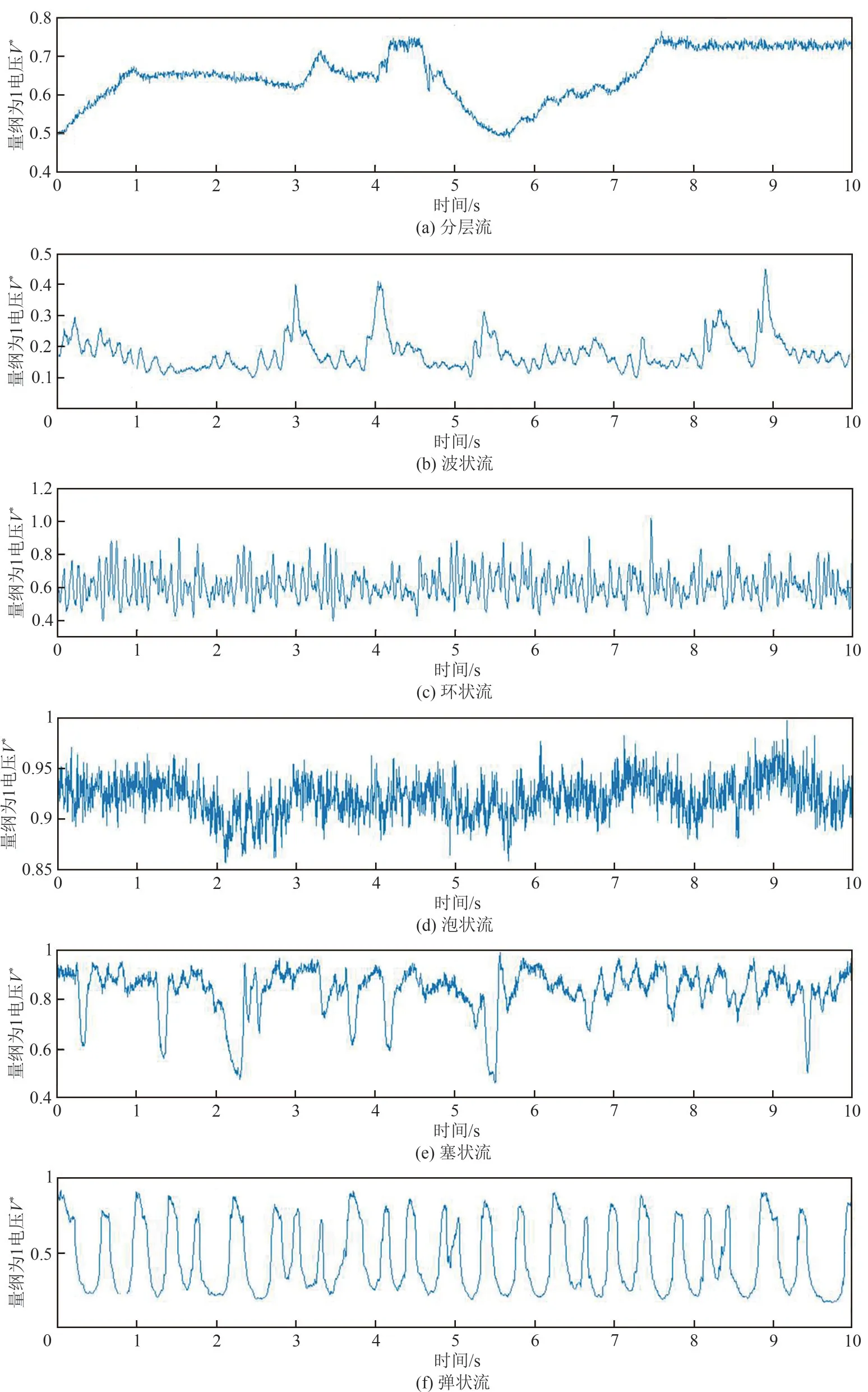
图6 不同流型下的量纲为1电压波动时间序列

图7所示为不同流型下上下游互相关传感器所获取的电压波动序列。从图中可以看出，在不同流型下，下游电压波动序列V34与上游电压波动序列V12之间存在良好的相似性，只是在时间上滞后一段时间。通过对上下游电压波动序列进行互相关计算，得到不同流型下的互相关函数如图8所示。可以看出，不同流型下互相关函数的峰值位置不同。由于互相关函数峰值所对应的时间为渡越时间，它指示了流体从上游传感器流向下游传感器的延迟时间，由式(4)可计算得到两相流的互相关速度。

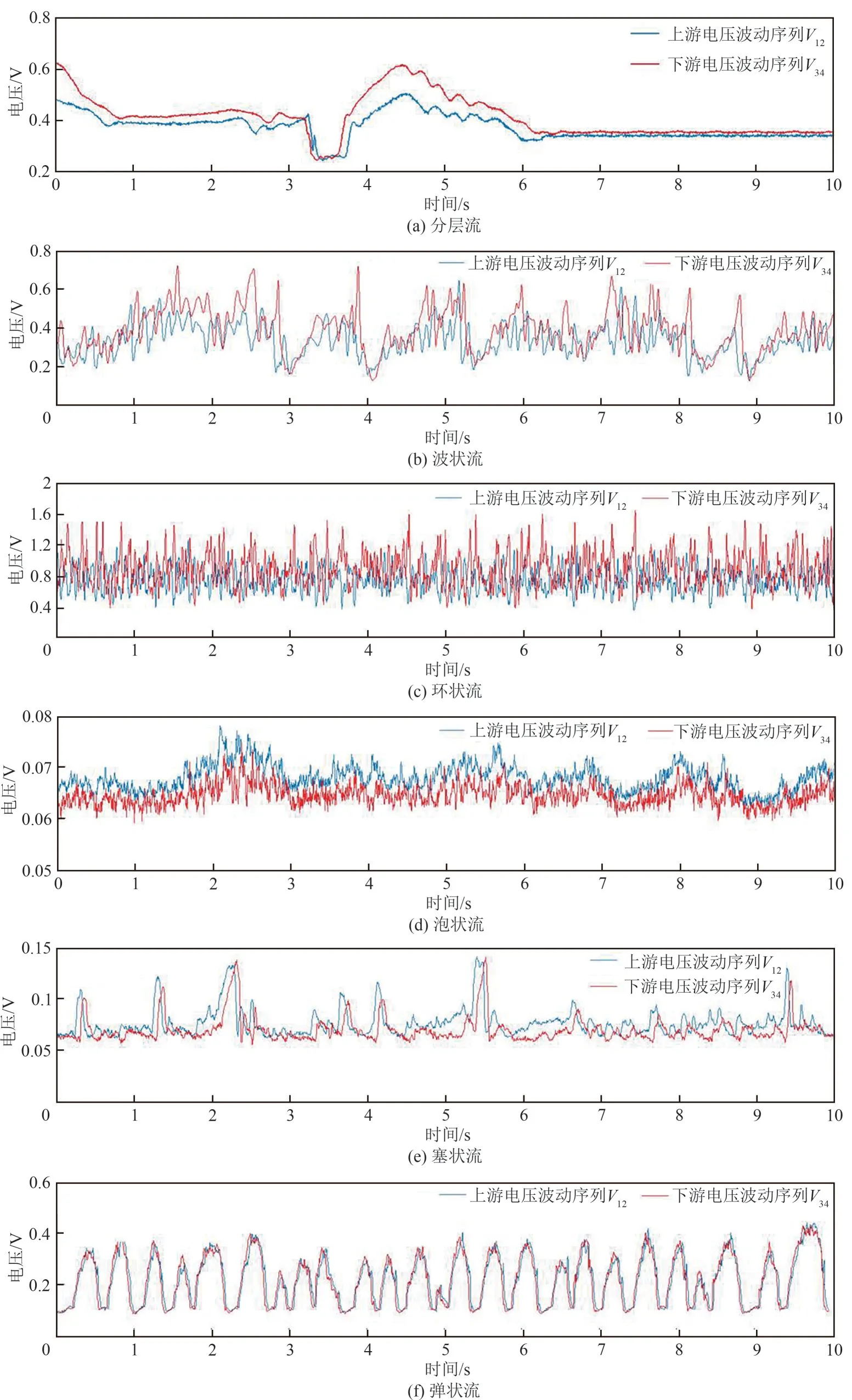
图7 不同流型下互相关传感器上下游电压波动时间序列

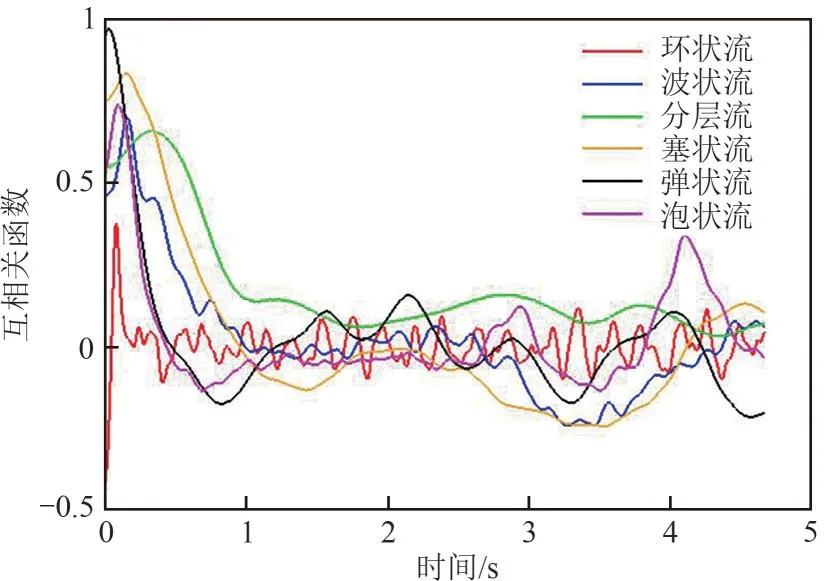
图8 不同流型下的互相关函数

3.2 特征提取

基于以上分析，不同流型下的量纲为1电压时间序列具有不同的波动特性，上下游互相关传感器所获得的电压波动序列的互相关函数具有不同的峰值位置。因此计算量纲为1电压时间序列的均值-V*[式(7)]和方差σV*[式(8)]。

式中，M为序列的总长度。

二者与互相关速度一起组成特征向量S作为流型识别的统计指标[式(9)]。

以上统计指标直接与含率和流速相关，进而与流型相关，且具有较为明确的物理意义：量纲为1电压均值与含水率成正比，可表征某流型下气液两相的流量比；量纲为1电压方差表征某流型下流动结构的波动情况；互相关速度表征某流型下速度的大小。

3.3 流型识别

支持向量机（support vector machine, SVM）是Corinna Cortes 和Vapnik 等在1995 年首次提出的一种有监督的机器学习方法，它在解决小样本、非线性及高维模式识别及回归分析中表现出许多特有的优势[36]。虽SVM 本质上为二分类器，但可通过“一对多”和“一对一”策略解决多分类问题。针对水平气液两相流的流型识别这一典型的多分类问题，采用“一对一”策略实现不同流型之间的划分，即训练时对任意两类流型样本均训练一个二分类器，则6 种流型下共可得到15 个二分类器。对未知样本的类别进行预测时，使用所有的二分类器进行分类，将出现最多的那个类别作为该样本的最终分类结果。为验证特征向量S对流型划分的准确率，将全部样本分成两部分，分别用于SVM 的训练和测试，其中核函数选取径向基核函数，采用交叉验证的方法对模型参数进行优化（得到径向基核函数参数gamma=0.87，惩罚因子=147.03）。将测试结果与高速摄像机的观察结果作对比，计算识别准确率，结果如图9 所示。每种流型的样本总数、训练样本数、测试样本数和流型识别结果如表1 所示。从表1 中可知，所提出的方法可实现水平管道气水两相流中分层流、波状流、泡状流、塞状流、弹状流和环状流的准确划分，平均识别率为93.1%。

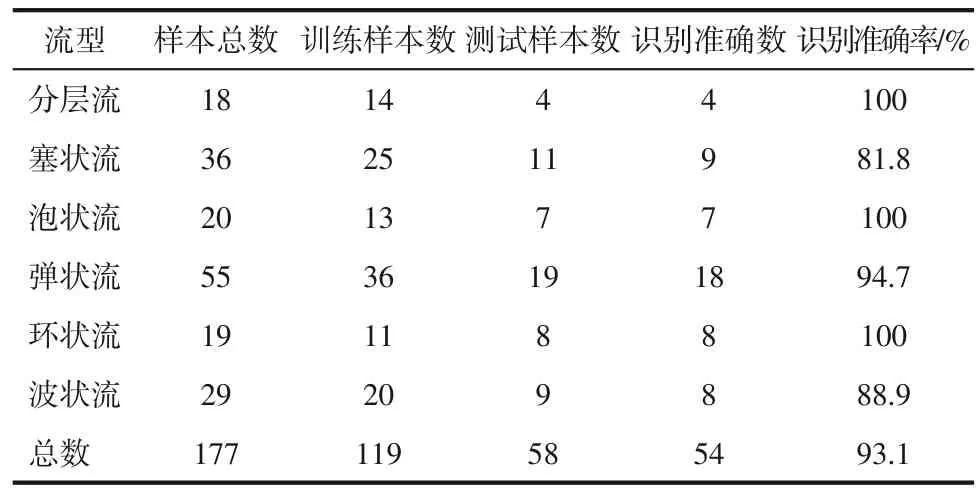
表1 不同流型下样本数及识别结果

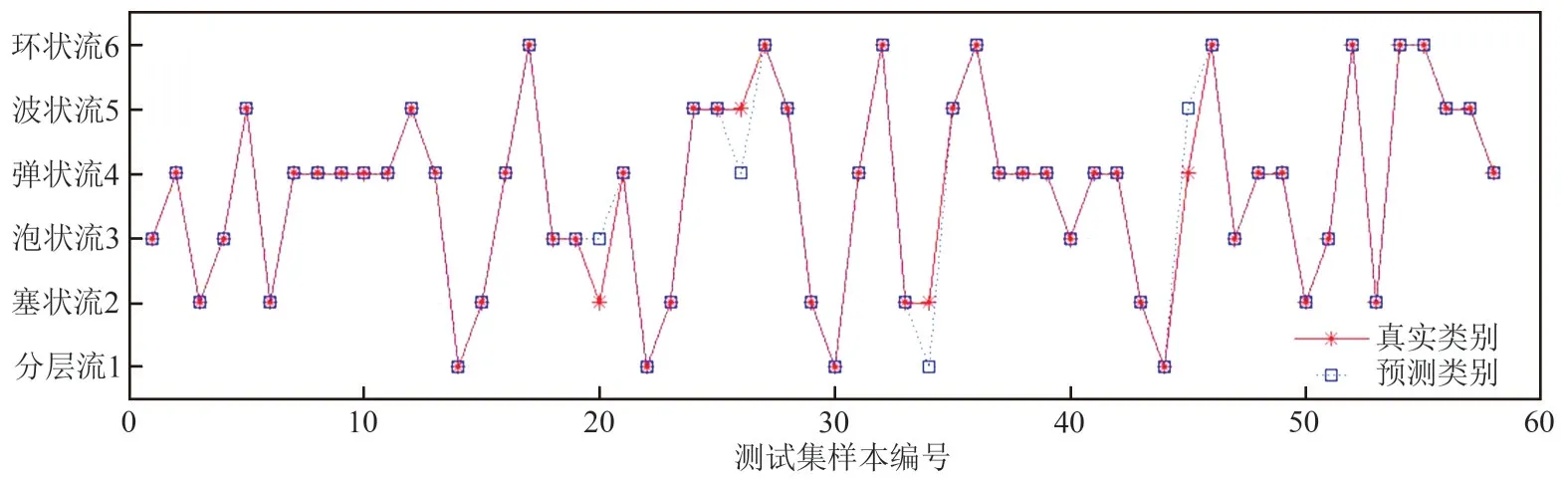
图9 测试集SVM预测结果

4 过程参数测量

4.1 分相含率测量

为实现含水率的准确计算，需要确定式(2)中含水率计算模型的基本参数a和b。因此，在流型识别基础上，将量纲为1电压与入口单相流量计计量得到的参考含水率在不同流型下分别进行拟合，得到不同流型下的含水率计算模型的基本参数，拟合结果如图10、式(10)所示。

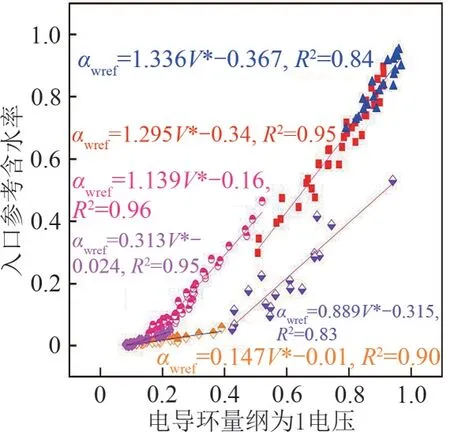
图10 含水率计算模型参数拟合结果

式中，αwref为入口参考含水率（%），且式中的斜率和截距即为含水率计算模型式(2)中的基本参数。进而可利用式(2)进行含水率计算，则含气率αg（%）为式(11)。

将计算得到的含水率和含气率与入口处的参考含率进行对比，并定义均方根误差对结果进行定量评价[式(12)]。

式中，RMSEα为含率的均方根误差；αcal和αref分别为模型计算所得含率和入口参考含率，%；K为总的实验点数。

含水率计算模型参数拟合结果如图11 所示。从图11 中发现，模型计算所得含水率和含气率与入口处参考含率吻合程度较好，均方根误差分别为2.56%和2.73%。

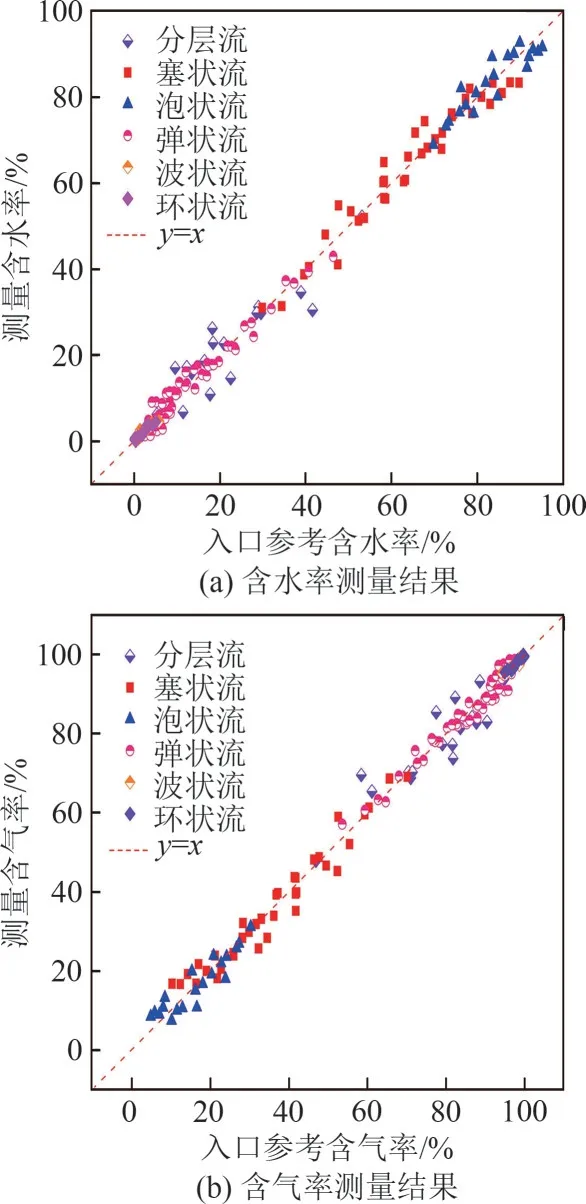
图11 含率测量结果

4.2 速度测量

在流型识别的基础上，将计算所得的互相关流速与由入口处的参考混合流速在不同流型下分别进行拟合，可得到式(6)中混合流体平均流速计算模型的基本参数c和d在不同流型下的取值。需要注意的是，在进行互相关流速计算时，用于相关的上、下游电压时间序列的长度对结果具有重要影响：太长的时间序列将包含过多的流动特征，容易拉平互相关函数的峰值，甚至造成多峰的现象；而包含少量流动特征的短序列则可能导致互相关计算的失败[33]。因此，根据特定的流动条件合理选择相关信号的长度，有助于提高流速计算的准确性。如图12 所示为用于相关计算的上、下游电压时间序列长度为2s、4s、6s、8s、10s 时，所得互相关流速与入口参考流速的拟合结果。由于分层流流动过于平稳，互相关速度计算准确性较低，因此以上拟合不考虑分层流。

图12 不同相关序列长度下平均流速计算模型参数拟合结果

由图12 可知，泡状流和塞状流在序列长度为8s 时拟合优度最好，弹状流在序列长度为4s 时拟合优度最好，波状流和环状流在序列长度为2s 时拟合优度最好。选取各流型拟合优度最好时的拟合结果作为最终的平均流速计算模型见式(13)。

式中，umref为入口参考平均流速，m/s；式中的斜率和截距分别为平均流速计算模型式(6)中的c和d。

利用式(13)所得的模型参数，结合互相关速度可计算得到混合流体的平均流速，并与入口处的参考平均流速进行对比。定义均方根误差对结果进行定量评价[式(14)]。

式中，RMSEu为平均流速的均方根误差；umcal和umref分别为计算所得平均流速和入口参考平均流速，m/s；N为参与计算的实验点个数。

结果如图13 所示，发现模型计算所得平均流速与入口参考流速吻合程度较好，均方根误差为0.69m/s。

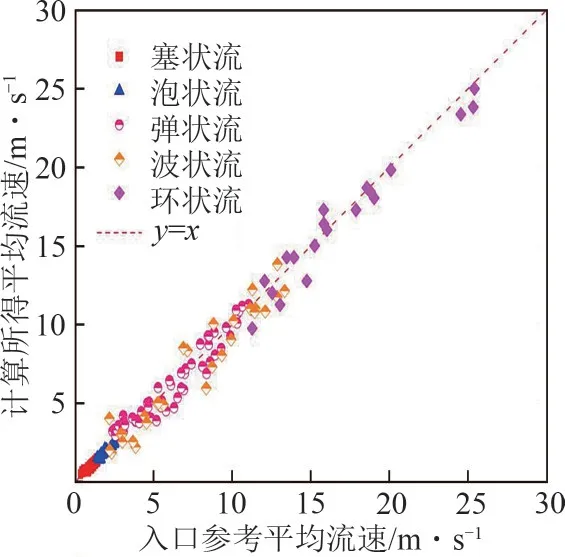
图13 平均流速计算结果

5 结论

多相流过程参数的测量往往需要根据不同流型的特点采用特定的计算模型。因此，本文针对水平管道气液两相流，利用环形电导传感器提出一种同时实现流型准确辨识与过程参数准确测量的综合性测试方法。

（1）首先，利用由六个环形电极组成的电导传感器获取三个不同的环间电势差，并分别建立特定环间电势差与含水率和互相关速度的测量模型；同时，通过分析不同流动状态下环间电势差的变化趋势，考察含率和速度的波动信息对流动结构的物理反映，进而从中提取具有明确物理意义的统计特征对流型进行客观表征；最终，采用适用于小样本的支持向量机方法，以“一对一”策略构建了15 个以径向基为核函数的二分类器实现了泡状流、塞状流、弹状流、分层流、波状流、环状流6种流型的准确划分，平均识别率为93.1%。

（2）根据流型识别结果，针对性地提出利用量纲为1电压和互相关速度获取气液两相流不同流型下分相含率和平均速度的计算模型，并与入口参考含率和流速进行了对比。结果表明：含率计算模型在所有流型下均表现良好，含水率和含气率的均方根误差分别为2.56%和2.73%；平均流速的计算模型在泡状流、塞状流、弹状流、波状流和环状流下表现良好，均方根误差为0.69m/s。而分层流因流动状态过于平稳，无法根据互相关速度获得准确的平均流速计算结果，可通过其他传感模态进行弥补。

（3）所提方法为水平管道气液两相流提供了一种简单、高效、低成本、非侵入性的流型识别和过程参数测量策略，对多相流的工业应用和科学研究具有重要意义。然而，该方法具有一定的局限性：在流型识别方面，利用支持向量机的“一对一”策略实现6种流型的分类时需要的二分类器较多，可采用“一对多”策略减少二分类器的使用，以降低存储开销和训练时间；在参数测量方面，由于不同流型所呈现的流动特性具有较大差异，导致流速和含率测量模型的选取需依赖于流型的识别结果，因此流型的准确识别是提高参数测量精度的必要前提。此外，基于互相关原理的速度测量方法通常要求上、下游电压序列需包含明显的流动状态特征且具有良好的信噪比，过于平稳的流动状态或较大的测量噪声容易导致互相关运算的失败；同时，为了提高测量准确性，上、下游传感器的间距及用于相关运算的信号长度应合理选取。