高碾压混凝土拱坝整体稳定安全评估与工程类比研究

汪 妍，程 恒，杨仕志，解凌飞，杨 波，李 烽

(1.中国水利水电科学研究院，北京 100038；2.湖北省水利水电规划勘测设计院，湖北 武汉 430064)

0 引 言

作为一种超静定结构，拱坝在实际运行过程中难以避免地会出现局部屈服开裂的现象，但只要不发生拱坝-坝基系统的整体破坏，拱坝仍可正常运行[1]，因此，拱坝的整体安全性[2]是工程界重点关注的问题。拱坝整体安全性研究主要包括物理模型和数值模拟两类方法，物理模型即采用地质力学模型试验[3-4]，通过试验直观反映实际的工程地质问题；数学模拟方法已被越来越广泛地应用于拱坝的研究分析，主要包括刚体极限平衡法[5]、拱梁分载法[6]和有限元法[7-8]。如今有限元法已逐渐成为数值模拟的主要方法，针对拱坝整体稳定分析，常用的有限元方法为超载法[9]和强度储备法[10]，通过逐步增加荷载和减小材料强度的手段分析拱坝-坝基系统的极限承载能力，并以收敛性判据、突变性判据和塑性区贯通判据[11]，以此参数评判系统是否达到临界破坏状态。目前已有学者进行了相关研究并将此类研究方法应用于实际拱坝工程的整体安全性分析，如余天堂等[12]采用强度储备法和超载法研究锦屏拱坝在多种工况下的应力场和位移场以及左右岸不利地质构造对拱坝工作性态的影响；杨强等[13-14]根据先前提出的变形加固理论，证明了用结构整体安全度与塑性余能的关系曲线来描述结构整体稳定性的可行性；宁宇等[15]采用了水压力超载法及强度折减法来评价白鹤滩水电站拱坝的整体安全性；程恒等[16]采用强度储备法对五嘎冲拱坝坝肩加固前后坝基岩体及结构面的变形、屈服区进行对比分析，采用水容重超载法分析拱坝坝体和地基岩体的变形以及屈服状态的发展过程。

为此，本文依托国内某高碾压混凝土拱坝，综合模拟主要结构面、岩体材料分区以及坝体结构特征，建立拱坝整体稳定三维有限元模型，利用自主开发的SAPTIS[17-20]有限元软件，采用非线性有限元法对正常运行条件下拱坝-地基的变形、屈服情况进行分析；采用水容重超载法，计算拱坝的极限承载能力，通过工程类比，结合5个安全系数，综合评价该拱坝的整体安全性，为拱坝的安全运行提供依据。

1 计算分析方法与模型

1.1 计算模型

本文研究的高碾压混凝土拱坝为二等大(2)型工程，水库正常蓄水位745.00 m，死水位715.00 m，校核洪水位749.02 m；挡水建筑物为碾压混凝土拱坝，坝顶高程750.0 m，最大坝高175 m，拱冠梁处坝顶宽10 m、坝底宽40 m，是目前世界上待建的最高碾压混凝土双曲拱坝。

根据拱坝揭示的地形地质资料及拱坝结构设计成果，综合模拟坝体、基础岩体中的各控制性的地质边界条件以及基础处理措施，建立拱坝整体稳定三维有限元模型。模型考虑了基础中主要断层、软弱夹层、裂隙、岩体材料分区以及坝体结构特征，有限元网格中共有433 341个节点，716 528个单元。坐标系取为x向为横河向，指向左岸为“+”；y向为顺河向，指向下游为“+”；z向为竖直方向，竖直向上为“+”。有限元计算模型如图1所示。

图1 三维有限元模型示意

1.2 计算方法

本文进行非线性计算时，采用DP屈服准则模拟坝体混凝土与地基岩体的材料非线性，模拟基岩中断层、软弱夹层等地质构造时，采用的节理单元满足Mohr-Coulomb屈服准则(单元厚度按照实际结构面厚度取值)。本文以水容重超载法评价拱坝的整体安全性，通过超载计算确定的超载倍数λ，并以此评价拱坝安全性。

本文对于混凝土和岩石等脆性材料采用Drucker-Prager屈服准则[21]，即

(1)

式中，I1为应力张量第一不变量；J2为偏应力张量第二不变量；a和k为材料参数，与材料摩擦角φ和黏聚力c有关，a和k分别为

(2)

(3)

Mohr-Coulomb屈服准则的屈服条件为

(4)

式中，θσ为应力Lode角。

1.3 计算参数

根据地质所提供资料，坝体为C9025混凝土，弹性模量E=28 GPa，泊松比υ=0.166 7，线膨胀系数α=0.7×10-5/℃，容重ρ=24 kN/m3，黏聚力c=1.5 MPa，摩擦系数f=1.2。坝基工程岩体及结构面的物理力学参数见表1。

表1 坝基工程岩体及结构面的物理力学参数

2 正常运行条件下拱坝-地基整体非线性有限元分析与安全评价

2.1 变形分析

正常运行条件下，具有代表性的荷载组合为正常蓄水位+自重+设计温降+泥沙压力+扬压力(简称正常蓄水位+温降工况)。图2为正常蓄水位+温降工况下坝体-坝基整体变形云图，图3为正常蓄水位+温降工况下大坝顺河向变形云图，其中，横河向变形向右岸为“+”，顺河向变形向下游为“+”。由图2、3可知，在此工况下，拱坝在上游水推力作用下向下游变形，其中拱冠梁坝段坝顶部位向下游变形最大，达到6.94 cm；在拱端对两岸坝肩岩体产生挤压变形，坝肩岩体向河床及下游变形。地基及坝体变形规律和变形量值正常。

图2 坝体-坝基整体变形云图(单位：m)

2.2 屈服状态分析

图4为正常蓄水位+温降工况下结构面的屈服分布情况，棕色为屈服状态。由于岩体与坝体混凝土相比强度较低，在荷载作用下坝基岩体产生了屈服，坝基岩块屈服较小，主要是岩体结构面产生屈服，其中，J322、J323、J324、J325与其他结构面相比，屈服区较大，但主要出现在靠近河谷一定范围；J2、J4优势节理屈服范围较小，L3、F6、F1主要在交叉处屈服较为明显。总体上，坝基屈服区多出现在基础表面，深度较浅，未形成贯通性的屈服区。

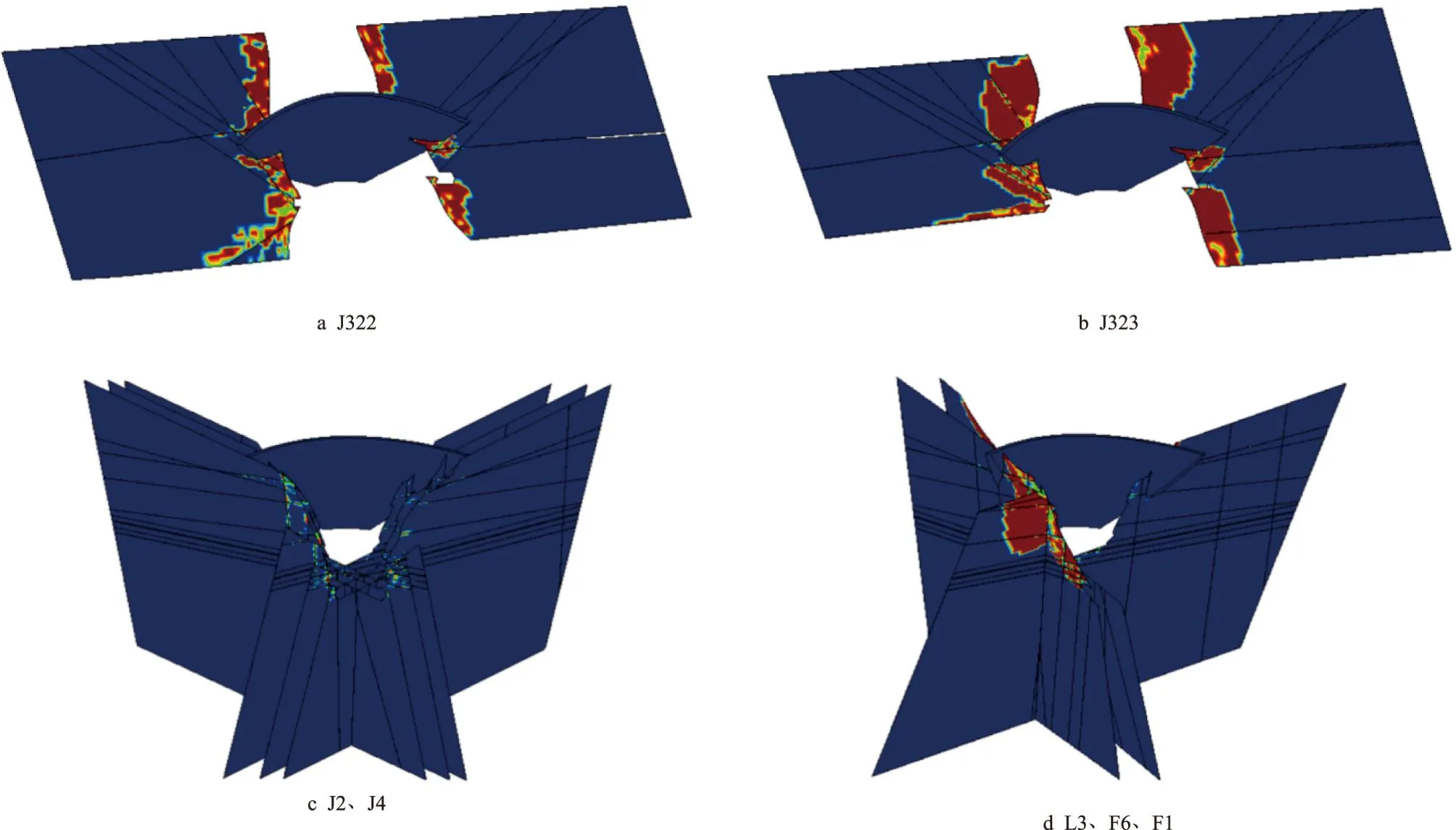
图4 结构面屈服区分布

图5为正常蓄水位+温降工况下坝体的屈服分布情况。坝体上游拱端及坝踵局部出现拉伸屈服，但屈服范围很小，坝体其余部位拉应力未超出混凝土抗拉强度；坝体压应力均小于混凝土抗压强度。

图5 坝体屈服区分布

3 拱坝-地基极限承载能力与安全度分析

根据非线性有限元计算结果，超载计算以正常蓄水位+温降工况为基础，进行水压超载计算。采用水重度超载法，以0.2倍步长进行超载，其他荷载保持不变，计算拱坝的极限承载能力，以此评价拱坝的整体安全性。

3.1 变形分析

图6为拱坝不同部位顺河向变形与超载倍数关系曲线。由图6可知，当超载倍数逐渐增加，坝体各个部位的顺河向变形逐渐增大，坝体中部变形比两岸坝肩变形大，右岸坝肩变形大于左岸；在超载初期，坝体各部位顺河向变形逐渐增大、基本呈匀速发展，超载4.8～5.0倍之后，变形速率明显增加，超载增加至7.2倍时，大坝变形大幅增大，达到极限承载能力，坝体可能存在失稳风险。

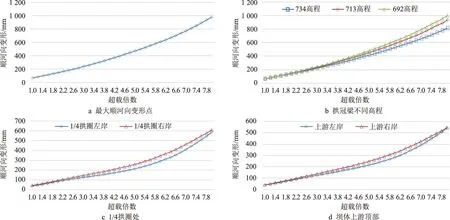
图6 拱坝不同部位顺河向变形与超载倍数关系曲线

3.2 屈服状态分析

图7为坝体拱冠梁剖面屈服情况。由图7可知，结构的大致破坏过程为坝踵部位首先受拉破坏，随着超载倍数的逐渐增大，屈服区逐渐向基岩下部和建基面下游方向扩展；下游坝面中部随后发生屈服，并逐渐向上游方向延伸；一旦屈服区贯通，结构破坏加速。在正常荷载作用时，坝踵及附近基岩出现少量屈服区；在1.6倍超载时，拱冠梁坝段下游面中下部出现少量屈服；在1.8倍超载时，下游面屈服区扩大且坝趾处出现少量屈服区；随着荷载的增大，下游面屈服区向坝体内部不断扩展；至2.6倍超载时，大坝建基面产生了贯通性的屈服区；当超载达到7.2倍时，拱冠梁坝段的坝体与建基面屈服区发生贯通，存在失稳破坏的可能性。

图7 坝体拱冠梁剖面屈服情况

图8为大坝上游面和下游面屈服情况。由图8可知，在1.6倍超载时，坝体下游面中上部出现明显屈服区；在1.8倍超载时，坝体下游下部出现明显屈服区；随着荷载的增大，下游坝面中上部屈服区逐渐向四周扩展，下游坝面底部屈服区逐渐向大坝上部及两侧扩展，当超载达2.2倍时，下游面中上部屈服区与底部屈服区贯通；当超载达5.6倍时，上游坝面大面积屈服；随着超载倍数的增加，左、右坝肩屈服区逐渐向坝体中间及下部扩展；当超载达7.2倍时，上下游坝面绝大部分面积均已屈服。

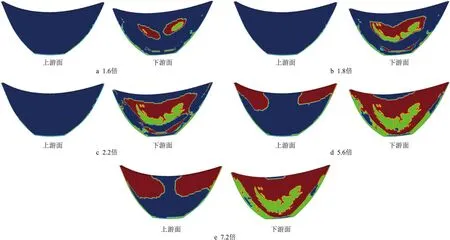
图8 大坝屈服情况

图9为坝体屈服体积比与超载倍数关系曲线。由图9可知，当超载达到1.8倍以上时，坝体屈服量增加速度加快，说明坝体在1.8倍荷载以后坝体下游坝面中部出现较大屈服区，且扩展速度增加迅速。

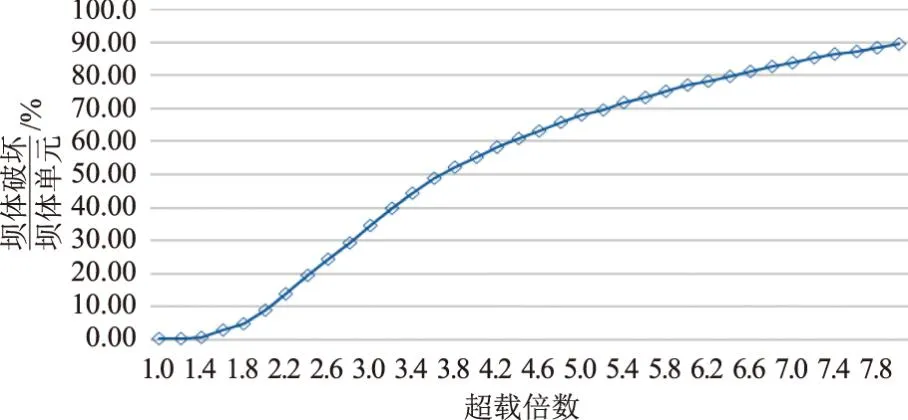
图9 坝体屈服体积比与超载倍数关系曲线

3.3 安全度工程类比分析

本文研究的拱坝以及其他各类比拱坝工程超载安全系数结果见表2。由表2可知，各拱坝的坝踵起裂安全系数λ1基本均在1.0左右；该拱坝达到防渗帷幕的安全系数λ2为1.6，在诸类比工程中位列第3；屈服体积比曲线出现转折的安全系数λ3为1.8，仅次于锦屏、溪洛渡；最大变形曲线出现拐点的安全系数λ4为5.0，仅次于锦屏；最终不收敛安全系数λ5较大，DP准则下可达到7.2，也仅次于锦屏。由于锦屏拱坝的计算材料参数取值偏高，锦屏拱坝的各项安全系数明显偏高。

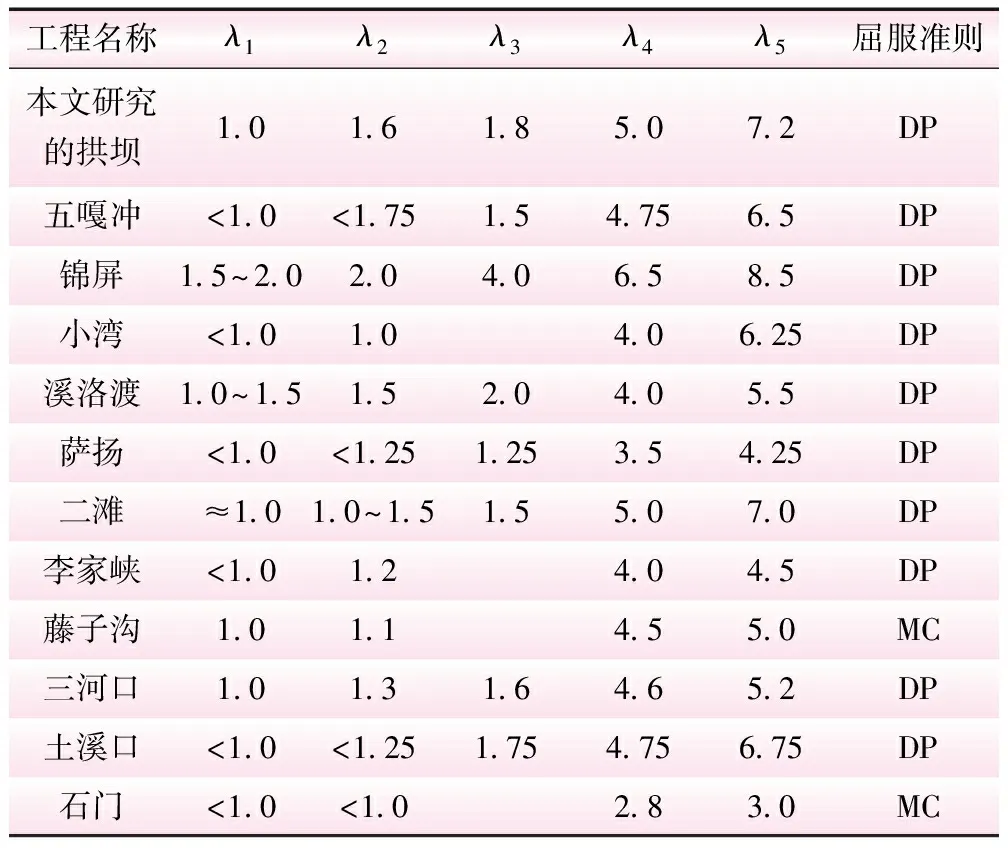
表2 该拱坝及类比工程安全系数[16]

因此，综合5个安全系数，本文研究的拱坝安全系数较高，处于拱坝工程的偏上位置。

4 结 论

本文依托目前世界上待建的最高碾压混凝土双曲拱坝，对正常运行条件(正常蓄水位+温降工况)下拱坝-地基整体进行了非线性有限元分析与安全评价，综合模拟主要断层、软弱夹层、裂隙、岩体材料分区以及坝体结构特征，计算了拱坝-地基的整体工作性态；在此基础上采用水容重超载法，给出了拱坝-地基系统的整体安全度，并通过工程类比综合评价该拱坝的整体安全性，得到以下结论：

(1)正常运行条件下，地基及坝体变形规律和变形量值正常，坝基岩块屈服较小，屈服区多出现在岩体结构面，但未形成贯通性的屈服区。坝体上游拱端及坝踵局部出现拉伸屈服，但屈服范围很小，坝体其余部位拉应力未超出混凝土抗拉强度；坝体的压应力均未超过混凝土抗压强度。整体而言，拱坝整体稳定性较好。

(2)本文研究的拱坝的5个超载安全系数分别为1.0、1.6、1.8、5.0、7.2，经过工程类比，该拱坝安全系数较高，处于拱坝工程的中等偏上水平。