渗流输沙过程的颗粒运动状态和影响因素分析
冯 梅,王 刚,,张甲波,白玉川,黄 哲
(1.河北省海洋地质资源调查中心,河北 秦皇岛 066000;2.河北省海洋岸线生态修复与智慧海洋工程研究中心,河北 秦皇岛 066000;3.天津大学水利工程仿真与安全国家重点实验室,天津 300350)
1 研究背景
渗流导致的土体内部泥沙颗粒运动是坝体、河堤失稳破坏的重要原因[1-2]。根据泥沙运动形式的不同,渗流输沙分为管涌、流土、接触流土、接触冲刷等多种形式。据统计,世界上约有50%的坝体破坏是由于渗流所致的泥沙流失引起的[3-4]。因此研究渗流作用下的泥沙运动规律具有重要的实际意义。
管涌是渗流输沙的一种常见机制,常发生于洪水期的河堤及土石坝内部[5]。由于其严重的破坏作用,研究者们针对其内在机制和发展过程开展了大量的研究[6-7]。本文所研究的渗流输沙特指管涌现象。由于泥沙运动的过程是一个复杂的水土相互耦合作用的过程[8],从而很难用数学语言对其进行描述[9]。因此,在以往的研究中主要通过室内试验或是现场测试进行研究,并且利用试验结果建立经验模型,用来表达输沙率与各种参数之间的关系[7]。例如,Howard和McLane[10]基于土体受力平衡的理论,认为渗流的输沙量是由斜坡坡角与临界坡角的相对关系决定的。以此为基础,Fox等[11]提出了渗流剪应力的计算方法,并且利用试验数据提出渗流输沙量和渗流剪应力的经验关系。Chu-Agor等[12]提出了垂直河岸的渗流输沙模型,认为输沙量是和渗流流量相关的函数。梁越等[9]在其流固耦合模型中假设了输沙量与渗流流速之间的关系。另外,水力梯度是渗流中的一个重要参数,渗流输沙的起动条件也常用水力梯度描述[13-14]。比如Cividini等[15]通过抽水井周围渗流场中的泥沙输运试验,建立了土体细颗粒的密度随水力梯度的变化关系。再如Sterpi[16]利用取自意大利米兰的黏土进行研究,得到了不同渗流梯度情况下泥沙可动颗粒的流失规律。Fox等[17]利用室内的水平渗流试验结果,得出了渗流输沙量与水力梯度以及临界水力梯度的关系。总结已有的经验模型发现,渗流输沙率常被描述为以下关系
q=Kx(X-Xcr)a
(1)
式中,q为输沙率;Kx和a为与土体相关的参数;X为土体的渗流场参数,根据上文,X可表示渗流切应力、渗流流量、渗流梯度、渗流速度等;Xcr为发生泥沙运动时X的临界值。
近年来,随着研究手段的发展和研究思想的创新,新的研究方法也被利用来研究渗流输沙问题[9,18-19],但是多数的数学模型依然通过经验方法计算输沙量[12,16]。该类数学模型能够较完整的模拟出渗流输沙过程以及土体结构响应规律[9,20]。但是,由于输沙过程仍是由经验公式计算而来,缺少对颗粒运动机制和运动状态的定量描述。因此,其研究成果的普适性还存在问题[21],经验公式中的参数确定还存在诸多困难。此外,研究者也试图采用颗粒流方法模拟渗流输沙过程[22-23],模拟过程中能较好的捕捉泥沙颗粒运动轨迹和运动速度[24]。但是该类方法计算效率不高[25],所采用的土体条件和水力条件过于理想化,模型的验证以及对实际管涌现象的模拟还存在缺陷[21]。在这样的背景下,亟需一种渗流输沙的理论计算模型来弥补管涌模拟模型的不足。根据河流动力学的基本理论,土颗粒运动状态是精准把握输沙率的重要指标参数[26]。而渗流作用下土体内部颗粒的运动状态是极为复杂的,而且存在很大的随机性[27]。随着管涌的不断发展,颗粒运动的数量和强度均会发生明显变化[28]。因此,如何精准描述土颗粒的运动状态成为渗流输沙研究中重要的科学问题之一。
本文从泥沙颗粒的受力状态出发,推导泥沙颗粒在渗流场中运动的控制方程。通过分析渗流流速的概率分布模式,将单颗粒泥沙运动规律扩展到整个渗流场,并由此计算得到泥沙运动概率和输沙规律。通过和试验结果的对比,表明该模型具有合理性,可以对一维渗流作用下的泥沙运动规律进行描述。
2 材料和方法
2.1 动力学方程
如图1所示,渗流场中单颗粒受力包括渗流力和水下重力[13]。其中渗流力包括2部分,即由于压力差引起的渗流梯度力以及由于流动引起的水流拖曳力[29-30]。
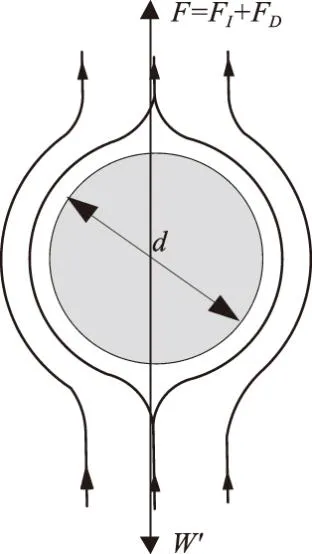
图1 土体内部可动颗粒的受力分析
颗粒所受渗流力F和水下重力W′表达式为
F=FI+FD
(2)
(3)
式中,FD为水流拖曳力;FI为渗流梯度力;D为颗粒直径;ρ′为颗粒的水下密度。
FD[26]和FI[31]的表达式分别为
(4)
(5)
式中,α为颗粒形状修正系数,对于球形取1,对于泥沙颗粒取1.7;CD为拖曳力系数;ρw为水的密度;ui为颗粒运动速度;ubi为孔隙内水流速度;I为水力梯度。
根据牛顿第二定律
(6)
将式(2)~式(5)带入式(6)可得
(7)
式中拖曳力系数与雷诺数有关,渗流作用下的颗粒雷诺数Re的计算公式为
(8)
式中,v为水的动力粘滞系数;u为流速,考虑到颗粒运动,u应是水流与颗粒的相对速度,即u=ubi-ui。由于渗流流速较小,一般小于10-3m/s,颗粒大小一般为毫米级,数量级也为10-3m。因此,渗流雷诺数一般小于1。此时拖曳力系数与雷诺数的关系由斯托克斯定律确定[26],即
(9)
将式(8)、式(9)带入式(7)可得
(10)
式(10)即为一维渗流作用下泥沙颗粒运动的控制方程。
2.2 临界起动流速
渗流梯度和渗流流速的关系服从达西定律
ud=KI
(11)
式中,K为渗透系数;ud为渗流流速。
引入平均孔隙流速,渗流流速与平均孔隙流速的关系为
(12)
式中,n为土体孔隙率。
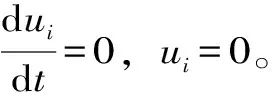
(13)
式(13)为颗粒运动的临界孔隙流速,其与临界水力梯度的关系为
(14)
可由式(13)和式(14)计算不同粒径的临界水力梯度。根据刘杰的研究成果[32],管涌是部分颗粒的运动,选取d5作为特征粒径进行临界水力梯度的计算是比较合理的。因此式(13)中,D=d5,d5为小于该粒径的土颗粒质量占总质量的5%。
2.3 颗粒运动状态分析
对于式(10),左右两边对t积分,并考虑到t=0时,ui=0,可得
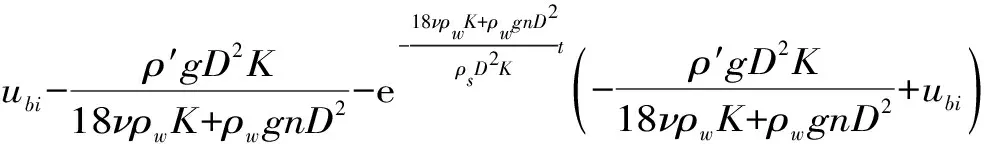
(15)
式(15)即为孔隙内单个土颗粒的运动速度表达式。
2.4 输沙率的确定
根据泥沙推移质运动理论,垂直渗流作用下,单位面积单位时间内的输沙率可由下式计算:
(16)
式中,q为单位时间单位面积的渗流断面上的输沙率;N为单位体积内可动颗粒的个数;V为可动颗粒的体积;P为可动颗粒运动概率。
N和V的表达式为
(17)
(18)
式中,PV为可动颗粒的体积比。
2.4.1P的确定方法
因为土体孔隙有大有小,孔隙内流速也呈大小不一的分布规律。只有孔隙内的流速大于土颗粒的临界起动流速,土颗粒才会被水流带走。但是如果颗粒运动轨迹中的下游孔隙小于颗粒直径时,土颗粒依然不能被水流带走。因此颗粒运动还应该满足一个条件,本文称为颗粒的输移条件,即颗粒输移必须满足下游孔隙大于可动颗粒的直径。所以这里的P包括两部分P1和P2,且P满足
P=P1P2
(19)
式中,P1为土颗粒的起动概率;P2为土颗粒的输移概率。假设土体内水流流动符合管流泊肃叶理论,管流速度和圆管半径的关系为[13]
(20)
这里假定公式(20)中的R服从均匀分布(0,2R),R为平均圆管半径,则可根据式(20)求得孔隙内流速ubi的概率分布为
(21)
因此,P1的计算公式为
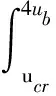
(22)
根据Hazen的研究[33],土体孔隙直径和颗粒级配有关:
D0=Bd10
(23)
式中,D0为孔隙直径;B为参数,取值为0.21~0.25;d10为土体特征粒径,表示小于该粒径的土颗粒质量占总质量的10%。由此可得P2的计算方法为
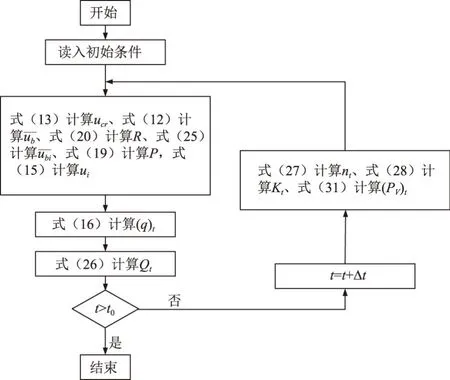
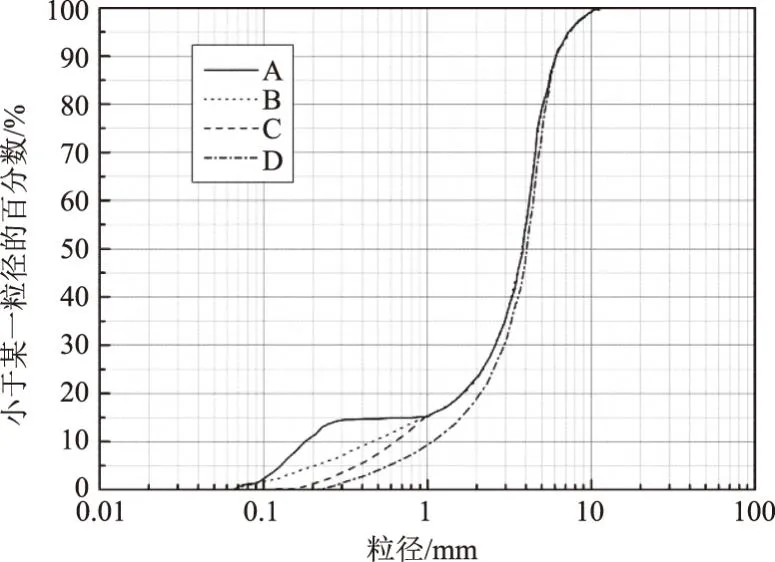
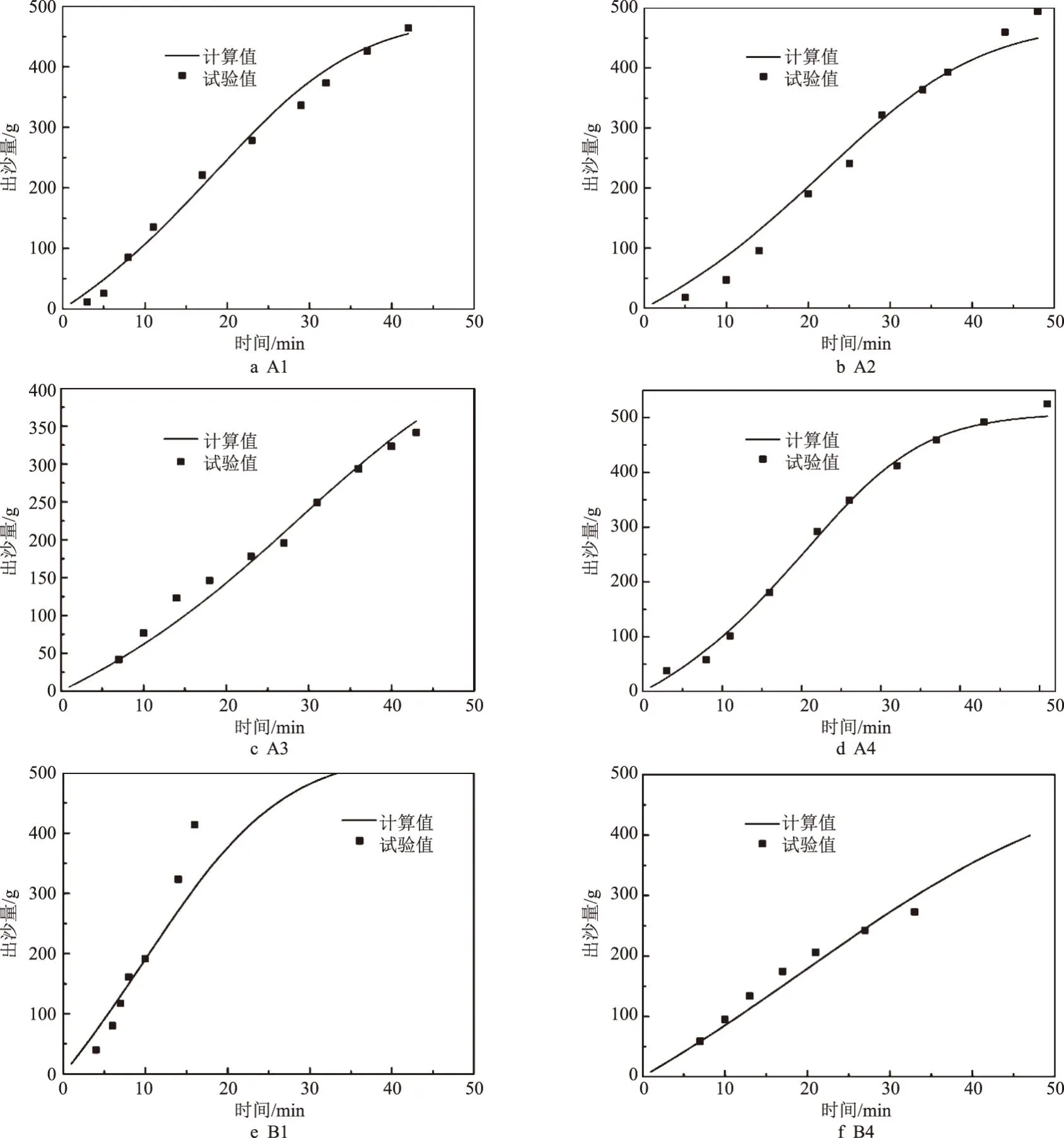
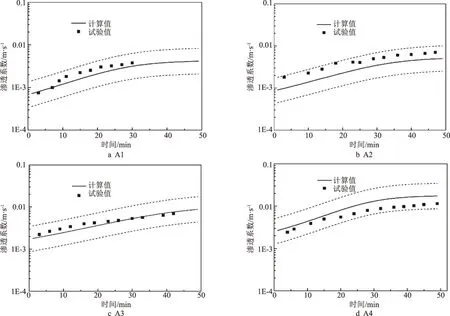
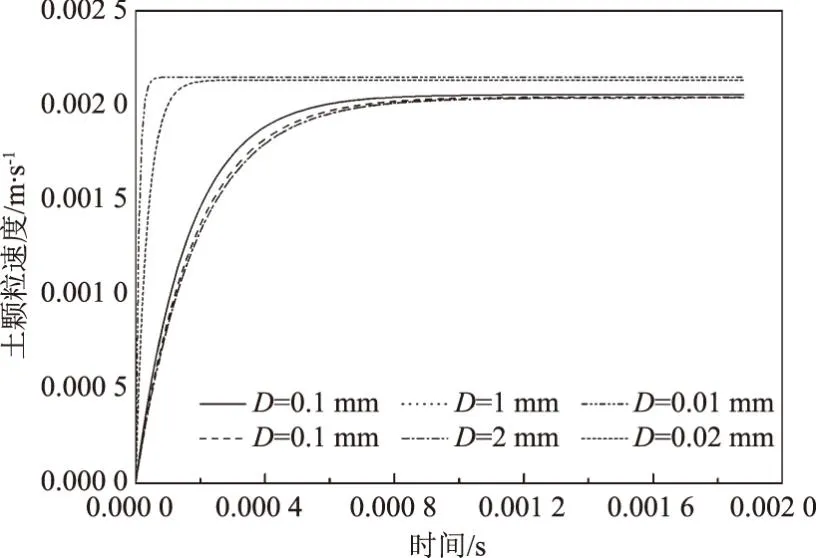
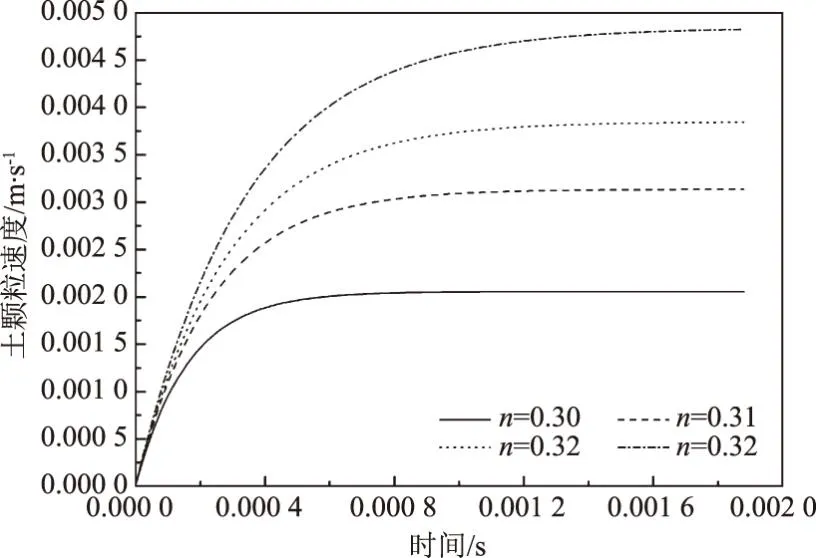
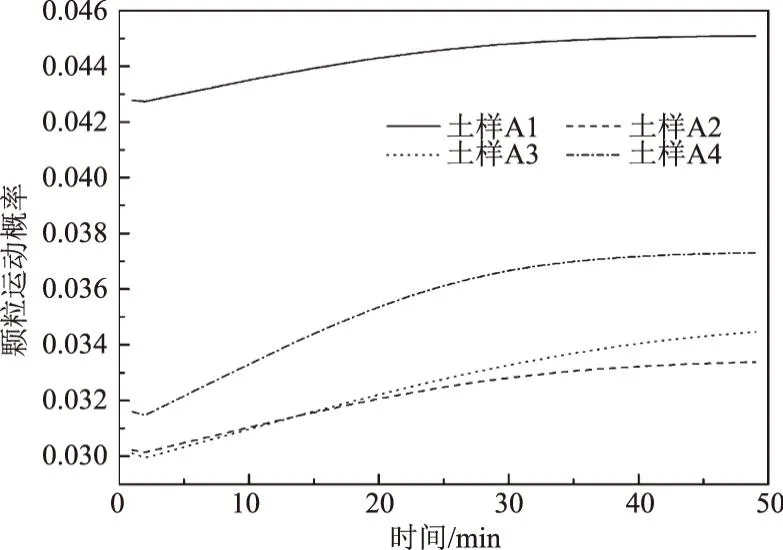
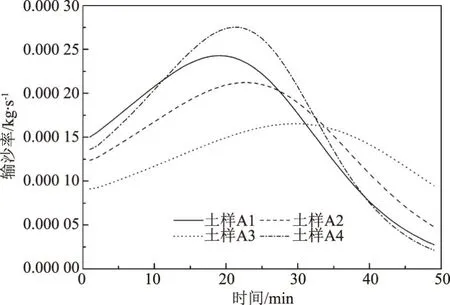
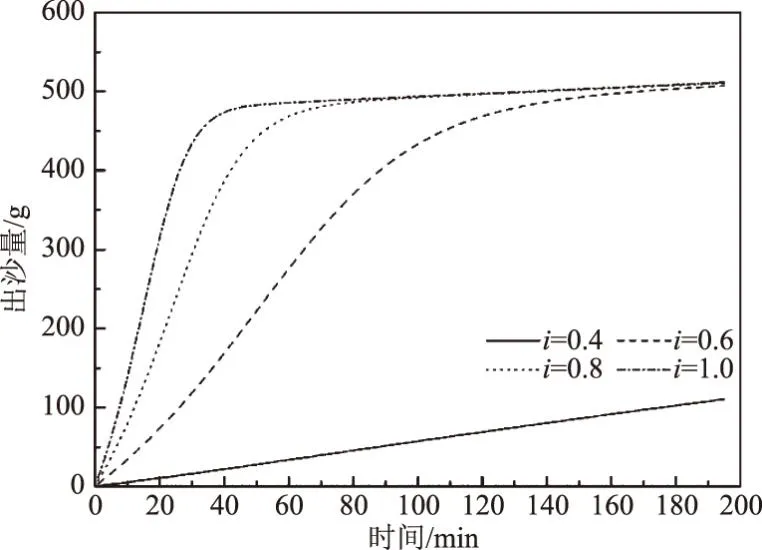
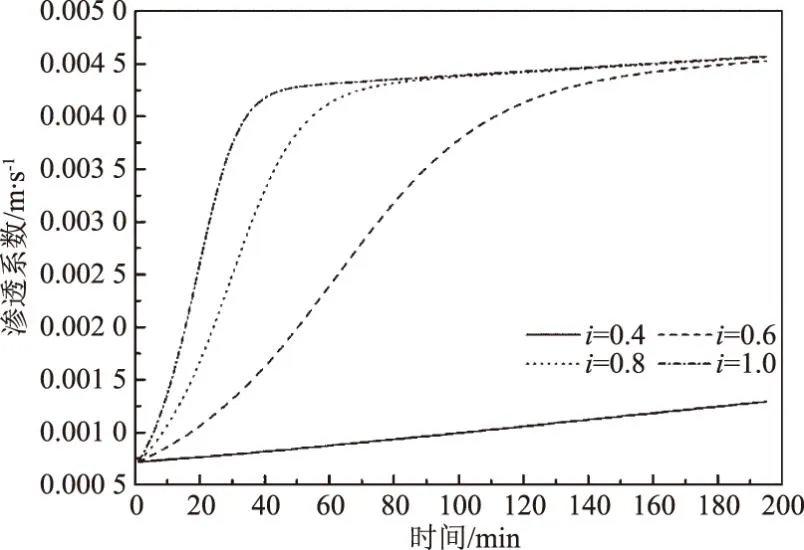
P2=P(D (24) 式中可根据土体级配的分布特征确定可动颗粒D0的大小,然后根据颗粒的质量比计算D小于D0的概率。 (25) 将式(15)、式(17)、式(18)、式(19)、式(25)带入式(16)可求得单位时间单位面积的输沙率。 前文已有论述,由于渗流输沙的过程伴随着渗流场的变化,因此对于输沙率的计算需要耦合渗流场的变化。t时刻相对于t-1时刻,土体的孔隙率n、渗透系数K、可动颗粒的体积分数Pv会发生变化。而其他变量,比如临界流速ucr、孔隙流速ub、起动概率P、孔隙半径R都可以由以上几个变量求解得到。因此,在已知t-1时刻各参数的值的情况下,只需确定t时刻n、K和PV的计算方法,就可实现时间上的迭代计算,进而实现渗流-泥沙场的耦合计算。 由输沙率q的定义可得在t时刻,总输沙量Qt的计算公式为 (26) 假设在输沙过程中,没有土体的变形,即输沙的体积即为土体中孔隙增加的体积。则 (27) 根据刘杰的研究[32],渗透系数的比值与孔隙率和d20有关。 (28) 假设水流带走的土颗粒均小于(d20)0,而且在渗流输沙的过程中,小于d20的颗粒粒径是均匀的,此时可以计算输沙Qt之后的(d20)t为 (29) 式中,(dx)0为可动颗粒的最大粒径;(Pm)t为粒径小于最大可动颗粒的土体所占的质量分数,其与输沙量Qt有关,即 (30) 式中,m0为初始时刻的可动颗粒的质量,将式(29)、式(30)带入式(28)可求得t时刻的渗透系数。 (PV)t为可动颗粒的体积占总颗粒体积的比值,其与输沙量的关系为 (31) 根据以上论述可通过式(27)、式(28)和式(31)实现渗流-泥沙场耦合计算,耦合计算流程如图2所示。 图2 耦合计算流程 许多研究人员对于渗流的临界水力梯度进行了试验研究,目前已发表的有4个经典的试验结果[14,28,34-35],这些试验都以无黏性土为研究对象,符合本文计算方法的前提条件。Skempton试验研究了4种级配土体的临界水力梯度,4组土体的级配如图3所示。图3中可以看出土样A和土样B级配较差,土体内部不稳,属于管涌型土,而土样C和土样D属于内部稳定性土体[36]。Ahlinhan试验中测定了5种土体在不同孔隙比情况下的临界水力梯度,其土体级配如图4所示,可以看出5组土样中,A1和A2土样级配较好,属于流土型土;E2和E3土样级配较差,属于管涌型土,而E1属于过渡性土[36]。Fleshman试验测定了天然沙的临界水力梯度,其土体级配如图5所示,其土样均为稳定性土体。陈亮试验测定了3种级配土体分别在4种孔隙率条件下的临界水力梯度,其土体级配如图6所示,可以发现土样A和土样B为管涌型土,土样C为过渡性土。4组试验结果与计算值的对比,如图7所示。本文计算方法与太沙基公式[37]的对比如图8所示。 图3 土样级配曲线(Skempton试验) 图4 土样级配曲线(Ahlinhan试验) 图5 土样级配曲线(Fleshman试验) 图6 土样级配曲线(陈亮试验) 图7 临界水力梯度的验证 图8 本文公式与太沙基方法的对比 根据图7,总体看临界水力梯度本文计算值与试验值接近(R2=0.79)。由图7可知,只有极个别的数据点在置信区间为95%的曲线外(图7中虚线),误差较大的数据点来自陈亮试验,其试验中测定的土样C在较小的孔隙率条件下临界水力梯度达到2.4~2.6,这在其他试验或文献中还未见到,一般当水力梯度如此大的情况下,任何粒径的土颗粒的重量都小于水力梯度力[23]。因此本文推测陈亮试验中,对应的这两组试验结果有测量误差。其他试验中,Skempton试验结果略微大于计算值,而Fleshman的试验正好相反,Ahlinhan的试验对应数据点分布在直线y=x两侧,与计算值较为接近。而从图8可以看出,本文的计算值要优于太沙基方法(R2=0.19),太沙基的计算结果对于不同土体差别不大,在其公式中仅包含土体密度和孔隙率的参数,而不同的土颗粒,其密度和孔隙率均相差不大,其公式对于不同级配土体的考虑并没有涉及。综上,本文的计算公式适用性更强。 陈亮在试验中测定了渗流出沙和出沙后的渗透系数[28],此外还列出了对于土样A在4种不同孔隙率条件下的出沙量和渗透系数的变化以及土样B在2种不同孔隙条件下的出沙量(土样C的临界水力梯度的试验存疑,此处并没验证),本文计算值与渗流输沙量的对比结果如图9所示。 图9 累积出沙量的验证 由图9可以看出,本文的计算值与试验值非常接近。出沙量随时间逐渐增多,且呈现出两个拐点。单位时间的出沙量,即输沙率是随着时间先增大,然后逐渐减小,最后基本为0。 在土颗粒不断流失的过程中,土体的孔隙率会逐渐变大,土颗粒也会逐渐变粗。该过程也会导致渗透系数的变化。在陈亮的试验中,同样测定了不同时刻的土体渗透系数,在文献[28]中,仅列出了土样A在4组不同孔隙率条件下的渗透系数的变化过程(如图10所示)。图10中实线为本文的计算值,上下2条虚线为2倍的计算值和1/2计算值。 图10 渗透系数的验证 由图10可知,土体的渗透系数随着时间是不断增大的,这是土体孔隙率变大而且土体的颗粒也变粗的结果[38]。本文的计算结果大致与试验值是一致的,试验测量的渗透系数值在1/2~2倍的计算值范围内,其中土样A1和土样A3与试验结果验证较好。事实上,渗透系数受多种因素的影响,目前的计算方法使得渗透系数在1/3~3倍的真实值范围内就已经非常困难[38-39]。另外,试验中精准测量土体的渗透系数也是非常困难的[40],因此本文得出的渗透系数的计算值与试验值吻合度较好。 式(15)列出了土体颗粒的运动状态方程,根据方程可知当渗流力大于重力时土颗粒做加速运动,土颗粒的运动速度是关于时间的函数,且与土体的颗粒大小有关。以文献[28]中的土体A1为例,计算不同粒径的颗粒由静起动的运动状态,如图11所示。由图11可知,土颗粒由静起动时的加速运动过程,其加速度是逐渐减小,直至减小为0。而不同粒径的颗粒的运动状态有所区别。当土颗粒粒径小于0.1 mm时,土颗粒的加速运动进程明显加快,颗粒运动达到平衡状态的时间较短,且达到平衡状态时的末速度稍大,这是由于小颗粒较为容易被水流带走而运动。当土颗粒粒径大于0.1 mm时,土颗粒的运动状态随粒径的变化区别不大,粒径从0.1 mm变化到2 mm的过程中颗粒的加速过程以及加速后的平衡状态差别不大。 图11 不同土颗粒的运动状态 对于同种土体,当土体孔隙率不同时,也可导致同粒径的颗粒运动状态不同,对于土体A1~A4,其差别在孔隙率和渗透系数的不同,这样对于同样的颗粒大小d10,不同土体中的运动状态如图12所示。由图12可知,在孔隙性增大的情况下,土颗粒的运动速度也会增大。这主要是因为孔隙性增大后导致渗透系数增大,在水力梯度不变的情况下,渗流流速会增大,这就导致土颗粒的所受渗流力增大,因此可见随着孔隙率的增加,几条曲线的斜率也在增加,土颗粒加速度增大。而土颗粒加速运动后的平衡速度也是随着孔隙率的增加而增大,这也是孔隙内水流流速较大造成的。 图12 不同孔隙性的土体颗粒的运动状态 2.4.1节中给出了土颗粒运动概率的计算方法,根据该方法可知在渗流输沙的过程中土颗粒的运动概率也是不断变化的。图13为土样A1~A4在渗流出沙的过程中,土颗粒运动概率的变化特征。由图13可知,出土颗粒的运动概率随着输沙过程是逐渐增大的。随着土体细颗粒的不断流失,土体的孔隙率和渗透性逐渐变大。根据式(22)所示,孔隙流速将有更大的概率大于临界流速,这时导致剩余土颗粒较为容易的发生起动,即P1将会增大。另外,由于细颗粒的不断流失,土体逐渐粗化,这时根据式(23)和式(24)土体的平均孔隙直径将会逐渐变大,土颗粒的输移概率P2也会增大。 图13 土颗粒运动概率 此外,通过与图9的对比分析可以发现,土颗粒的运动概率与细颗粒的累积流失量具有时间上的相关性。在颗粒流失的前20 min内,土颗粒运动概率增长速度很快,同时颗粒的流失速率也不断增强。在20 min之后,土颗粒流失曲线出现拐点,颗粒的流失量逐渐减缓,主要是因为土颗粒运动概率的增速减缓。通过输沙率(单位时间内的输沙量,如图14所示)的变化规律也能够看出颗粒运动概率与输沙过程的相关关系。渗流输沙率呈现出先增大后减小的趋势,这与梁越的理论模型的计算结果是一致的[9]。在输沙进行20 min内,输沙率逐渐增大,而在30 min后,除A3土体外,其余土样的颗粒运动概率几乎停滞增长,输沙率也开始大幅减小而出现了“拖长尾”的现象。根据式(16)中输沙率的计算方法,此时虽然颗粒运动速度和概率都较大,但是可动颗粒逐步流失,可动颗粒的数量成为制约渗流输沙强度的主要因素。 图14 不同土体的输沙率 本文以陈亮试验中的土样为例讨论孔隙率对出沙量的影响,在陈亮的试验中,孔隙比的大小在0.43~0.5之间,对应的孔隙率在0.3~0.33之间,孔隙率相差并不大,因此在其试验中,出沙量也是比较接近的。再者4种土样所受的水力梯度并不同,无法准确获得孔隙率这一单一要素对结果的影响。因此,本文以试验中的土样为例,假设土体的初始孔隙率分别为0.3、0.4和0.5,水力梯度都为0.6,计算不同孔隙率条件下的出沙量的值如图15所示。由图15可知,孔隙率越小,最终的出沙量越大;但是单位时间的出沙量(输沙率)即图中曲线的斜率,是随着孔隙率的减小而减小。这是因为,对于等体积的土体,孔隙率较大导致单位土体中的土颗粒的质量较小,可以被水流带走的细颗粒也较少,因此最终的出沙量是小于孔隙率较小的土体。而对于输沙率的变化规律则不同,由于土体孔隙率较大,细颗粒较为容易的从孔隙中流出,因此单位时间的出沙量就大于孔隙率较小的土体。另外,如前文所述,图15中曲线也可以看到有两个拐点。在水力梯度一定的情况下,影响出沙量的因素包括孔隙率和可动颗粒的数量。而在沙量逐渐流失的过程中,孔隙率不断增大,这能促进输沙;可动颗粒的数量逐渐减少,这能抑制输沙。图15中的输沙率先是增大然后减小,这说明在渗流输沙的初期孔隙率是影响输沙率的主要因素,而在输沙后期,可动颗粒的数量是输沙率变化的主要控制因素。 图15 初始孔隙率对出沙量的影响 以上3种孔隙率的土体,在0.6的水力梯度作用下,其渗透系数的变化如图16所示。图中可以看出,随着细颗粒的流失,土体的渗透系数是逐渐增大的。而随着孔隙率的增大,不同土体的渗透系数的增加幅度逐渐变大,即不同孔隙率土体渗透系数的差值随时间逐渐变大。这就是说,渗流输沙对孔隙率越大的土体的渗透性的影响也越大。另外,图16与图15表现出相同的规律,渗透系数随时间的变化也呈现出两个拐点,这也能证明孔隙率和可动颗粒的数量对输沙率的影响。 图16 初始孔隙率对渗透系数的影响 同样地,本文以陈亮试验中的土样为例讨论水力梯度的影响。假设土体孔隙率为0.3,而水力梯度分别为0.4、0.6、0.8和1.0,此时计算的出沙量和渗透系数变化分别如图17和图18所示。由图17、18可知,对于水力梯度0.4的土体,在200 min内,其出沙量要远远小于其他3个水力梯度,渗透系数的增长幅度也非常有限。这是由于0.4的水力梯度小于该土体的临界水力梯度,因此在较长时间内,渗流输沙量很少。其余3个水力梯度下,200 min内土体的最终输沙量都相等,差别在土体达到最大输沙量的时间上。当水力梯度较大,对渗流输沙的加速效应显著,输沙所需时间明显缩短。而且随着时间的推移,这种加速效应将逐渐增强。由图18可知,当水力梯度增加到1.0时,细颗粒将在30 min作用完全流失。在此过程中,较大水力梯度引起的输沙量增长迅速,最大能达到水力梯度为0.6情况下的3倍以上。同时伴随着土体渗透系数的快速增加。该过程也可通过本文的理论模型进行解释。当水力梯度较大,孔隙流速也更大,可动颗粒所受渗流力(如式(4)和式(5)所示)更大,从而导致土颗粒具有更大的运动速度和运动概率,渗流输沙的发展速度也将更快。 图17 水力梯度对出沙量的影响 图18 水力梯度对渗透系数的影响 本文针对渗流作用下泥沙输运过程,提出了泥沙颗粒运动的控制方程,并以此为基础建立理论模型,提出了渗流作用下输沙率的计算方法。利用试验数据验证了本理论模型的合理性。利用该模型对渗流作用下的泥沙运动状态和影响因素进行了分析,得出以下结论: (1)本文提出由土颗粒单颗粒受力规律出发,推导了土颗粒的运动方程,该方程可用来计算土体的临界水力梯度,通过与Terzaghi方法的对比,发现该计算方法可信度较高。 (2)土颗粒在由静起动的过程中做加速运动,加速历程很短,其运动特征与土颗粒粒径及孔隙率有关;渗流输沙过程中颗粒运动概率不断增加,主要是因为颗粒孔隙逐渐变大,可动颗粒受力增加,输运的几何容许度增加引起的。通过颗粒运动速度和运动概率可计算渗流输沙率,输沙过程与土颗粒运动概率具有很好的一致性。 (3)土体孔隙率和所处的水力梯度是影响渗流输沙率的重要因素。孔隙率较大,输沙率越大,总输沙量越小。水力梯度对输沙过程有明显的加速效应,且当水力梯度低于临界水力梯度时,土体颗粒流失明显变慢。 (4)通过对出沙量和渗透系数的变化规律的分析,得出在输沙的初始阶段,孔隙率是控制输沙率的主要因素,而在输沙后期,可动颗粒的数量是主要的限制因素。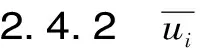
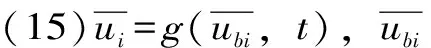
2.5 渗流-泥沙场的耦合计算

3 模型验证
3.1 临界水力梯度的验证

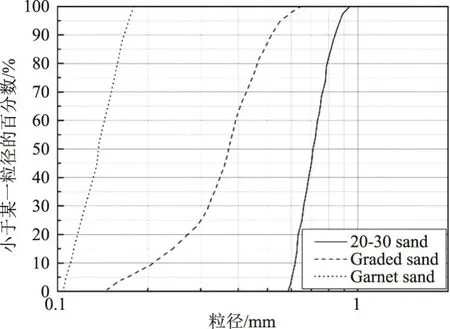
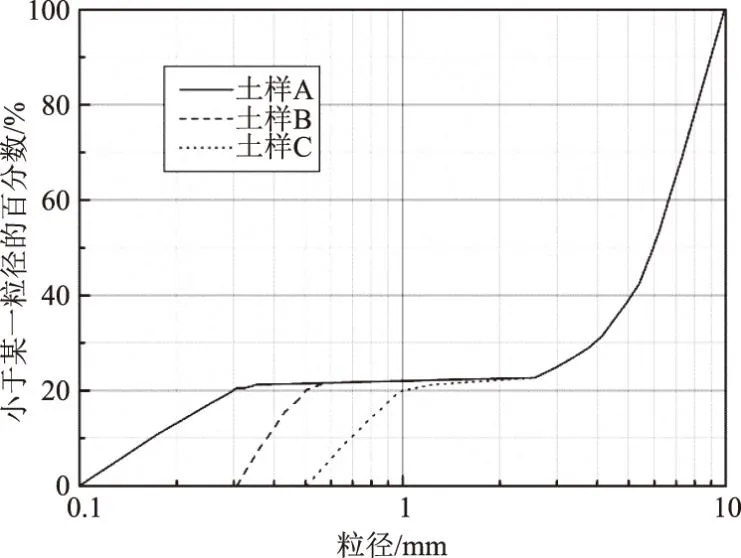
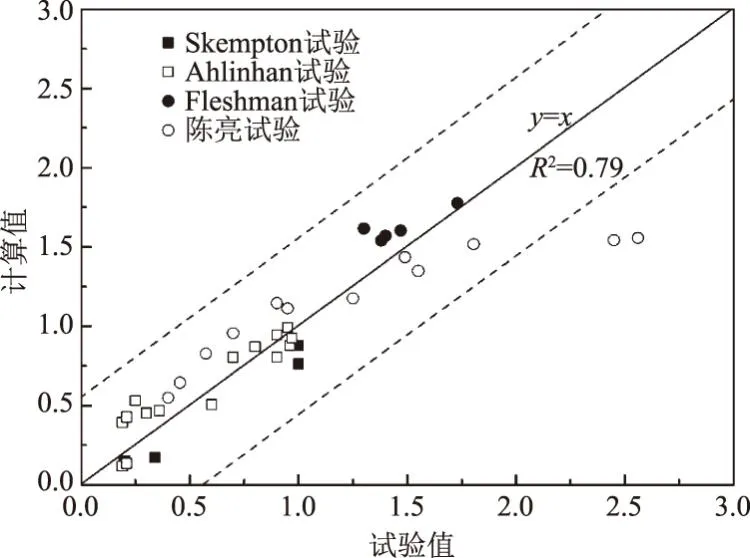
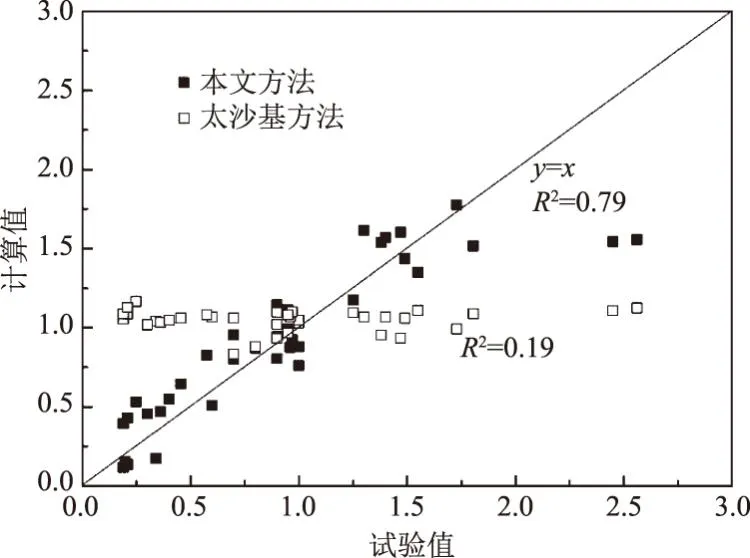
3.2 出沙量的验证
3.3 渗透系数的验证
4 结果分析
4.1 土颗粒的运动速度
4.2 土颗粒的运动概率和输沙率
4.3 初始孔隙率对输沙过程的影响
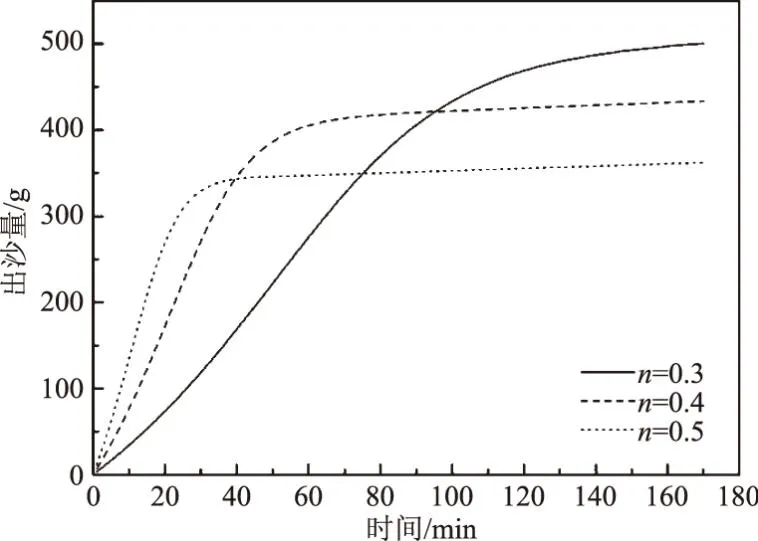
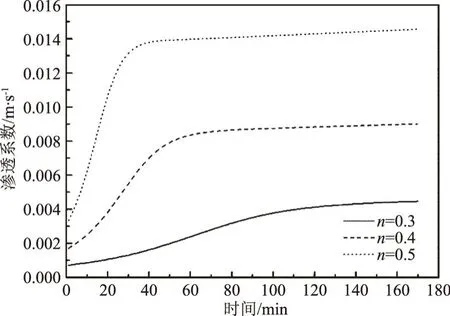
4.4 水力梯度对输沙过程的影响
5 结 论

