基于多机器学习的强夯有效加固深度预测对比研究
徐永兵,李家艳,关艳丽,唐木红,普新凯
(云南建投第一勘察设计有限公司,云南 昆明 650031)
0 引 言
随着一带一路、交通强国战略的部署和实施,大型基础设施建设(如高铁、码头、机场等)蓬勃发展。同时,坚守耕地红线,执行严格的耕地保护制度也使耕地与建筑用地供需矛盾日益突出。无论在我国西部山区还是东部沿海,随着可用土地数量的逐年减少,大规模的开山挖沟、填土造地已逐渐成为解决用地矛盾的有效对策[1]。对于云南省这样的西部山区,开山挖沟已是部分地州寻求发展的唯一选择。削山填谷这样的大型挖填工程不可避免存在十几米甚至上百米高的填筑体,填筑体失去了原有的结构性,较为松软,导致其承载力及密实程度很难满足于建筑的设计要求,在必须在建筑施工前采取一定的地基处理措施,使得其能达到一定的安全储备[2]。
地基强夯法是建筑工程中常用的技术,可有效改善地基的强度和稳定性,提高建筑物的安全性和可靠性。强夯法最开始由法国Menard公司在20世纪70年代提出[3],经过多年的发展与应用,我国现行的规范[4]将强夯法纳入地基处理的重要方法,成为造价省、工期短的地基处理方法。其有效加固深度是判别加固效果的重要依据,直接影响关系到强夯能级和施工工艺的选择[5]。影响强夯有效加固深度的因素众多,主要分为3类:①锤重、锤底面积、落距等设备因素;②夯点击数、夯击遍数、间歇时间等强夯设计参数;③土体粒径、饱和度、相对密度等岩土体因素[6-7]。整个强夯过程作用机理复杂,影响因素繁多。关于强夯有效加固深度的研究最早由L. Menard[3]提出,奠定了计算有效加固深度的系数修正公式和经验公式的基础。后续学者通过工程实践与室内外试验,总结了施工工艺、岩土体特性、强夯设计参数等因素的各类形式的经验公式。目前,我国现行的方法主要是规范查表法、系数修正法、经验公式法等,这些方法简单易用。但其精确度较低,在有些工程应用上误差较大,较难满足于当前强夯法安全、经济的市场需求。
近年来,随着计算机算法模型和计算机硬件性能的不断提升,使得以机器学习算法为代表的数据驱动模型已成为许多学科研究的常用方法。如今算法模型常用的有BP神经网络模型、支持向量机(SVM)模型[8]、随机森林(RF)模型[9]、多层感知器(MLP)[10]模型等。在各个学科中都出现了算法模型的身影,且都发挥了较好的应用效果,但至今确鲜有学者将机器学习应用于强夯有效加固深度研究。为此,本文尝试利用既有的工程实际资料,结合BP神经网络模型、SVM模型、RF模型、MLP模型、XGBoost模型以及朴素贝叶斯模型等6种机器学习算法模型,对强夯有效加固深度进行预测。为对比各模型的预测精度及可靠性,以云南某在建项目作为实例工程验证,旨在为预测强夯法有效加固深度提供一种经济有效的方法,同时促进机器学习模型在岩土工程学科中的应用。
1 数据与模型
鉴于岩土工程的介质材料自身的复杂性,在岩土设计和施工中往往都是依赖于经验判断的指导。强夯有效加固深度不仅受到岩土体的复杂性控制,也受到强夯设计参数等因素有影响。采用机器学习算法处理这种复杂且非线性程度很高的工程难题具有较强优势,这也是当前人工智能颇受青睐的重要原因之一。
1.1 数据预处理
1.1.1 数据可行性验证
机器学习算法实现的重要基础是算法训练,要求提供有特定的输入、输出数据形成训练集样本和输出集样本。参照张鑫等[11]研究基础,从我国地基处理工程现场及相关文献资料中选取648个强夯地基处理样本[12-13]。该样本集的输入数据有干密度、含水量、夯击能量、夯锤面积4项输入,输出数据为实测得到的强夯有效加固深度。模型原始数据集见表1。

表1 模型原始数据集
对于训练样本需要保证各因子之间的独立性,要进行相关性分析,剔除相关性较大的因子,规避因子间的相互干扰。将表1中的648个数据作为样本,计算因子之间的相关系数,并根据相关性计算结果绘制成因子相关性热力图,见图2。从图2可知,此样本数据最大Pearson相关值为0.65,反映出因子间不存在高度相关性[14],数据样本具有一定的代表性。

图1 样本因子相关性热力图

图2 不同模型夯实有效加固深度预测值与实测值对比
1.1.2 数据归一化处理
表1中样本数据具有不同的特征及量纲,且数据样本还具有较高离散性。为消除数据之间的量纲影响,增强数据之间的可比性,需要对样本数据进行归一化处理。将样本数据分别归一化至区间[-1,1]内,得到归一化处理后的数值Xout,公式为
(1)
式中,Kmax、Kmin分别表示归一化后数据的最大值与最小值,为1、-1;xi为第i个值;Xmax、Xmin分别为原始数据集每列数据的最大值、最小值组成的矩阵;E为单位矩阵。
归一化后的数据样本能最大化的消除奇异数据导致的不良影响,同时提高模型预测精度、加快模型的收敛性。模型归一化处理后数据集见表2。

表2 模型归一化处理后数据集
1.2 预测模型
本文采用当前应用较广且较为成熟的6种算法模型,即BP神经网络模型、SVM模型、RF模型、MLP模型、XGBoost模型以及朴素贝叶斯模型分别进行强夯有效深度训练及预测。
(1)BP神经网络模型是一种误差反向传播的多层前馈网络,是当前应用最为广泛的神经网络模型之一。其过程是不断迭代的信息正向传播与误差反向传播,各层的权值在迭代的过程中不断调整,直至收敛。
(2)SVM模型最早就是为了解决小样本、非线性等问题所提出的。其求解过程可以理解为是处理1个凸二次规划问题,从理论上可以得到全局的最优解,可以解决传统神经网络中不能避免的局部最优化问题。
(3)RF模型基于分类树算法,通过利用大量分类树的汇总从而提高预测精度,对于异常值和噪声具有很好的适应性,能较好处理大量的输入样本的非线性算法模型。
(4)MLP模型具有较高的容错性和鲁棒性,是够适用于各类连续变量与离散变量,其突出的非线性映射能力适用于结果各类复杂数据分类工作.
(5)XGBoost模型以CART算法为子模型,是通过Boosting实现多棵树的集成学习方法。由多个弱分类器集成而构建形成的强分类器,其在回归和分类上都有很好的表现,目前在股市、房价、生物医学等各个领域都能看到XGBoost模型的身影.
(6)朴素贝叶斯模型是当前应用最为广泛的分类算法之一,通过统计得到各种状态在不同特征下的先验概率和条件概率,再计算给定样本在各种状态下的后验概率,将最大后验概率对应的类别判定为样本所属的类别。保证朴素贝叶斯算法中数据间的相互独立性是核心要素,这也是朴素二字的含义所在,因此称为朴素贝叶斯算法。
2 模型训练与对比
2.1 模型训练
6种模型适用同样训练集样本与输出集样本,并将训练集样本与输出集样本分为训练样本与检验样本,两者比例设置为7∶3。模型训练好后将训练集样本输入模型进行强夯有效深度的预测,再将预测值与实测值进行对比。截取具有代表性的36个典型项目作为对照样本,6种模型夯实有效加固深度实测值与预测值对比见图2。
2.2 模型精度对比
为对比6种不同的机器学习模型的性能和效果,采用均方根误差σRMSE、平均绝对百分比误差σMAPE、决定系数R2以及平均绝对误差σMAE这4项指标对比各模型的预测准确率、误差、泛化能力等。均方根误差σRMSE反映了预测数据与真实数据之间偏离的程度,其值越小反映模型的预测精度越高;平均绝对百分比误差σMAPE的范围为[0,+∞),其值越近于0,表示模型越完美;决定系数R2≤1,其值越接近于1,表示模型的预测精度较为准确;平均绝对误差σMAE反映误差值的大小,其值越大反映模型的误差越高;评价指标的计算公式为
(2)
(3)
(4)
(5)
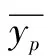
6种不同的机器学习模型预测精度对比见表3。从表3可知,RF模型σRMSE值最小,为0.137,表明预测性能比较优异;BP神经网络模型、SVM模型与MLP模型σMAPE值普遍偏大,表明其属于劣化模型;RF模型与XGBoost模型R2值较高,为0.905与0.861,表明预测精度相对较高;RF模型与XGBoost模型σMAE值在0.1左右,预测值的可靠性较高。通过对比6种模型,RF模型性能较为优异,其次为XGBoost模型与朴素贝叶斯模型,BP神经网络模型、SVM模型与MLP模型表现较差。
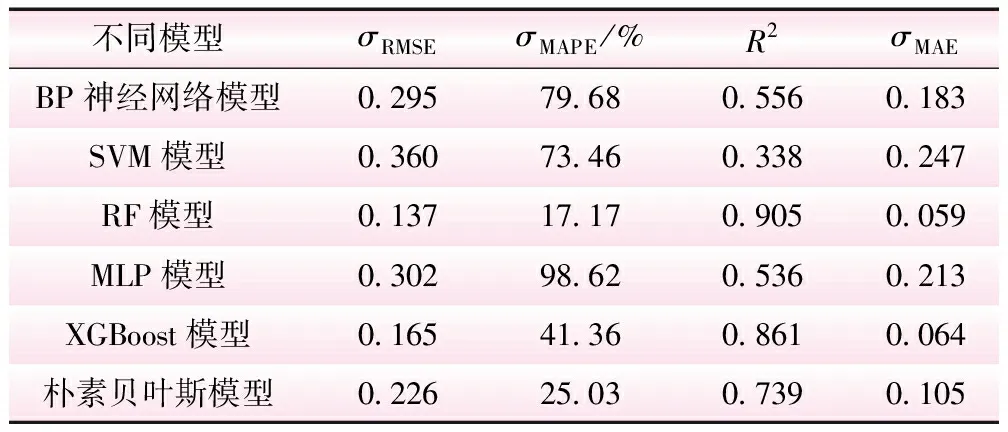
表3 模型精度对比
3 工程实例应用
3.1 工程概况
项目位于云南省泸西县城东北,白水塘水库西南,S203以东,泸弥高速以北。项目占地面积约为782.54 hm2,场平面积约550.6 hm2,为新建某产业园,场地整平、地基处理妥善是项目落地的根本保障。项目分为2个回填区,为红黏土强夯处理工程,红黏土为干密度为16.6 kN/m3,含水量为 15.7%。夯锤直径为2.52 m,面积为4.98 m2。2处区域分别采用5 000 kN·m和4 000 kN·m的夯击能量,经过现场实测数据,有效加固深度分别为5.35 m和4.21 m。为更好地对比模型的应用效果,测试数据引用文献[11]中的工程实例资料,具体工程实例数据样本集见表4所示。

表4 工程实例数据样本集
3.2 应用效果对比
为检验各模型的精度及适用性,以工程实例数据为检验样本集,采用6种模型预测强夯有效加固深度,并与实测结果进行对比,结果见图3。从图3可知,经过6种模型的预测结果和实测值进行比较发现,RF模型预测性能表现优秀,预测结果与实测值相当接近;其次为XGBoost模型与朴素贝叶斯模型也表现出不俗的预测性能。
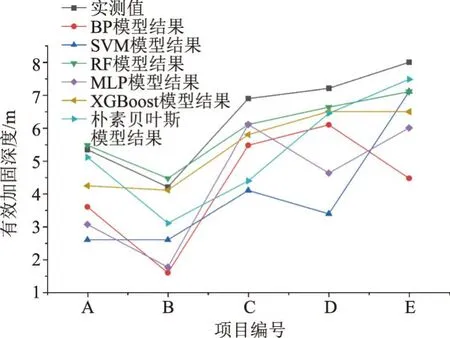
图3 各模型预测值与实测值对比
为进一步检验模型的预测精度,开展定量评价。同样采用均方根误差σRMSE、平均绝对百分比误差σMAPE、决定系数R2以及平均绝对误差σMAE这4项指标,计算得到各模型的精度检验值。6种模型实例应用精度对比见表5。从表5可知:

表5 各模型实例应用精度对比
(1)BP神经网络模型、SVM模型与MLP模型对应的R2小于0,说明这3种模型整体预测性能较差,模型的拟合效果差于平均预测误差,存在明显的欠拟合。其本质原因在于BP模型与MLP模型都是一种基于反向传播算法的前馈神经网络,受数据量不足、过拟合、局部最优等问题的影响。因此在小样本的数据情况下,预测效果较差;SVM模型在小样本情况下,会因对训练数据的过度拟合而失去泛化能力,需选择合适的核函数和正则化参数来处理非线性和噪声问题。
(2)XGBoost模型与朴素贝叶斯的预测性能也未达到理想效果。分析其原因在于XGBoost模型通过迭代构建多棵树拟合残差,并使用正则化项控制过拟合。然而,在小样本情况下,XGBoost模型难以找到合适的树结构和参数,导致欠拟合或过拟合。此外,XGBoost模型也需要调整多个超参数,如学习率、树深度、子采样比例等,这些超参数对结果影响较大,但在小样本情况下难以通过交叉验证或贝叶斯优化等方法进行有效地选择。同样,朴素贝叶斯模型通过计算先验概率和似然概率来得到后验概率,并进行分类或回归预测。然而,在小样本情况下,朴素贝叶斯模型可能遇到数据稀疏性问题,即某些特征值或类别在数据集中出现次数过少或为0,导致概率估计不准确或为0。
(3)RF模型的拟合程度最高。原因在于RF模型可以利用生成对抗网络进行样本扩充,从而增加数据的多样性和稳定性[15],使其能够有效地处理高维小样本数据的分类或回归问题。
(4)对比6种模型,在小样本的情况下,RF模型性能较为优异,其次为XGBoost模型与朴素贝叶斯模型,BP神经网络模型、MLP模型与SVM模型表现较差。因此,针对今后类似的工程项目且样本数据有限的情况下,建议优先选用RF模型。
4 结 语
针对于强夯有效加固深度研究远落后于实践的问题,本文提出采用机器学习的方式将部分强夯影响因素与强夯有效加固深度建立联系,通过机器学习对多数据的快速分析和处理,解决预测强夯有效加固深度这类复杂的非线性问题,结论如下:
(1)借助于智能化的机器学习模型,可通过少量且简单的强夯数据预测强夯有效的加固深度,为工程应用提供良好的参考建议。
(2)机器学习的训练精度取决于数据样本的数量与质量,本文所收集到的数据样本较少,在一定程度上限制了部分模型的预测精度。在小样本的情况下,RF模型性能较为优异,其次为XGBoost模型与朴素贝叶斯模型,BP神经网络模型、MLP模型与SVM模型表现较差,建议在样本数据有限的情况下,优先选用RF模型。
(3)影响强夯有效加固深度的因素众多,本文选用的训练样本仅涉及干密度、含水量、夯击能量、夯锤面积这4项因素,今后在实际工程应用中可再细化影响因素,补充训练样本,提升模型的实际适用性,进一步提高模型的预测性能。

