新型区域电力系统电源规划和时序生产模拟
蒋 攀,孙万光,张新宇,周立洋
(1.中水东北勘测设计研究有限责任公司,吉林 长春 130021;2.水利部寒区工程技术研究中心,吉林 长春 130061)
0 引 言
20世纪以来,全球能源结构加快调整,新能源技术水平和经济性大幅提升,风能和太阳能利用实现跃升发展,规模增长了数十倍。2022年我国发电装机25.67亿kW,其中风电、光伏发电装机占比达到29.5%[1]。《“十四五”现代能源体系规划》指出“推动构建新型电力系统,促进新能源占比逐渐提高,全面推进风电和太阳能发电大规模开发和高质量发展”。风电和光伏等新能源具有显著的时序波动特性[2],消纳问题突出,需要在发电侧与储能电源互补发电。抽水蓄能是当前技术最成熟、经济性最优、最具大规模开发条件的调节电源,与风电、太阳能发电、核电、火电等配合效果好。加快发展抽水蓄能,是构建以新能源为主体的新型电力系统的迫切要求,是保障电力系统安全稳定运行的重要支撑,是可再生能源大规模发展的重要保障。
以新能源为主体的新型区域电力系统中,电源主要包括风电、光伏、火电、水电、抽水蓄能等。规划水平年,在风电、光伏、水电装机容量确定的条件下,抽水蓄能规划需要解决的主要问题:①抽水蓄能最优配置容量是多少;②抽水蓄能电站的系统节煤量是多少。开展电力系统电源规划和生产模拟是解决上述问题的核心和关键。
生产模拟是电力系统规划与运行优化的基础,通过模拟电力系统运行过程,预测各机组的发电量、燃料消耗及排放量,为制定合理的电源规划方案或运行计划提供依据[3]。时序生产模拟分为2类[4]:①启发式时序生产模拟方法;②基于优化求解技术的时序生产模拟方法。启发式时序生产模拟方法将时序负荷曲线转化成持续负荷曲线,通过合理安排各类电源在持续负荷曲线上的位置和出力水平,模拟电力系统发电调度过程,进而计算系统总的生产成本。在新型电力系统下,该方法的缺点比较明显:难以准确地反应负荷和新能源出力特性变化对系统运行的技术经济指标的影响;随着电源结构日趋复杂,不同类型电源机组间协调平衡策略设计难度加大。基于优化求解技术的时序生产模拟方法的核心是以系统运行成本最小为目标的机组组合模型,即满足系统运行约束和机组运行约束,通过优化进行技术决策各类电源所有机组启停状态和出力大小。机组组合问题是一个包含整数变量和连续变量的非线性规划问题,基于混合整数规划(Mixed integer programming,MIP)的机组组合模型获得了广泛应用。
受限于现有的数学方法和技术能力,基于MIP的机组组合模型仍然难以直接应用于区域电力系统中长期时序生产模拟,通常采用短周期(24或168个时段)滚动求解技术顺序求解,但该方法无法处理机组检修等跨周、跨月问题。邵成成等[5]提出了含大规模清洁电力系统的多时间尺度生产模拟方法,中长期模拟考虑清洁能源季节分布,制定常规机组检修计划,短期模拟以检修计划为边界,对机组组合问题进行精细模拟。对于区域电力系统,各类常规电源机组数量逾百台,即使采用短周期滚动进行技术求解,求解规模仍然较大,而机组集群技术可降低求解规模、加快求解速度,并且具备较高精度。机组集群是将大规模机组组合的二进制变量转化为单个整数变量,进而降低求解规模,在电力系统长期运行管理和电源发展规划等方面取得广泛应用[6-7]。但相关研究表明,机组集群技术关注集群整体出力水平,而忽略了出力在机组间的分配,当电力系统灵活性不足时,在机组启停阶段,机组集群模型的解是次优解甚至是不可行解[8]。
在区域电力系统电源规划和时序生产模拟中,需同时考虑机组检修及机组组合问题,计算时段总长为1 a。机组组合问题计算时段步长为1 h,年计算时段总数为8 760。由于区域电力系统电源组成复杂、机组数量庞大,即使采用机组集群技术,同时求解机组检修及机组组合问题仍然十分困难。因此,本文采用机组检修与机组组合耦合求解框架[5],提出一种中等规模机组集群方法,衔接机组检修与机组组合优化,降低优化求解规模的同时保证单元机组检修的连续性,可较准确计算火电机组煤耗。
1 新型区域电力系统生产模拟框架
1.1 框架
新型区域电力系统生产模拟由机组检修优化模型和机组组合优化模型构成。机组检修优化模型的主要功能是根据新能源出力年内分布及负荷特性确定机组检修计划,促进新能源消纳,并保证系统空闲容量年内均匀分配,当规划水平年确定新能源、水电装机规模后,给定抽水蓄能装机容量方案,确定系统对火电最小需求容量。机组组合优化模型的主要功能是根据检修计划确定的边界条件,开展逐小时(全年8 760 h)生产模拟,计算系统全年运行指标。由此可见,二者为单向、松散耦合模式。
机组检修优化模型计算时段为周,计算得出年内逐日机组检修状态。机组组合优化模型计算周期为1 d,计算时段为1 h,以逐日机组检修计划为边界,根据检修计划确定开机容量,以系统煤耗最低为目标,计算系统总煤耗,开展机组组合优化计算;以前一日末尾时刻机组状态作为当日开始时刻机组初始状态,进行逐日顺序、滚动模拟。
1.2 中等规模机组集群方法
在机组组合优化中,一般将特性相同或相近的机组组成一个集群机组,可提高计算效率,但在与机组检修优化耦合时存在较大困难。检修优化计算时,若以单个机组为计算单元,计算量大,求解困难,并且与机组组合优化中的集群机组无法直接耦合。若以机组组合中的大规模集群机组为计算单元:①采用二进制整数变量表示检修状态,集群机组规模大,同时检修不合理;②采用整数变量表示检修状态,无法准确描述集群机组中的检修分配,不能满足单个机组检修连续性约束。
本文提出中等规模机组集群方法,为避免集群机组规模过大,将大规模集群机组拆分成若干中等规模集群机组,机组检修优化模型和机组组合优化模型中采用相同的集群机组。检修优化模型中,采用二进制整数变量表示检修状态,集群规模应满足检修场地约束。机组组合优化模型中,采用整数变量表示开机状态,中等规模机组集群示意见图1。
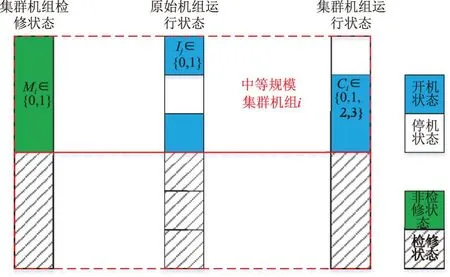
图1 中等规模机组集群示意
中等规模机组集群方法可使机组检修与机组组合优化直接耦合,保证单个机组检修的连续性,降低求解规模,提高求解速度,并具有较高的精度。
以火电为例,机组集群规模的确定方法如下
(1)
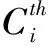
2 新型区域电力系统机组检修优化模型
在以新能源为主体的新型区域电力系统中,机组检修优化模型一方面考虑清洁能源的年内分布问题,另一方面考虑系统空闲容量年内分配问题。在电源规划中,当新能源及水电装机容量确定后,通常采用多方案比选确定抽水蓄能最优配置容量,即假定若干抽水蓄能容量方案,各方案通过增减火电容量来满足系统负荷需求,要求各组合方案系统煤耗最小且空闲容量最少。为了减小求解规模,机组检修优化通常采用分块负荷曲线(Load block curve,LBC)[5],但该方法无法考虑负荷的时序波动性[9],无法充分考虑抽水蓄能机组的检修安排。
从宏观角度上看,在新能源发电量大的时段尽量安排火电机组检修,有利于新能源消纳;在系统残余负荷(系统负荷减去新能源出力)峰谷差较小时段尽量安排水电和抽水蓄能机组检修,促进新能消纳的同时满足系统对调峰容量的需求。该策略最终目的是降低系统运行煤耗。本文提出新型区域电力系统机组检修优化模型,以系统空闲容量(火电、水电、抽水蓄能)最小为目标函数,以系统电力平衡、调峰容量平衡为约束条件,同时考虑机组检修连续性约束、检修场地约束、检修时段约束等约束条件。
2.1 目标函数
采用系统空闲容量最小为目标函数,表达式为
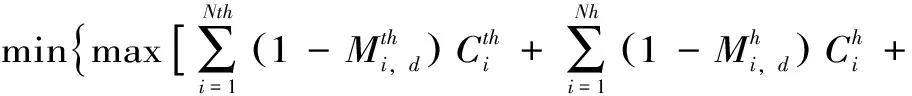
(2)
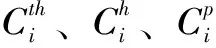
选用该目标函数的主要目的:在给定系统负荷、风电和光伏出力上限条件下,根据给定的抽水蓄能容量,确定系统所需的火电最小容量,以此来分析抽水蓄能可替代火电容量,当火电容量小于系统所需最小容量时,各电源的检修计划无论如何优化都不能满足系统运行要求。
2.2 约束条件
(1)系统电力平衡约束
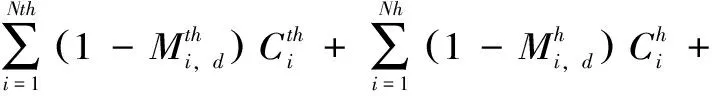
(3)
(2)系统调峰容量平衡约束。大规模新能源并网后,系统残余负荷的峰谷差进一步加大,检修安排若不合理,则会导致大量新能源弃电,且系统煤耗增加。通过调峰容量平衡约束,可避系统残余负荷峰谷差较大时段安排水电和抽水蓄能机组检修,有效提高新能源消纳,表达式为
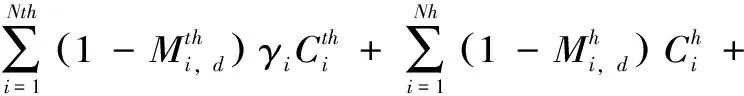
(4)
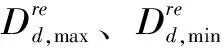
(3)其他约束。机组检修状态为0、1整数约束,0代表非检修状态,1代表检修状态。检修连续性约束,各机组检修期间连续停机。检修场地约束,主要控制同一时段检修机组台数。检修时段约束,主要控制水电机组汛期不检修,供热机组冬季供暖期间不检修。
3 新型区域电力系统机组组合优化模型
3.1 目标函数
该模型以总成本最小为目标函数,总成本包括系统的火电发电成本和弃风、弃光、弃水经济损失之和,即
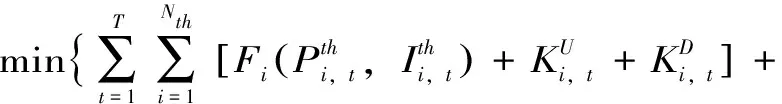
(5)
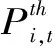
3.2 约束条件
约束条件主要包括:负荷平衡约束、机组出力上下限约束、储能约束、水电站电量约束、备用容量约束等。对于区域电力系统电源规划时序生产模拟,火电机组的爬坡能力约束不是主要约束条件,本文不考虑此约束条件。
(1)负荷平衡约束。电力系统各电源时段出力之和等于系统时段负荷,表达式为
(6)
式中,Ii,t为机组i在时段t的启停状态;Pi,t为机组i在时段t的有功出力。
(2)机组出力上下限约束。适用于风电、光伏、火电、水电、抽水蓄能等电源。对于风电和光伏出力,上限为相应风、光条件下的机组最大出力,下限为0;对于水电,上限为预想出力,下限为最小技术出力;对于抽水蓄能,上限为装机容量,下限为0;对于火电,上限为装机容量,下限为最小技术出力,表达式为
Ii,tPi,min≤Pi,t≤Ii,tPi,max
(7)
式中,i=1,2,…,N;t=1,2,…,T。
(3)储能约束。储能约束条件表达式为
(8)
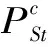
(4)水电站电量约束。考虑不同水文年平均出力确定的电量约束,表达式为
(9)

(5)备用容量约束。旋转备用加负荷备用的备用率取8%,由火电、水电、抽水蓄能共同承担;冷态备用的备用率取5%,全部由火电机组承担,表达式为
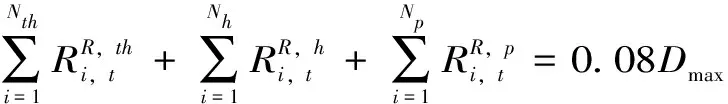
(10)
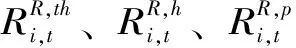
3.3 机组集群
中等规模机组集群方法对水电、抽水蓄能电站模拟精度较高,与单台机组的机组组合模拟差别不大。但对火电而言,中等规模机组集群方法在机组集群运行煤耗、启停机煤耗等方面与单台机组组合模型差别较大。为了准确计算系统运行煤耗,对中等规模火电机组集群进一步采用机组集群求解方法[6,10-13]。
(1)集群机组组合状态。集群火电机组i由Ji台相近机组组成,开机容量在相邻时段间变化的约束表达式为
(11)
机组状态变量约束条件为
0≤Ii(t),Ui(t),Di(t)≤Ji
(12)
(2)集群机组出力约束。集群火电机组i在时段t的输出功率Pi(t)满足约束
(13)
式中,αi(t)为集群火电机组i的最小技术出力率,由单机最小技术出力率加权平均获得。
(3)最小启停机约束。火电机组并网后,必须保证一定的运行时间才可以停机,机组停机后也必须保证一定的停机时间才可以并网发电,集群机组最小启停机约束表达式为
(14)
(15)
式中,MUTi、MDTi为最小启动和停机时间。
(16)
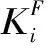
集群机组i的启动成本和停机成本函数为
(17)
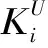
4 算例分析
4.1 区域电力系统概况
某区域电力系统规划水平年(2035年)最高负荷29 100 MW,用电量1 600亿kW·h,最大外送容量为30 000 MW,年送电量为1 800亿kW·h。该区域电力系统电源组成包括风电、光伏、火电、水电、抽水蓄能等。规划水平年风电装机容量60 000 MW,光伏装机容量31 500 MW,水电装机容量2 330 MW。经系统电源优化配置,确定抽水蓄能装机容量为19 500 MW(包括已建、在建抽水蓄能2 400 MW,新增17 100 MW)。新能源占系统规划电源装机的比例为59.4%,比重较高,抽水蓄能电站对电力系统内新能源的消纳将起到非常重要的作用。规划水平年,本网负荷及外送年电量为3 400亿kW·h,各月电量见图2。风电年装机利用小时数2 300 h,光伏年装机利用小时数1 600 h,规划水平年新能源(风电+光伏)逐月发电量见图3。
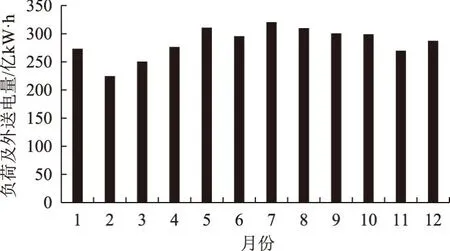
图2 逐月负荷及外送电量
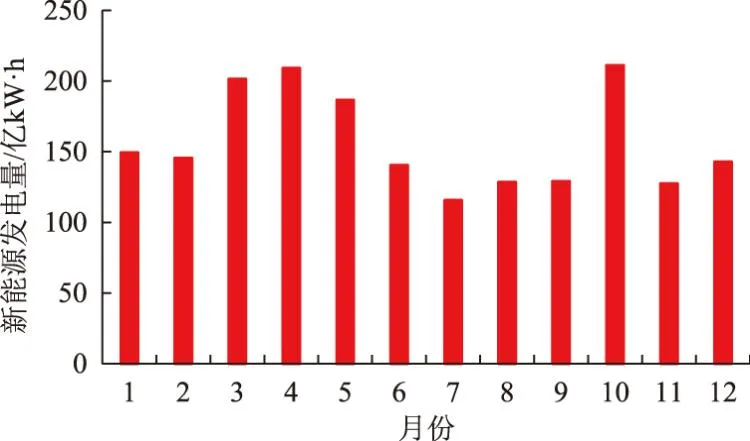
图3 逐月新能源发电量
从图2、3可见,负荷及外送电量7月份为年内最大值,2月份为年内最小值;而新能源发电量10月份为年内最大值,7月份为年内最小值。由此可见,新能源发电量年内分布与系统所需电量间匹配性较差。
4.2 检修优化模型计算结果分析
经检修优化模型计算,规划水平年系统火电容量为40 900 MW时,满足电力平衡约束和调峰容量平衡约束,且系统空闲容量最小。根据各电源装机容量及计算条件限制,火电划分为20个集群机组,水电划分为9个集群机组,抽水蓄能划分为15个集群机组。火电检修时长为45 d,水电及抽水蓄能机组检修时长均为30 d,考虑热电机组供暖期不检修、水电机组汛期不检修,同时保证机组检修的连续性,得出各类电源集群机组检修计划,结果见图4。
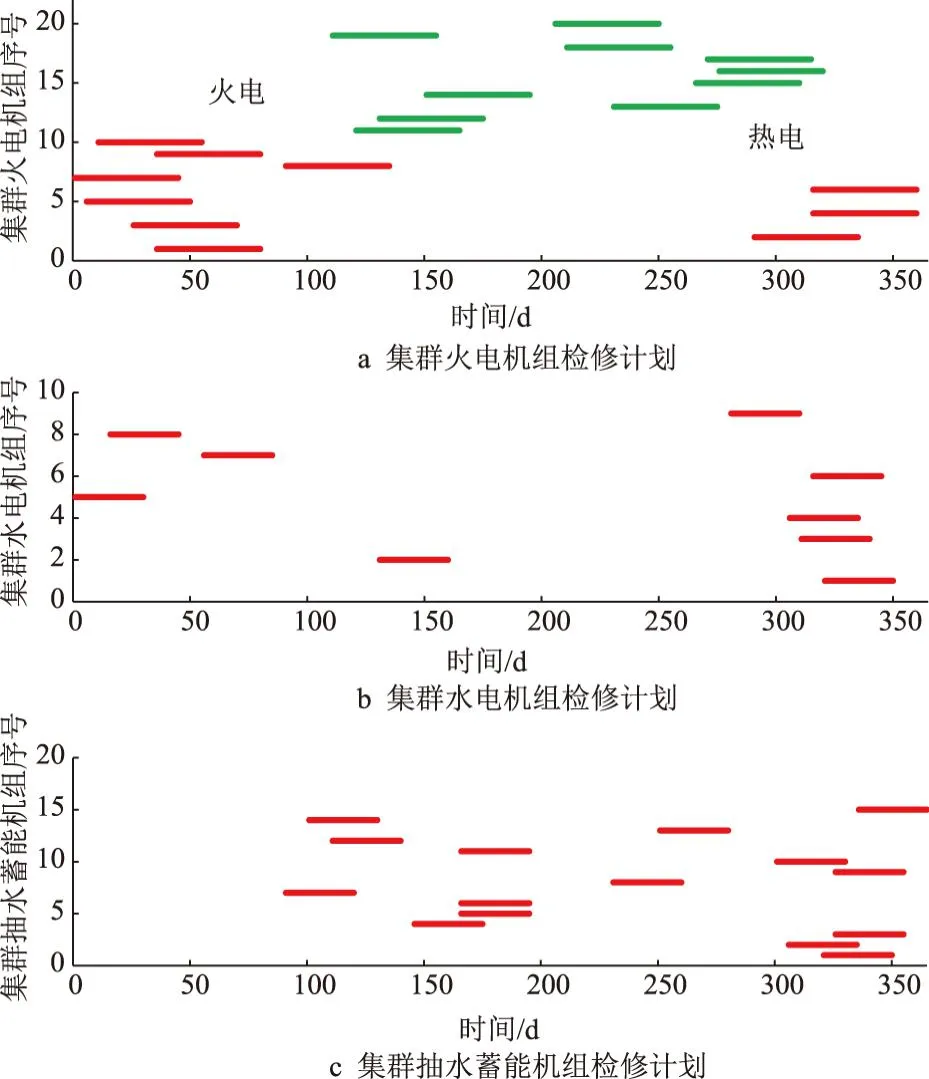
图4 各类电源机组检修计划示意
从图4可见,受供热机组供暖期不检修约束,供热机组主要集中在夏秋季检修,非供热机组主要集中在供热期检修;2月为全年负荷最低时段,3月~5月以及10月份新能源发电量较大,火电机组安排检修容量较大,有利于新能源消纳。新能源发电量较大月份,抽水蓄能机组安排检修容量较小,主要用于调节新能源出力,提高新能源消纳程度。
机组检修优化模型确定的各类电源检修计划安排,充分考虑了负荷及新能源发电量的年内分布特性,利用年内低负荷时段和新能源发电量大的月份集中检修火电机组,新能源发电量较大月份尽量少安排抽水蓄能机组检修,促进新能源消纳,同时留有尽可能多的抽水蓄能容量用于系统的调峰和填谷,降低系统整体运行成本。
4.3 机组组合优化模型计算结果分析
以检修优化模型计算结果为边界条件,对规划水平年8 760 h机组组合优化问题进行求解,并与启发式时序生产模拟方法计算结果进行对比,结果见表1。
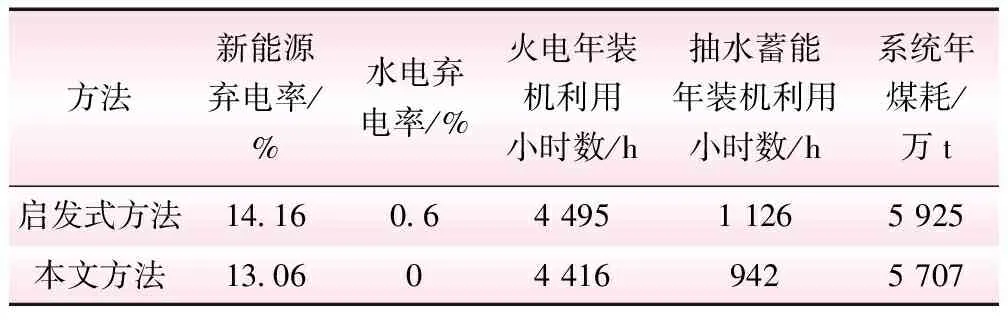
表1 模拟结果对比
从表1可见,新能源弃电率方面,启发式方法新能源弃电率为14.16%,本文方法新能源弃电率为13.06%,多吸纳新能源电源电量21亿kW·h;水电弃电率方面,启发式方法为0.6%,本文方法为0,减少水电弃电量0.22亿kW·h;火电年装机利用小时数方面,启发式方法为4 495 h,本文方法为4 416 h,较启发式方法减少79 h;抽水蓄能年装机利用小时数方面,启发式方法为1 126 h,本文方法为942 h,较启发式方法减少184 h;系统年煤耗方面,启发式方法为5 925万t,本文方法为5 707万t,较启发式方法减少218万t,节能效益十分显著。
与启发式方法相比,本文方法从机组检修安排上就充分考虑了新能源发电量的年内分布以及系统负荷特性,有效促进了新能源消纳;采用中等规模机组集群方法,保证单元机组检修的连续性;采用机组组合优化求解方法,并对中等规模火电机组集群进一步采用机组集群求解方法,较准确的计算系统运行煤耗以及启停煤耗,对各类电源间出力协调平衡进行全局寻优。
选取夏季(7月)、冬季(12月)典型月份,绘制设计水平年各类电源逐小时出力过程如图5所示。
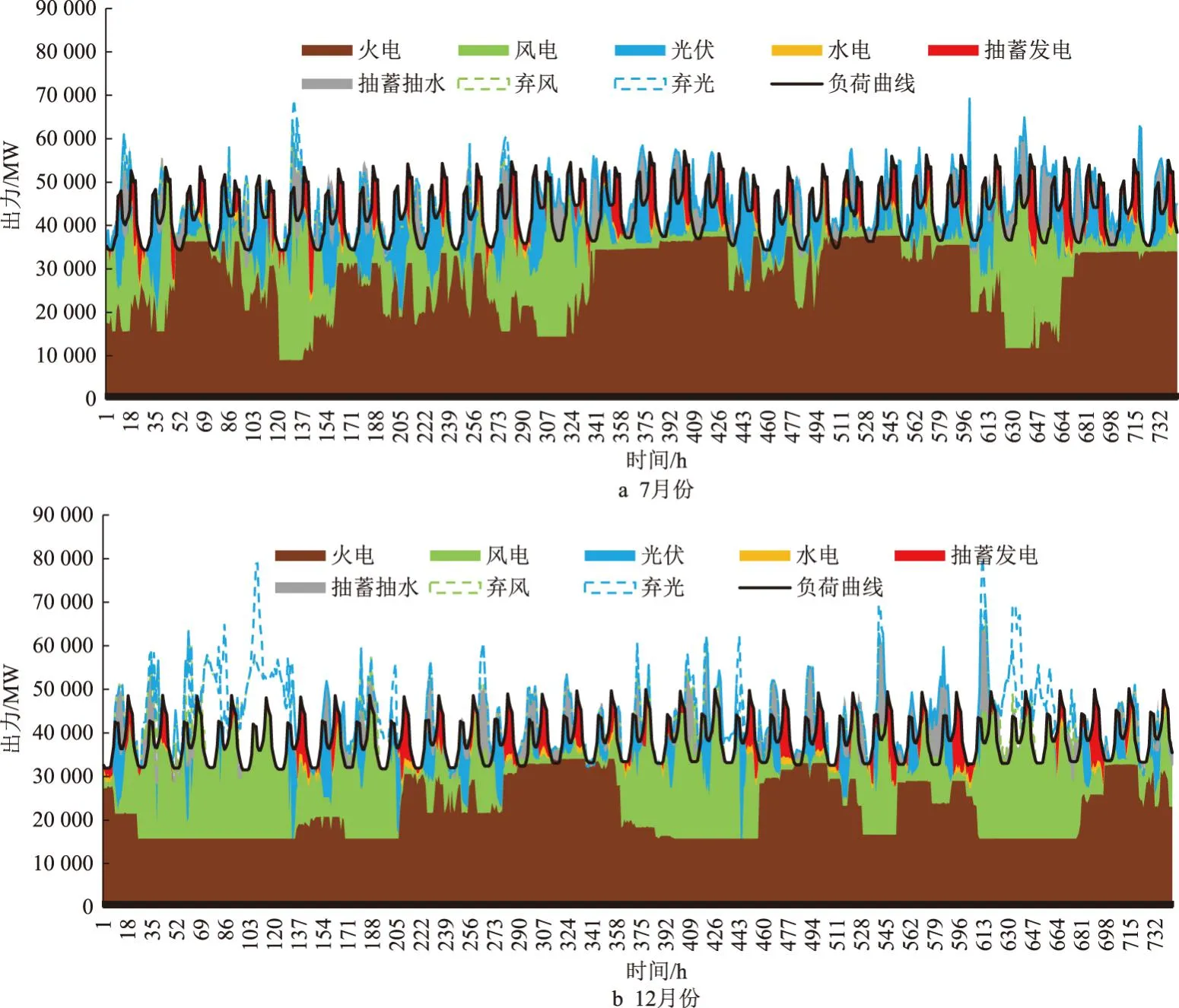
图5 设计水平年(2035年)夏、冬季典型月份各类电源出力过程
5 结 语
(1)本文设计了区域电力系统机组检修计划与机组组合的双层耦合框架,提出了中等规模机组集群方法,可使机组检修与机组组合优化直接耦合,保证单台机组检修的连续性,降低求解规模,提高求解速度。
(2)提出了新型区域电力系统检修优化模型,以系统空闲容量最小为目标函数,考虑系统电力平衡约束、调峰容量约束,以及检修连续性约束、检修场地约束和检修时段约束等约束条件。在其他电源容量确定的条件下,可计算出火电必需容量;各类电源机组检修安排充分考虑新能源发电量年内分布及系统负荷特性,促进新能源消纳。
(3)在机组组合优化模型中,以系统运行成本最小为目标函数,并考虑弃风、弃光、弃水成本,对中等规模火电机组集群进一步采用机组集群求解方法,较准确计算火电运行及机组启停煤耗。在区域电力系统时序生产模拟中,本文方法计算结果明显优于启发式方法,可对各类电源间出力协调平衡进行全局寻优。

