基于响应面法的水下不分散混凝土性能影响因素研究
曾 涛,窦立刚,刘利民,邓 超,卫学典
(长江三峡技术经济发展有限公司,湖北 宜昌 443133)
混凝土水下浇筑时受到水流的冲洗作用,会造成浆骨分离,影响施工质量[1]。而水下不分散混凝土技术的出现使得混凝土拌合物在水中能够抵御水流的冲洗作用,其技术的关键是添加一种水溶性高分子化合物外加剂——絮凝剂[2-3],也称作抗分散剂。混凝土抗分散剂价格较其他外加剂要高3~4倍,使用抗分散剂后1 m3混凝土的成本大概增加300元左右[4]。但相较于围堰法、垂直导管法等传统水下浇筑混凝土的施工方法[5-6],水下不分散混凝土不仅能简化水下施工工艺,还能缩短施工周期,降低水位涨跌对施工进度的影响,总体经济效益反而有所提升。
现阶段水下不分散混凝土的配合比设计方法主要是基于经验判别和室内试验。通常的程序包括配合比计算、性能试验、结果评估、配合比优化调整、反复循环这一系列操作,直到混凝土各项性能达到预期,由此带来试验周期长、效率低、资源消耗多等问题。响应面法相较于试验法,虽然计算过程相对复杂,但一方面能减少试验次数,另一方面能够建立各因素对水下混凝土性能的影响和因素间相互作用的数学模型,供后期性能预测,节约成本[7-8]。
絮凝剂掺量、减水剂掺量和水泥用量是影响水下不分散混凝土性能的关键因素。本文通过析因设计原理设计了絮凝剂掺量2.0%、2.5%、3.0%,减水剂掺量1.5%、2.0%、2.5%,单位体积水泥用量450、500、550 kg三变量三水平混凝土配合比试验,探究了上述因素对水下不分散混凝土抗分散性能、工作性能、力学性能的影响。基于响应面法建立参数水平与混凝土性能的回归模型,分析得出最优掺量,对水下不分散混凝土配合比设计提出优化建议。
1 原材料及试验方法
1.1 原材料性能
水泥采用某厂家供应的42.5级普通硅酸盐水泥,水泥物理性能及化学组成检测结果见表1。减水剂采用上述厂家生产的PCA-I(标准型)高性能减水剂,外加剂性能与匀质性检测结果见表2;引气剂采用该厂家供应的GYQ型引气剂。试验用粗骨料为5~20 mm级配的玄武岩人工碎石,细骨料为玄武岩人工砂。

表1 水泥物理性能检测结果

表2 减水剂物理性能与匀质性检测结果
絮凝剂采用某厂家供应的SBT®-NDA水下不分散混凝土抗分散剂,外加剂性能与匀质性检测结果见表3,符合相关标准要求[9]。

表3 掺絮凝剂物理性能与匀质性检测结果
1.2 试验方法
依据DL/T 5117—2021《水下不分散混凝土试验规程》[10]开展试验,本研究测试新拌混凝土拌和物的坍落度来评价水下不分散混凝土拌合物的工作性能,测试悬浮物含量来评价水下不分散混凝土的抗分散性能。水下成型均采用150 mm×150 mm×150 mm的标准立方体试模,标准养护至28 d龄期后开展抗压强度试验。
2 试验设计与试验结果
2.1 技术要求
水下不分散混凝土设计强度等级为C30,坍落度为230±20 mm。
2.2 配合比设计与试验结果
响应面法(Response surface methodology,RSM)是一种综合性试验设计和数学建模优化的方法,通过对具有代表性的局部各点进行试验,建立拟合全局范围内各因素与结果间的函数关系,可取得各因素最优水平值,并能够研究多种因素间交互作用对目标响应值的影响[11]。试验基准配合比如表4所示。

表4 C30水下不分散混凝土推荐配合比
选取普通硅酸盐水泥掺量、絮凝剂掺量和高性能减水剂掺量为关键因素,坍落度、悬浮物含量、28 d龄期抗压强度为目标优化值,设计三因素三水平试验,利用Design Expert(Version∶13.0.1.0)软件对试验结果进行响应面分析。各因素水平原材料掺量如表5所示。试验结果如表6所示。表中前12组为析因试验组,后5组为中心掺量重复试验组。
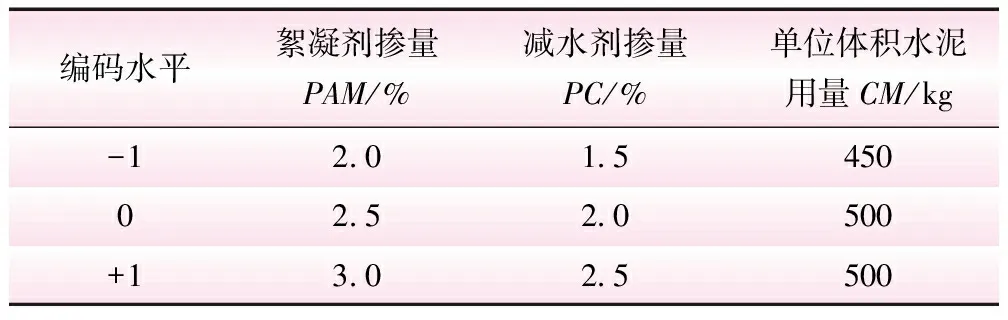
表5 试验因素及编码水平
对试验结果采用二次曲线(quadratic)进行拟合,建立回归模型
(1)
式中,X为自变量影响因素;Y为响应预测值;β0为常数项;βi、βii、βij分别为一次、二次、交互回归系数;n为因素数量;i、j表示n个因素中的第i个和第j个。
采用方差分析对拟合得到的二次回归模型的方差和回归系数进行显著性检验,各目标值模型的相关系数、F值(整体回归方程显著性检验)和P值(单个变量系数的显著性检验)如表7所示,以各实测值和预测值为横纵坐标绘制散点图,得到各响应面模型预测值与实际值的对比如图1所示。其中坍落度、悬浮物含量和抗压强度回归模型的相关系数分别为0.891 5、0.939 0和0.887 0,各回归模型的散点均匀分布在y=x直线及直线两侧位置,说明模型拟合效果良好,可靠性较强,可根据该回归模型进行多因素相关性分析。
显著性检验中,F值和P值反映了二次模型方程中每个回归系数的重要性。对于每个回归系数来说,F值越大、P值越小说明该回归系数越重要,当P值小于0.05时视为该参数对目标值的影响显著性高,反之该参数显著性较低[12]。
3 试验结果与分析
3.1 工作性能
通过拟合建立的水下不分散混凝土工作性能预测模型为
Y1=-10.62PAM+16.25PC+21.88CM-2.5PAM×
PC-8.75PAM×CM+10PC×CM-7.88PAM2-
1.63PC2-5.37CM2+202
(2)
式中,Y1为坍落度;PAM、PC和CM分别为絮凝剂、减水剂和水泥掺量。
各关键因素对水下不分散混凝土坍落度的影响规律如图2所示。为使变化规律明显展示,分别截取自各个变量固定某一水平时,另外两个变量的相互作用的响应曲面及对应的等高线图,后文同。
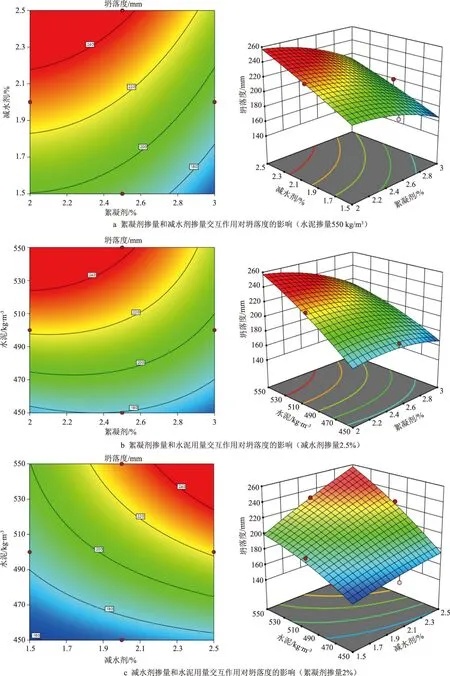
图2 三因素交互作用对混凝土坍落度的影响
通过对等线图和响应面曲面图各个因素进行分析,可判断各单因素对混凝土坍落度的影响规律及显著性程度[13]。
从图2a可知,当絮凝剂掺量固定某一水平时,随减水剂掺量的增加,混凝土坍落度逐步增加,当减水剂固定某一水平时,随絮凝剂掺量的增加,混凝土坍落度逐步降低;减水剂轴上的等高线密度大于絮凝剂,即减水剂对坍落度影响的显著性要大于絮凝剂,絮凝剂掺量固定2.0%时,减水剂掺量由1.5%上升至2.5%造成坍落度由200 mm增加至240 mm,减水剂掺量固定1.5%,絮凝剂掺量由2.0%上升至3.0%造成坍落度从200 mm降低至180 mm。
从图2b可知,随着水泥掺量的上升坍落度增加,絮凝剂掺量为2.0%时,水泥掺量从450 kg/m3增加至550 kg/m3造成坍落度从180 mm增加到240 mm,而当水泥掺量处于低水平时,絮凝剂掺量对坍落度影响很小。
从图2c可知,随着二者掺量增加,坍落度增加,水泥掺量影响的显著性大于减水剂。
综合分析以上信息可知,3个关键因素对混凝土坍落度影响显著性的大小依次为水泥、减水剂、絮凝剂,与方差分析的结果吻合。
响应曲面可以直观地描述因素间的交互作用对响应值的影响规律,响应面扭曲程度越大,等高线曲率越大,各因素间的交互作用影响越显著,对比图2a、图2b、图2c可知,图2b的扭曲程度稍大于图2c,图2a最小,即各组合影响显著性大小顺序为水泥和减水剂、絮凝剂和水泥、絮凝剂和减水剂。此外,随着减水剂和水泥掺量的增加,混凝土坍落度增加,说明二者的相互作用对混凝土坍落度有显著正面影响,其余因素组合相互作用对坍落度均有负面影响,但并不显著。结果均符合方差分析结果。
3.2 抗分散性能
通过拟合建立的水下不分散混凝土抗分散性能预测模型为
Y2=-17.25PAM+6PC+14.75CM-0.75PAM×PC-
5.75PAM×CM+1.75PC×CM-2.13PAM2-
2.63PC2-4.12CM2+118
(3)
式中,Y2为悬浮物含量;PAM、PC、CM含义同前。
各关键因素对水下不分散混凝土抗分散性的影响规律如图3所示。
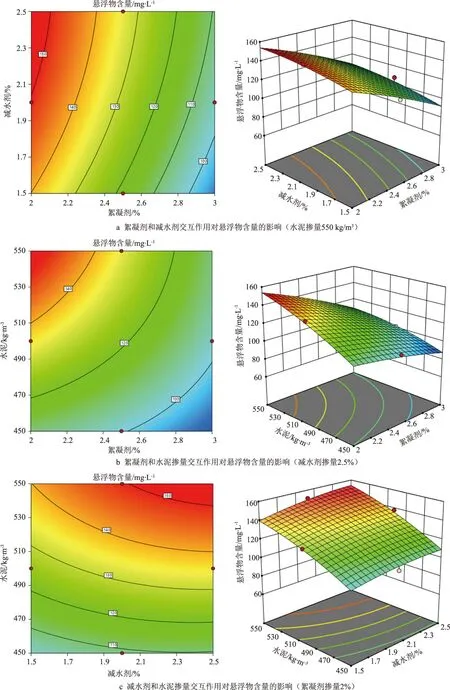
图3 三因素交互作用对混凝土悬浮物含量的影响
从图3可知,随着絮凝剂掺量的增加,悬浮物含量降低,拌合物抗分散性增强,随着减水剂掺量的增加,悬浮物含量上升,混凝土抗分散降低;絮凝剂轴上等高线的密度远高于减水剂,说明絮凝剂对抗分散性的影响远高于减水剂,当减水剂掺量为1.5%时,絮凝剂掺量从2.0%增加到3.0%造成悬浮物含量从150 mg/L降低至100 mg/L,当絮凝剂掺量为3.0%时,减水剂掺量从1.5%增加到2.5%造成悬浮物含量从约100 mg/L上升至110 mg/L。综合分析图3b、图3c可知,随着水泥掺量提升,悬浮物含量增加,3个关键因素对溶液悬浮物含量影响显著性大小依次为絮凝剂、水泥、减水剂,结果与方差分析吻合。
对比以上3组响应曲面图扭曲程度可知,絮凝剂和水泥掺量的交互作用造成悬浮物含量降低,对混凝土抗分散性有积极影响[14]。其余因素组合相互作用造成悬浮物含量增加,对混凝土抗分散性产生负面影响,但均不显著,结论符合方差分析结果。
3.3 抗压强度
通过拟合建立的水下不分散混凝土抗压强度预测模型为
Y3=+0.187 5PAM+0.175PC+0.987 5CM+
0.3PAM×PC+0.475PAM×CM-0.8PC×CM
-0.807 5PAM2-2.53PC2-0.957 5CM2+35.94
(4)
式中,Y3为抗压强度。
各关键因素对水下不分散混凝土抗分散性的影响规律如图4所示。
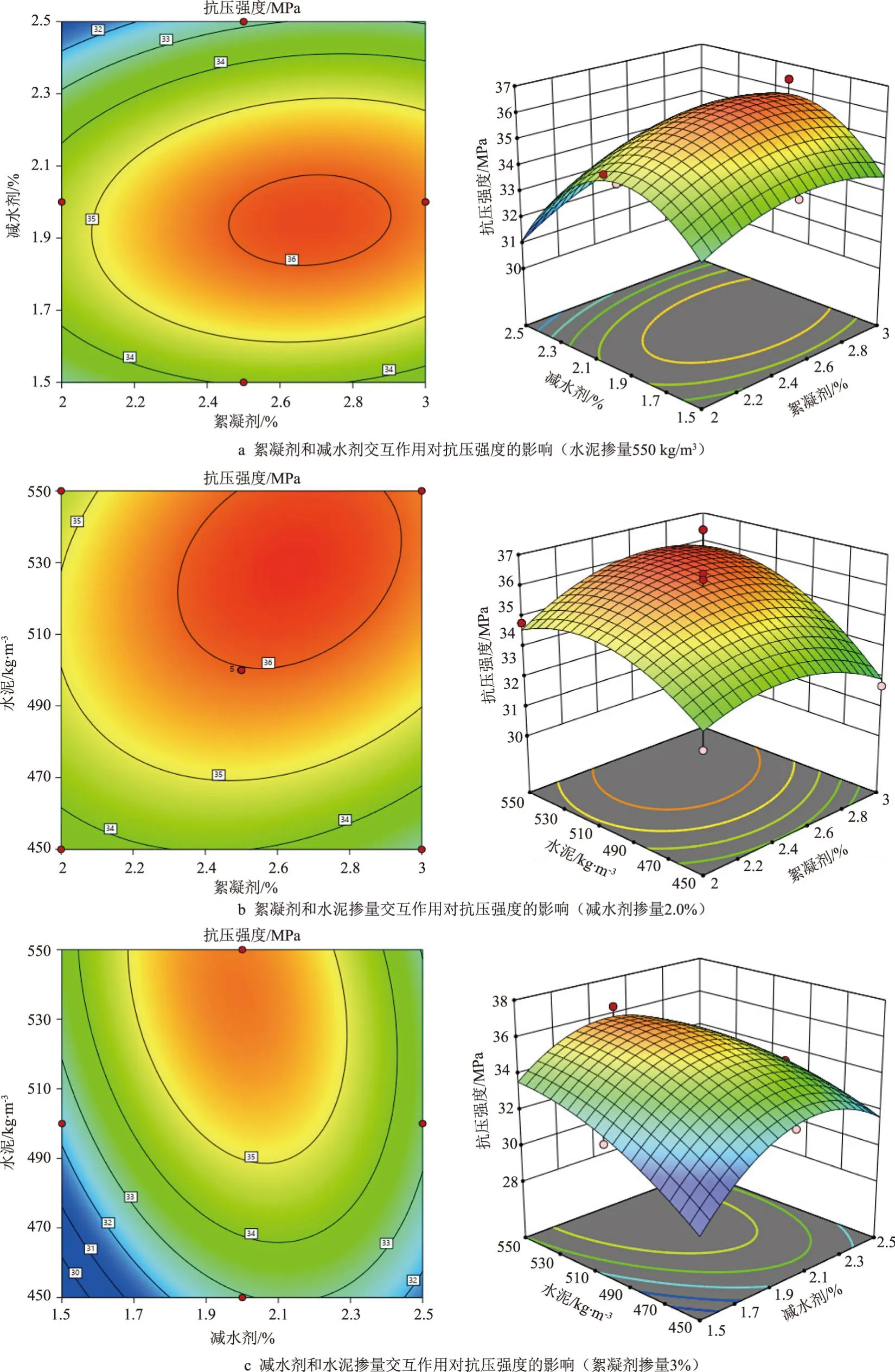
图4 三因素交互作用对混凝土抗压强度的影响
从图4可知,随着减水剂掺量的增加,混凝土强度明显呈先增大后减小的规律,当絮凝剂掺量为2.0%时,减水剂掺量从1.5%增长到2.5%造成混凝土强度从约34 MPa上升至约35 MPa再降低至约32 MPa。随着絮凝剂掺量的增加,混凝土强度呈现相似规律,但影响不大,当减水剂掺量为2.5%时,絮凝剂掺量从2.0%增长到3.0%混凝土强度从32 MPa提升至33 MPa左右。综合分析图4b、4c可知,随着水泥掺量提升,混凝土强度基本呈显著的上升趋势,3个关键因素对抗压强度影响显著性大小依次为水泥、絮凝剂、减水剂。由响应曲面图可看出,模型开口向下,在此试验设计范围内存在关于抗压强度的最优掺量。
等高线越近似于圆形,因素间的交互作用对混凝土的强度影响越小[15]。对比以上3组等高线图可知,减水剂和和水泥的交互作用对混凝土强度有负面影响,且较其他因素组合影响更加显著。其余因素组合相互作用均对混凝土抗压强度有利,但均不显著。
4 配合比优化结果
基于上述3个预测模型,设定坍落度达到220~240 mm范围内、悬浮物含量最小、抗压强度最大的条件,提出本试验条件下的最优配合比参数如表8所示。

表8 C30水下不分散混凝土推荐配合比
5 结 论
本研究通过响应面设计法建立了水下不分散混凝土絮凝剂掺量、减水剂掺量、水泥掺量关于工作性能、抗分散性能及抗压强度的预测模型,分析各因素对目标性能的影响及因素间交互作用,基于预测模型给出了混凝土的推荐配合比,主要得到的结论如下:
(1)基于响应面分析的试验设计法,分别建立了絮凝剂、减水剂、水泥掺量关于水下不分散混凝土工作性能、抗分散性能、力学性能的回归模型,各模型相关系数分别为0.891 5、0.939 0和0.887 0,模型的拟合效果良好,可用于水下不分散混凝土性能的预测。
(2)单因素对混凝土坍落度的影响显著,显著性的大小依次为水泥、减水剂、絮凝剂;单因素对混凝土溶液悬浮物含量的影响显著,显著性大小依次为絮凝剂、水泥、减水剂;单因素中水泥掺量对抗压强度的影响显著,其余因素不显著,显著性大小依次为水泥、絮凝剂、减水剂。
(3)各因素间的交互作用中,减水剂和水泥掺量对混凝土坍落度有显著有利影响;絮凝剂和水泥掺量对混凝土溶液悬浮物含量有显著有利影响;减水剂和水泥掺量对混凝土抗压强度有显著负面影响。
(4)根据预测模型提出了最佳的配合比选项供施工参考。

