空间六边形提篮拱安装线形算法研究

薛其林，王 吉，邱景奎

（1.桥梁智能与绿色建造全国重点实验室，湖北 武汉；2.中铁大桥科学研究院有限公司，湖北 武汉）

1 工程概况

宁波新典桥为下承式简支系杆异形拱桥，跨径213 m，西岸纵坡3%，东岸纵坡0.3%，变坡段设置R=1 500 m 竖曲线。桥宽42～56.2 m，矢高46 m，矢跨比1/4.63，拱脚到桥梁中心线的横向距离为17 m，拱轴线为1.7 次抛物线，两片拱肋向内倾斜16.928°形成提篮状。拱肋采用六边形封闭钢箱型，截面高度由拱脚5 m 渐变到拱顶3.5 m，拱肋宽度为3.0 m 不变，顶、底板厚40～48 mm，内部横隔板垂直于拱轴线布置，纵向布置加劲肋，主拱按照桥面中心线对称布置。主桥桥型布置如图1(a)所示。

图1 主桥桥型示意

主梁和拱肋在东岸进行拼装，拼装姿态为东西侧拱脚旋转至水平，拱肋共划分为15 个节段，为保证拱肋拼装角度的精确度，同编号节段同时在地面胎架以内倾16.928°的空间姿态进行拼装焊接工作。拱肋采用支架施工方法，将拼装完成的拱肋节段吊装到桥位支架上进行安装，西侧拱肋GL1～GL7 和东侧拱肋GL15～GL9 同步安装，拱肋GL8 为合龙段。拱肋节段划分如图1(b)所示。

相对于平面拱肋，空间结构复杂的六边形拱肋节段，在安装过程中，极易出现线形控制点与仪器不能通视或棱镜无法保持垂直等情况[1-2]。所以在安装过程中，随时存在重新做点的情况。对于大跨度拱桥拱肋节段数多，坐标计算极为复杂、计算量大，如果不能保证新做控制点坐标计算的时效性和准确性，则必然会影响拱肋合龙质量与进度。

该桥拱肋节段在现场拼装过程中，焊接量大，且处于空间倾角姿态，预制和拼装精度难以保证[3-5]。如果某节段因尺寸偏差或拼装线形误差，而无法安装到指定线形位置，此时需要计算出里程、偏距和高程的比例关系修正监控指令，使空间线形符合目标状态，从而减小对后续节段安装定位和焊接质量的影响。

针对上述问题，提出了一种复杂空间六边形提篮拱安装控制点坐标算法。本方法将实体结构转化为几何模型，实现控制点坐标计算参数化，能满足拱肋安装过程中新建控制点坐标计算的时效性和准确性；同时，针对拱肋加工过程中出现线形偏差的节段，通过输入偏差量计算出修正后姿态坐标，确保后续拱肋节段安装的空间线形符合目标状态。

2 拱肋预拱度计算

采用MIDAS/Civil 对整个施工过程进行模拟，计算拱肋在各施工阶段的位移变化，得到拱肋的预拱度值，计算模型如图2 所示。在拱轴线设计线形基础上，添加预拱度高度，推导出拱肋无应力状态[6-8]下的线形方程，继而确定添加预拱度后控制点的线形方程。

图2 全桥有限元模型

3 控制点空间坐标参数化算法

3.1 控制点参数设置

根据现场吊装条件，控制点布置于拱肋顶、底板位置，以拱肋分段线为参考，通过改变控制点位置参数L1、L2、L3的取值，实现对应控制点的坐标计算，各参数具体含义如下

L1：待安装拱肋节段上控制点到相邻分段线距离，为保证计算精度，L1取值介于100～300 mm 之间；L2：拱肋顶板控制点横向间距；L3：拱肋底板控制点横向间距。

控制点布置：控制点1 位于顶板中心线位置（箱口外），控制点2 位于底板中心线位置（箱口内）；控制点1n 和1w 分别位于桥梁中心线的内外侧，与测点1的距离均为L2；控制点2n 和2w 分别位于桥梁中心线的内外侧，与测点2 的距离均为L3；参数L2、L3同理。控制点3 与控制点1 布置同理。控制点布置如图3 所示。

图3 拱肋节段控制点布置

3.2 控制点安装坐标方程推导

将拱肋结构转化为几何模型，采用代数求解方法，推导出控制点的坐标方程，主拱按照桥梁中心线对称布置，为表述简洁，仅对X 负半轴左幅拱肋控制点的坐标推导过程进行详述。求解步骤为：拱轴线设计方程→控制点截面与拱轴线交点的坐标表达式→控制点1 的坐标方程→控制点1n 的坐标方程→控制点1w、2、2n、2w 的坐标方程→添加预拱度后的安装坐标方程。

拱肋构造坐标系统：X 轴表示里程，为桥面中心线，里程递增方向为正，原点位于主桥中心处；Z 轴表示高程，为竖直方向，向上为正；Y 轴表示偏距，垂直于X-Z 平面，向北为正。六边形提篮拱在XYZ坐标系下的拱轴线方程为式（1）：Y=b-Ztanβ。式中，f 为拱轴线的计算矢高；l 为计算跨径；β 为拱肋内倾角，即拱平面与竖直面夹角；b为拱脚到桥梁中心线的水平距离。

3.2.1 控制点截面与拱轴线交点坐标方程

控制点截面与拱轴线交点以C 点表示，将计算模型转换为几何模型：P 为拱肋节段分界面与拱轴线交点；B 为点P 在竖直平面上的投影点，D 为点B 在XY 平面上的投影点。C 点坐标计算几何模型如图4 所示。

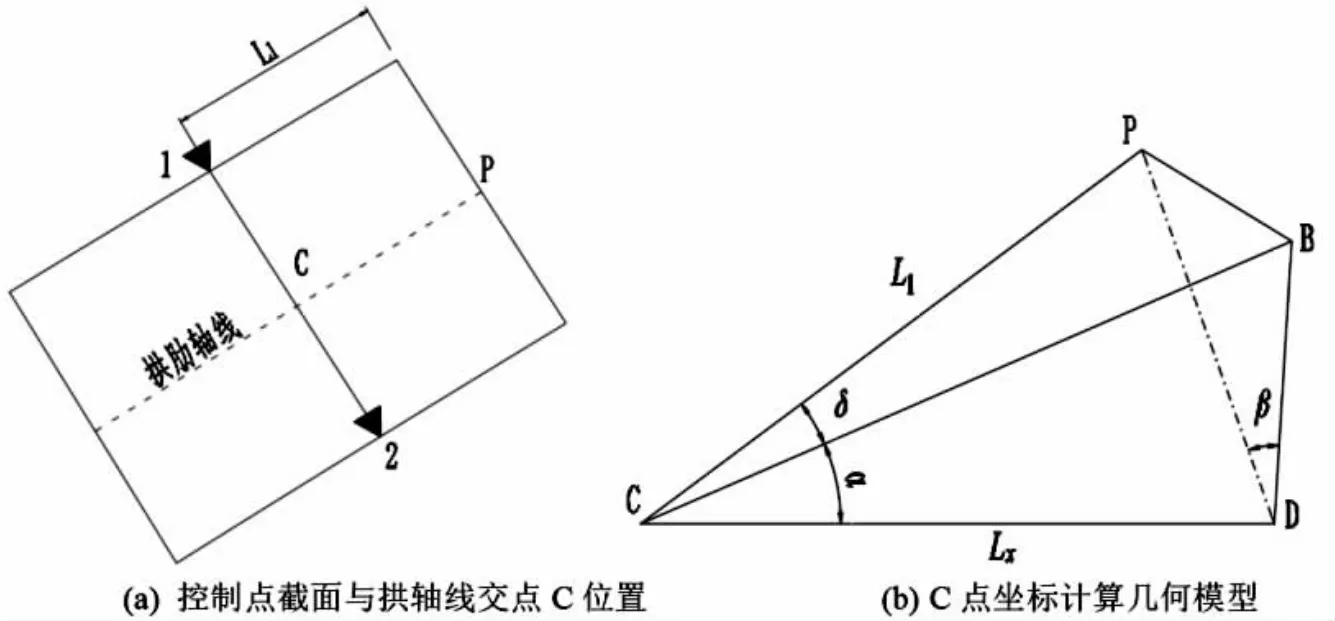
图4 C 点坐标计算模型

由图4 可知：∠PDB=β（拱肋内倾角），∠BCD=α（拱轴线在竖直平面内投影的切线角）。

每条分段线与拱轴线交点的里程已知，即XP坐标值给定。令∠PCB=δ，CD=LX，其中LX表示点P 到点C 的里程变化量，通过几何关系可得点C 的坐标方程式如下。

式（2）：

3.2.2 控制点1 的坐标推导

控制点1 用E 点表示，通过作辅助线将计算模型转换为几何模型，过E 点作平行于X 轴的直线，经过点F,使其满足EF⊥FC,作C 点到竖直平面的投影点G，连接CE、CG、CF、EF、EG、FG，控制点1 坐标计算几何模型如图5 所示。

图5 控制点1 坐标计算模型

图5(a)中，h1为点C 到控制点1 的直线距离,即拱肋截面高度的二分之一；h2为点C 到控制点2 的直线距离，若底板厚度为t，则h2=h1-t（拱肋各截面高度为设计已知量）。图5(b)中，△ECF 位于拱肋平面内，△EFG 位于竖直平面内，EF 为两平面交线。根据投影规律和直线与平面垂直的判定定理得，CG⊥FG,GF⊥FE；EC=h1，∠CFG=β，令∠ECF= γ，可得式（3）：

根据图5 中几何关系可得点C与控制点1 在XYZ 方向的变化量△xi=h1sinγ、△y1=h1cosγsinβ、△z1=h1coscγosβ，可得控制点1 坐标的具体表达式如下。

式（4）：

3.2.3 其它控制点的坐标推导

控制点1n 用H 点表示，通过作辅助线将计算模型转换为几何模型，控制点1n 坐标计算几何模型如图6 所示。

图6 控制点1n 坐标计算模型

图7 中，E H=L，∠MEH=β,通过几何关系可得控制点1n 坐标的具体表达式如下。

图7 拱肋线形测点布置

式（5）：

控制点1w、2、2 n、2w 的推导过程同上，此处不再赘述，在推导过程中注意对应的位置关系。

3.2.4 控制点安装坐标方程

经有限元计算分析确定主梁吊耳位置预拱度为零，为保证张拉吊杆时，主梁吊耳和拱肋吊耳处于同一平面，拱肋预拱度也沿着原拱肋平面添加。假设拱肋吊耳坐标为 (y,z)，预拱度添加值为Δhi，则添加预拱度后拱肋吊耳坐标为 (y-△htanβ,z+△h)。根据预拱度添加方式，在控制点坐标方程中YZ 方向添加预拱度值，即为拱肋节段安装坐标方程。

运用上述公式在Excel 中编制坐标曲线表格，通过改变拱肋节段控制点位置参数L1、L2、L3，实现各节段安装坐标的计算；若拱肋节段加工精度偏差，使安装节段的里程与目标值偏差±Δx，将式（2）中的XP替换为（XP±Δx），可实现偏距和高程的修正。

4 结果

4.1 安装计算精度分析

以西侧左幅拱肋节段GL1 为例，计算控制点1、1n、1w、2、2n、2w 的安装坐标。已知控制点位置参数L1=300 mm、L2=750 mm、L3=600 mm，GL1 分段线距离西侧拱脚水平距离8 444 mm，即XP=-98 063 mm，拱肋截面高h1=2 435 mm，底板厚度t=40 mm，各控制点处的预拱度均取Δh=3 mm。通过上述公式计算结果与拱肋三维放样模型中对应控制点的测量结果进行对比，如表1 所示。由表1 可知，最大偏差为2 mm，表明本方法计算精确度较高。

表1 控制点安装坐标精度分析

4.2 安装结果分析

每节段前端各1 个线形测点，如图7 所示。拱肋节段安装后，得到各测点轴线偏差、高程偏差、对称点高程偏差曲线，如图8 所示。由图可知，上游轴线偏差范围为-34～15 mm(负值表示轴线偏向下游)，高程偏差范围为-12～19 mm(负值表示高程偏低)；下游轴线偏差范围为-27～21 mm，高程偏差范围为-14～19 mm；对称点相对高程偏差范围为0～12 mm。依据《城市桥梁工程施工与质量验收规范》（CJJ-2-2008）要求：钢拱肋安装轴线允许偏差为±L/6 000 mm（取±35.5 mm），高程允许偏差为±L/3 000 mm（取±71 mm），对称点相对高程允许偏差为L/3 000 mm（取71 mm）。通过对比发现，所有测点均满足规范要求，且合龙后线形平顺。

图8 拱肋线形偏差曲线

5 结论

空间六边形提篮拱安装线形控制算法研究结论如下。

（1） 在无应力状态下，考虑拱肋成桥设计线形和有限元计算得到的预拱度值，将空间拱肋结构转化为几何模型，提出了一种复杂空间六边形提篮拱安装控制点坐标参数化算法。

（2） 通过工程实例计算结果表明，该算法精度较高；同时通过合龙后线形测量结果发现，本方法有效地解决了拱肋安装过程中新建控制点坐标计算的时效性和准确性。

（3） 针对加工中出现精度偏差的节段，通过输入里程偏差量，计算出目标状态下的偏距和高程，以此修正安装指令，确保了安装节段和后续节段线形处于目标姿态，使得合龙后拱肋线形平顺且满足设计要求。