Matlab 环境下拖拽式焊接机器人的运动学仿真实验

才 洋 于功志

（大连海洋大学，辽宁 大连 116023）

焊接机器人是时代发展的趋势，是“中国制造2025”和“工业 4.0”的重要研究领域，在工业应用中占比52.8%以上，被誉为“制造业皇冠顶端的明珠”和“工业的裁缝”[1]，从小型家具到航空航天的尖端产品都有其大规模应用身影。根据 IFR 的报告，我国已成为全球最大的机器人市场，占有量达33%，世界传统制造业也将从大批量单一化生产向小批量多元化生产转型[2]，生产设备安全性需求将进一步提高。同时，制造业还将面临高级技术工人的严重短缺问题，其中造船业90% 的工作仍依赖于人力。但它的出现有效解决了人口红利不足、供需关系失衡、劳动密集型企业用工难、人力技术不济等问题，使“一人一工位”的传统模式逐渐转变为“一人一条线”的智能制造模式。其多项核心技术广泛应用于制造业，仿真技术经过多阶段多层次的发展，已可从不同角度进行应用。

迄今为止，不同种类与构型的机器人应用各式的设计和分析求解方法，如邢红辉等[3]、冷玉珊等[4]对串联机器人完成了运动学仿真分析；程堂灿等[5]、薛良豪等[6]、黄旭楠等[7]均对特定型号与构型的焊接机器人进行了运动特性分析和轨迹规划，在分析中他们均采用了运动学D-H 建模法，在求解上分别采用了迭代法、数值法与结合算法，对机械臂本体模型、运动轨迹、运动性能进行验证分析并得出结论；朱志明[8]利用蒙特卡洛法求解了焊接机器人的工作空间；宫成[9]完成了矿用智能遥控搬运拖拽机器人研发；杨恺等[10]设计了一种巡线机器人，通过Matlab 仿真分析验证了该机器人的合理性。

但目前此类拖拽式焊接机器人缺乏完整的仿真分析与实验方案，现基于Matlab 对该机械臂进行完整的运动学分析，即MDH 参数建模、正逆运动学分析求解、模型验证、轨迹规划和工作空间分析。综上所述，仿真技术作为机械臂核心技术中的重要保障与前提，对其制订实验方案是必要的。

1 机械臂工作流程与仿真

当前示教方式包括拖拽示教、遥控示教及示教盒示教，该型号机器人可在智能编程的基础上结合拖拽示教。在实际生产中，拖拽示教具有操作简单、灵活、高效、安全等优点，能够在短时间内完成复杂任务，结合智能编程提升生产能力。该实验对机械臂的运动方程进行分析求解，即处理运动学方程的表示与求解问题，分析求解过程中忽略外力的影响，最终获取机械臂关节中心点与大地坐标系之间的位姿映衬关系，求解末端执行器与大地坐标系的运动学参数信息。

1.1 工作流程

拖拽式焊接机器人支持通过拖拽控制器移动示教，其系统内部的工作流程包括感知、规划、控制和反馈等，拖动后各关节编码器记录位置信息，形成轨迹数据并储存在计算机中。下次启动时，在电机的运转下机械臂关节轴会依次经过先前采集点，完成轨迹再现[11]。

工作前首先确保机械臂与工作总站处于安全状态，其次检查整体软硬件的连接，如通信与机械安装，然后选择加工程序、调配技术参数，结合自动编程选择拖拽示教。实验开始前可选择仿真分析与焊接模拟，前置工作准备完成后启动自动焊接模式。实际生产中可根据需求采取机械臂工作模式下的策略、算法与数据库，针对不同工况进行轨迹扫描与焊接工艺的选择。最后检查焊缝质量与焊接轨迹，将机械臂手动拖拽或自动回零，关闭电源清理工作区域，进行后续处理。具体工作示意如图1 所示。

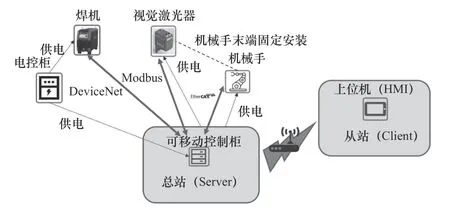
图1 拖拽式焊接机器人工作示意图

1.2 机械臂的构成

该拖拽式焊接机器人的构成主要包括基座（控制工程机）、机器人上下臂、关节模组（J1～J6轴）、末端工具法兰、通讯与电源电缆、拖拽控制器。机械臂各关节轴中都配有独立的伺服电机和编码器。图2 为拖拽式焊接机器人结构图。

图2 拖拽式焊接机器人结构图

1.3 运动学模型的构建

针对该拖拽式焊接机器人使用改进DH（Denavit-Hartenberg）建模法建立运动学模型，该拖拽式焊接机器人的DH 参数见表1。建立过程中使大地坐标与笛卡尔坐标重合，建立的坐标系模型如图3 所示。

表1 拖拽式焊接机器人DH 参数表

图3 拖拽式焊接机器人D-H 模型图

在拖拽式焊接机器人各轴心上建立坐标系，分析各轴间坐标系变化关系，通过矩阵进行表达与计算，得到基座到末端关节轴的总位姿矩阵。

2 运动学的分析求解与验证

拖拽式焊接机器人运动学包含正、逆运动学两方面，其本体为较复杂的非线性系统。在分析求解时，关节参数计算和运动学方程的推导较为繁琐，其中分析求解可采用代数法、分离变量法、几何法和迭代法等。该实验采用迭代法求解，具体流程如图4 所示。

图4 运动学分析求解流程图

2.1 正运动学分析求解

求运动学正解是在已知拖拽式焊接机器人的DH 参数与关节结构参数情况下，求解关节末端执行器对应的大地坐标系的位姿、速度、加速度等运动学参数。对其建立运动方程，又称为机器人的运动分析。零点基坐标系与关节末端坐标系之间的转换过程，用矩阵T表达：

式 中：Rot(z,θi)和Rot(x,αi)分别表示绕Z轴、X轴旋转一定关节角度的变换矩阵；Trans(z,di)和Trans(x,αi)分别表示沿Z轴、X轴平移一定位置量的变换矩阵。

展开式（1）得：

齐次变换矩阵如下：

将齐次变换矩阵连乘得到如下矩阵：

式中：px、py、pz为空间向量，表示机器人在空间中X、Y、Z三轴位置形成的空间坐标点。代入机器人关节信息，对以上正运动学分析式展开求解，可求得唯一解。

式（5）和式（6）为化简应用和角公式：

根据给出的D-H 参数，运用Matlab 得出T矩阵表达式，这里设d1=D1，a3=A2，d4=D2，d6=D3。其中 Si=sinθi，Ci=cosθi。式（4）中计算结果如下：

将机械臂D-H 参数表中关节变量值导入式（4），求得结果如下：

如图5 所示，将X、Y、Z值对照运动学正解第四列结果进行对比，可见与之完全吻合。针对该关节变量值与位姿，现场结合拖拽示教与编程示教验证了拖拽式焊接机器人正运动学求解的正确性。

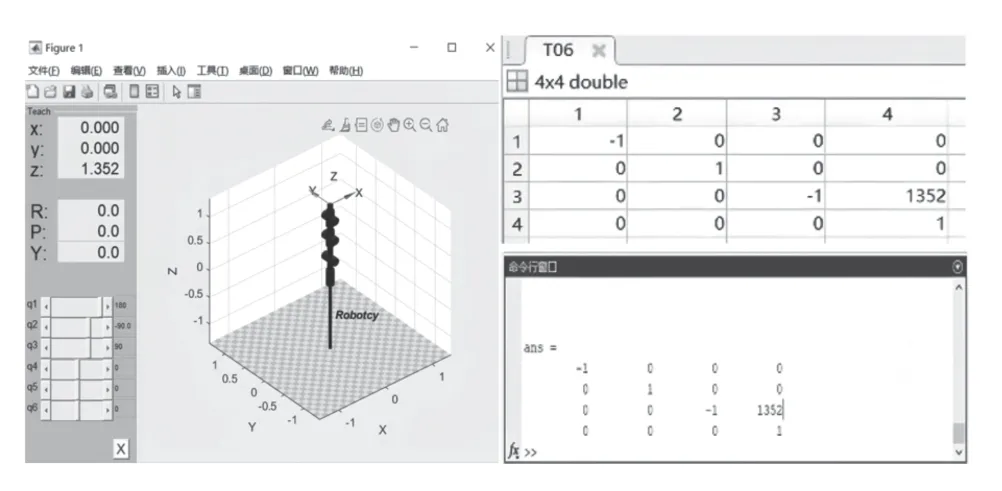
图5 关节模型与变量图

2.2 逆运动学求解

对拖拽式焊接机器人求逆解，即在已给定其几何参数与对应参考坐标系下预期位姿时，求解本体可达的关节变量，又称为机器人运动的综合。该部分采用牛顿-拉夫逊迭代法，限制实验初始值求解非线性方程，运用函数计算雅可比，不断进行迭代直至收敛。该方法具备求解连续且快速的优点，具体过程如下。

首先建立运动学非线性方程组：

式中：f(x) 表示机械臂正向运动学，Pd表示末端执行器期望位姿。

假设r为F(x)=0 的根，选取x0为r的初始近似值，通 过点 (x0,f(x0)) 作曲线y=f(x)的切线L，切 线与x轴存在交点，得到切线方程：

求出切线L与x轴的交点x1，以此类推，不断求出切线L与x轴的交点直到无限接近于0，得到第k次的迭代公式为

式中：F′(xk)表示方程的雅可比矩阵。

在Matlab 中定义最大迭代步数与误差阈值，定义当前关节角度为迭代起始角，得到非线性十二维单解方程组，即误差方程组。运行迭代，得到雅可比F′(xk)，据式（14）推算出下一关节角度，并更新非线性方程，判断达到最大迭代次数后退出while 循环，求出逆运动学最优关节角度。变换后的式（4）表达如下：

以上利用牛顿-拉夫逊迭代公式求解机械臂逆运动学，也可利用SVD 形式求解，它是一种求非方阵伪逆的计算方法。

通过运算得到的关节弧度与机械臂位姿经现场拖拽示教验证，到达位姿与点位信息同计算结果完全一致。

2.3 运动学模型验证

该部分选取了 3组实验数据对拖拽式焊接机器人运动学算法的准确性进行验证，3组实验数据分别 为[π/3,π/2,0,0,0,0]、[π/3,π/2,π/4,π/4,π/6,0]、[π/4,π/6,π/3,π/3,0,π/6]。实验中采取了两种方式，其一为打开机械臂的自动模式，输入期望关节角，手持并启动拖拽器，协同拖动多关节轴与末端执行器使机械臂到达预期位姿；其二为调用上位机与机械臂通讯，采用编程控制与示教器示教工作。两种方式均将位姿信息作为输入，输出运动学逆解，取得验证结果一致，但拖拽示教在保持精度的同时节约了近一半的工作时间，且大大降低了操作难度。计算得出机械臂姿态，如图6～图8 所示，位姿矩阵与逆解最优值为

图6 姿态1

图7 姿态2

图8 姿态3

对三组实验数据完成了核算，保障了机械臂关节数据的有效性，进一步验证了计算的正确性。

3 空间轨迹规划与仿真

实验分别采用了三次插值轨迹规划算法与五次插值轨迹规划算法，并且基于对速度与加速度的调节机制进一步对轨迹进行分析、差分与优化。具体流程图如图9 所示。

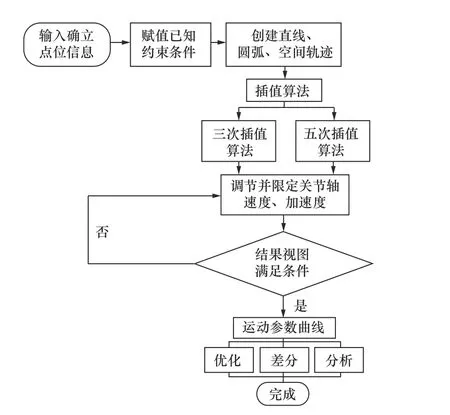
图9 轨迹规划流程图

3.1 五次插值轨迹规划

实验中将机器人初始点与终止点的位置、关节角速度、关节角加速度作为限制条件，根据限制条件的数量使用五次插值轨迹规划方法，配合限制角速度与角加速度的调节策略，限定的范围见表2。

表2 五次插值方法参数限定表

将机器人模拟时间设为2 s，起始与终止角速度为0，起始点(-200,200,-50)，引导点(-150,100,-100)，终止点(-200,-50,75)，采样点个数50。初始点关节值(2.317 1,2.317 1,2.488 8,-1.621 9,-2.218 4,0)，终止点关节值(-0.220 2,-0.220 2,2.066 5,-0.161 3,2.796 1,0)。采用五次多项式插值，函数表达式如下：

式中 ：v0为起始点关节速度；v1为终止点关节速度；a0为起始点关节加速度；a1为终止点关节加速度；T=t1-t0；h=q1-θ0，其中 θ0为起始点关节角度，q1为终止点关节角度。

图10 包括机械臂运动轨迹图、各关节轴运动性能曲线图和机械臂模型图，验证了五次插值轨迹规划方法的优越性。根据其中参数条件，拖拽式焊接机器人可达到一个连续且稳定的工作状态。经规划后提升了机械臂的操作空间，进而保障了其工作质量与效率，降低了故障率与危险发生率。

图10 五次插值效果图

3.2 三次插值轨迹规划

三次插值轨迹规划方法同样适用于机械臂的轨迹规划，采取调节策略，相关参数限定见表3。

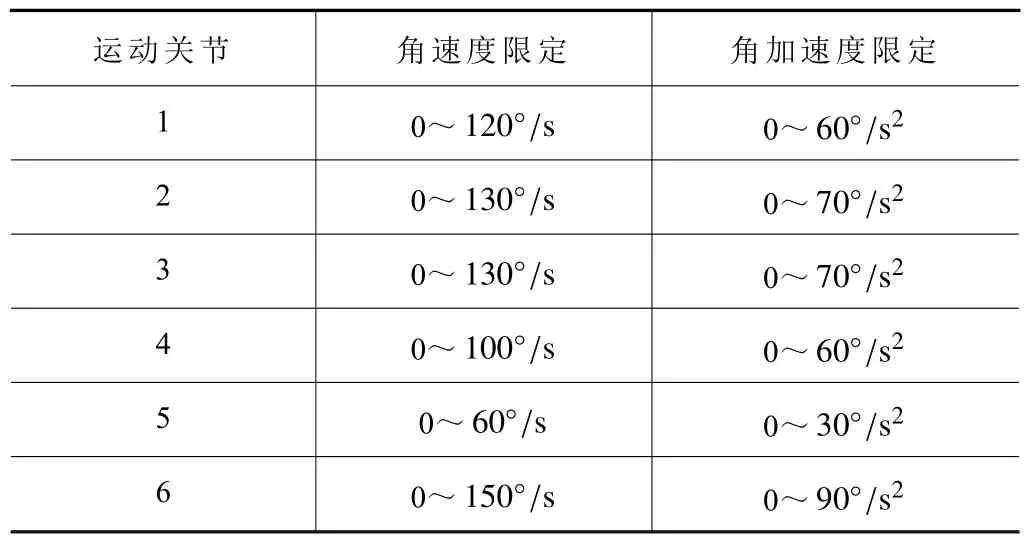
表3 三次插值方法参数限定表

预实现单关节轴的平稳运行，应用三次插值轨迹规划，函数表达式如下：

式中：v0为起始点关节速度，v1为终止点关节速度，T=t1-t0，h=q1-θ0，q0为起始点关节角度，q1为终止点关节角度。经运行，效果图如图11 所示。

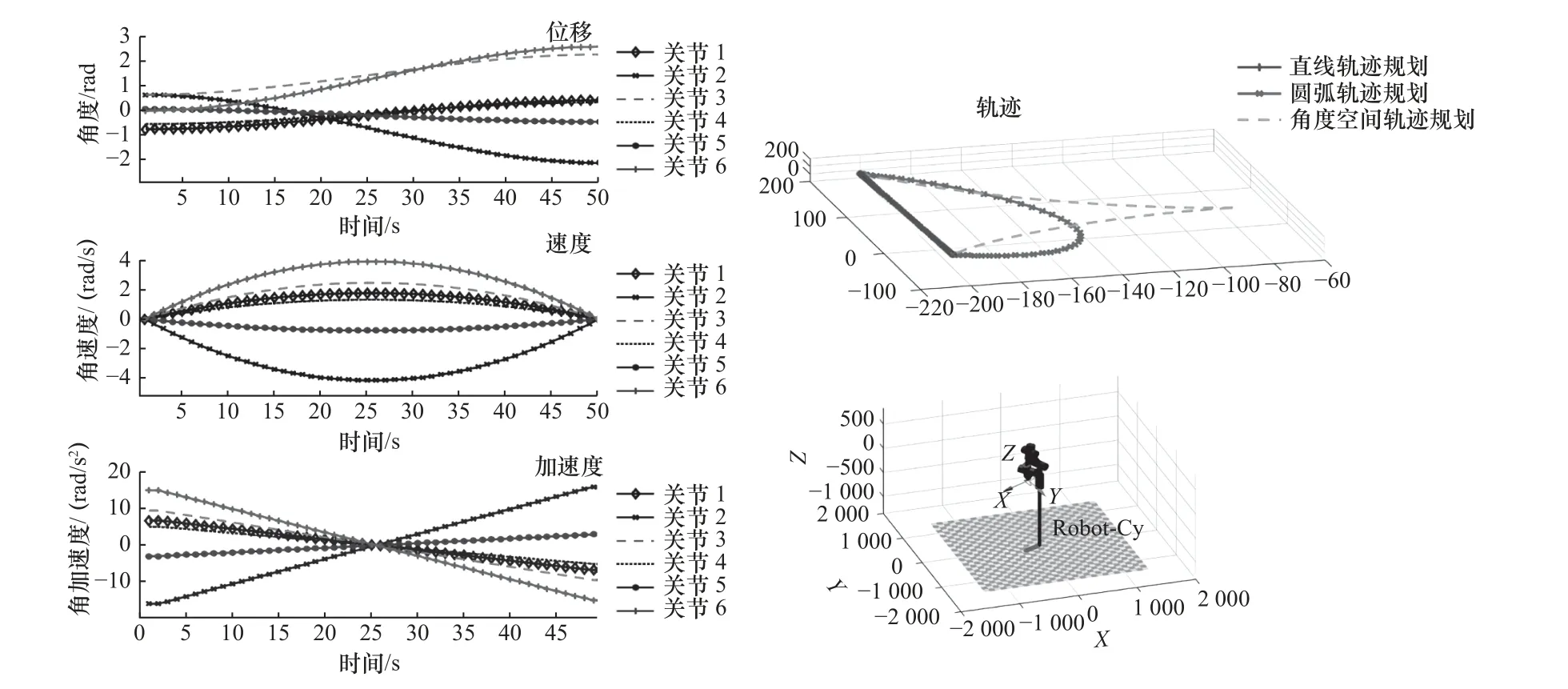
图11 三次插值效果图

4 工作空间分析

求解工作空间的方法主要有数值法、图解法和解析法三类，相比于其他方法，数值法求解方便且直观，推算准确性好，不需要额外考虑机器人避碰等干扰问题，并省去了复杂且直观性不强的数学模型分析求解。该部分采用蒙特卡洛法对工作空间进行求解。

4.1 蒙特卡洛法

蒙特卡洛（Monte Carlo）法作为一种重要的数值计算方法，其核心思想包括对问题的定义、采样方法的选择、目标函数计算方法的选取、评估采样点的数量定义、工作空间的更新求解、终止条件的判断，最终输出反映实际情况的最优数值解，生成工作点云图。该方法可自由控制计算精度与计算资源的平衡，实现加速求解，其自身具有灵敏度高、适用范围大、高度并行化的特点。求解前可巧妙地规避问题的产生，处理高维问题优势显著，不受维度问题影响。运用时需对关节变量范围进行限定，对样本点数目进行综合考量后选取，机械臂遍历取值后生成正运动学方程解的空间向量集合，绘制点云形式的工作空间视图。工作流程如图12 所示。

图12 工作空间分析流程图

4.2 蒙特卡洛法全局分析求解

首先由拖拽式焊接机器人正运动学方程得到其终端执行器的空间位置向量。由式（4）终端位姿矩阵求得位置向量为

设置取点数为N=5 000，在Matlab 环境下调用Rand 函数定义(0,1)的均匀随机数，生成随机步长L：

随机变量为

将式（25）求得的机械臂各关节变量随机值代入正运动学方程求解，求得机械臂终端执行器在笛卡尔坐标系下的位置向量。设置迭代次数，按照采样次数重复执行步骤，直到达到随机样本最大值，Matlab 根据点的收集形式输出机械臂工作空间点云图。

求解工作空间点云图，XOY、YOZ、XOZ三个截面投影如图13 所示。坐标轴轴向点云极限尺寸见表4。

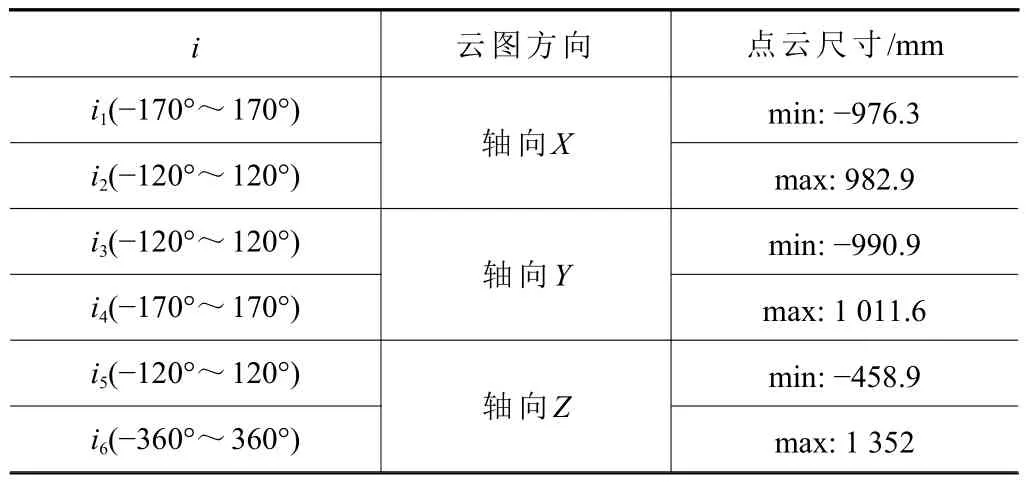
表4 拖拽焊接机器人全局点云尺寸表

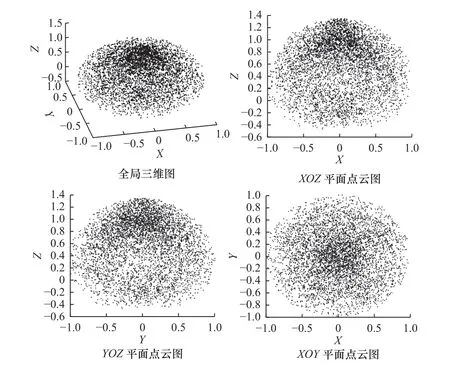
图13 全局点云视图

4.3 蒙特卡洛法限定分析求解

为了实验更符合需求，在满足焊接条件的同时缩短生产时间、提升生产性能、减少无效或重复空间占用，进行如下限定工作空间的分析求解。该部分采用拖拽示教扫描履遍工况信息，并结合编程与示教器示教对扫描后的工况进行二次检查，拖拽过程中数据均实时精准地反馈至上位机。工况由底板、面板、腹板、立板、肘板、补板组成，单位均为mm，板厚均为10 mm，详细尺寸如图14 所示。

加装工具焊枪与视觉模组后进行实验，所涉用具如图15～图17 所示。

图15 机械臂加装实验图

图16 加装工具模型图

图17 拖拽器功能与构型图

如图15 所示，以工况左端点为零点坐标轴右端与上端为正方向。拖拽式焊接机器人具体实验工作位姿与坐标点信息见表5。

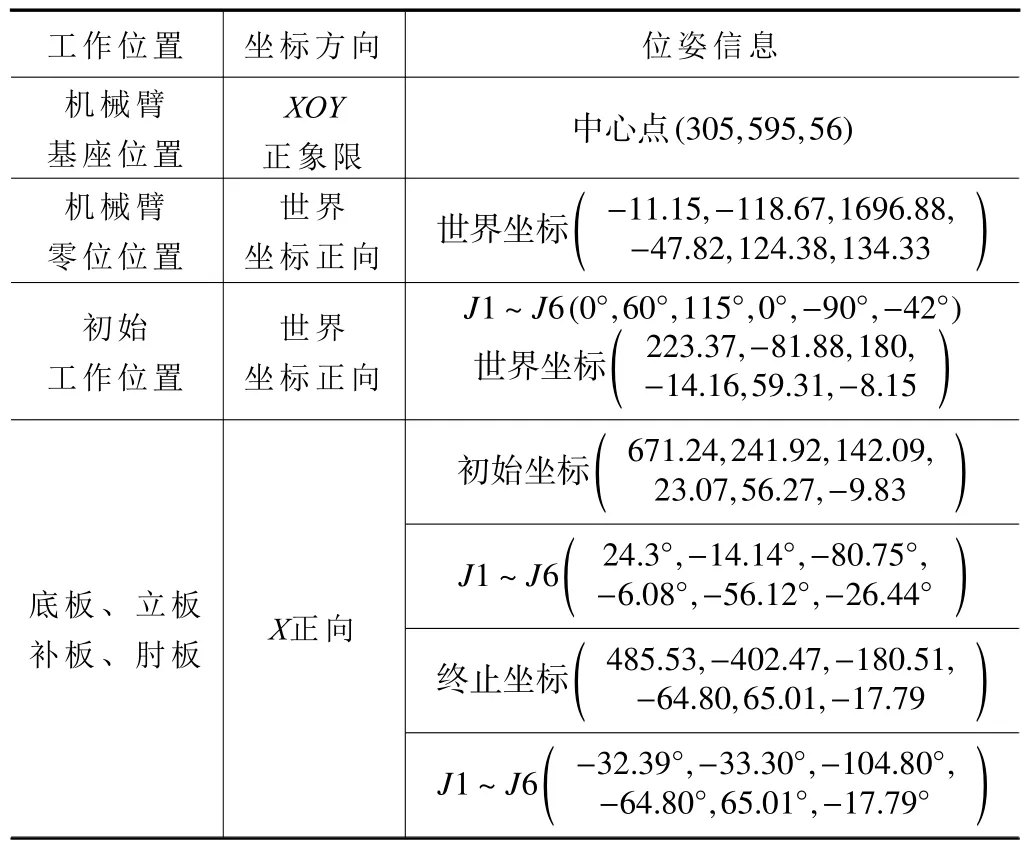
表5 机械臂实验信息表

综上，实验得到了最适宜的方案，机械臂到达工作起始点后将各轴旋转极限限定，限定点云视图如图18 所示，坐标轴向点云极限尺寸见表6。

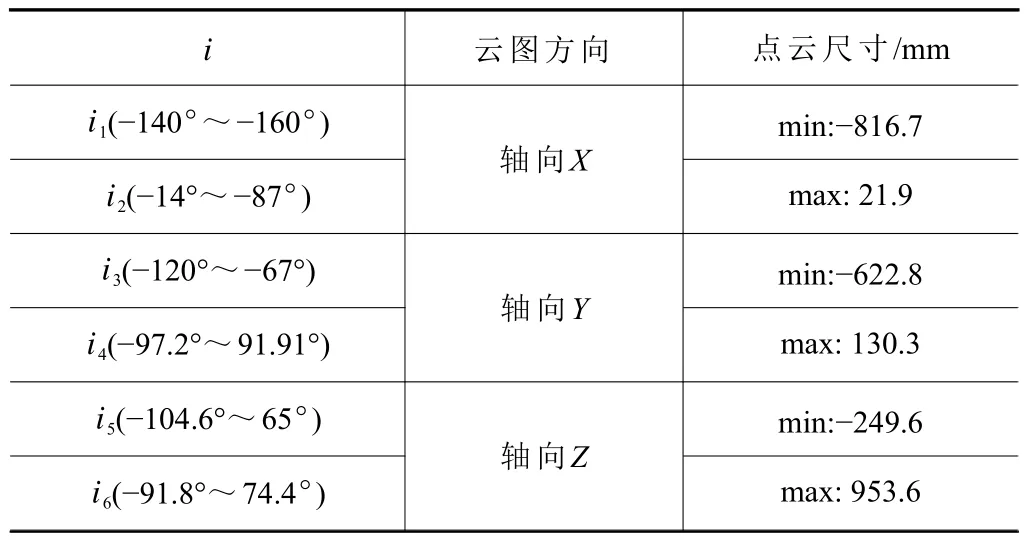
表6 拖拽式焊接机器人限定点云尺寸表

图18 限定点云视图

5 结语

该实验基于Matlab 使用改进DH 法建系，完成了对拖拽式焊接机器人的运动学建模验证、分析求解、轨迹规划、工作空间分析求解。实验过程中大地坐标与笛卡尔坐标重合，使用ZYX的欧拉角表现形式，得到了关节末端位姿与各关节角间的映衬关系。实验结果充分证明了拖拽式焊接机器人的合理与稳定。

该实验为后续研究和实际工作提供了理论基础与重要数据支持。结合该实验方案使用编程技术与拖拽示教，可事半功倍地解决实际问题。此工作方式兼备智能化与自动化的同时，达成了提升生产性能的最终目的，在减少产品成本消耗与缩短制造周期上产生积极影响。可基于该实验方法验证并开发相应算法、系统及更具智能和柔性的机械臂，在实际应用中可将拖拽式焊接机器人的装置拓展，从技术、系统及种类等方面，以不同形式应用在多行业环境中。