4+2 自由度叶片抛磨专用机器人轨迹规划方法研究*

任利娟 陈 恪 闫伟健 李 堃 杨志坚 张广鹏

（①西安理工大学机械与精密仪器工程学院，陕西 西安 710048；②秦川机床工具集团有限公司，陕西 宝鸡 721000）

叶片作为透平机、航空发动机等动力设备的核心零件[1]，其加工质量直接影响其服役性能和寿命。抛磨作为叶片尺寸加工的最后一道工序，对其最终的形状精度有重要的影响。目前，叶片自动化抛磨主要有机器人抛磨[2-3]和机床抛磨[4]两大类。机床抛磨叶片具有加工精度高、产品质量稳定、技术较成熟等优点，但其柔性和可扩展性一般；机器人抛磨叶片具有工作空间大、运动灵活、可拓展性强、性价比高等优势，在叶片抛磨加工中得到越来越多的关注和应用。

机器人砂带抛磨时，需要规划好机器人末端运动轨迹，轨迹规划的精度直接影响到了抛磨产品的质量。目前，叶片抛磨机器人轨迹规划方法是通过离线编程方法设计机器人在空间的运动轨迹。离线轨迹生成的基本步骤是[5-8]：首先基于三维扫描数据通过逆向工程建立叶片的三维模型；然后将三维模型导入专业的CAM 软件，通过编写一定的算法，结合加工工艺参数要求和叶片特征信息，生成叶片加工轨迹信息；最后通过叶片轨迹信息指导加工装备抛磨叶片，在抛磨期间再辅以力-位控制，对叶片轨迹信息进行修正，最终完成叶片抛磨作业。屈展等[9]在传统的逆向工程的基础上添加了交点追踪优化算法，提高了叶片建模的完整度和轨迹规划精度；Liang X F 等[10]利用点云切片算法和交集法创建初步接触点集，使得生成的轨迹能更好地顺应叶片型面的曲率变化，保证加工过程中线速度的稳定。

目前机器人抛磨叶片多采用串联式6 自由度机器人[11-12]，其多关节串联导致的弱刚性问题直接影响了大型叶片抛磨精度和效率。本文自主设计研发的4+2 自由度叶片抛磨的专用机器人[13]，通过将2个自由度分配到抛磨工具端，缩短了串联传动链，提高机器人夹持叶片的抗变形能力，本文主要开展适用于该机器人的叶片高精度抛磨轨迹规划方法研究，为该机器人系统用于叶片高精度抛磨提供理论和技术支持。

1 4+2 自由度机器人结构及运动原理

叶片作为典型复杂曲面零件，机器自动化磨削需要至少6 个运动自由度，基于模块化设计的思想，本文自主研发设计的叶片抛磨专用机器人将传统的6 自由度串联结构拆分成四自由度叶片运动单元和2 自由度叶片抛磨单元。运动单元负责叶片的装夹和进给动作，抛磨单元负责调整抛磨工具的姿态以适应叶片曲率的变化，两个单元协同工作，共同完成叶片表面的抛磨作业[13]。

叶片抛磨专用机器人系统结构如图1 所示，4自由度叶片运动单元包括一个由丝杠导轨副组成的沿Z轴的直线移动自由度和3 个绕其平行轴的回转运动自由度；叶片抛磨单元则包括绕X轴和绕Y轴的回转运动，同时气缸可提供沿Y轴的法向力控制。

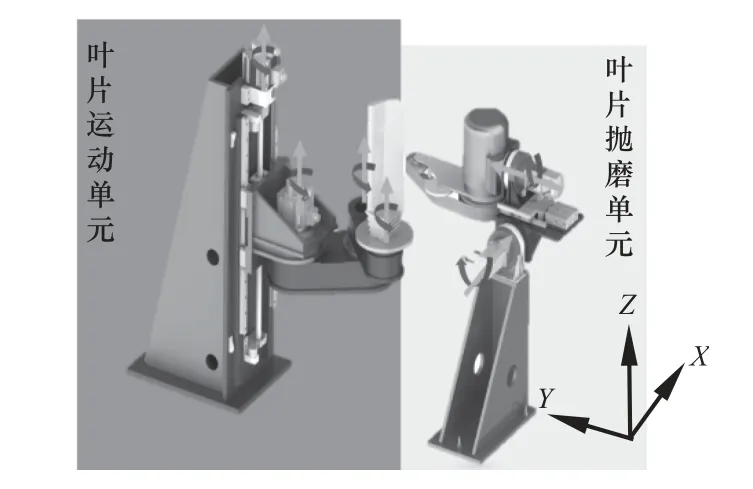
图1 4+2 自由度专用叶片抛磨机器人系统

1.1 4 自由度叶片夹持单元

4 自由度叶片运动单元主要部件如图2 所示，在结构上4 自由度叶片运动单元包含一个直线运动关节和3 个旋转运动关节。考虑到末端存在较大负载，将第一个关节设计为滚珠丝杆直线运动关节，叶片置于关节四的工作台上，通过工作台上的销轴完成定位；关节二和三组合运动，使叶片可以在X Y平面内运动；关节四带动叶片沿着C轴旋转。

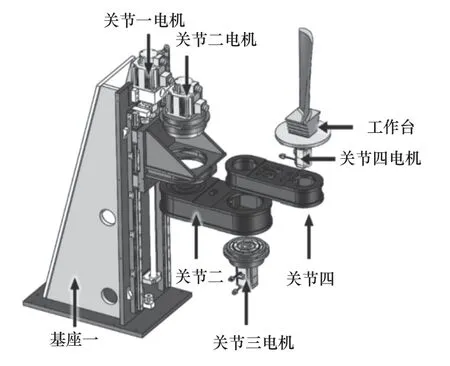
图2 4 自由度叶片夹持单元

1.2 2 自由度砂带抛磨单元

2 自由度叶片抛磨单元主要部件如图3 所示，该单元由2 个旋转关节组成，分别控制抛磨砂带机的俯仰与翻滚姿态。第六个关节安装在气缸驱动的滑块上，可以实现法向磨削力的在线调整，与运动轨迹协同实现叶片的自适应抛磨加工。砂带磨削机构由三向异步电机驱动驱动轮，带动砂带进行高速运动，张紧轮为砂带提供张紧力，接触轮为柔性橡胶材料。

图3 2 自由度砂带抛磨单元

2 机器人运动学模型

本文设计的叶片抛磨专用机器人由2 个单元组成，基准坐标系定义在机器人运动单元丝杠轴线与底面相交处记为Σ0，抛磨单元的基坐标系定义在基座上，坐标系原点在五六关节轴线公垂线与底面相交点处，记为ΣA，定义在机器人关节i上的坐标系称为坐标系Σi，如图4 所示。

2.1 运动学正解

本文基于D-H 法建立的机器人运动学模型，机器人的任意两相邻连杆的位姿关系都可以由4 个参数ai-1、αi-1、di、θi来表示。其中ai-1表示从zi-1到zi沿xi-1偏移的距离；di表示从xi-1到xi沿zi偏移的距离；αi-1表示从zi-1到zi以xi-1为轴旋转的角度；θi表示从xi-1到xi以zi为轴旋转的角度，αi-1和 θi数值通过右手规则确定。机器人相邻关节坐标系的齐次变换矩阵可由D-H 法得出：

根据式（1），顺序连乘对各个变换矩阵可以求得第四关节末端中心相对于运动单元基坐标系Σ0 的变换矩阵：

式中：符号具体表达式见表1，其中c 为cos，s 为sin，1、2、3、4 为第一到第四关节的坐标系沿z轴的转角，c1,2,3和cθ1,2,3是cos(θ1+θ2+θ3)的缩写，其他类似。ψp和θp为第五和第六关节分别沿X轴和Y轴的转角，p表示沿下标轴方向的位移。

表1 式（2）中各符号表达式

同理可求得叶片抛磨单元接触轮中心相对于基坐标系ΣA的变换矩阵：

2.2 机器人运动学逆解

本文采用解析法进行机器人运动学逆解的求解，通过建立本文特定结构机器人的数学模型，获得机器人末端位姿与关节变量之间的关系。首先对于运动单元部分求逆解，假设末端工作平台圆心此时坐标为(x4,y4,z4)，工作平台此时想要抵达的位姿角为θ，如图5 所示。

图5 关节角度变换

根据余弦定理可得：

当 s3>0，运动单元处于右手系；当 s3<0，运动单元处于左手系；当 s3=0，运动单元处于奇异解位置，则θ3为

θ2可被表示为

式中：

θ4可被表示为

本文设计的机器人运动单元第一个关节使用滚珠丝杠传动，因此关节一的关节变量可用θ1表示：

式中：Ph为滚珠丝杠导程，本文取10 mm。

然后对抛磨单元进行运动学逆解。抛磨单元的主要功能是调节砂带机相对于叶片的俯仰角和翻滚角，若要求砂带机的姿态为(ψb,φb)，则θ5和θ6可被表示为

机器人的运动学逆解即式（5）～式（9），机器人在实际工作中，各个关节都受结构限制，因此解的个数是有限制的，本文在选择运动学逆解时，按照关节欧式距离最小原则，使机器人末端执行器按照最短路径运动。

式中：θi为当前位姿对应的关节参数，（°）；θni为目标位姿对应的关节参数，（°）。

3 叶片抛磨轨迹规划

图6 所示为本文的叶片三维模型，为了防止接触轮与叶片曲率干涉，本文选用水平加工方式生成叶片抛磨轨迹，通过控制刀轨的残留高度误差，获得叶片表面的一系列刀轨。本文通过截面法获得基础的刀路、通过参数线法根据加工余量偏移生成完整的叶片抛磨加工的刀位文件。假设砂带机接触轮上的砂带宽度为b，刀路轨迹行距按照2/3～3/4 倍的砂带宽度以保证刀路重叠，降低残留高度。

图6 截面法

机器人依靠末端刀具将圆弧细分为直线逼近运动来完成曲线加工，对抛磨加工而言，首先把待抛磨轨迹曲线离散为一组位置与时间对应的插补点，然后用一组线段依次连接插补点来拟合曲线形状，如图7 所示。直线段与理想曲线之间的误差称为逼近误差，误差一般与插补步长负相关。若步长过小，插补点的数量过密，会严重拖累程序处理效率。较大的步长虽然使抛磨效率提高，不能保证加工精度要求。因此加工步长的选择应当综合考虑曲面的误差要求和加工效率。

本文设计的机器人使用数控加工中常使用的NC 数控语言做控制指令，因此，需要将CLSF 文件转换为常见的G 代码格式。刀位文件定义的刀轴矢量示意如图8 所示。

在本文的数控系统中，i、j、k与机器人的位姿角存在以下关系：

x、y、z是叶片坐标系下的刀位文件坐标数值，与NC 代码中x、y、z的转换关系由数控系统的设计确定，为方便计算，令(x,y,-z)=(X,Y,Z)。

通过上述关系，可以将刀位文件中的(x,y,z,i,j,k)转换为NC 代码，供机器人控制系统使用。

4 运动单元和抛磨单元协同运动模型

基于上文获取的叶片型面曲线，本节将建立运动单元和抛磨单元协同运动模型，使两个单元协同运动共同完成叶片的抛磨任务。

运动单元和抛磨单元要想实现协同抛磨作业需要满足3 个条件：

（1）假设在基坐标系下紧贴在张紧轮的砂带外表面有一点(Bx,By,Bz)，这一点位于砂带机端部位置。在第四关节的初始坐标系下，叶片表面待抛磨点为(Px,Py,Pz)。在抛磨过程中点B和点P应当保持接触状态，即(Bx,By,Bz)=(Px,Py,Pz)。

（2）接触轮中心轴线与待抛磨点法矢量正交，由于实际操作中，接触轮中心轴线表达比较困难，可以使用始终垂直于接触轮中心轴线的第六关节轴线代替，只要保证第六关节轴线与待抛磨点法矢量平行即可。

（3）由于本文采用叶片横截面型线作为加工的引导线，因此在抛磨过程中需要使接触轮切线方向始终与加工轨迹相切。

其中条件（1）控制了运动单元与抛磨单元的相对位置，条件（2）和条件（3）决定了叶片和加工工具之间的姿态关系。

运动单元关节变量最终影响关节四工作台面圆心在基座标系下的位姿，如图9 所示，要想满足条件（1）和条件（2），基坐标系下关节四台面圆心(O4x,O4y)与(Bx,By)、(Px,Py)满足式（12）和式（13）的关系，其中X、Y是待抛磨点在叶片坐标系下的坐标。

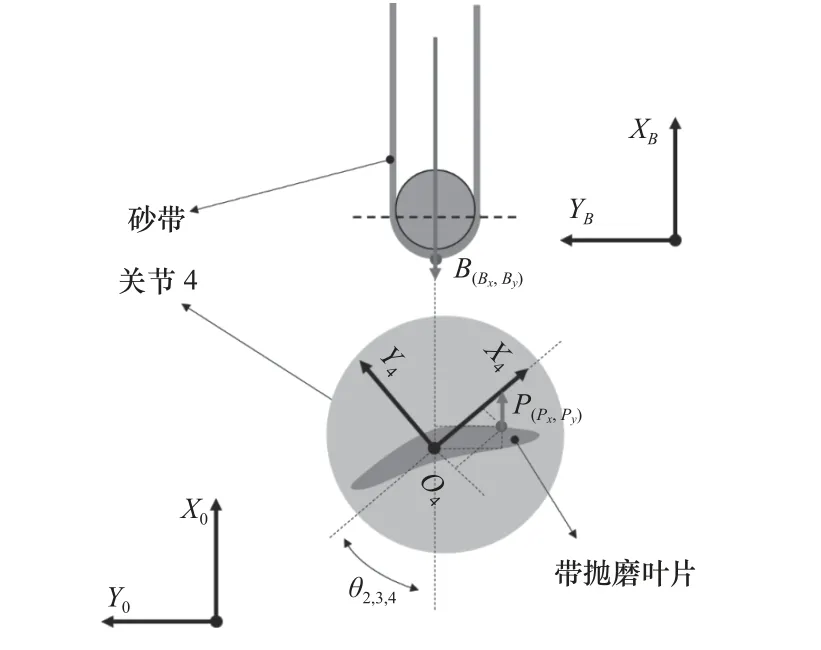
图9 协同运动局部俯视图

对于叶片型线法矢量在竖直方向的俯仰变换，如图10 所示，要想满足条件（1）和条件（2）可以得到以下关系：

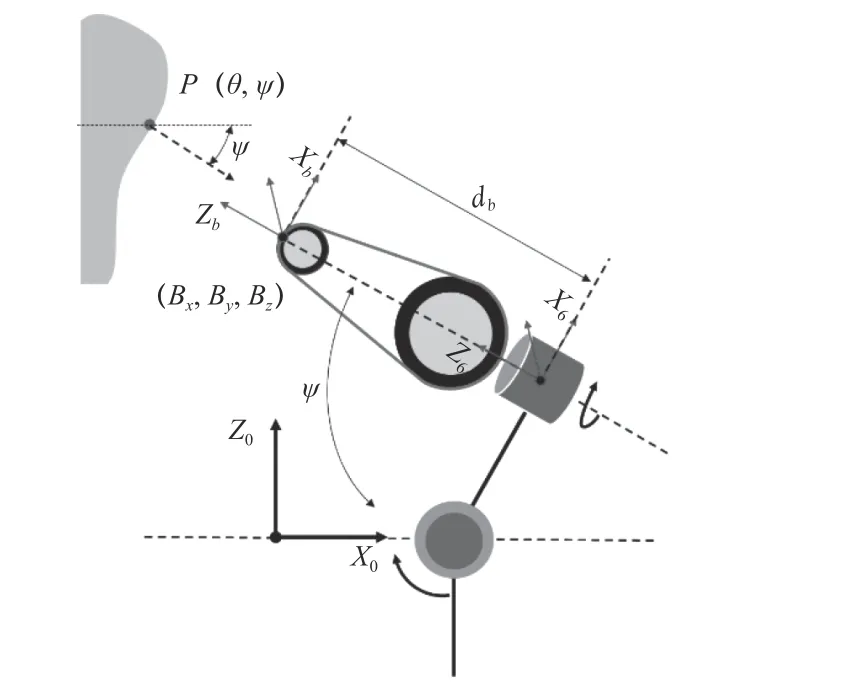
图10 协同运动局部侧视图

结合第三章运动学逆解结论，对于给定的叶片截面型线，当已知由刀位文件转换的NC 代码为（X,Y,Z,φA,ψB,θC）时，机器人各个关节运动的关节变量为

式（15）的解即为叶片抛磨机器人协同运动所必需的运动学逆解。

为了验证本章所求的机器人协同运动条件是否正确、关节运动过程是否存在干涉、离线编程软件算法是否准确、接触轮沿叶片截面型线运动过程中关节动力学情况，本文采用Adams 运动仿真软件模拟抛磨加工过程，采集关节运动数据并分析验证，验证流程如图11 所示。

图11 动力学仿真流程

仿真获得的机器人运动过程如图12 所示，观察仿真过程，两个单元运动协调，各关节在设计行程内运动，各关节连杆运动不干涉，砂带机接触轮最远端点紧贴叶片表面规划轨迹，验证了上文协同运动算法和离线编程软件的正确性。

图12 机器人运动过程

5 结语

本文基于自主设计研发的4+2 自由度叶片抛磨专用机器人系统，开展其抛磨轨迹规划方法研究。论文的主要研究结论如下：

（1）采用D-H 法分别建立机器人运动单元和叶片抛磨单元的运动学模型，推导2 个单元的运动学正逆解，再通过建立2 个单元协同运动模型实现叶片抛磨轨迹的执行，并通过运动仿真验证了该方法的可行性。

（2）在抛磨轨迹规划中，刀路轨迹的行距、刀路轨迹点的密度对抛磨误差有直接影响；复杂曲面柔性轨迹规划时，要考虑刀具和工件曲率半径干涉问题。