面向车次取消的票额分配与停站方案组合优化研究
孙立山,刘伊娜,许 琰,孔德文,邵 娟
(北京工业大学 城市建设学部,北京 100124)
0 引 言
高速铁路(高铁)给出行带来了极大地方便,并在一定程度上刺激了沿线城市的经济发展。但高铁的建设投资大、运营维护成本高、回报周期长,铁路公司面临着严重的债务问题。当列车受到严重干扰而被取消时,大量的旅客将会在车站滞留;若不及时疏散滞留旅客,不仅会激化旅客的不满情绪,还会造成客流流失,进一步加重铁路公司的经济损失。因此,当在列车被取消情况下,如何有序、高效地疏散滞留旅客,对保证列车服务质量、减少铁路公司损失具有重要的现实意义。
票额分配是以客流需求为基础,在一定席位容量限制下设置各路径票额数量的售票方法[1]。当列车运行发生突发情况时,合理的票额分配在一定程度上能达到及时疏散滞留旅客、减少铁路公司经济损失的目的。K.LITTLEWOOD[2]首次在航空领域利用收益管理理论对票额分配进行分析,建立了考虑分级票价的票额分配模型;A.CIANCIMINO等[3]首次将收益管理理论引入到铁路运输领域,建立了非嵌套式票额分配的确定性线性规划模型。基于此,学者们利用该概念对列车票额分配展开了大量研究。在城市轨道领域,由于旅客出行无固定坐席,学界大多是针对票价定价展开研究[4-6];但我国高铁采用的是固定坐席制且停站方案复杂,因此学者们在对高铁进行票额分配研究时的关注点也不尽相同。
作为票额分配的数据基础,客流需求对票额分配优劣有至关重要的影响。R.GOPALAKRISHNAN等[7]基于长距离旅客的需求,构建了票额分配的确定性线性规划模型,并对印度铁路票额分配方法进行了研究;包云等[8]将客流需求的预测模型嵌入到随机票额分配模型中,将得到的各OD确定性等客流作为输入,构建了以收益最大化为目标的单列车票额分配模型;P.HETRAKUL等[9]从旅客行为出发,在票额分配问题中引入乘客选择行为和需求的函数,提出了多项式对数模型和潜类模型形式的离散选择方法;WANG Xinchang等[10]基于客流需求服从非齐次泊松分布的假设,同步考虑旅客的选择行为,构建了单阶段和多阶段的票额分配模型,并将上述模型转化为等价确定性模型;强丽霞等[11]基于客流分配技术的票额分配优化基本原理,提出了客流分配流程,并进行了票额分配优化的研究;宋文波等[12]以收益最大化为目标,构建了单一列车的不确定客流需求动态定价与票额分配优化模型。
作为票额分配的关键约束,停站方案往往嵌入到票额分配的协同优化中。C.K.LEE等[13]将列车需求模型描述为具有广义成本函数的路径选择问题,并构建了上层考虑运营成本,下层考虑乘客出行的双层规划模型;HAN Bing等[14]以旅客满意度和平均入座率最大化为目标,搭建了高速铁路停站方案与票额分配的通用建模框架;赵翔等[15]基于多列车、多停站场景,构建了以收益最大化为目标的非线性整数票额分配模型;V.CACCHIANI等[16]在需求不确定情况下,通过限制列车旅行时间和停靠站数量,提出了求解停站方案和列车时刻表的整数线性规划模型。
目前关于票额分配的研究主要集中在列车运行计划制定阶段,其成果无法应用于列车取消等突发情况。当部分车次取消情况时,受后续列车停站方案限制,滞留旅客疏散需要增加停站,并同步调整后续列车的运行图;此外,滞留旅客中还存在着换乘其他线路的旅客,这就导致票额分配的情况更加复杂。因此,笔者基于列车容量限制的前提,分别考虑不优先疏散换乘旅客(no priority transfer passenger, NPT)和优先疏散换乘旅客(priority transfer passenger, PT)这两种情况,以停站方案与票额为决策变量,将后续列车剩余载客能力与列车停站约束进行关联,构建了票额分配和停站方案组合的优化模型,并通过算例验证了该模型的有效性。
1 问题描述
我国高速列车采用的是指定坐席制的票额分配方式。旅客在乘坐列车前,通常会提前购票并按照规定时间在规定座位就座。因此,当某些车次被取消时,对于被取消列车的旅客而言,只能选择在出发站和目的站均有停站计划且有剩余座位的后续列车。由于列车剩余容量有限,被取消列车的旅客可能无法全部成功改签到最早的后续列车上,导致部分旅客在车站等待时间较长或改选其他交通方式,这就进一步对铁路公司收益和旅客满意度造成损害。针对上述问题,笔者分别考虑NPT和PT两种情况,采取灵活停站策略,对被取消列车的旅客重新进行票额分配,以帮助旅客快速改签到后续列车,完成出行计划。
图1为列车计划运行图,G1~G5为在车站1~4之间运行的列车。列车停站计划是指在特定时间段内,明确列车在途经各个车站停留时间和顺序的计划。
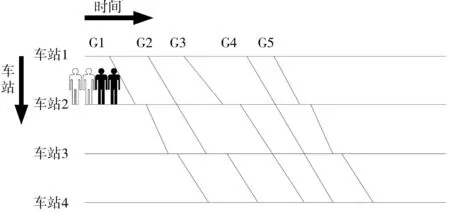
图1 列车计划运行图Fig. 1 Train schedule diagram
图1中:所有列车在起始站和终点站必须停车,G1在中间车站2、3有停站计划,G2在中间车站3有停站计划,G3在中间车站2有停站计划,G4在中间车站2、 3无停站计划,G5在在中间车站2、 3有停站计划。乘客只有在具有停站计划的车站才能进行乘降,其他车站无法组织旅客乘降。G2~G5是G1的后续列车且剩余载客能力均为1。白色和黑色旅客均准备乘坐G1从车站2出发,黑色旅客的目的地为车站3,白色旅客的目的地为车站4。
当G1因突发情况被取消时,为了到达目的地,滞留旅客会选择改签。对于黑色旅客而言,G5在车站2、 3有停站计划和剩余容量,可以作为改签的备选列车;对于白色旅客而言,G3、G5均在车站2、 4有停站计划和剩余容量,可以作为改签的备选列车。但由于后续列车容量和停站方案限制,滞留旅客可能改签失败,如图2。
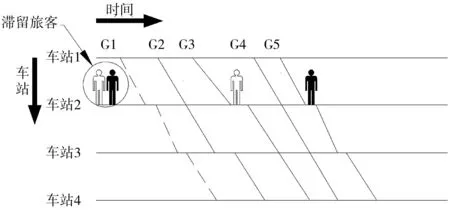
图2 滞留旅客搭乘后续列车方案Fig. 2 The plan for stranded passengers to board subsequent trains
为满足滞留旅客的出行需求,工作人员可在需求较大且后续列车有剩余容量的车站增加停站,如图3。G2、 G4在车站2增加停站后,G2成为黑色旅客的备选列车,G4成为白色旅客的备选列车。在停站方案调整后,通过重新分配票额来疏散滞留旅客,使得旅客顺利完成出行。

图3 增加停站后,滞留旅客搭乘后续列车Fig. 3 After adding stops, stranded passengers can board subsequent trains
此外,当滞留人数中存在少量有换乘其他线路需求的旅客(简称:换乘旅客)时,可将取消列车中所有旅客视为直达旅客进行疏散;当滞留人数中存在大量换乘旅客时,可优先考虑疏散换乘旅客,以免错过其他线路的接续列车,造成更大程度的延误。
2 模型构建
笔者构建了票额分配和停站方案组合优化的模型,主要分为模型假设、目标函数和约束条件等3个部分。
2.1 模型假设和符号定义
高铁的上下行方向列车分别占用不同的正线和到发线,相互独立不干扰,因此笔者针对双线铁路的单一方向票额分配和停站方案组合优化进行分析。为研究方便,笔者做如下假设:
假设1:滞留旅客不改变其需求,目的地为原计划车站;
假设2:滞留旅客仅在同一线路的单方向上进行改签,不考虑跨线改签;
假设3:列车在沿途各站均可停站。
模型所用符号及定义如表1、表2。

表1 模型参数Table 1 Model parameter

表2 模型变量Table 2 Model variable
2.2 目标函数
笔者从铁路公司收益和运营效率这两方面设置目标函数。
2.2.1 铁路运输公司收益最大化
铁路公司的收益与疏散旅客数量呈正相关。以铁路公司收益最大化为目标,在尽可能运送更多旅客的同时优先疏散远距离出行旅客。其目标函数Z1如式(1)。
(1)
2.2.2 偏离计划时刻表最小化
采用灵活停站策略会对原有的列车运行图带来影响。列车运行图调整过程中,为保证列车上原有旅客的出行计划,调整后的运行图应尽量减少与原有运行图的时间偏差,该目标函数Z2可通过式(2)来实现。
(2)
为将式(2)线性化,引入中间决策变量aki和dki。由于列车调整后实际离开的时间不能早于计划时间,故需要对列车实际到达时间与计划到达时间的差值进行线性化处理,如式(3)~式(5)。
(3)
(4)
(5)
2.2.3 归一化处理
为消除不同数据之间的量纲影响,需要将数据转换成无量纲的纯数值。笔者所考虑的两个目标函数单位分别为金额和时间,这两个函数值相差较大,若直接进行分析,会突出金额在分析中的作用;故需将目标函数进行归一化处理,使得各数据处于同一数量级后再进行分析。

(6)
若α越大,表明目标函数中铁路公司的收益权重越大,列车的偏离时间权重越小。
2.3 约束条件
为安全快速的疏散滞留旅客并保证所得解的可行性,笔者构建了列车停站方案、票额分配、列车时刻表等约束集。
2.3.1 停站方案与票额分配相关约束
式(7)为原有的停站约束。表示保留列车k原有的停站方案,保证对原有旅客的客运服务。
(7)
式(8)~式(9)为旅客需求约束。表示分配到列车k上OD对为(i,j)的票额数量不大于总需求。
(8)
(9)
式(10)为剩余容量约束。表示保证分配到每一列车上的旅客数量不能超过该列车的剩余容量。
∀k∈K,∀i∈S{Dk}
(10)
式(11)~式(12)为票额分配和停站方案一致性约束。表示当列车k没在车站i停靠时,分配到以车站i为起点(终点)的旅客数量为0,即当在车站i进行票额分配时,列车k必须在车站i停靠。
(11)
(12)
2.3.2 列车时刻表相关约束
式(13)~式(14)为到发时间约束。若因增加停站而需要对列车运行图进行调整,则调整后的列车在各个车站实际发车时间不能早于计划发车时间;同时考虑到列车上有换乘旅客,因此到达晚点时间不能超过换乘旅客的可接受范围。
(13)
(14)
式(15)为区间运行时间约束。表示列车区间运行时分不小于最小运行时分。
(15)
式(16)为最小停站时间约束。表示列车若在某一车站停车时,则停站时间不能小于完成必要技术操作所需要的最小时间;若列车在某一车站不停车,则停站时间为0。
(16)
式(17)~式(20)为列车安全间隔约束。表示为确保相邻两列车到达和离开同一车站时的必要安全间隔,保证列车安全运行。假定列车的站间旅行时间只与列车速度和车站之间的距离有关,且不允许列车在车站区间内进行越行。故相邻两列车离开车站i的顺序即为其在下一车站i+1的到达顺序。
∀i∈S{Dk,Dk′}
(17)
∀i∈S{Dk,Dk′}
(18)
k,k′∈K,∀i∈S{Dk,Dk′}
(19)
(20)
式(21)~式(23)为车站容量约束。由于列车到达或通过车站时必须占用车站线路且同一线路在同一时间只能被一列列车占用,而每个车站线路数量有限,因此需要设置列车容量约束,以保证列车经过该车站时至少有一条空闲线路供其使用。
(21)
∀k≠k′,k,k′∈K,∀i∈S{Ok,Ok′,Dk,Dk′}
(22)
(23)
3 算例分析
为验证文中模型的有效性,笔者以京沪线为背景进行算例分析。通过添加中间变量构建不等式组,将列车偏离计划时刻表最小化的非线性方程进行了线性化处理,优化模型均为线性方程。使用CPU为Intel(R) Core(TM) i7-7700HQ CPU@2.80 GHz,内存为16 GB的服务器,在Python3.7中调用GUROBI9.5.1商业求解器对模型进行求解。
3.1 算例描述
笔者以京沪高铁为背景,以南京南站到上海虹桥站下行区段为算例进行模型验证。图4为车站名称,右侧放大图中括号内的字母为车站代号;图5为NJN至SHHQ下行区段上的列车计划运行图。G0~G20代表各列车编号。
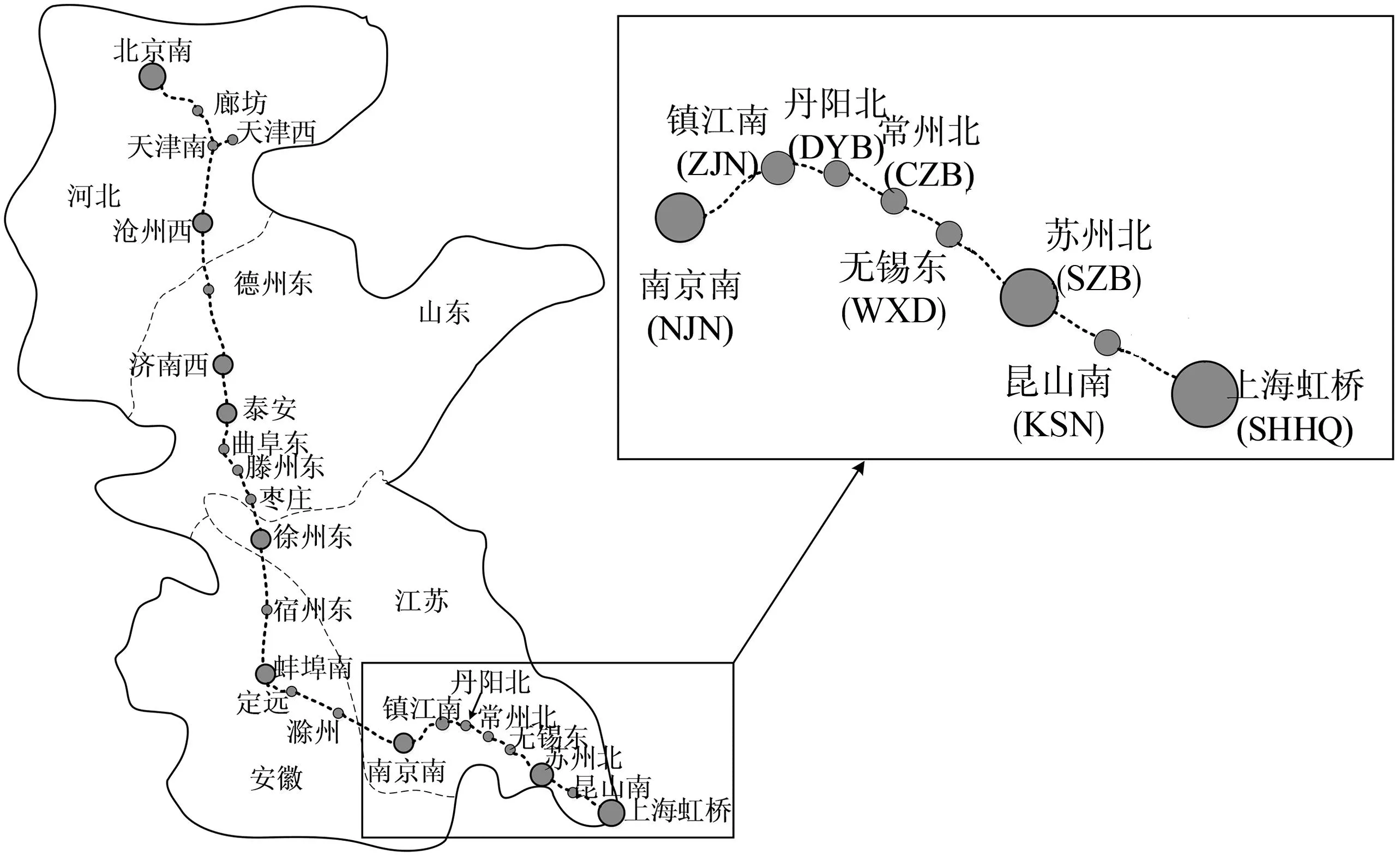
图4 京沪高铁车站示意Fig. 4 The Beijing-Shanghai high-speed railway

图5 列车计划运行图Fig. 5 Train schedule diagram
假设G0(虚线)受到严重扰动而被取消发车,后续列车均可正点发车。考虑到从NJN到SHHQ的乘客还可选择其他交通替代方式,例如客车大概需要4 h,故滞留旅客若等待后续列车时间过长,则会退票并选择其他交通方式出行,这对铁路运营收益造成较大损失。故笔者只选取运行时间在4 h之内的后续20列列车(实线,车次从左到右为G1~G20)。
3.2 数据准备
3.2.1 票价表
文中假设全部为二等座,参考NJN到SHHQ各区段真实票价,各OD直达票价如表3。
3.2.2 OD需求表
设置各列车每个区间最大载客量为810人,G0停站方案为NJN—ZJN—CZB—KSN—SHHQ,共服务10个OD区间,G0各OD区间的需求如表4。其中滞留旅客人数为各个OD对人数之和,共计1 060人。

表4 列车G0的OD区间需求Table 4 OD interval demand for train G0
3.2.3 其他数据
后续20辆列车各区间剩余容量总和与各个区段最小运行时间如表5。

表5 区间剩余容量总和与最小运行时间Table 5 Total remaining capacity of the interval and minimum operating time
假设始发站与终点站有足够多的股道数量,参考“京沪高速铁路动车组停车站到发线安排”,算例中各站股道数量设置如表6。此外相邻两列车到达和发车时间隔最小停站时间均为2 min,旅客可接受的到达晚点时间为5 min。
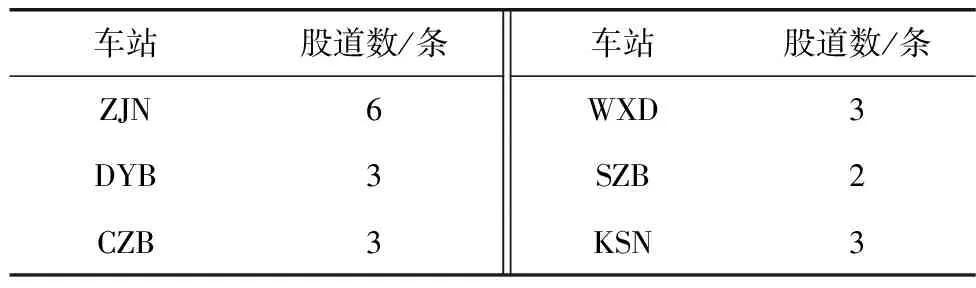
表6 各站股道数量Table 6 Number of lanes at each station
3.3 算例设计
3.3.1 参数n取值分析
为深入了解参数n对旅客疏散效果的影响,设定不同的α,并分析n取值从1~10对具有换乘需求滞留旅客疏散数量的影响,如图6。
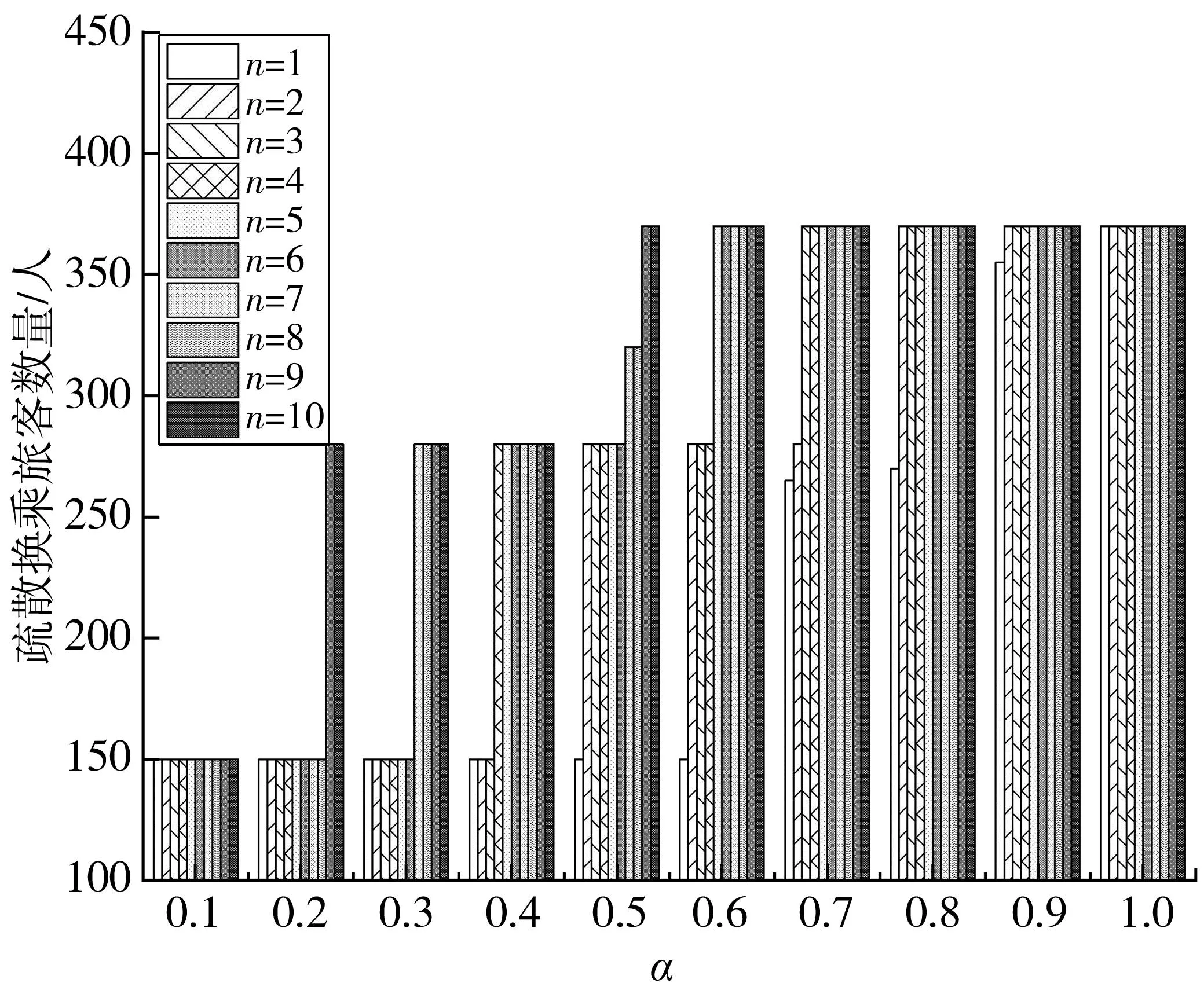
图6 不同α和n时,疏散换乘旅客数量Fig. 6 The number of evacuated passengers with transfer requirement for differen α and n
由图6可知:当α固定,随着n的增加,疏散具有换乘需求的旅客数量也显著增加。特别是当n取较大值时,即便α为一个相对较小的数,但仍可疏散较多具有换乘需求的旅客。具体而言,α=0.2时,当n从1增加至10,疏散具有换乘需求旅客数量增加了86.67%。
在实际中,调度人员可根据自己的偏好对n进行取值。笔者在优先考虑换乘旅客部分设置n=4来进行后续分析。
3.3.2 不优先考虑换乘旅客
在NPT情况下,可通过灵活停站策略对滞留旅客进行疏散。图7表示不同α下的疏散旅客数量与实际收益关系;图8表示不同α下的列车偏离时间与增加停站数量关系。由图7、图8可知:随着α增大,疏散的滞留旅客数量增多,铁路公司收益增加,列车增加停站数量增多,列车偏离时刻表时间也随之增长。这说明为疏散滞留旅客而增加停站,对列车偏离原时刻表时间有一定影响。除此之外,在一定范围内改变目标函数权重系数并不会改变最优解,且随着滞留旅客数量减少,α增大对铁路公司收益的影响程度也随之减少。

图7 NPT时,不同α的疏散旅客数量与实际收益Fig. 7 Number of evacuated passengers and the actual revenue for different α in the NPT case
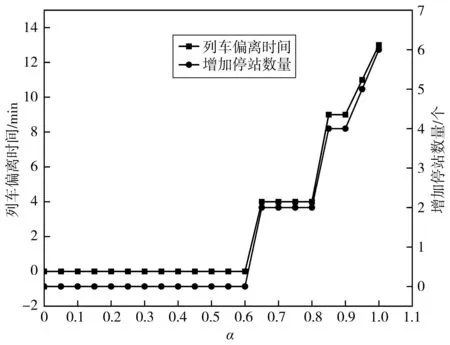
图8 NPT时,不同α的列车偏离时间与增加停站数量Fig. 8 Train deviation time and the number of adding stops for different α in the NPT case
算例中,当α从0.6增加到0.65时,铁路公司的收益增量最大。图9为α=0.65时,调整后的列车运行图。
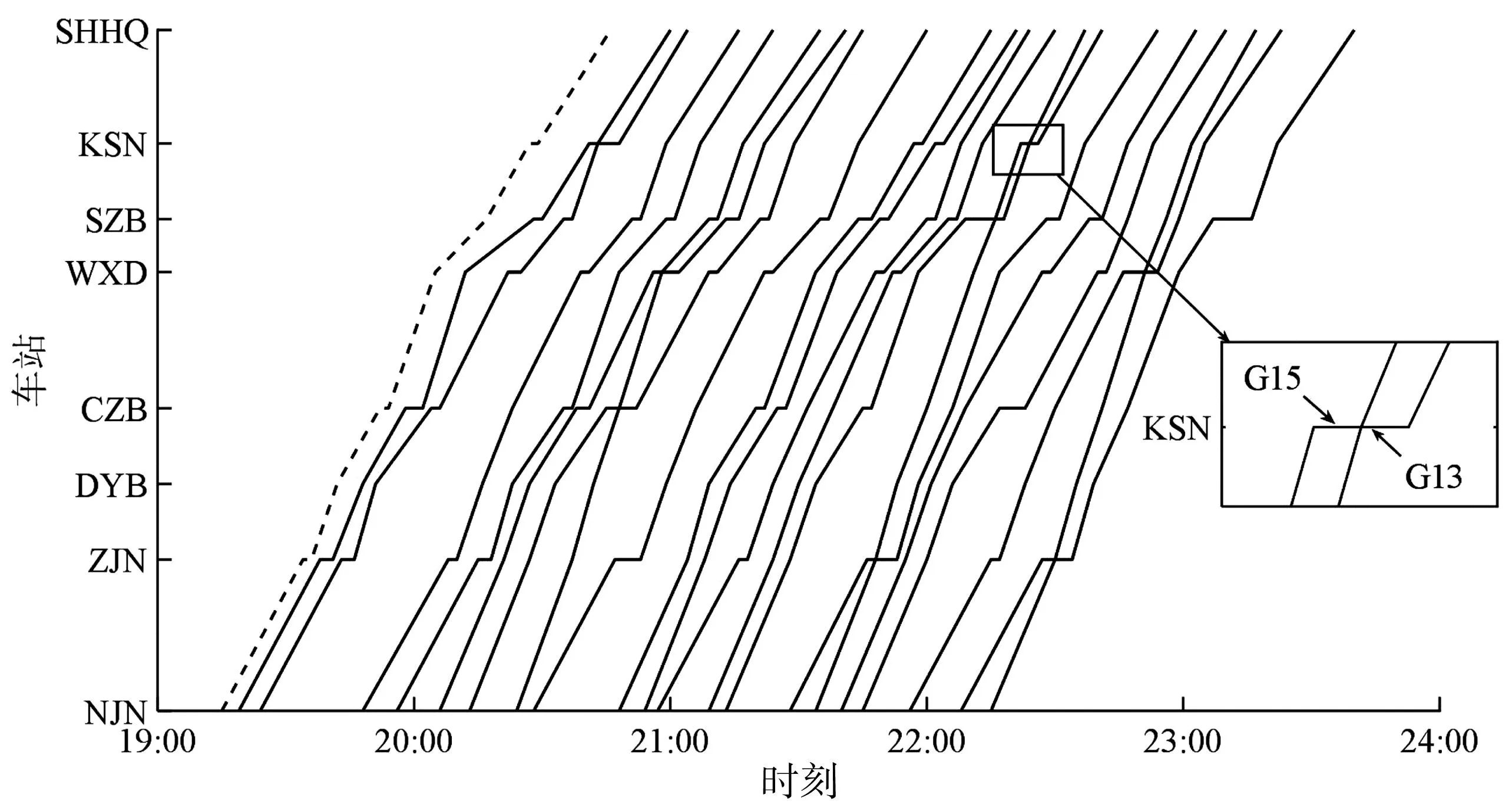
图9 调整后的列车运行图(α=0.65)Fig. 9 Train operation chart after adjustment (α=0.65)
图9中:G13、G15在昆山南站增加停站,后续列车偏离时刻表4 min,疏散人数增加26.8%,铁路公司收益增加27.0%,相应的票额分配方案如表7。

表7 票额分配结果(α=0.65)Table 7 Ticket allocation results (α=0.65)
3.3.3 优先考虑疏散换乘旅客
当取消列车中换乘旅客的数量较多时,可优先考虑疏散换乘旅客。图10为不同α下的疏散旅客数量与实际收益(PT情况下);图11为不同α下的列车偏离时间与增加停站数量(PT情况下)。由图10、图11可知:在PT情况下,随着α增大,疏散滞留旅客数量与列车偏离时刻表时间的变化趋势与NPT基本相同。算例中,当α从0.3增加到0.35时,铁路公司的收益增量最大。
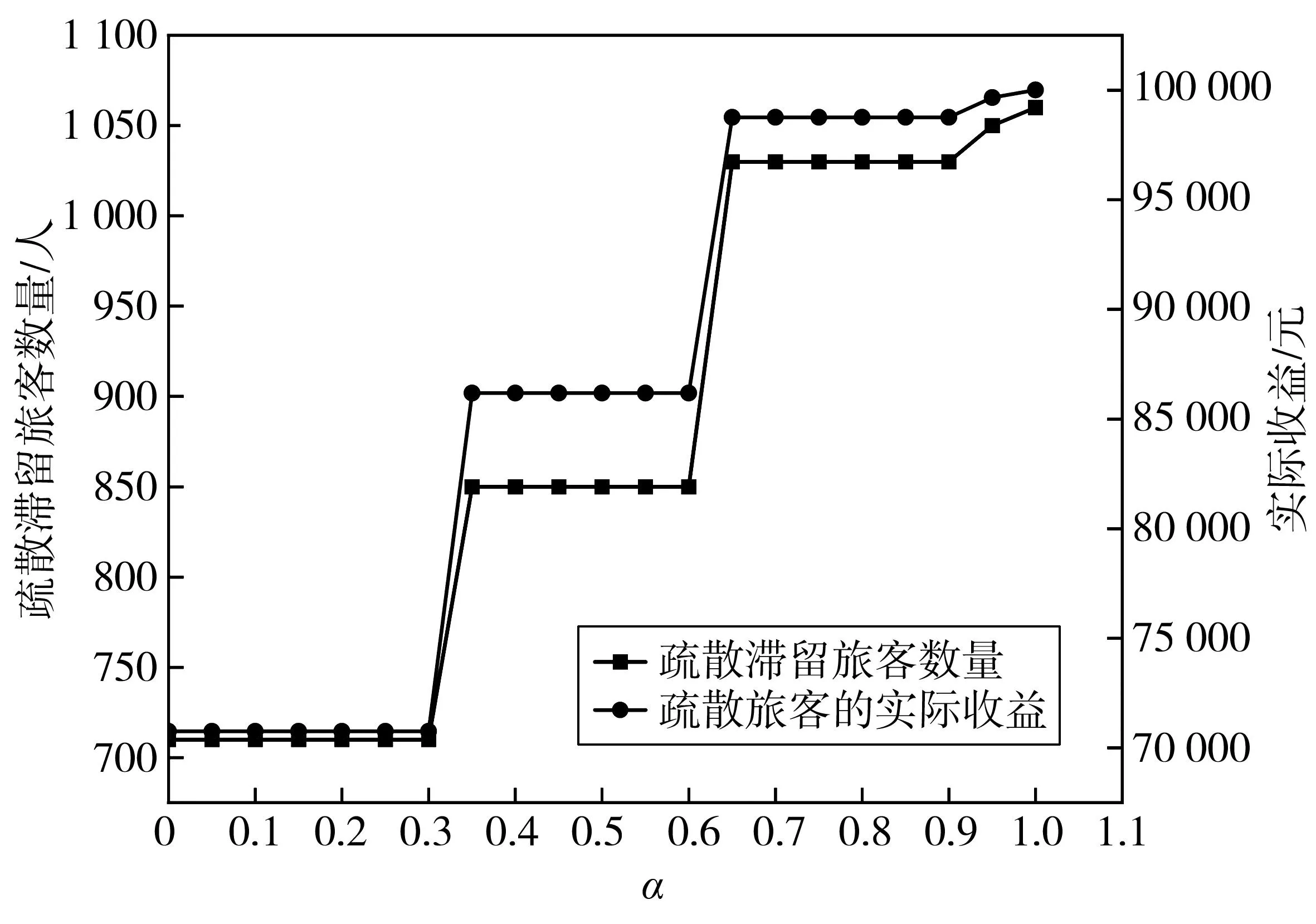
图10 PT时,不同α的疏散旅客数量与实际收益Fig. 10 Number of evacuated passengers and the actual revenue for different α in the PT case

图11 PT时,不同α的列车偏离时间与增加停站数量Fig. 11 Train deviation time and the number of adding stops for different α in the PT case
图12为α=0.35时,调整后列车运行图。图12中:G18、G20在昆山南站增加停站,后续列车偏离时刻表4 min,疏散人数增加19.7%,铁路公司收益增加21.8%,相应的票额分配方案如表8。

表8 票额分配结果(α=0.35)Table 8 Ticket allocation results (α=0.35)
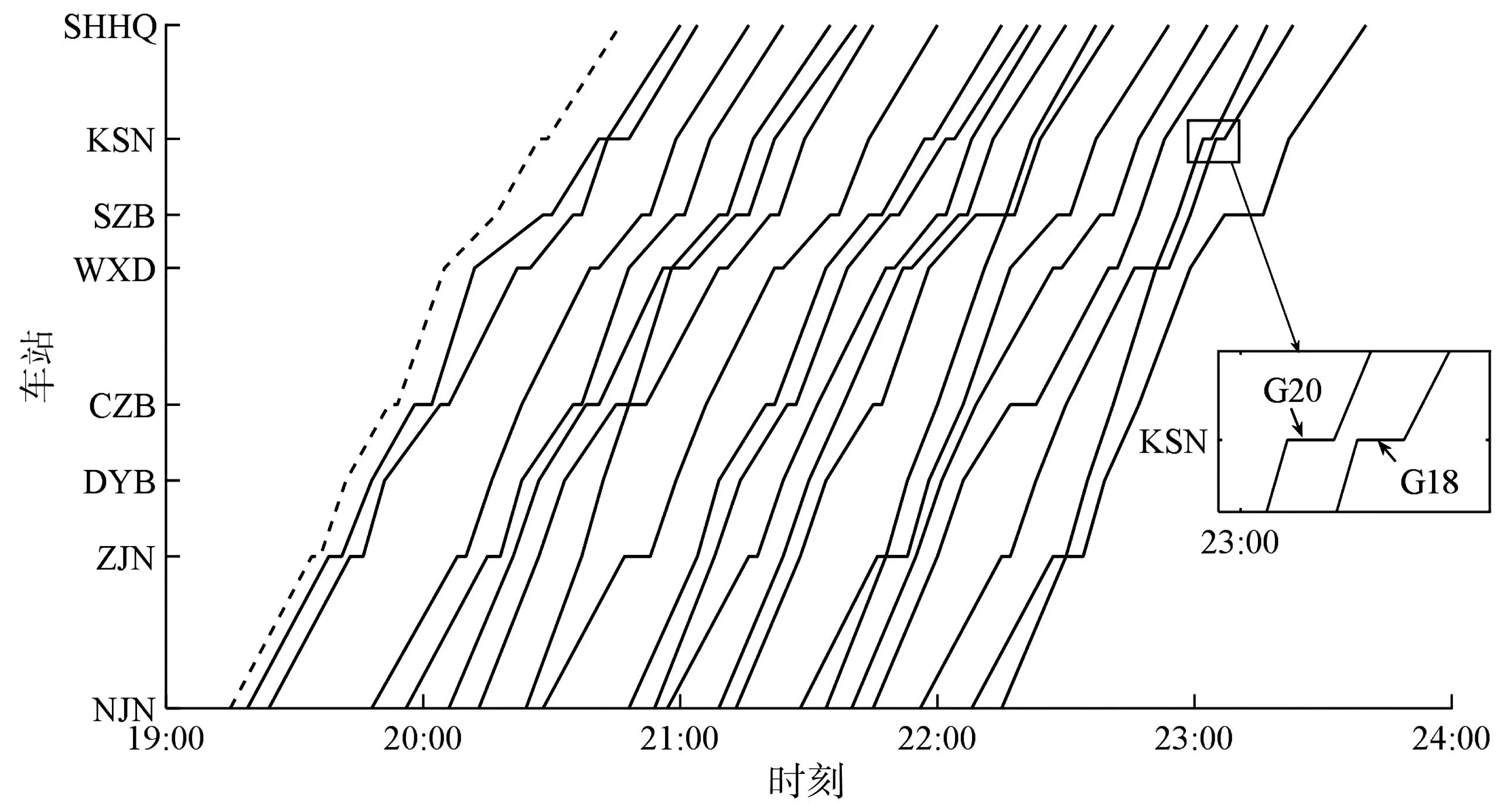
图12 调整后的列车运行图(α=0.35)Fig. 12 Train operation chart after adjustment (α=0.35)
综上可知:在不优先疏散换乘旅客和优先疏散换乘旅客这两种情况下,采用灵活停站策略可有效地疏散滞留旅客。此外,α取值应结合实际情况选用。若滞留旅客较多,则可通过增大α获得一个疏散滞留旅客较多的解;若滞留旅客较少,则列车准时性更加关键,应选择使列车总体偏离时间较小的解。
4 结 论
1)笔者针对当列车取消时,利用票额分配来疏散滞留旅客的问题进行了研究。研究表明:针对不优先疏散换乘旅客和优先疏散换乘旅客这两种情况,采用灵活的停站策略可有效疏散滞留旅客。
2)采用灵活停站策略时,应根据滞留旅客数量灵活选用α值。若滞留旅客较多,则应通过增大α获得一个疏散滞留旅客较多的解;若滞留旅客较少,则列车准时性更加关键,应选择使列车总体偏离时间较小的解。α从0.6增加到0.65时(PT情况下),铁路公司收益增量最大,疏散人数增加26.8%,收益增加27.0%;当α从0.3增加到0.35时(NPT情况下),铁路公司收益增量最大,疏散人数增加19.7%,收益增加21.8%。
4)随着问题规模的扩大,如何根据问题特点设计更加高效的算法(比如滚动时域算法)是笔者下一步研究的重点。

