基于AOA-LSSVM模型的枢纽城市物流需求量预测

肖 红,夏如玉,王孝坤,杨雪峰

(1. 重庆交通大学 经济与管理学院,重庆 400074; 2. 重庆口岸物流与航运发展研究中心,重庆 400074; 3. 大连交通大学 经济管理学院,辽宁 大连 116000; 4. 大连交通大学“一带一路”交通互联互通与人文交流研究院, 辽宁 大连 116003; 5. 辽宁省交通运输事业发展中心,辽宁 沈阳 110005)

0 引 言

区域物流需求预测是制订物流发展规划、项目决策并提升物流综合效益的重要依据。用于物流需求预测的理论方法可分为定性和定量两大类[1-2]。定性预测方法主要包括德尔菲法、专家调查法、主观概率法等。定性预测法较灵活,预测简单迅速,但易受主观因素的影响,难以对物流需求作数量上的精确描述[3]。定量预测方法则是利用历史数据或因素变量来预测未来物流需求的数学模型[4]。

物流需求定量预测方法主要有时间序列法、因果关系法、组合预测法、人工智能法等。时间序列预测法通过简单的模型,便能对物流需求预测做出比较好的解释[5];因果关系法是利用事物发展的因果关系来推断事物发展趋势的预测方法[6];组合预测方法的基本思想是将两个及以上的单一模型预测结果通过赋权形式组合,从而减弱原预测模型的预测误差,得到更精确的预测结果[7]。时间序列预测法通常以假设条件为前提建立模型,很难全面揭示数据内在的复杂特性。组合预测法可以有效提高预测精度,但是采用组合预测的模型受权重系数选取的影响较大,使预测的工作量增加。

随着信息和计算机科学的发展,智能预测方法被广泛应用于物流需求中。神经网络作为一种人工智能方法,能够较好刻画物流需求与其影响因素间的非线性映射关系。蔡婉贞等[8]为解决物流需求的非线性问题,提出了一种BP与RBF相结合的组合预测模型,结果表明神经网预测模型效果更好。但神经网络所需数据量较大,实际问题中经常遇到过学习、陷入局部极值等问题。最小二乘支持向量机(LSSVM)对物流需求预测有着独特的优势,它不仅解决了物流需求中的非线性问题,还降低了算法的复杂性,提高预测精度。J.A.K.SUYKENS等[9]提出LSSVM是将支持向量机(SVM)的非线性二次规划方程组转化为线性方程组,降低了计算复杂性,为复杂的物流需求预测提供一种新方法;耿立艳等[10]通过LSSVM智能预测模型对物流需求进行了预测,预测结果都优于其他(WNN、SVM)组合预测模型。为进一步提高预测精度,F.A.HASHIM等[11]提出阿基米德优化算法(AOA),通过此算法解决数值优化问题,并提高模型的收敛速度,可有效解决复杂问题;郑婷婷等[12]将AOA与鲸鱼优化算法、灰狼优化算法等进行了比较,发现AOA算法对大规模优化问题具有更高的稳定性和寻优能力。

以LSSVM为代表的人工智能方法,具有较高的非线性拟合精度,可用来更好解决复杂的物流需求预测问题,以获得更高的预测精度并降低计算难度,也使得LSSVM在物流需求预测中具有较好的适用性。由于西部陆海新通道枢纽城市运输系统受到运输结构调整的影响,不确定性因素影响突出。为进一步简化、提高物流需求预测精度,提出一种AOA和LSSVM结构相结合的预测方法,将AOA算法应用到LSSVM模型中。先采用灰色关联分析(GRA)选择物流需求主要影响因素,将其作为输入变量,建立LSSVM预测模型,再利用AOA优化LSSVM参数,最后通过对西部陆海新通道的重要枢纽城市——重庆、成都、贵阳和南宁物流需求的实例研究检验新方法的有效性。

1 模型构建

1.1 LSSVM模型构建

SVM是根据结构风险最小化(structural risk minimization,SRM)准则与统计学习理论提出的[13]。 LSSVM是将SVM中的非等式方程组转化为等式方程组,并通过最小二乘线性系统作为代价函数,用于LSSVM模型的参数估计,使得误差的平方项最小化,从而提高计算精度。LSSVM具体方法如下:

给定一个训练样本集合为L={(xi,yi),i=1,2,…,N},其中,xi∈R输入变量,yi∈R为对应的输出变量,N为样本个数,对于y(x)=ωTφ(x)+b非线性回归函数,LSSVM基于SRM准则,将构建其目标函数如下:

(1)

式中:ω为权重向量;b为偏置常量;γ为正则化参数;ei为第i个误差变量;φ(·)为非线性映射函数。

通过引入拉格朗日乘子向量αi和KKT条件,则将拉格朗日函数定义为:

(2)

式中:αi为拉格朗日乘子向量;ei为误差变量。

分别对L(ω,b,e,α)中的ω,b,e和α求偏微分:

(3)

消去式(3)中的ω、ei,可最终简化为:

(4)

式中:K(x,xi)为核函数。

1.2 AOA算法

AOA算法的原理是物体通过相互碰撞,不断调整自身密度和体积,使物体达到平衡状态。其中调整的过程即为种群寻优过程,达到平衡状态的个体则是全局最优解。此算法不仅可以避免陷入局部最优值,提高收敛速度。还可以对LSSVM模型的参数进行寻优迭代,以找到一个最小误差值,使LSSVM模型整体的预测性能提高,以提高整个模型的预测精度,从而找到模型的正则化参数(γ)和核函数(σ)最优值,具体算法如下:

1)初始化

对所有对象的位置进行初始化处理,如式(5);对每个第i个对象的体积(vi)、密度(di)以及加速度(ai)进行定义,令vi与di为[0,1]范围的随机数,其余如式(6):

Oi=li+R′×(ui-li),i=1,2,…,N

(5)

ai=li+R′×(ui-li),i=1,2,…,N

(6)

式中:Oi是N个对象中的第i个物体的位置;ui和li为搜索空间的上下边界;R′为[0,1]范围的随机数。

2)更新

为更好的评估初始总体,并选择出最佳适应度的对象vbest、dbest、abest。因此,更新密度及体积公式,得到公式(7):

(7)

式中:dbest和vbest是到目前为止发现的对象的最优密度和体积;abest是对象的最优加速度。

3)计算转移算子(T)与密度因子(d)

对象之间发生碰撞时,通过T和d的计算,使对象试图达到平衡状态,增强AOA算法的局部搜索能力,如式(8):

(8)

式中:t为迭代次数;tmax为最大迭代次数。

4)开发阶段

若对象之间发生碰撞,当T≤0.5,随机选择一个对象,使用式(9)计算t+1次迭代对象的加速度,当T>0.5时则进行勘探开发行为。

(9)

式中:dmr、vmr和amr是随机对象的密度、体积和加速度。

若对象之间无碰撞,当T≤0.5时进行勘探开发行为,当T>0.5时,使用式(10)计算t+1次迭代对象的加速度:

(10)

将式(9)和式(10)进行标准化,如式(11)。

(11)

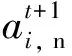
5)对象位置更新

若T≤0.5,第i个t+1迭代时,使用式(12)对对象位置更新:

(12)

若T>0.5,使用式(13)对第i个t+1迭代时对象位置更新:

(13)

式中:Orand是种群中对象的随机位置;Obest为对象的最佳位置;C1、C2为常数,通常取2和6;D定义为常数C3乘以转移算子(T);F是决定对象位置更新的标志,将其定义为:

(14)

式中:P=2×R′-C4,其中C4为常数。

2 实证分析

根据国家发展改革委2019年颁布的《西部陆海新通道总体规划》,重庆、成都、贵阳和南宁为通道的重要枢纽城市,笔者以此4座城市为研究对象,对其物流量进行预测研究。4座枢纽城市物流需求预测的影响因素为经济发展水平、产业结构、国内外贸易、收入及消费水平、固定资产投资等。

2.1 物流需求影响因素的选取

在物流需求的度量指标中,现有研究主要采用货运量(Y1)和社会物流总费用(Y2)两种:①货运量(Y1)指标,是利用不同的预测方法将货物量作为物流需求的预测值,但在西部陆海新通道整个物流系统中,货运量仅仅代表运输通道的货物流向,并不能完全反映枢纽城市的物流需求量[14-15];②社会物流总费用(Y2)指标,该指标不仅从核算角度定义了物流需求,还能代表物流活动中各项费用支出[16]。将采用Y2作为西部陆海新通道的物流需求量化指标,物流需求影响因素如表1。

表1 物流需求影响因素Table 1 Influence factors of logistics demand

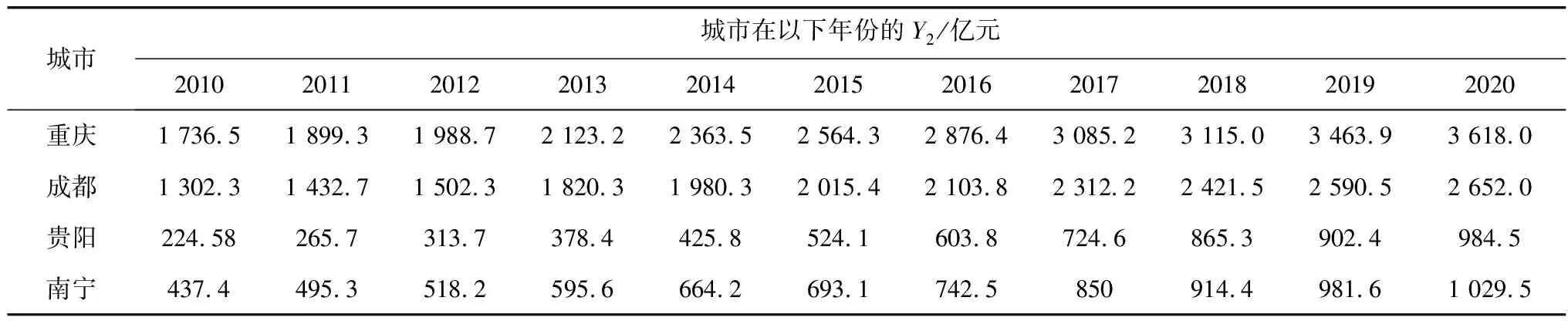
表2 重庆、成都、贵阳、南宁的社会物流总费用(2010—2020年)Table 2 Total costs of social logistics in Chongqing, Chengdu, Guiyang and Nanning (2010—2020)

计算中,2010—2020年物流需求量(Y2)以及影响因素指标代码(x1～x11)的数据分别来源于:

1)表1中2010—2012年重庆、成都、贵阳、南宁的社会物流总费用(Y2)数据由于相关政府部门未公开,数据来源参考文献[16],通过社会物流总费用(Y2)除以GDP值的比例逆向推导出社会物流总费用(Y2)的值,具体如表(2);2013—2020年重庆、成都、贵阳、南宁的社会物流总费用(Y2)数据来源于重庆市统计局、重庆市发展和改革委员会、重庆市口岸与物流办公室、成都市统计局、成都市发展和改革委员会、成都市口岸与物流办公室、贵阳市统计局、贵阳市发展和改革委员会、贵阳市口岸与物流办公室、南宁市统计局、南宁市发展和改革委员会、南宁市口岸与物流办公室相关资料;

2)影响因素(x1～x11)数据来源于《重庆市统计年鉴2021》、《成都市统计年鉴2021》、《贵阳市统计年鉴2021》、《南宁市统计年鉴2021》。

2.2 灰色关联分析(GRA)

根据式(15)进行灰色关联度分析,分析如式(15),分析结果如表3。

(15)

参考文献[17],设定γ0i的取值范围。当γ0i>0.60,该因素对枢纽城市物流需求的关联度越大;反之,当γ0i≤0.60,该因素对枢纽城市物流需求的关联度越小。由表2可知,西部陆海新通道中重要枢纽城市——重庆、成都、贵阳、南宁的γ0i在0.603～0.870间,说明所有因素都具有一定关联性,但为了提高预测准确度,降低计算难度,将γ0i值最低的4项:第三产业总产值(x4)、居民可支配收入(x6)、居民消费水平(x7)与地区消费品零售总额(x8)剔除;剩余7项:地区GDP(x1)、第一产业总产值(x2)、第二产业总产值(x3)、人口规模(x5)、进出口贸易总额(x9)、固定资产投资(x10)、运输总里程(铁路、公路、水路)(x11)影响因素作为西部陆海新通道中重要枢纽城市的物流需求预测的主要因素。

2.3 数据处理与模型训练

通过2.2节的灰色关联度分析,根据式(16)将枢纽城市的全部样本数据进行归一化处理,再将归一化后的数据分为训练集和测试集。

(16)

式中:S和St分别是原始数据和归一化后的数据;Smax和Smin分别为原始数据的最大值和最小值。

将2010—2017年数据作为AOA-LSSVM模型的训练集,2018—2020年的数据作AOA-LSSVM模型的测试集,用于验证AOA-LSSVM模型的预测性能。AOA算法的自身控制参数设置如表4。

表4 参数设置Table 4 Parameter setting

表4中系数b1、b2选取依据是式(1)中的偏置常量b。ϑ的选取依据根据文献[19],其原理是物体通过不断调整自身密度和体积,物体达到平衡状态,这个平衡状态有一定的取值范围,ϑmax、ϑmin代表的就是物体平衡状态的最大值和最小值。

在AOA中对参数组合(γ,σ)计算过程中,会产生一定范围内的误差。误差越大,所对应的LSSVM模型中的参数组合(γ,σ)越不理想,导致AOA-LSSVM模型预测效果不佳。笔者通过增加AOA算法优化LSSVM的参数次数,选择相对误差最小对应的参数组合(γ,σ),基于此组合建立LSSVM模型并预测2018—2020年西部陆海新通道枢纽城市的物流需求,根据式(16)将预测值进行逆归一化处理,获得原始物流需求的预测值。

经过AOA算法对粒子进行搜索迭代,使得每个粒子获得最优位置(Obest),最优密度(dbest),最优加速度(abest)。通过位置的更新,AOA-LSSVM模型也获得了最优的参数组合(γ,σ),基于(γ,σ)对AOA-LSSVM模型进行迭代,迭代适应度变化如图1。由图1可知,AOA算法在迭代20次,已到达最佳适应度值。说明此算法具有良好的收敛稳定性、寻优搜索能力能强的特点。

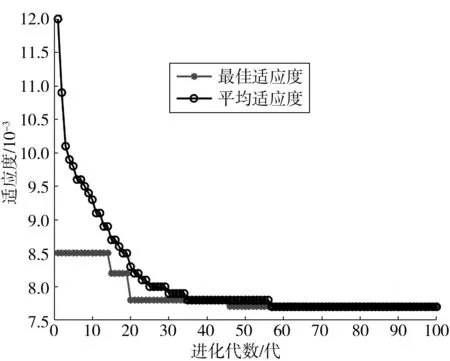
图1 适应度曲线Fig. 1 Fitness curve

2.4 AOA-LSSVM模型和LSSVM模型的比较

为了进一步验证阿基米德算法在LSSVM模型的预测效果,将AOA-LSSVM预测结果与LSSVM预测结果相比较。选用均方根误差(RMSE)、平均绝对误差(MAE),以及异方差调整的均方根误差(HRMSE)、异方差调整的平均绝对误差(HMAE)4项指标对这两种模型进行评估性能。如果这些指标数值越小,表明模型的预测性能越好。

表5、表6分别列出了LSSVM和AOA-LSSVM两种模型的误差指标对比及两种模型的预测结果,可见:

表5 LSSVM与AOA-LSSVM两种模型的误差指标对比Table 5 Comparison of error indicators between the two models of LSSVM and AOA-LSSVM

表6 LSSVM和AOA-LSSVM两种模型预测结果及误差情况Table 6 The prediction results and errors of the two models of LSSVM and AOA-LSSVM

1)由2018—2020年西部陆海新通道4大枢纽城市的物流需求预测可知,各个枢纽城市的AOA-LSSVM模型的相对误差值均小于LSSVM模型,,说明AOA-LSSVM模型提高了预测精度。

2)AOA-LSSVM模型的预测性能也优于LSSVM模型,其RMSE、MAE、HRMSE、HMAE值均小于LSSVM模型的对应值,分别降低了1946.4,1206.1,0.028 4,0.039 7。这主要是由于AOA算法使物体达到平衡的最佳状态,增强了算法的全局搜索能力,进而正确找到了LSSVM的最优参数,提高了LSSVM的预测性能。

2.5 AOA-LSSVM模型预测结果

利用AOA-LSSVM模型预测西部陆海新通道中重要枢纽城市的物流需求量,结果见表7。由表7可知,西部陆海新通道的枢纽城市的物流需求在2025、2030、2035年的社会物流总费用预计将达到10 273.8、12 340.4、14 077.1亿元,其预测结果为西部陆海新通道物流枢纽城市的物流建设和运营提供了的理论依据。

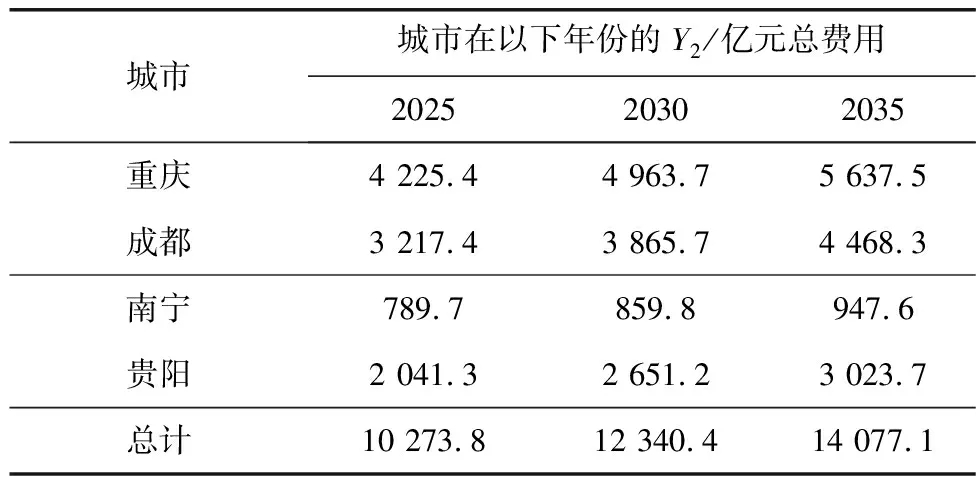
表7 西部陆海新通道的枢纽城市的物流需求预测值Table 7 Predicted value of logistics demand in hub cities of the new western land-sea passage

3 结 论

为了提高LSSVM模型整体的预测精度,通过对传统的LSSVM模型进行改进,构建阿基米德算法(AOA)优化最小二乘支持向量机(LSSVM)智能预测模型,具体结论如下:

1)通过阿基米德算法对传统的LSSVM模型进行改进,使得模型得到最优的(γ,σ)值,避免了传统的LSSVM难以全面反映物流需求的变化规律,从而导致预测效果不佳的问题。并利用AOA-LSSVM模型对西部陆海新通道中重要枢纽城市—重庆、成都、贵阳和南宁在2025、2030、2035年的物流需求量进行预测,并得到了相关的预测值。

2)选用的AOA算法由于具有强大的全局搜索能力,在改善LSSVM预测性能和建模速度方面的效果尤为显著,因此,基于AOA算法优化的LSSVM模型是一种更为有效的物流需求预测方法,具有一定推广应用价值。