精选素材,深度教学:复习备考课堂教学的“三度”

⦿ 山东省济南市莱芜第一中学 王晓飞

随着《普通高中数学课程标准(2017年版)》的颁布与实施,在复习备考数学课堂上更加突出实现教师的教育价值,实现以学生为主体的“人”的教育,是高考复习备考过程中不得不引起思考且高度重视的一个课题.

而对于学生的学习,有三个关键要素,即学科本身、数学内容、教师角色.深度教学就是有机“串联”起这三个关键要素的纽带,必须从学科本身的深化、数学内容的理解以及教师角度的转化等层面来合理优化,从而使得教学知识与内容真正达到“教活、教透、教深”,实现课堂教学的深度化尝试与应用.

1 素材的恰当选择,让教学有“效度”

高中数学教材是“课标”的载体,例(习)题以及一些相关的栏目是教材的重要内容之一,也是基础知识的经典载体.这些教材的典型素材,成为历年高考数学命题的重要场景与依据,同时也给教材的正确使用提供了更加广泛的空间与应用场景.

近年高考数学真题与最新的高考模拟题,是高三复习备考课堂教学的典型素材,也是教育专家与一线教师对课标与教材的各方面视角的解读与展示,对于课堂教学有很好的“效度”.

(1)它到直线l的距离最小?最小距离是多少?

(2)它到直线l的距离最大?最大距离是多少?

A.13 B.12 C.9 D.6

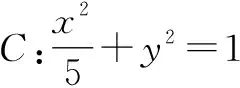
教师通过课堂的合理创设与剖析,引导学生从特殊到一般、从一般到特殊等视角的探究,从而得以分析与解决问题,得到相关的性质与结论.探究性学习与教学实际,必须在教师合理引导下,充分发挥学生的主体,并通过双方的协同,结合合理的变式与拓展来开拓知识的“效度”.

因此,在高考数学复习备考时,一定要回归教材,让教材的经典例(习)题、关于创造的栏目以及历年的高考真题等,在原来练习的基础上,加以合理变式、推广、拓展等,更好地发挥其教学作用.

2 学生的创造表现,让教学有“宽度”

在高考复习备考课堂教学中,教师要充分备课,精选素材,合理设置环环相扣的问题,符合学生的认知规律.在实际教学过程中,学生的主体参与以及深入学习,这才是教学的根本所在,也是充分体现教师备课效果、学生学习结果的重要过程.

只有充分体现学生的主体性,以及在此过程中不断提升数学解题能力,才能不断增强学生的积极性与主动性,也对深度教与学起到促进与增强的作用.

例2(2023届江苏省苏锡常镇四市高三教学情况调研数学试卷·8)已知数列{an}的前n项和为Sn,a1=1,若对任意正整数n,Sn+1=-3an+1+an+3,Sn+an>(-1)na,则实数a的取值范围是( ).

层次一:解题思维的创造.

通过教师的合理引导,从破解问题的不同思维视角来分析与解决.

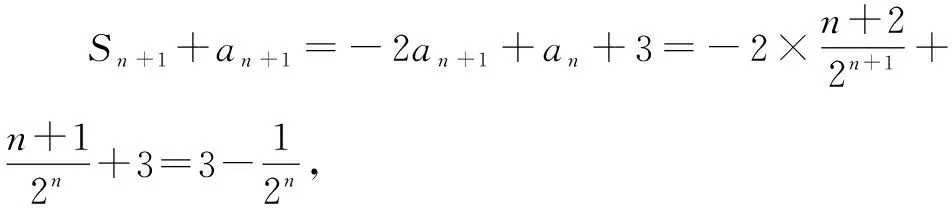
层次二:发展思维的创造.

在教学与学习过程中,借助学生的热情参与,不断提升实践和探索机会,让学生真正全身心地投入到问题的学习、解决、应用等过程中,数学知识、数学思想与数学能力等方面的发展与应用才能落到实处.

3 知识的灵活应用,让教学有“深度”

在教学过程中,对于一些典型知识与教材内容,总结规律,把握技巧,让学生回归基础、回归教材,树立夯实基础的意识,使教学与学习更加有“深度”.

例3〔2023届湖北省七市州高考数学调研试卷(3月份)〕已知M(1,2)为抛物线C:y2=2px(p>0)上一点,过点T(0,1)的直线与抛物线C交于A,B两点,且直线MA与MB的倾斜角互补,则|TA||TB|=______.

通过讲解与分析,归纳以下相应的结论,并在此基础上合理深入应用与变式拓展.

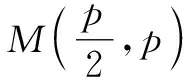
变式1已知M(1,2)为抛物线C:y2=2px(p>0)上一点,过点T(0,1)的直线与抛物线C交于A,B两点,且直线MA与MB的倾斜角互补,则直线AB的方程为______.(y=-x+1.)

在此基础上,借助深入学习与变式拓展,合理体验解题过程与解题的一般化,迁移解题思路和思想方法,灵活应用数学相关知识,从而进一步迁移到不同的数学问题情境与数学应用中,让学生体验数学思想方法的应用,提高数学解题能力,让数学教学与数学学习更加有“深度”.