严谨性思维的培养措施

⦿ 江苏省江都中学 王 斌

思维的严谨性属于思维品质的一种,主要指对待问题时要遵循逻辑规则,在概念清晰的状态下进行准确判断、有据推理,体现思维的缜密性.在教学中,教师常发现学生遇到一些跨度大的证明题就不知从何下手;有些需要分类讨论的问题,常常出现遗漏的现象.这些问题的发生,都是因为思维不够严谨而导致的.因此,在教学实践中,笔者特别对培养学生思维的严谨性作了一定的研究,与同行共勉.

1 问题诱导,准确表述

想要在数学学习中获得严谨的思维,必须准确无误地表述并理解数学概念、定理、公式、定义、法则等基础知识.尤其是概念中呈现的一些关键性词语,必须保证能用数学符号进行精确化的表达.为了达到这一目的,教师可设计一些具有引导性的问题,以激发学生探究的热情,让学生对抽象的知识产生良好的情感倾向.

问题的设置需要有一定的技巧.教师要尽可能地创设一些处于学生认知发展区内,具有一定挑战性且让学生踮起脚尖才能解决的问题,或需要学生通过合作交流才能获得结论的问题.从心理学的角度来讲,此类问题能真正激起学生的学习动机,从而产生探究行为,为形成严谨的数学思维奠定基础.

例1观察3,6,9,12,15……这组数据,说说它们之间存在怎样的关系.

这组数据对于学生而言并不陌生,在初中阶段即有接触.在学生给出答案后,教师又让学生说说2,4,6,8,10,12……这组数据之间存在的联系.这个问题同样简单,学生表述毫无障碍.接着,教师又提出一个新的问题:“这两组数据之间具有怎样的联系?”学生经观察后,认为:第一组数据相邻两个数的差为3;第二组数据相邻两数之差为2.此时,教师再次提问:这两组数据的第十个数分别是多少?

随着问题的逐渐深入,学生的思维也随着问题呈逐层上升趋势.通过对一个个问题的表述,学生很快就自主抽象出等差数列的概念,进而得到等差数列的通项公式:an=an+(n-1)d.

紧接着,教师又提出以下问题串,要求学生逐个表述:

(1)分别说说两组数据的前五项的和及计算方法.

(2)大家想想,有没有更简单的计算方法?

(3)怎么计算前n项的和呢?

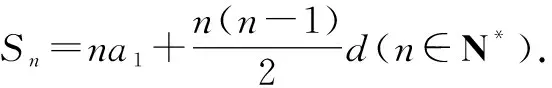
由浅入深的问题诱导,使得学生的思维跟着一个个问题拾级而上.从对最简单问题的表述到公式推理的形成,一环接一环,严谨而又周密,学生的思维也呈螺旋式上升.此过程除了以阶梯状的问题贯穿外,学生的表述也是重点,随着表述越来越完整,学生的思维也越来越严谨,久而久之,学生也对学习也充满了信心.

其实,这种诱导方式除了能锻炼学生的表达能力、严谨思维之外,在一定程度上还激发了学生的探究欲.学生在自我推导与合作学习中,对问题展开相应的研究与推断,这为培养学生的自主学习能力及核心素养奠定了基础.

2 适当引导,严密推理

教学时,一般是将一个个知识点分解到课堂中逐个讲解,这种教学方式体现了知识的独立性.但这种模式也导致了部分学生不会进行知识间的联系,出现思考问题方向单一、思维僵化、缺乏灵活性等现象,这些现象严重地削弱了学生思维的延伸性与系统性.我们知道,数学是一门系统性很强的学科,所有的知识点都不是孤立存在的,知识的前后有着紧密的联系,难度呈递进式上升,学科与学科之间也有着千丝万缕的关联.

因此,教师应有意识地引导学生感知、感悟知识间的这种递进关系,让学生从多层面或多维度去面对问题,实现解题.如此,可培养学生形成联想式的思考模式,在思考与探讨中获得严谨的数学思维.

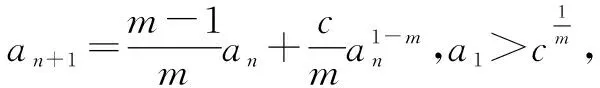
学生看到此题,首先考虑到数列,却不知从何处下手.

师:通过问题中的指数,大家能联想到什么?问题中有哪些量随着其他量的变化而发生变化?

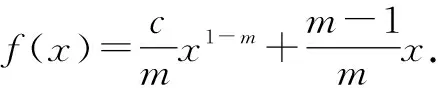
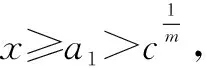
不少学生做到此步,思维卡壳了.教师提醒学生再回过头来看看,待求证的是什么?

有什么办法能证明an>an+1呢?教师提出:求证一个命题的真伪,一般可采取数学归纳法或反证法,本题该选择哪种方法呢?

学生一致选择了数学归纳法,并顺利解题(过程略).

从本题的教学来看,不仅凸显了教师引导的重要性,还凸显了从多角度思考与分析问题的必要性.解题时,学生通过各个关卡的逐个突破,最后再将各个突破点联系到一起,不仅解决了本题,还有效地锻炼了思维,整个过程逻辑清晰、思路明朗、逐层递进,有效地促进了学生严谨性思维的形成与发展.

3 分类讨论,全面考虑

教学中,我们常发现学生在问题的探讨中,总存在不够全面、顾此失彼的现象,不少学生因为不能整体、全面地分析问题而导致丢分.为了巩固和提高学生的逻辑性,可有针对性地利用一些试题来训练学生的思维,让学生结合实际情况,从问题的多角度进行分析与探讨.教学中,笔者常用蕴含分类讨论思想的问题,来激发学生全面思考的能力,以帮助学生更好地形成周密性思维.

例3设函数f(x)=x2+ln(a+x),若f(x)有极值,求a的取值范围.

方程2x2+2ax+1=0判别式Δ=4a2-8.

①当Δ<0时,f(x)无极值.

②当Δ=0时,f(x)也无极值.

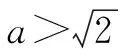
本题充分体现了分类讨论思想的“化整为零”和“集零为整”的策略,揭示了分类对象需清晰、标准统一,杜绝重复、遗漏、越级等原则,将思维的严谨性充分展现出来.因此,分类讨论不仅能带动学生从问题的全面性去思考,还能帮助学生缜密思维,提高认识,提高数学核心素养.

总之,纸上谈兵终觉浅,只有真正地参与并亲历实践,才能不断地自我突破,实现优化、修正原有的固化思维.教学中,教师可充分发挥引导功能,引导学生从多角度出发,周密、严谨思考问题,培养学生形成良好探究习惯的同时,帮助学生养成能促进其终身可持续发展的思维品质.