“不同函数增长的差异”教学实录
⦿ 新疆生产建设兵团第二师华山中学 周振梅
1 教学分析
1.1 教学目标
(1)比较底数大于1的指数函数、对数函数与斜率大于0的一次函数增长的差异.
(2)由特殊到一般归纳出不同函数增长快慢的基本方法.
(3)通过三种函数在不同阶段增长的快慢变化,却在某点之后趋势明显,借以说明做事不为眼前,要立足长远.
1.2 教学重难点
教学重点:学会比较不同函数增长快慢的一般方法.
教学难点:理解变化率在刻画不同函数增长快慢的意义.
1.3 学情分析

2 教学过程设计
2.1 创设情境,引入新课
问题你有一笔资金用于投资,现有两种投资方案供你选择,这两种方案的回报如下:
方案一:第一天回报5元,以后每一天比前一天多回报5元.
方案二:第一天回报2元,以后每天的回报比前一天翻一番.
如果让你选择,你会选择哪种投资方案?
生:时间较长,我会选择方案二;时间较短,我会选择方案一.
师:为什么?
生:因为方案二的日回报增长量会比方案一快.
师:请列出7天的回报量进行比较.
师生活动:学生尝试列出7天的日回报量和累计回报量.教师巡视观察,请同学分享学习成果.
学生列出表1与表2.

表1 日回报量

表2 累计回报量
追问:有同学说时间短选方案一,时间长选方案二,时间长短的选择在表格中有体现吗?
生:由表2可知,前5天方案一的累计回报量高于方案二,但是5天以后方案二的累计回报量高于方案一,且方案二增加的速度越来越快.
追问:方案二的增加速度越来越快,从哪里体现?
生:由表1可看出,方案二日回报量的增加速度在5天后远大于方案一,所以累计回报量就会更多.
追问:从日回报量的角度分析,有哪些函数模型?
方案一对应的函数模型是一次函数,方案二对应的函数模型是指数函数.
教师总结:一次函数和指数函数的增长方式存在很大差异,它们是不同类型现实问题具有不同增长规律的反映.把握了不同函数增长方式的差异,就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.
2.2 数形结合,探索新知
探究1:研究函数y=2x和y=2x,探索它们在区间[0,+∞)上的增长差异.
师生活动:小组合作探究,解决问题.
学生交流的问题大致如下:
(1)为什么在区间[0,+∞)上探究?
(2)以什么路径展开研究?
(3)如何探究两个函数的增长差异?
(4)如何用数学符号语言准确表述它们的增长差异?
生:(1)[0,+∞)有实际意义;(2)利用数形结合进行研究;(3)通过数据的计算及观察图形研究.
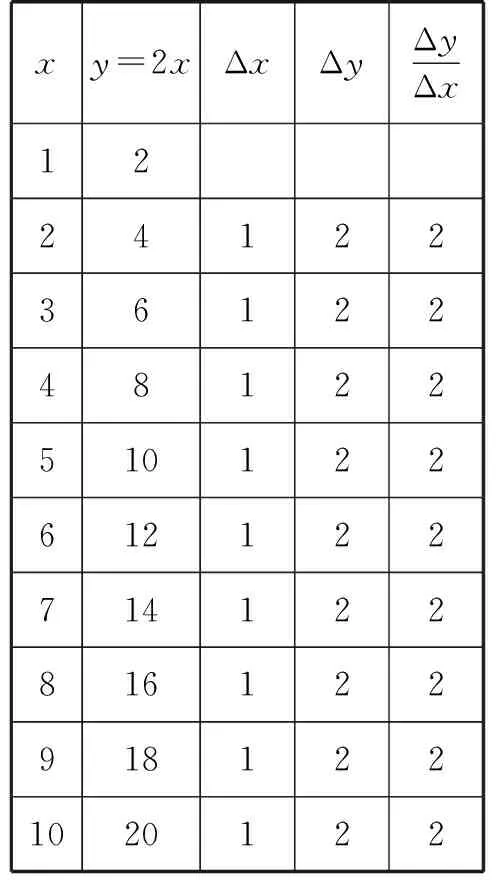
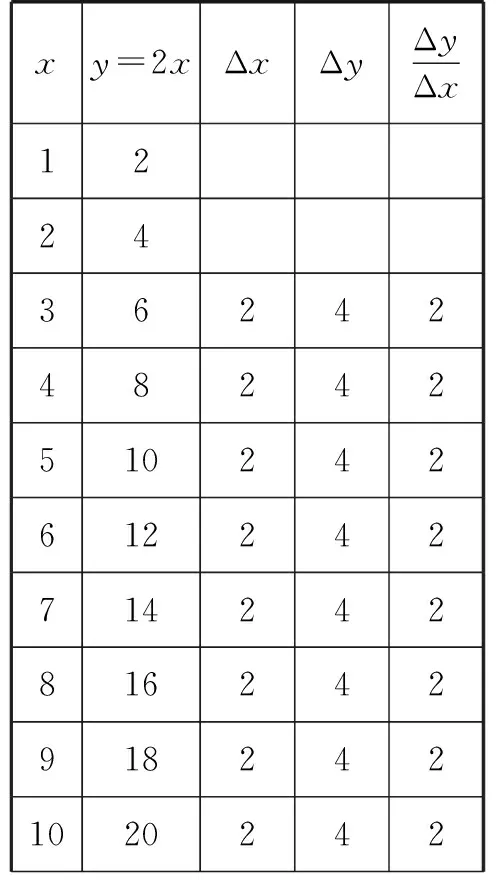
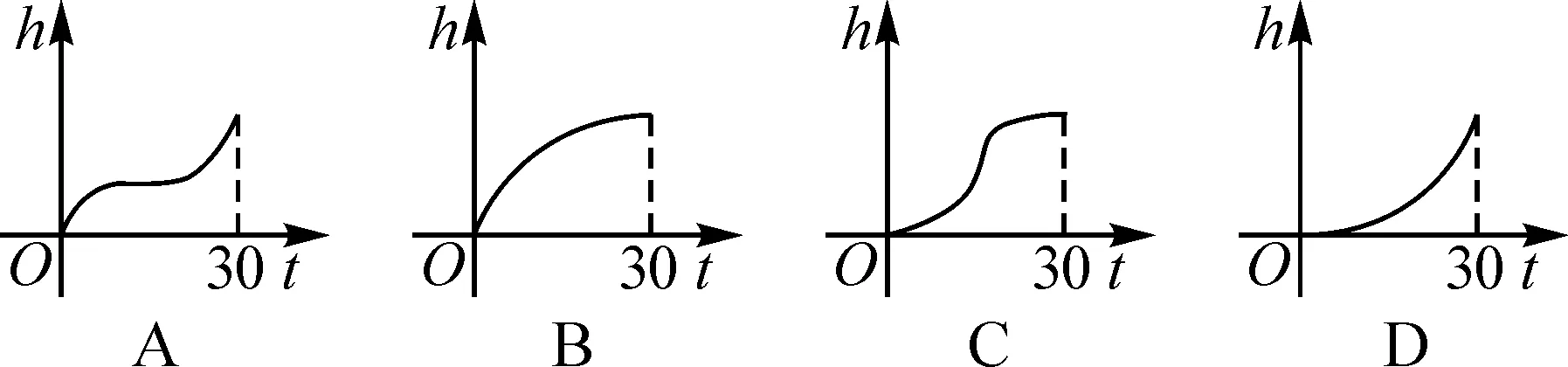
生:观察表格和图象可以发现——一次函数是一条直线,指数函数的图象是一条曲线;共有两个交点(1,2)和(2,4).当0 追问:对于上述情况,还可以从哪个角度进行分析? 生:列表从数的角度分析增长速度. 追问:怎么刻画增长速度?在物理中学习了平均速度,通常用Δv表示,那么怎么定义Δv? 生:物理课上,用平均速度来描述物体在一定时间内位移的改变量.平均速度是指在一段时间内,物体所经过的位移与这段时间的比值.通过比较不同时间段内的平均速度,可以刻画出物体位置改变的速度,也就是增长速度. 师:数学中怎么刻画增长速度? 生:用一定范围内函数值的增加量刻画增长速度.例如,自变量每间隔一个单位长度,一次函数y=2x的函数值相差2,指数函数的函数值差值则越来越大. 师:表3中,你能看出一次函数的增长速度吗? 表3 生:一次函数的增长速度是一个定值,指数函数的增长速度一直在变大. “形”的角度比较:在同一坐标系中画出y=2x和y=2x的图象(如图1),演示y=2x与y=2x增加量的变化情况,提示学生观察自变量的增加量相同时函数值的增量Δy的变化特征,如表3、表4所示: 图1 表4 活动:请小组讨论,归纳这两个函数在[0,+∞)上的增长差异. 生:(1)函数y=2x与y=2x在[0,+∞)上都单调递增,但它们的增长速度不同,而且不在一个“档次”. (2)随着x的增大,y=2x的增长速度越来越快,会超过并远远大于y=2x的增长速度. (3)尽管在一定范围内,2x<2x,但由于y=2x的增长速度最终会大于y=2x的增长速度,因此总会存在一个x0,当x>x0时,恒有2x>2x. 师:什么叫做“爆炸式增长”?它的增长速度有没有特点? 生:它是翻倍式的增长. 师:能否推广到一般情况? 生:一般地,指数函数y=ax(a>1)与一次函数y=kx(k>0)的增长情况与上述情况类似.即使k值远远大于a值,y=ax(a>1)的增长速度最终都会超过y=kx(k>0)的增长速度. 探究2:类比探究指数函数与一次函数的增长差异,你可以探究出对数函数与一次函数的增长差异吗? 学生类比探究1探究对数函数与一次函数的差异. 师:你们组观察得非常细致,从图象交点个数及不同区间上两个函数的函数值大小关系进行了总结.一次函数与指数函数的增长特点是什么? 生:一般地,虽然对数函数y=logax(a>1)与一次函数y=kx(k>0)在(0,+∞)上都是单调递增,但它们的增长速度不同.随着x的增大,一次函数y=kx(k>0)保持固定的增长速度,而对数函数y=logax(a>1)的增长速度越来越慢.不论a值比k值大多少,在一定范围内,logax(a>1)可能会大于kx,但由于logax(a>1)的增长会慢于kx的增长,因此总存在一个x0,当x>x0时,恒有logax 生:仍然有. 师:对!现在我们分别研究了一次函数与指数函数、一次函数与对数函数的增长特点,如果把这三种函数放在一起研究,它们的增长差异是什么? 生:一次函数和对数函数相比,对数函数有一部分函数值大于一次函数,但是对数函数的增长速率越来越小,所以总有一个x0,当x>x0时,一次函数的函数值恒大于对数函数的函数值.一次函数和指数函数相比,因为指数函数的增长速率越来越大,会有一部分函数值小于一次函数的函数值,但也会像对数函数一样存在一个x0,当x>x0时,指数函数的函数值恒大于一次函数的函数值. 教师总结:随着x的增大,y=ax(a>1)的增长速度越来越大,会超过并远远大于y=kx(k>0)的增长速度,而y=logax(a>1)的增长速度则会越来越慢.因此,总会存在一个x0,当x>x0时,有logax 师:我们比较了三种不同类型函数增长的快慢,那对于同类函数增长的快慢,应该如何去表示呢? 生:可以通过平均变化率去表示. 师:对于一般函数的增长快慢怎么去比较? 生:也是通过平均变化率. 师:那么我们可以通过平均变化率去比较任意两个函数的增长快慢. 练习1如图2中的文物叫做“垂鳞纹圆壶”,是甘肃礼县出土的先秦时期的青铜器皿,其身流线自若、纹理分明,展现了古代中国精湛的制造技术.科研人员为了测量其容积,以恒定的流速向其内注水,恰好用时30 s注满,设注水过程中,壶中水面高度为h,注水时间为t,则下面选项中最符合h关于t的函数图象的是( ). 图2 生:此题问的是壶高和注水时间的变化,观察图形,发现这个壶底部的面积比较小,中部的面积比较大,上部的面积比较小.因为是匀速注水,所以高的变化情况是底部和上部增长快,中部增长慢,因此选择A. 练习2已知三个变量y1,y2,y3随变量x变化的数据如表5: 表5 则反映y1,y2,y3随x变化情况拟合较好的一组函数模型是( ). A.y1=x2,y2=2x,y3=log2x B.y1=2x,y2=x2,y3=log2x C.y1=log2x,y2=x2,y3=2x D.y1=2x,y2=log2x,y3=x2 生:通过今天所学的知识,我们知道指数函数、幂函数及对数函数平均变化率的大小关系,然后观察表格,发现y1,y2,y3的平均变化率依次递减.因此选择B. 练习3有甲、乙、丙、丁四种不同品牌的自驾车,其跑车时间均为x小时,跑过的路程分别满足关系式:f1(x)=x2,f2(x)=4x,f3(x)=log3(x+1),f4(x)=2x-1,则5个小时以后跑在最前面的为( ). A.甲 B.乙 C.丙 D.丁 生:观察函数的形式,f1(x)是幂函数,f2(x)是一次函数,f3(x)是对数型函数,f4(x)是指数型函数,指数型函数平均变化速率是最大的,所以5个小时以后跑在最前面的是丁,故选D;还可以通过计算得当x=5.f4(x)最大,所以也选D. 本节课由特殊到一般、由具体到抽象研究了一次函数y=kx(k>0)、指数函数y=ax(a>1)及对数函数y=logax(a>1)在定义域上的不同增长方式.可以用一首诗来形容本节课:“指对线同时增加,比大小初不确定,喻开始波澜不惊,待将来厚积薄发”. 请同学们赏析这首小诗和本节课的联系. 生:这首诗与本节课内容紧密相关.诗中提到指数函数、对数函数和一次函数在区间(0,+∞)内都单调递增,但最初的增长速度并不能确定未来的趋势.指数函数的增长初缓慢后迅速,超越一次函数.以时间为x,成就为y,能力为平均变化率,时间、能力与成就如同指数函数,即使最初能力不出众,随着时间的推移,能力增长越来越快,未来成就也会越来越大. 师:谢谢,说得非常好!希望同学们因为喜欢数学而学习数学,也因为学习数学而更热爱数学.下课! 注:扫图3可观看课堂视频. 图3 备课时,教师准备用几何板演示三种函教模型的增长差异,这样使得分析更直观.实际上课的时候,由于给学生自主学习和讨论交流的时间较充裕,学生自己总结出了三种函数模型的增长差异,所以没有演示.这样可能会使得结论的说服力不是很强,也失去了一些趣味性.在备课时应尽量宏观考虑,力争做到在有限的时间内取得更佳的教学效果. 语言不够精炼,有些地方重复,有些地方表述不到位.既然给了学生小组讨论的时间,就应该让学生尽可能多展示他们自学和交流的结果,然后根据展示情况进行精讲.没有做到“以学定教”,浪费了一部分时间. 师生的交往互动没有达到很好的状态,虽然学生总体愿意回答,但是引导还不到位,应该更多使用几何画板和Excel处理数据,使教学增加趣味性和说服力.
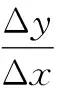

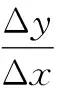



2.3 课堂练习


2.4 课堂小结

3 课堂反思

