基于GPU加速的三维堆芯物理程序STORK的开发与验证

俞陆林,杨高升,陈国华,卑 华,蒋校丰,高明敏,王 涛

(1.上海核星核电科技有限公司,上海 201103;2.核电运行研究(上海)有限公司,上海 200126)

面对越来越复杂的反应堆堆芯和燃料组件设计,目前用于大型商用反应堆堆芯核设计软件受到了挑战,需要开发适用性更广、计算精度更高、计算效率能够满足工程应用需求的堆芯物理分析软件。近年来,国内外对新一代堆芯中子学计算方法展开了广泛研究,如美国和韩国联合开展的I-NERI计划[1-2]、美国的CASL计划[3]、欧盟的NURESIM计划[4]等,国内科研机构也基于不同的输运方程求解算法开发了高精度的堆芯物理计算程序,如基于2D+1D框架的西安交通大学输运计算软件NECP-X[5]、中国核动力研究院的Tiger[6]、KYCORE[7]和KuaFu[8]等,基于三维MOC框架的中国原子能科学研究院的ANT-MOC[9]、清华大学的TCM[10]、哈尔滨工程大学的HNET[11]、ALPHA[12]等,基于2D+3D框架的上海核工程研究设计院有限公司的SCAP-N[13]。

另一方面,随着人工智能领域对算力需求的爆发式增长,基于CPU/GPU异构的系统在高性能计算领域的应用愈加广泛。在反应堆计算分析领域,无论是在基于非确定论方法的计算程序中,如韩国首尔大学的PRAGMA程序[14],还是在基于确定论方法的计算程序中,如上海应用物理研究所的ThorMOC程序[15]、哈尔滨工程大学的ALPHA程序[12]、韩国首尔大学的nTRACER[16]、GPU都开始得到了应用,并且显著提高了程序的计算效率。计算机算力的大幅增长,使得采用高精度的算法求解三维输运方程来满足工程应用需求开始变得可能,其中包括以棒栅为均匀化单位进行全堆芯精细化建模和计算。在此背景下,本文基于GPU加速技术研发了二维MOC耦合三维SP3计算的堆芯物理分析计算程序STORK。该程序首先根据轴向材料布置自动化地对堆芯模型进行轴向分层;针对所有包含活性区的分层,在GPU上并行地开展二维全堆MOC计算,并采用两重非结构化网格粗网有限差分方法(UCMFD)进行加速[17];利用二维全堆输运计算结果在线产生每一层的少群或中间能群形式的栅元均匀化截面以及超级均匀化(SPH)因子[17];对非活性区轴向层,则采用与其相邻的活性区层的能谱产生栅元均匀化截面;最后基于上述步骤获得的均匀化截面及SPH因子进行全堆三维SP3计算,获得有效增殖因数、棒功率分布等堆芯物理参数。

1 理论模型

1.1 多群常数库及共振计算

STORK程序采用多群核数据库RLIB,RLIB是上海核星核电科技有限公司在国际原子能机构“WIMS-D多群常数库更新项目(WLUP)”项目ENDF/B-Ⅶ.0 69群数据库的基础上完善而来的,主要包括:重新制作了铀、钚等重要同位素的截面;增加了钨、铼同位素以及镝等同位素的多群截面及燃耗链信息以满足AP1000和VVER1000反应堆控制棒的计算;扩展了如铀、钚等重要同位素之间共振干涉因子表;补充了独立的俘获释能和裂变释能用来更精确地统计堆芯释热率分布等。

STORK程序采用强化中子流方法[18]与等价理论[19]相结合的方式进行共振计算。强化中子流方法通过构建特殊的固定源问题,采用MOC方法来计算获得反应率,最后由式(1)统计每个共振材料区每个共振能群的Dancoff因子D:

(1)

式中:Rtot为总反应率;Σs,f为宏观势散射截面;Σe为与该共振区平均弦长相关的“逃脱”截面。STORK中不进行显式的Dancoff效应修正计算,而是直接将与位置相关的Dancoff效应体现在二项有理近似展开式中,详细介绍参见文献[20]。另外,为了能够更为精确地考虑共振干涉效应,STORK不再采用传统等价理论中本底迭代的方法,而是通过预先制作好的共振干涉因子表来加以考虑。

1.2 几何处理及输运计算

STORK采用构造实体(CSG)几何建模方式,通过对圆和任意凸多边形这两种内置基本几何体的布尔运算构造各种复杂几何体。如图1所示,像VVER的组件格架及重反射层、十字螺旋燃料棒、板状燃料及十字形控制棒等复杂几何体,STORK都可以精确建模。此外,在几何建模的方式上,STORK遵从严格的面向对象策略,对燃料组件、毒物棒束、控制棒束、围板反射层等三维对象分别建模完成后,再添加位置信息形成最终的三维反应堆。STORK程序具有自动进行网格划分、轴向分层、区域分解等功能,极大地简化了用户输入。

图1 STORK程序的几何处理能力Fig.1 Modeling capabilities of STORK code

STORK求解线性源近似[21]的MOC方程,从而能在更少的离散网格数下达到更高的计算精度,并降低存储开销。STORK采用组件模块化的特征线形式[22],以利用组件模块化特征线存储小、边界可以直接连接等优点。但在特征线产生方式上,不同于传统组件模块化特征线基于组件的方式,STORK基于GPU直接在两维全堆层面上一次性产生全部特征线信息,以提高特征线信息计算过程的并发量。在特征线储存时进行连续存储,不同层次的特征线以指针形式获取,以提高特征线扫描时GPU的合并访存率。

为了提高计算效率同时兼顾方形组件和六角形组件,STORK程序采用适用于任意凸多边形的非规则网格CMFD方法加速MOC方程的收敛[17],并且采用多群和少群双重CMFD加速策略,其中少群CMFD的截面和偏流分别由多群CMFD的截面和偏流压群而来,由少群CMFD求解的注量率则再返回于多群CMFD中。为了能够高效地在GPU上求解,STORK对CMFD线性系统采用雅可比和红-黑迭代相结合的源迭代求解方法。同时,CMFD也采用与MOC完全一致的多层区域分解并行在多个GPU上求解。在具体计算策略方面,由于多群CMFD单次迭代计算量大,只进行固定次数迭代,而少群CMFD单次迭代计算量小、迭代次数多,负责全局问题的收敛。

1.3 在线等效均匀化方法

在线等效均匀化方法中,利用二维全堆MOC计算(轴向采用全反射边界条件)得到各活性区轴向层的中子注量率能谱,产生栅元均匀化少群截面参数,并迭代产生超级均匀化修正因子(SPH因子):

(2)

(3)

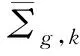
对于处于堆芯顶部和底部的反射层,直接利用与它相邻的活性区层的中子注量率能谱来产生栅元均匀化截面,而SPH因子则设为1.0。

1.4 三维堆芯pin-by-pin SP3方法

SP3理论由球谐函数(PN)方法简化而来,相比于扩散理论,能够对输运理论做出更好的近似,能够兼顾计算精度和计算效率,是三维全堆pin-by-pin计算的理想选择。STORK程序中三维SP3求解器采用了赵荣安提出的SP3方法[24-27]的方程形式:

患者眩晕症状全部消失，不影响患者的正常工作及生活，随访2个月无复发评价为显效；患者眩晕症状有显著改善，头疼现象有明显减轻，随访2个月发作频率较之前有明显减少评价为有效；达不到上述标准者评价为无效。临床总有效率=显效率+有效率。

(4)

(5)

(6)

(7)

(8)

式中:Σ0,g为移出截面;Σt,g为总截面;Qg为中子源项;χg为裂变谱;keff有效增殖因数;vΣf,g为裂变中子产生截面;Σs,g′g为能群g′到g的中子散射截面;F0,g为零阶中子注量率;F2,g为二阶中子注量率。

在该SP3方程形式下的边界条件为:

(9)

(10)

(11)

(12)

对于方形节块问题,STORK程序采用半解析展开节块法求解SP3方程[28]。STORK程序首先采用横向积分技术将三维SP3方程分解为3个一维SP3方程进行求解,通过横向泄漏项进行耦合。对于每个一维方程,对节块横向积分注量率采用多项式或半解析展开式进行近似,利用节块面偏流连续等条件定解展开式系数。具体而言,考虑到STORK应用于三维全堆pin-by-pin计算,在径向方向,节块尺寸较小,横向积分中子注量率采用抛物线展开,利用节块表面平均入射流、出射流连续的条件进行定解;而在轴向方向,节块尺寸较大,横向积分中子注量率采用半解析展开,除了节块面平均入射流、出射流地连续性条件,还需引入一阶矩权重和二阶矩权重的条件,以确定所有展开系数。对于中子源项,采用抛物线近似,横向泄漏项通过三节块法确定其展开式。为了提高三维pin-by-pin计算的效率,采用粗网有限差分方法加速本征值和注量率的收敛。

在STORK的SP3计算模块中,根据GPU的数据读取特点和计算特性,采用统一内存管理的方式,合理设计数据存储结构和算法,最大限度地发挥GPU的计算性能。在算法层面,在求解SP3方程时,采用单节块扫描方式,即给定节块面平均入射注量率,通过求解单个节块内的三维SP3方程,得到节块内各方向的横向积分注量率展开式及节块体积平均注量率,从而确定节块各面的平均出射注量率,在下一次计算前并行地更新所有节块的面平均入射注量率,这种单节块扫描方式可最大限度增加算法的可并行度,此外,结合SP3方程求解算法,STORK基于合并访存的理念,合理设计数据的储存结构,以提高程序计算效率。

2 程序实现

STORK程序采用CUDA、C++、Python三种语言混合编程。所有计算相关模块,如共振计算、输运计算、CMFD加速、燃耗计算等都采用CUDA编写,几何建模、日志信息管理、计算结果编辑、输入输出等模块采用C++编写,而模型及结果可视化则使用Python编写,充分发挥不同编程语言的优势。

STORK程序以单台多GPU的深度学习服务器为开发计算平台,在CPU端采用OpenMP并行技术,GPU端采用基于CUDA Unified Memory的多GPU并行技术。为了尽可能提高计算效率,STORK中的计算流程中,包括MOC、CMFD、共振计算、燃耗计算、SP3计算模块中的计算部分都放在GPU端(图2),并且采用统一的轴向网格划分,单个GPU计算连续的多层,以减少GPU间的数据传递开销、提高并发量。此外,由于采用CUDA Unified Memory技术,自动实现GPU端和CPU端的数据迁移,并且能够在GPU显存不够的情况下,以内存作为补充来模拟超大规模问题,如大型商用压水堆堆芯问题。

图2 STORK计算流程Fig.2 Calculation flow of STORK

为了提高程序的计算效率,STORK程序在性能优化方面做了大量工作,例如:精细设计每个计算模块的主要数据结构,特别是散射矩阵、燃耗矩阵等,使其存储方式能够满足GPU线程最大限度的合并访存;采用大数组与指针相结合的方式来满足面向对象程序设计的同时又能够高效地进行大规模内存的分配和回收;根据GPU硬件设计特点,如GPU的寄存器、共享内存、常量内存等多级存储架构,合理设计程序算法,采用中间变量在线计算等方式,尽量减少全局内存的访问次数;采用CUDA内建的指令级优化的数学函数,如指数运算、除法运算等;采用基于多个Stream同时并发的方式来重叠计算与数据传输的时间;在Unified Memory架构下的多GPU并行时采用DataPrefetch等手段减少数据传递开销。

3 数值验证

本文选取三维C5G7插棒基准题和美国轻水堆数值反应堆项目(CASL)中的VERA系列基准例题[29]对STORK程序进行数值验证,以验证程序的计算精度及性能。

3.1 C5G7-MOX插棒基准题

C5G7-MOX插棒基准题[30]是OECD/NEA于2005年发布的用于检验输运计算程序求解非均匀堆芯问题数值精度的基准问题。由于它的组件能谱差异较大、非均匀性较强,被国际研究机构广泛用于堆芯计算方法的检验。三维C5G7-MOX插棒基准题包含两个插棒子问题,插棒问题A(C5G7-Rodded-A)和插棒问题B(C5G7-Rodded-B)。

本文中基准题的参考解由OpenMC[31]计算产生。STORK和OpenMC都采用1/4堆芯建模,OpenMC共计算了2 000代,其中后1 500代计入统计,每代投入的粒子数为200 000个。SROTK计算MOC采用线性源近似,单个象限极角数目为2个,方位角数目为8个,特征线密度为0.03 cm,轴向每层3.57 cm,共分为18层。

该基准问题的计算在配有1张NVIDIA GeForce RTX 3090显卡的计算平台上完成。STORK程序的计算结果见表1和图3。在计算效率方面,C5G7-Rodded-A问题和C5G7-Rodded-B问题的计算时间分别为8.90 s和9.95 s。

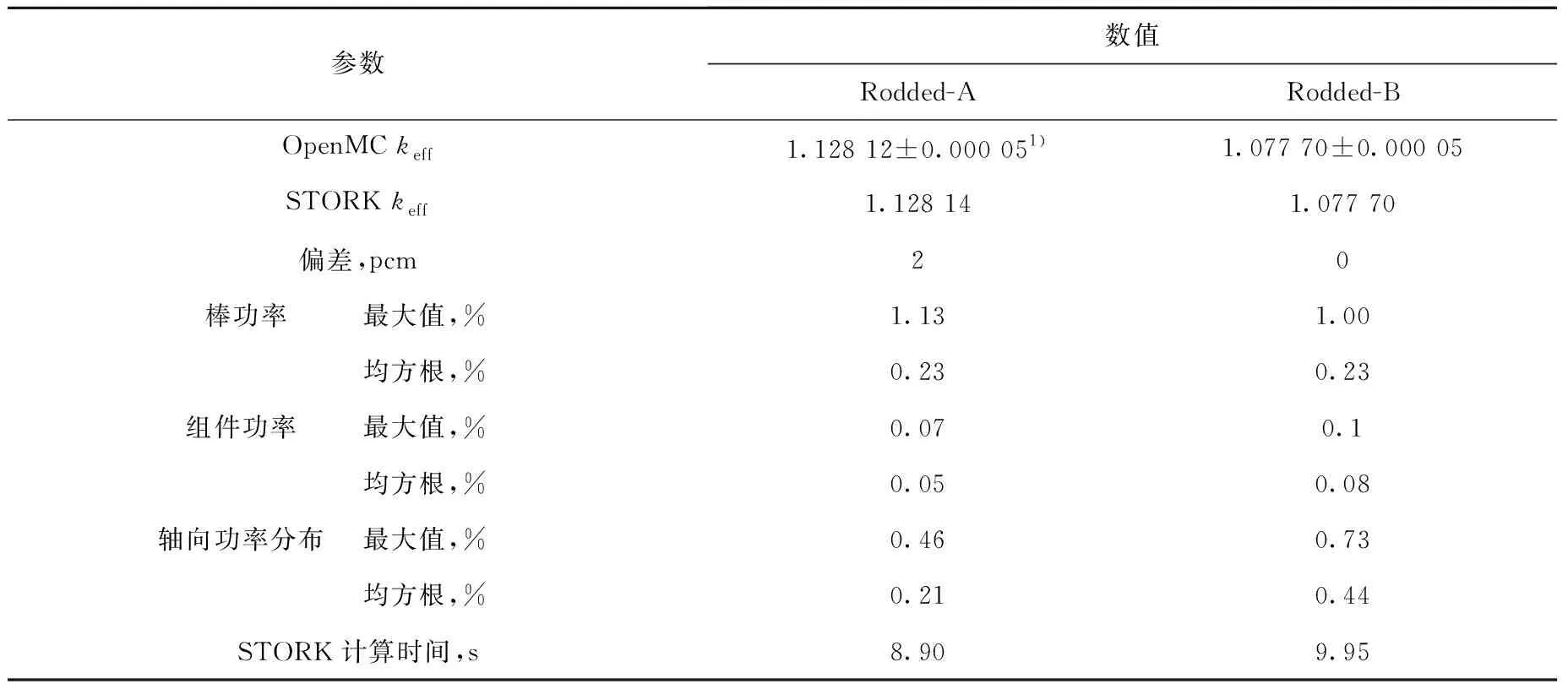
表1 C5G7插棒基准题计算结果Table 1 Result for C5G7-Rodded problem

图3 C5G7-Rodded-A(a)和C5G7-Rodded-B(b)栅元径向功率相对偏差分布Fig.3 Radial pin power relative error distributions for C5G7-Rodded-A (a) and C5G7-Rodded-B (b)

3.2 VERA#3三维基准题

VERA #3基准问题是一个三维HZP BOC状态下的燃料组件问题,主要用于验证程序在没有热工反馈和燃耗下有效增殖因数以及棒功率分布的计算精度[29]。该基准问题包含A和B两个子问题,参考解由蒙特卡罗程序KENO-Ⅵ计算产生。

限于篇幅,本文仅给出VERA #3A问题的验证结果。图4为STORK程序所建的VERA基准问题#3A模型,STORK计算得到的本征值为1.175 32,与参考解的偏差为-40.0 pcm。图5、6分别为棒功率分布和轴向功率分布与参考解的比较。从结果看,STORK程序计算得到的径向棒功率分布与KENEO-Ⅵ的计算结果相比偏差较小,最大偏差在0.2%以内。但轴向功率分布在局部位置出现了较大偏差,达到3%,出现在靠近底部反射层的位置,并且在活性区内部格架位置也出现了较大偏差,接近2%。这主要是因为目前STORK程序中轴向反射层直接采用了与其相邻层的活性区的能谱,而内部格架位置处的轴向层未考虑相邻轴向层的中子泄漏对其能谱的影响。后续将开展针对性的研究以解决这些问题。

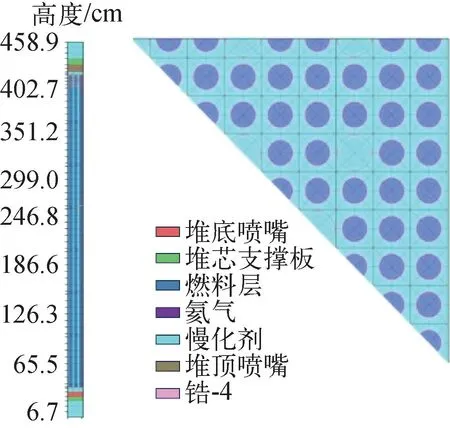
图4 VERA基准问题#3A的STORK模型Fig.4 STORK model for VERA benchmark #3A

图5 VERA基准问题#3A STORK和KENO-Ⅵ的棒功率分布相对偏差Fig.5 Deviation of pin power distributions between STORK and KENO-Ⅵ for VERA benchmark #3A

图6 VERA基准问题#3A STORK和KENO-Ⅵ的轴向功率分布及偏差Fig.6 Axial power distribution and deviation between STORK and KENO-Ⅵ for VERA benchmark #3A

该基准问题的计算在配有2张NVIDIA GeForce RTX 3090 GPU显卡的计算平台上进行,STORK的计算时间为29.39 s,相比于KENO-Ⅵ在240核的计算平台上的计算效率(耗时120 h)具有明显优势,国际同类计算程序的计算时间约为390 s[5]。

3.3 VERA#5三维基准题

该基准例题[29]堆芯共由193盒燃料组件组成,除堆芯活性区外,还包含了围板、吊篮、中子屏蔽体和压力容器等堆外结构,如图7所示,A、B、C、D为调节棒组,SA、SB、SC、SD为停堆棒组。

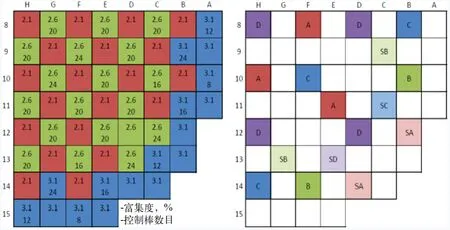
图7 VERA#5三维基准题堆芯燃料和控制棒控制图Fig.7 Fuel and control rod configuration for 3D VERA#5 benchmark

该基准例题按硼浓度、温度及控制棒棒位等不同堆芯工况分为32个算例,其参考解也由KENO-Ⅵ产生。限于篇幅,本文仅给出算例1的STORK验证结果。

该基准问题的计算在配有10张NVIDIA GeForce RTX 3090 GPU显卡的计算平台上进行,STORK的计算时间为399 s,相比于KENO-Ⅵ在180核的计算平台上的计算效率(耗时约696 h)具有明显优势。

在计算精度方面,STORK计算的keff为0.999 98,与KENO-Ⅵ的偏差为-2 pcm,组件功率分布及偏差如图8所示。其中,组件功率的最大偏差仅为-0.75%。

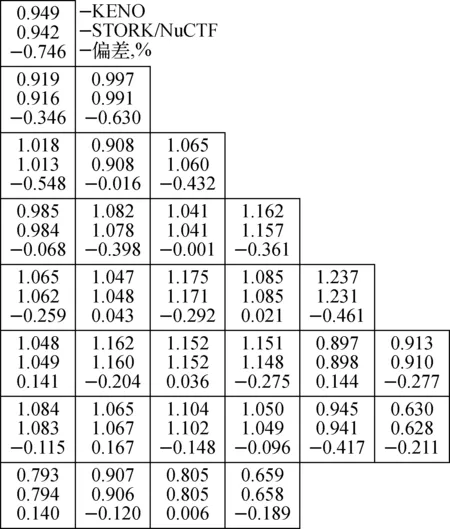
图8 VERA#5基准题算例1组件功率分布计算结果Fig.8 Assemble power distribution for case 1 of VERA#5 benchmark

上述基准题的计算结果表明,与国际上采用高性能CPU集群平台开发的其他中子学计算软件相比,基于CPU/GPU异构系统开发的、运行与单机服务器上的STORK程序所用的计算时间更少,针对大型压水堆堆芯,STORK程序单个状态点计算时间为数百秒,折合能耗不到1 kW·h(配有10张NVIDIA GeForce RTX 3090 GPU显卡的计算平台功率为4.0 kW),而高性能CPU集群平台的计算能耗,以天河超算平台为例,约为0.5 (kW·h)/核时,基于高性能CPU集群平台的中子学计算软件的计算时间为数十至上百核时不等[13],折合能耗为数十至上百千瓦时,由此可见STORK程序所花费的计算成本更低,即使考虑单机服务器的购置成本(本文所采用的10张NVIDIA GeForce RTX 3090 GPU显卡的计算平台购置成本约为20万元),STORK程序的综合计算成本也小于基于高性能CPU集群平台开发的中子学软件。

4 结论

本文基于CPU/GPU异构系统并采用二维MOC与三维SP3相耦合方法开发了堆芯物理计算程序STORK。同通过对C5G7-MOX插棒基准题和VERA#5基准问题的验证结果表明,STORK程序能够获得较高的计算精度。与国际上采用高性能CPU集群平台开发的同类中子学计算软件相比,基于CPU/GPU异构系统开发的STORK程序在计算效率和计算成本方面都具有明显的优势。

目前研究已完成了STORK程序与同样基于CPU/GPU异构系统开发的子通道程序NuCTF的耦合,并开展了带热工反馈的国际基准问题以及国内VVER-1000机组和M310机组等多个燃料循环的验证,这些工作将在后续文章中加以介绍。