温度对组合型织构油封密封性能的影响

张志祥，张付英，夏靖炜，马骏，刘元刚

(1.天津科技大学机械工程学院，天津 300222；2.天津市轻工与食品工程机械装备集成设计与在线 监控重点实验室，天津 300222；3.天津市科技发展服务中心，天津 300000)

油封因具有阻止设备内润滑油外泄和防止外界污染物进入装置的功能和结构简单的特点，被广泛应用于工业领域。油封在动态运行过程中，可在密封件和轴之间产生几微米厚的承载油膜，有助于减少摩擦和磨损，延长密封系统的使用寿命。油封的反向泵送效应可防止润滑油从密封接触区域向空气侧逸出，因此通过设计宏观或微观的流体力学特征，也称为泵送结构，如肋、螺旋、织构、涡轮模式或密封辅助装置等，均可增强反向泵送效应，提高密封效果，延长密封寿命。

目前已经证明，在气缸活塞环、轴承滑块、机械密封等机械元件表面添加设计良好的表面织构可以改善润滑条件下的摩擦学性能[1-3]，定向纹理[4-5]如椭圆形、三角形、矩形等形状的微凹坑等，具有显著的控制泄漏的能力。OTTO和PATERSON[6]最先在旋转油封中应用表面织构技术。HADINATA和STEPHENS[7]用数值分析方法研究了微观织构对唇形密封的弹性流体动力学效应。WARREN和STEPHENS[8]通过一系列油滴试验表明，带有微三角形凹坑的轴可以减少径向唇形密封的摩擦扭矩和泄漏。在过去的10年中，学者们深入研究了表面织构形态对旋转唇形密封性能的影响。JIA等[9]提出了一种静态弹性流体动力学模拟方法，分析了斜槽轴对泵送作用的影响，并通过实验验证了所提出的模型；数值和实验结果都表明，凹槽可以显著提高泵送速率。基于相同的理论模型，GUO等[10]分析了接触区的轴向位置对轴表面具有不同微凹坑纹理形状(圆形、方形和三角形)的唇形密封性能的影响。LI等[11]对旋转唇形密封件进行了数值分析，将该密封件与带有微三角形凹坑的轴接触，获得的反向泵送速率与实验结果基本一致。ZHANG等[12]也对具有表面纹理的油封进行了数值分析和计算，表明唇部表面纹理技术的应用对油封的油膜厚度、摩擦扭矩和泵送速率有明显影响。为了探索轴粗糙度对旋转唇形密封性能的影响，EL GADARI等[13-14]提出了全膜润滑下旋转唇形密封的数值EHL模型，并考虑了轴和密封唇粗糙度的影响，结果表明，当轴粗糙度超过唇缘粗糙度的1/2时，密封件可能会泄漏；之后，他们在轴表面添加斜槽，以提高泵送速率，并进一步研究了纹理轴对旋转唇形密封磨损的影响。

作者前期也研究了组合型表面微织构对油封密封性能影响，证明了组合型织构对油封油膜厚度以及泵吸率的提升都有显著效果[15]。为了探究温度对组合织构油封的影响，本文作者通过有限元与数值模拟相结合的方法研究具有表面组合型织构的油封在接触区域的温度分布，以及唇口温度变化对油封密封性能的影响。

1 油封结构及有限元模型

1.1 油封的结构

油封的密封系统由3个主要部件组成：轴、密封圈和润滑剂，如图 1所示。以唇尖作为分割点，右侧为油液侧，左侧为空气侧。以某变速器输入轴外伸端轴承的油封为研究对象，其型号为60 mm×80 mm×8 mm，主体材料为丁腈橡胶(NBR)，内有金属骨架支撑，外有紧固弹簧，过盈量为0.3 mm，油侧唇角为45°，空气侧唇角为25°。

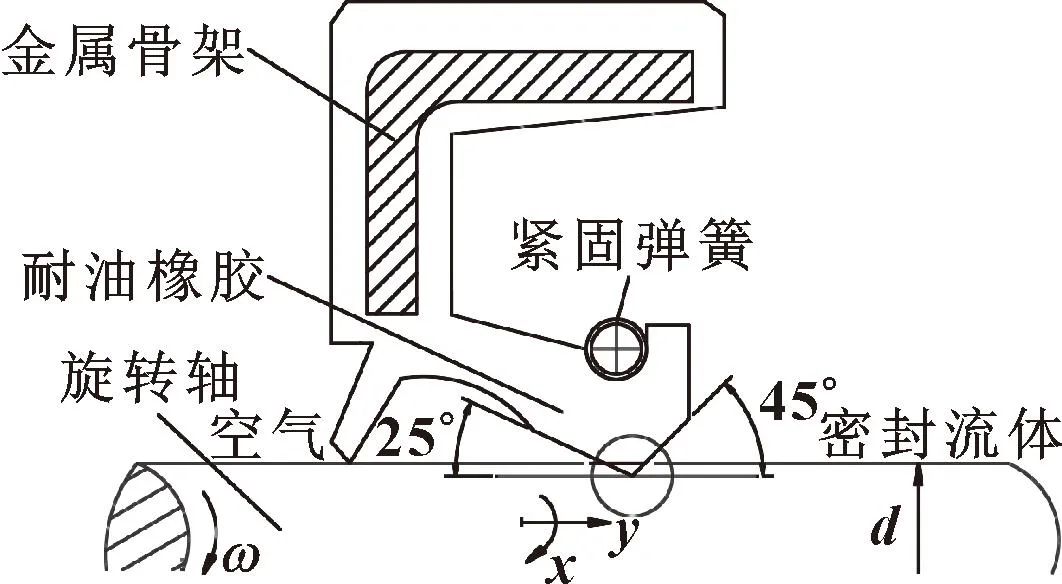
图1 油封密封系统示意Fig.1 Schematic of an oil seal sealing system

1.2 油封表面微观织构的组合设计及其参数

大部分油封的表面微观织构采用十字状、线状、三角形、正方形、圆形等单一几何形状。由于不同几何形状对油封的泵吸率、膜厚等影响程度存在差异，因此将不同织构形状进行组合设计，可综合2种不同织构的优点，使其在密封的润滑特性和密封特性方面都具有积极贡献。

在前期等边三角形、正方形和圆形表面微观织构对油封密封性能影响研究的基础上，将三角形、圆形和正方形3种微织构的形状进行相互组合设计，得到如图2所示3种新的组合型表面微观织构形状。

图2 表面织构示意Fig.2 Schematic of surface textures：(a) texture A； (b) texture B；(c) texture C

新设计的组合型微凹织构，均匀地加工分布在唇端两侧，如图3所示为微观组合型织构的分布。织构参数设计是以面积相近为原则，考虑到制造精度以及经济性，对于仅0.29 mm的接触宽度，数十微米范围的纹理比例是合理的，其具体参数见表1。

图3 油封唇部微观织构分布Fig.3 Texture distribution of oil seal lip

表1 织构参数单位：μm

1.3 油封的有限元模型

为获得油封静态接触压力以及径向变形影响系数矩阵，需建立油封的有限元模型。为保证结果准确度和快速求解，建立油封的有限元模型时做出如下假设：

(1)旋转轴与油封骨架为刚性材料；

(2)油封为轴对称模型且其运行过程保持静止；

(3)忽略模型运行期间，温度、黏弹性、材料密度随时间变化的影响，认为其为常数。

油封材料及建模参数如表2所示。丁腈橡胶的应力应变性能是通过二项参数的Mooney-Rivlin模型来描述，其中常数项C10=0.994 MPa，C01=0.236 MPa[16]。划分网格时，骨架、旋转轴以及紧固弹簧采用C3D8R，油封采用C3D10M，织构区域单独处理进行网格细化，以保证计算精度及结果的准确性，油封的有限元模型分别如图4和图5所示。

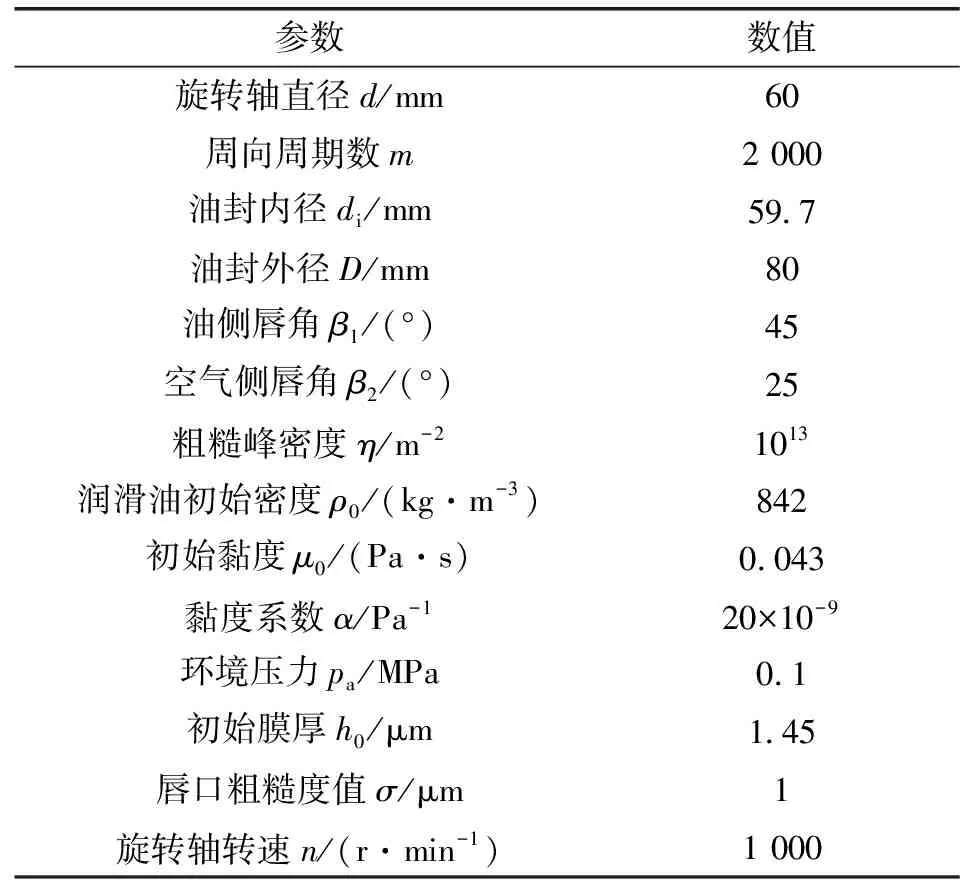
表2 油封模型基本参数

图4 油封有限元模型Fig.4 Finite element model of oil seal

图5 油封唇口局部织构Fig.5 Partial texture of oil seal lip

2 油封的数值计算模型

图6所示为给定的圆周位置密封区示意图。假设轴是完全光滑、刚性和旋转的，而密封唇被视为粗糙、弹性和静止的。由于膜厚度远小于密封半径，因此使用笛卡尔坐标系，并将坐标系固定在轴上，以使问题稳定。x、y分别表示圆周和轴向坐标，为了计算反向泵送速率，假设密封件的空气侧充满液体。建立油封的数值模型时，假设唇部是轴对称的，且唇部表面微凸体的微变形不影响唇部的宏观变形。

2.1 流体力学分析

流体力学由雷诺方程和质量守恒边界条件 (JFO 条件)控制。油封工作时，当油膜压力低于溶解气体饱和蒸气压时，会发生空化。因此空化指数F和通用变量Φ用于说明这种影响。具有流量因子的通用平均雷诺方程为

(1)

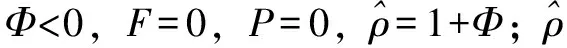
边界条件为：Y方向，PY=0=Psealed，PY=1=1；X方向P周期性变化，即PX=0=PX=1，所有节点位置P≥0。

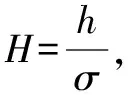
φx=1-0.9e-0.56H，φy=1-0.9e-H/0.56

(2)

剪切流量因子φs表示微观表面上受流体的滑动影响，是额外流量因子，计算公式为

当H≤5时，φs=1.899H0.98e-0.92H+0.05H2；

当H>5时，φs=1.126e-0.25H。

2.2 接触力学分析

当膜厚低于表面粗糙峰高度时，密封区域必然存在粗糙峰接触，接触压力效应显著，必须考虑。采用Greenwood-Williamson(G-W)表面接触模型求解粗糙峰接触压力Pc，其计算公式为

(3)

式中：η为粗糙度密度；ξ是集成的虚拟变量；在G-W模型中，所有接触粗糙体都被认为是具有相同曲率半径Rseal的球形凸体集合，其高度具有一定的统计分布；E′表示组合弹性模量，但由于文中将轴视为刚性，E′只是弹性体唇缘的“平面应力模量”，其计算如式(4)所示。

(4)

式中：ν为油封唇口泊松比；E为唇口弹性模量。

φ(z)是密封唇表面粗糙峰高度分布的概率密度函数，当密封唇表面遵循高斯分布时，由式(5)计算。

(5)

σs表示粗糙度高度的标准偏差，其与粗糙度σ之间的关系为

(6)

油封唇口的随机粗糙表面可通过密封唇表面高度分布的概率密度函数φ(z)和自相关函数c(x，y)来描述，自相关函数表征沿表面的凹凸的横向分布，高斯分布的自相关函数如式(7)所示。

(7)

式中：λx和λy分别表示x、y方向上的相关长度，文中取λx=13.7，λy=29.6[17]。

图7所示为数值生成粗糙表面截面的示例。

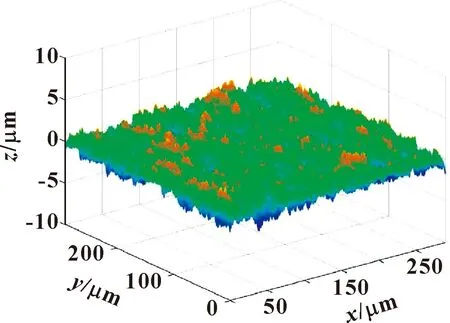
图7 唇口粗糙面数值模拟Fig.7 Numerical simulation of the rough surface of lip

2.3 变形力学分析

变形力学分析用于计算密封的凹凸的变形形状，为了获得密封件的变形，采用了影响系数法。该方法的有效性基于2个假设：(1)在整个计算过程中，密封的刚度被视为不变；(2)根据小变形理论，假设在密封区，任何位置的变形与每个位置施加的力成比例。

使用商业软件包Abaqus，通过有限元分析获得影响系数矩阵(I)ik以及静态接触压力Psc，进而求得润滑区域的油膜厚度。油膜厚度由式(8)求得。

(8)

式中：Hw为纹理结构参数，是将织构深度及形状尺寸编辑为100×100的矩阵形式代入油封变形公式中；Hs为静态油膜厚度；Pt为总压力，由式(9)求得。

Pt=Pc+Pavg

(9)

式中：Pavg为平均流体压力。

2.4 油封唇口温度数值模型建立

在密封处，随着轴的转动，摩擦会产生热量。一部分热量通过油封与轴传导，另一部分被润滑油带走(对流)。因此，润滑油温度会因产生的热量而升高。温度升高会影响润滑油的密度和黏度。特别当润滑油处于低温条件时，温度的微小上升会导致润滑油黏度的显著变化。由于润滑油黏度对温度变化非常敏感，因此使用基于能量方程的分析方法来计算润滑油的温度分布。通常，考虑油膜中的黏性耗散加热效应，三维稳态能量方程可以表示为

(10)

式中：T是润滑油温度；U、V分别是x和y方向上的流体速度，油膜中相应的速度根据Navier-Stokes方程计算，用有限差分法求解，此处不再赘述，可参阅文献[18]；Z是径向坐标，参数k、βT和cp分别是润滑油的导热系数、热膨胀率和比定压热容。

在式(10)中，左侧表示对流与热量传导，右侧分别表示黏性耗散和压缩加热。此外，当膜厚过小时，应考虑粗糙峰接触对生热的贡献。粗糙峰接触对生热Qasp由式(11)计算。

(11)

式中：kasp为摩擦因数。

在方程(10)的求解过程中，油封和轴的表面温度尤为重要。润滑油带走了一部分热量，其余部分则通过边界接触面进行传热。流向表面的热流决定其表面温度，进而调节润滑油温度。根据YANG等[19]的研究，表面温度可以通过如式(12)所示的油封传热方程、式(13)所示的油封与润滑油界面上的热流连续性条件、式(14)所示的润滑油与轴界面上的相应连续性条件和式(15)所示的轴传热方程获得。

(12)

(13)

(14)

(15)

式中：ζseal为油封线速度，文中假设油封固定，速度为0；ζshaft为轴的线速度；kseal、ρseal、cseal与kshaft、ρshaft、cshaft分别代表油封与轴的导热系数、密度、比热容；Zseal、Zshaft与坐标Z方向相同，Zseal=0位于油封表面，Zshaft=0位于轴表面。

关于Zseal、Zshaft和Z的量纲一化处理方法，可以参考文献[19]。在求解能量方程时，热边界条件如下：油膜与空气交界处温度等于大气温度，油膜与油腔交界处温度等于油腔温度，油腔与空气为定温。油膜与油封表面交界处温度等于油封表面温度，与轴表面交界处温度等于轴表面温度。

因为润滑油的黏度和温度紧密相关，所以用式(16)的黏压-黏温方程计算流体黏度[20]。

μ=μ0·θ·exp{(lnμ0+9.67)[-1+(1+5.1×10-9p)ψ[(T-138)/(T0-138)]-s0]}

(16)

(17)

式中：ψ、s0分别由式(18)、式(19)计算；θ为密度比；ρ1为与温度、压力相关的流体密度，由式(20)计算。

(18)

(19)

(20)

式中：α、β分别为黏压、黏温系数；T0为初始温度。

2.5 泵吸率与摩擦扭矩计算

泵吸率是描述油封密封性能的一项重要参数。泵吸率过小时，会因为密封腔体内侧压力小于外压，润滑油会因此泄漏。合适的泵吸率是判断油封性能是否合格的关键。式(21)为油封泵吸率的表达式。

(21)

式中：μ为流体黏度。

将量纲一化参数引入式(21)，进行归一化后得泵吸率Q，如式(22)所示。

(22)

泵吸率Q为负值时说明油封密封空间内的润滑油会发生泄漏；泵吸率为正值时，说明密封腔体内润滑油被反向泵吸回油侧。

摩擦扭矩是研究油封密封性能的另一项重要指标。文中的摩擦扭矩由式(23)计算。

(23)

式中：ff为总摩擦力，是干摩擦力矩和黏性摩擦力矩的总和，由式(24)计算。

ff=-∬τx|z=hdxdy

(24)

τx|z=h为密封唇口表面周向剪切力，由下式给出：

(25)

参数φf、φfp、φfs分别由式(26)—(28)计算。

当H≤3时，

z(60+147z)))))]}

(26)

当H>3时，

(27)

式中：z=H/3。

φfp=1-1.4e-0.66H

(28)

φfs=11.1H2.31e-2.38H+0.11H2

(29)

干摩擦力主要是由粗糙峰接触而产生，由粗糙峰接触压力pc与固体摩擦因数kasp乘积所得，固体摩擦因数kasp取0.2[20]。因此：

(30)

3 油封的数值计算结果分析

3.1 数值计算流程

为顺利建立油封唇口温度分布的数值模型，针对稳定运行油封唇口温度的模拟计算，对油封模型进行以下假设：

(1)假设润滑油满足黏性内摩擦定律，为牛顿流体；

(2)润滑油、旋转轴、油封橡胶的导热系数、比热容均为常数；

(3)在油封开始工作瞬间，油封接触区域的温度一定，且受力均匀；

(4)假设油封材料特性不随温度的升高而变化。

数值计算流程如图8所示。

图8 数值计算流程Fig.8 Numerical calculation flow

3.2 油封有限元分析结果

图9所示为通过有限元分析软件Abaqus仿真分析得到的不同织构油封的静态接触压力分布。可以看出，油封与旋转轴轴向接触宽度Ly=0.290 0 mm，最大接触压力位于唇尖处为6.046 8 MPa。由于微织构为凹坑式设计，因此织构处的静态接触压力小于唇尖其他部位。

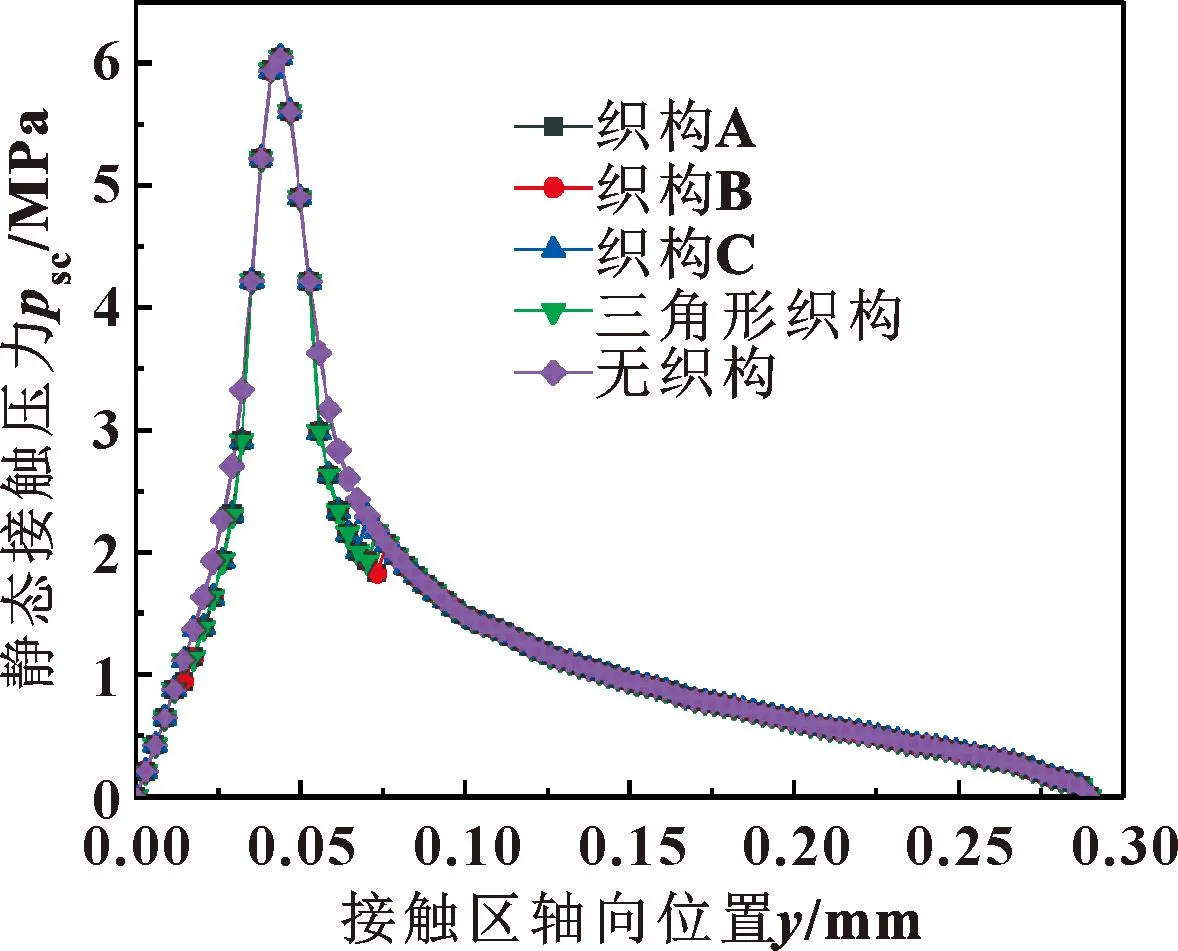
图9 不同织构油封静态接触压力分布Fig.9 Static contact pressure distribution of oil seals with different textures

图10所示为不考虑微织构油封的径向变形影响系数矩阵。以上矩阵是在Abaqus软件中将单周期内区域划分成100×100个节点，在油封唇口节点处依次施加单位节点力后，分析所有节点变形情况所得到的。

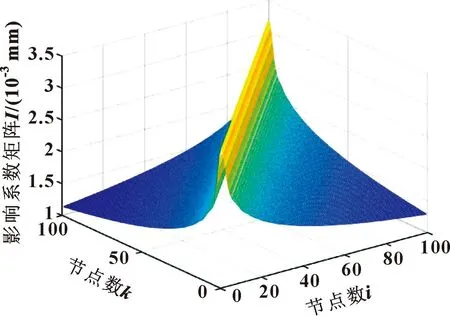
图10 无织构时油封的径向变形影响系数矩阵Fig.10 Radial deformation influence coefficient matrix of oil seal without texture

3.3 油封的数值模型验证

为验证数值模型正确性，采用与文献[21]相同模型数据和实验数据对文中模型进行了验证。文献[21]选用90 mm×118 mm×10 mm氟橡胶油封，试验轴转速为1 000 r/min，油封过盈量为0.65 mm，油温为73 ℃。文中模型计算的唇口最高温度和文献试验结果如表3所示。两者结果对比误差小于1%，故验证了文中模型可靠性。

表3 油封唇口最高温度计算值和文献值比较

3.4 油封的数值计算结果及分析

图11所示为轴转速为1 000 r/min，油腔温度为70 ℃，粗糙度为1 μm时油封唇口接触宽度上油膜温度分布。

图11 不同织构油封唇口温度分布Fig.11 Temperature distribution of oil seals with different textures

可见，无论织构油封还是非织构油封唇口温度最高值位于唇尖位置，这是由于唇尖处的接触压力最大，产生的摩擦力也最大，摩擦产生的热量就越多，温度最高。从唇尖到接触区两侧温度逐渐降低。3种表面织构由于其面积相近，而形状的不同对最高温度的数值影响非常微小，各种织构油封油膜温度分布几乎一样，无织构油封油膜温度较织构油封在唇尖处温度略高，无织构油封油膜热量在唇尖处更加集中。

图12所示为最高温度随旋转轴转速变化情况。最高温度都随转速增加近似线性递增。随着转速的增加，摩擦产生的热量也会增加，虽然转速增加也会引起唇口处流体流动性增强，换热能力增加，但摩擦产生的热量大于散失的热，最终使得最终唇口最高温度逐渐升高。

图12 不同织构油封唇口最高温度随转速的变化Fig.12 Variation of maximum lip temperature of oil seals with different textures with rotation speed

图13所示为泵吸率随温度变化曲线。显然，油封泵吸率随油封唇口温度升高而下降，润滑油从空气侧向油侧回流能力减弱。当温度升高到一定值，如织构油封在340 K，油封泵吸率会下降到零以下，增加了泄漏风险。在不同温度下织构油封较无织构油封对泵吸率都有明显提升作用，其中以织构A对油封泵吸率的影响效果最佳。

图13 不同织构油封泵吸率随温度的变化Fig.13 Variation of pump suction rate of oil seals with different textures with temperature

图14所示为摩擦扭矩随温度的变化曲线。显然，在转速相同情况下，随着温度的升高摩擦扭矩减小，这是由于油液黏度随温度升高而降低导致黏滞摩擦力减小。相同温度下，无织构油封所产生的摩擦扭矩大于织构油封，因为织构的存在使油膜厚度增大，减少了粗糙峰接触摩擦力。 油液黏度在低温时对温度变化更敏感，温度升高也会导致油膜厚度变小，粗糙峰接触引起的摩擦力也会增加，因此，随着温度的升高摩擦扭矩的下降趋势也逐渐放缓。

图14 不同织构油封摩擦扭矩随温度的变化Fig.14 Variation of friction torque of oil seals with different textures with temperature

图15所示为最小油膜厚度随温度的变化情况。可见，随着温度升高油封唇口最小油膜厚度持续下降。若唇口温度继续升高，油膜厚度会持续下降，直到不能保持油膜的完整性，导致唇口与轴间的接触区域的干摩擦过大，使得油封唇口磨损、唇口材料老化变形，进而使润滑失效。

图15 不同织构油封油膜厚度随温度的变化Fig.15 Variation of oil film thickness of oil seals with different textures with temperature

图16所示为轴转速为1 000 r/min，油腔温度为70 ℃时，油膜厚度轴向分布。可见，与无织构油封相比，织构油封除在织构处存在润滑油集聚因而油膜厚度较高外，其余部分油膜厚度无明显差别。因此在求平均油膜厚度时，织构油封所产生的平均油膜厚度值更大一些。

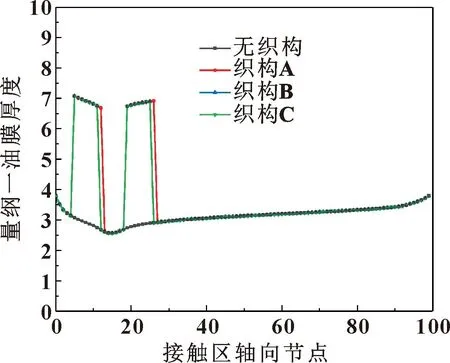
图16 不同织构油封油膜厚度的轴向分布(1 000 r/min，70 ℃)Fig.16 Axial distribution of oil film thickness of oil seals with different textures(1 000 r/min，70 ℃)

4 结论

(1)油封工作时，最高温度位于唇尖处，接触区温度从油封唇尖至两侧温度值逐渐降低，无织构油封最高温度略高于织构油封，无织构油封在唇尖处热量会更集中。随着旋转轴转速增加，摩擦产生的热量也逐渐增加，油封唇口最高温度几乎呈线性递增，由于织构的存在会导致摩擦减小。

(2)织构油封对泵吸率的提升效果较为明显，其中以织构A油封效果最为显著。织构也会引起油液的聚集，从而提升平均油膜厚度，增强润滑效果。

(3)随着油液温度升高，会导致润滑油黏度逐渐减小，油封泵吸率、摩擦扭矩以及油膜厚度都会下降，油封密封性能明显降低。当温度升高到一定程度，油封泵吸率会降为负值，存在油液泄漏风险。