基于疫苗接种的SEIHRVI传染病模型分析与最优控制

薛亚奎, 任亚鑫

(1. 中北大学 数学学院, 山西 太原 030051;2. 齐鲁理工学院 计算机与信息工程学院, 山东 济南 250200)

传染病对公众健康和经济发展威胁巨大。对传染病模型的研究能够捕捉到传染病显著的传播模式,且具有数学上的可处理性,为理解传染病的定性行为提供必要的见解,并为控制政策提供指导。

许多学者在疫苗接种方面进行了研究[1-6],但这些模型只是简单地用一个参数代表易感者接种后变为恢复者的转化率,并非将接种者单独作为一类,且认为疫苗完全有效,可提供永久免疫。目前一些国家的研究清楚的表明,疫苗并不总是能提供完全的免疫力。由于疫苗提供的免疫力弱或丧失,一段时间后部分接种者可能会感染。针对这一情形,Yang等[7]增加了接种疫苗类,提出SVAIR模型,结果表明其对提高疫苗接种率有效,但若仅靠提高接种率并不能很快实现控制。Buonomo等[8]具体考虑了接种疫苗不是强制性的情形,个体根据疾病传播的当前和过去信息作出接种决定,讨论了SEVIR模型。Turkyilmazoglu[9]基于双线性发生率对传统的SIR模型进行改进,主要研究疫苗不能提供完全的免疫所产生的影响。但事实上传染病并不是在封闭的环境内传播,另外单位时间内感染者接触的人数会受到限制,或者随着总人口规模的增加,其增长速度应降低[10]。因此,Gu等[11]和蒋贵荣等[12]均采用标准发生率研究传染病模型。在文献[9]的基础上,本文考虑疫苗接种的影响,提出带有标准发生率的传染病模型,并对系统进行优化控制分析。

1 模型建立

将总人口N分为易感者S、潜伏者E、感染者I、住院者H、接种者V和恢复者R六类。假设:①只有易感者接种疫苗;②处于潜伏期的个体尚不能将病毒传播给他人[8,11,13];③考虑到疫苗不能提供永久免疫,因此接种者仍存在被感染的风险。基于以上假设,建立具有疫苗接种的扩展模型如下:

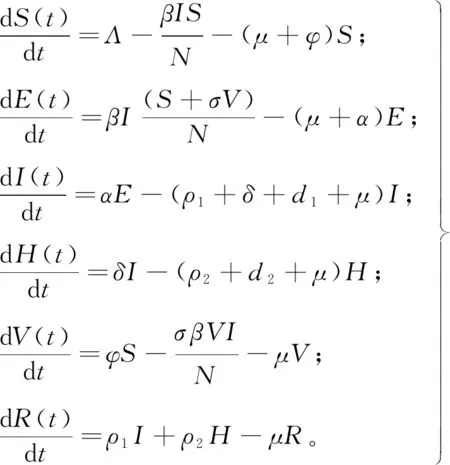
(1)

式中:Λ为人口的常数输入率;β为易感者接触感染者后的感染率;σ为疫苗无效率;φ为疫苗接种率,ρ1、ρ2分别为I和H的恢复率;d1、d2分别是I和H的因病死亡率;α为E向I的转化率;δ为I的住院率;μ为自然死亡率。

命题1 令S(0)、E(0)、I(0)、H(0)、V(0)、R(0)为模型(1)的非负初始条件,则对∀t≥0,模型(1)的解都是非负的。

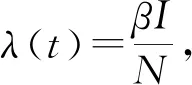
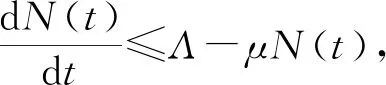
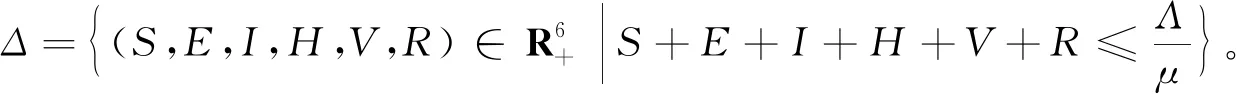
(2)

2 平衡点和基本再生数

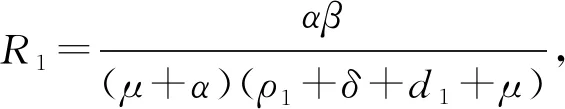
定理1 当R0>1时,模型(1)在Δ内存在唯一的地方病平衡点E1=(S*,E*,I*,H*,V*,R*)。

证明 令模型(1)式子右端等于0,

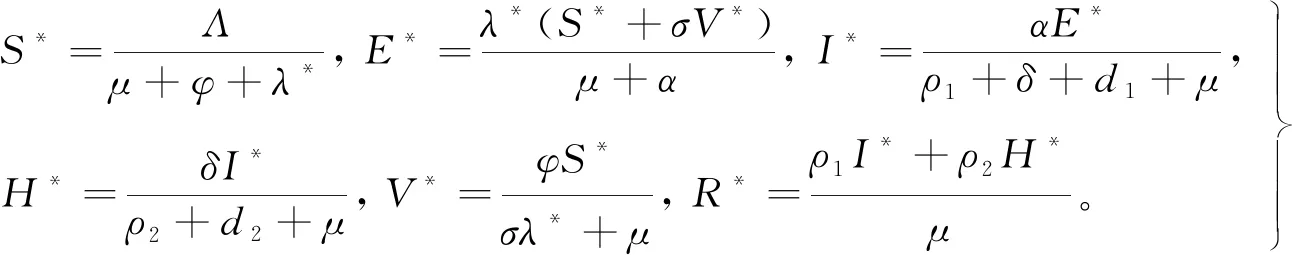
(3)

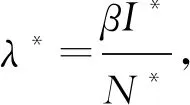
a0λ*2+a1λ*+a2=0,

(4)

式中:

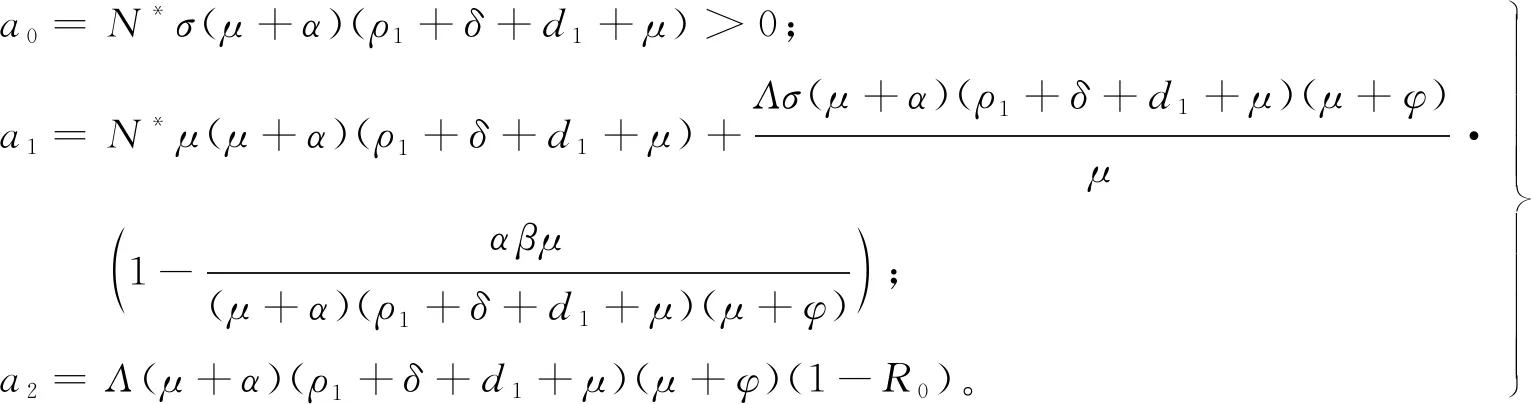
(5)

当R0>1时,a2<0,可知式(4)的两根为一正一负。因此当R0>1时,存在唯一的正平衡点E1。

3 平衡点的稳定性

定理2 当R0<1时,模型(1)的无病平衡点E0在Δ上局部渐近稳定。

证明 模型(1)在E0处的Jacobian矩阵为

显然,J(E0)的特征值有-(μ+φ),-(ρ2+d2+μ),-μ(二重)。其余特征值为以下多项式的根

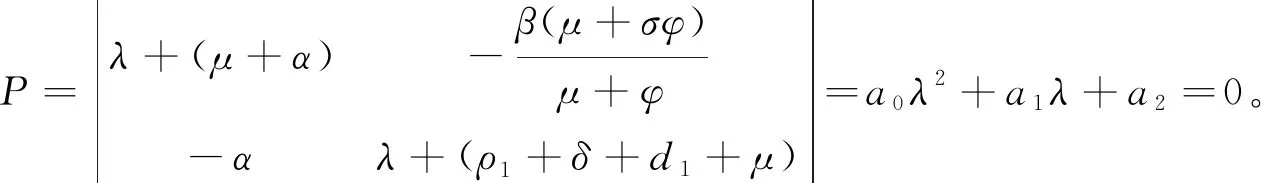
(6)

式中:

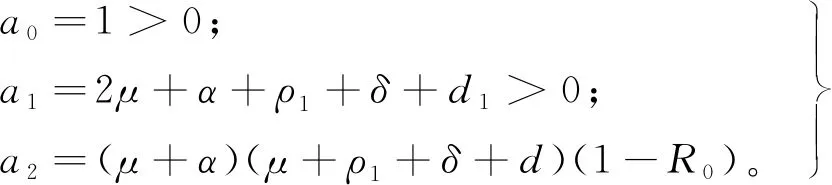
(7)

当R0<1时,a2>0,根据Hurwitz判据,矩阵J(E0)的特征值均有负实部,即定理2得证。

定理3 当R0<1时,模型(1)的无病平衡点E0在Δ上全局渐近稳定。

证明 考虑Lyapunov函数

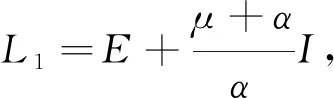
(8)

计算L1沿模型(1)的导数,有

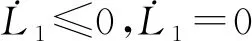
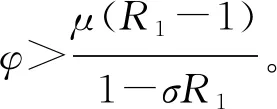
定理4 当R0>1时,模型(1)的地方病平衡点E1在Δ上全局渐近稳定。

证明 为研究平衡点的稳定性,考虑模型(1)的极限系统[16],由于R与其他项独立,简化为如下模型:

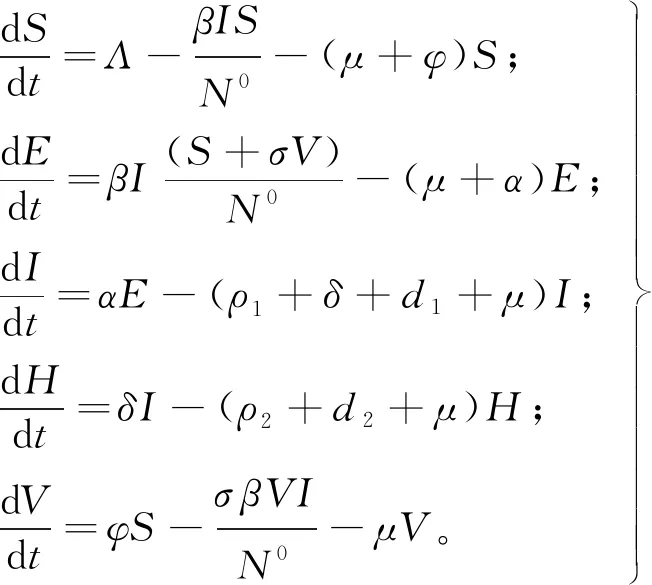
(10)

构造Lyapunov函数

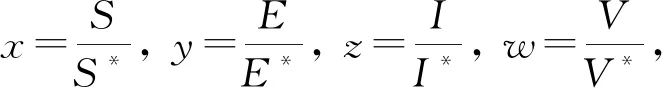
根据文献[17]中的代数方法,利用均差不等式的性质,定义函数

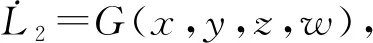
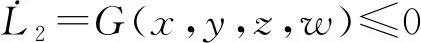
4 最优化控制

为有效预防控制传染病的传播,研究对疾病施加限制并保持成本最小的最优控制策略。引入控制变量ui(t)(i=1,2,3):u1(t)代表个人防护措施(保持卫生、注意社交距离、媒体宣传);u2(t)代表接种疫苗率;u3(t)代表住院者的恢复率。建立如下最优控制模型:

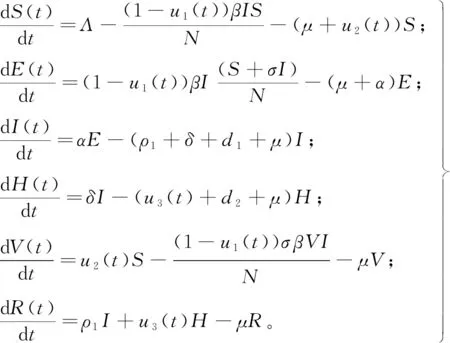
(14)

设目标函数为

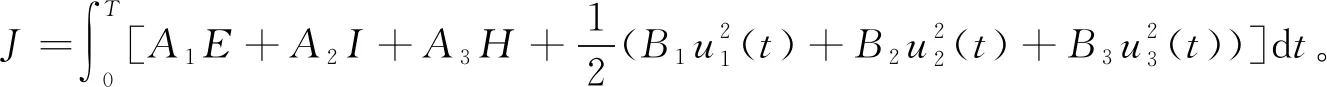
(15)

式中:T为末态时间;A1、A2、A3分别是E、I、H的权重系数;B1、B2、B3分别是控制变量u1、u2、u3的正权重系数。寻找最优控制,使得

(16)

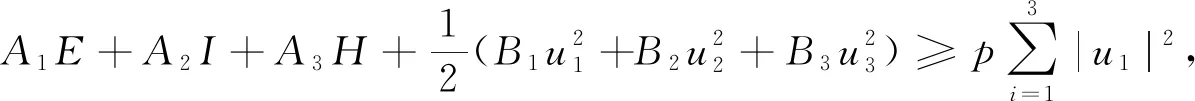
为寻找最优控制解,定义哈密顿函数

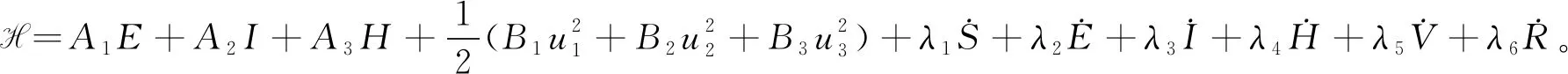
(17)

式中λi(t),i=1,2,3,4,5,6是各状态的伴随变量。

(18)

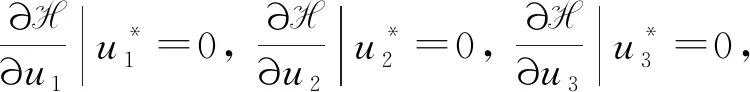
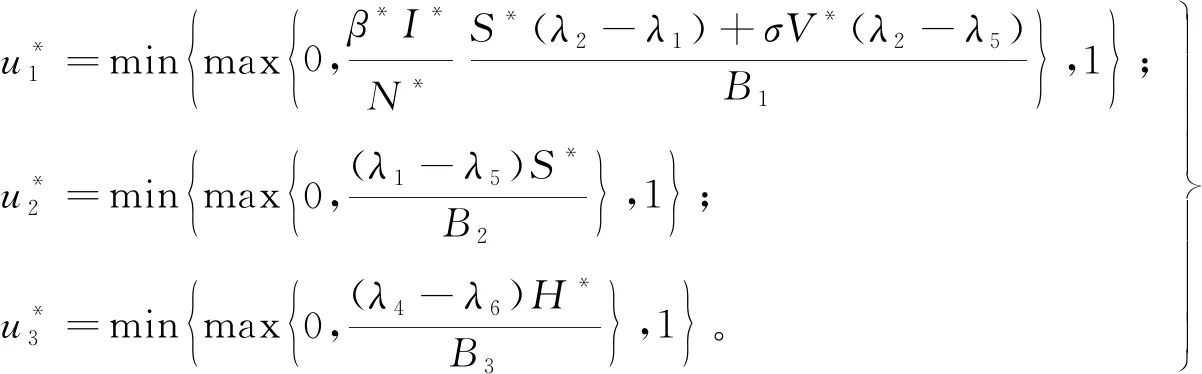
(19)

5 数值模拟

通过数值模拟对理论分析的结果进行检验,部分数据源于文献[7-8]中。图1(见封3)为各类人数的时间序列,其中小图是对应大图的细节放大图,以便清晰地观察各曲线的变化状态。图1(a)模拟了无病平衡点E0的稳定性,参数取值为Λ=1 762,μ=0.000 107,β=0.688 3,φ=0.014 3,ρ1=0.055,ρ2=0.165,α=0.557,δ=0.12,σ=0.2,d1=0.000 624 8,d2=0.000 238 56,此时,R0=0.806 5<1,E、I、H的数量趋近于0,代表疾病灭绝。图1(b)模拟了地方病平衡点E*的稳定性。参数选取为Λ=1 762,μ=0.033,β=0.888 3,φ=0.02,δ=0.12,ρ1=0.055,ρ2=0.165,α=0.557,d1=0.000 624 8,d2=0.000 238 56,σ=0.2,此时,R0=2.806 2>1。在图1(b)的细节图中可以看出,各个变量的曲线变为一条直线,意味着疾病一直持续。

接下来,对几个关键参数进行灵敏度分析,旨在确定有助于减少疾病传播的参数,进而采取相关措施。图2和图3所示曲线为基本再生数R0的等值线,由图可以看出,R0随φ与δ的增大而降低,随σ与α的增大而增大,且相较之下,σ和δ所产生的影响更大。因此,应着重注意提高疫苗的效力和住院率。

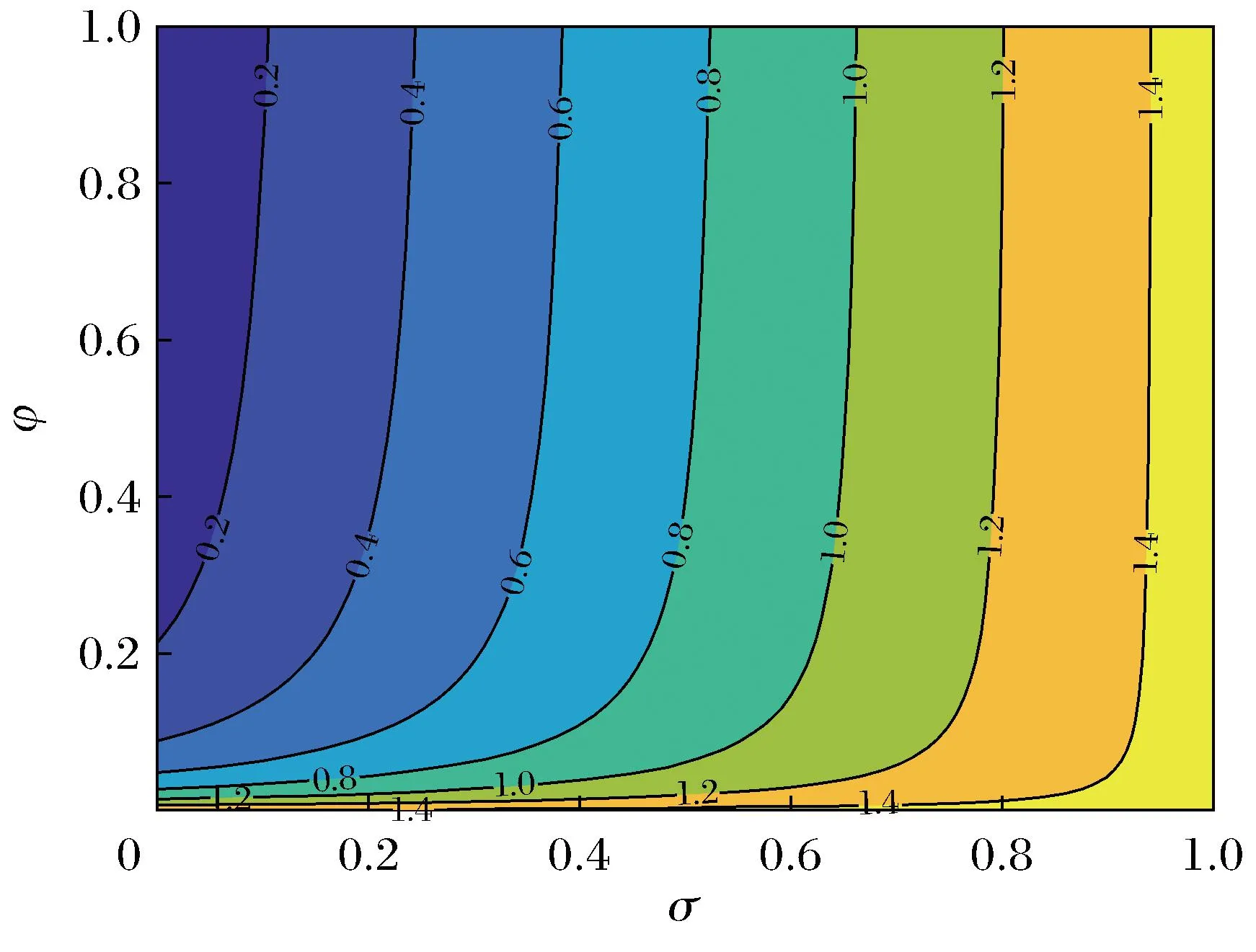
图2 φ和σ对R0的影响

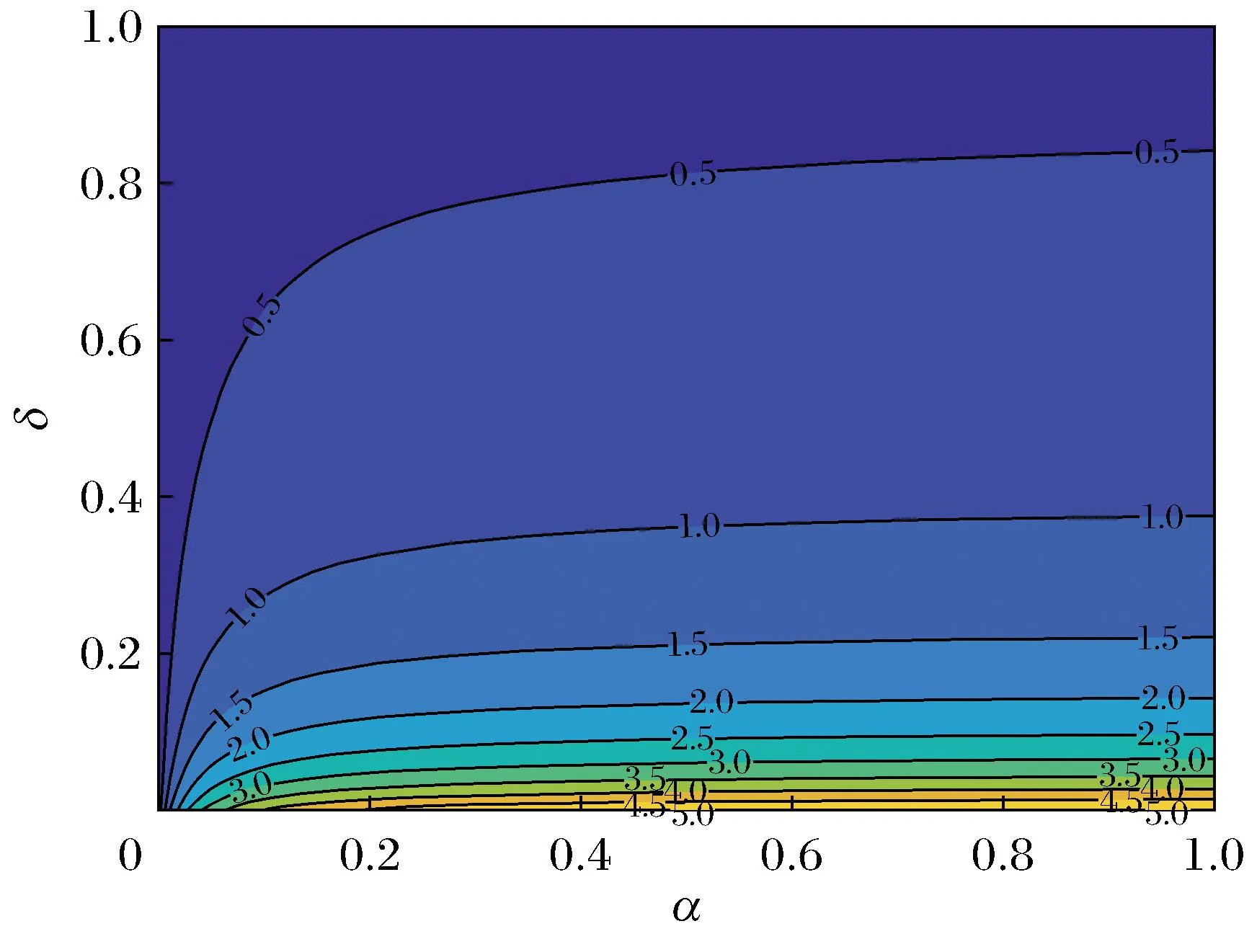
图3 δ和α对R0的影响

在模拟控制策略对传染病传播的影响中,取定初值为S(0)=5×107,E(0)=1 000,I(0)=500,H(0)=50,V(0)=100。图4(a)～图4(e)分别比较了有无控制的S、E、I、H、V的人数变化,其中图4(b)～图4(d)分别具有前100天E、I、H的人数变化的放大图,在放大图中可以清楚的看到实施控制措施时E、I、H的人数的变化趋势。图4表明,在采取最优控制策略后,S、E、I、H的人数明显减少,V的人数显著增加。因此,该最优控制策略对于控制疾病传播有效,不仅控制了染病者数量,而且使接种者人数保持在较高的水平。

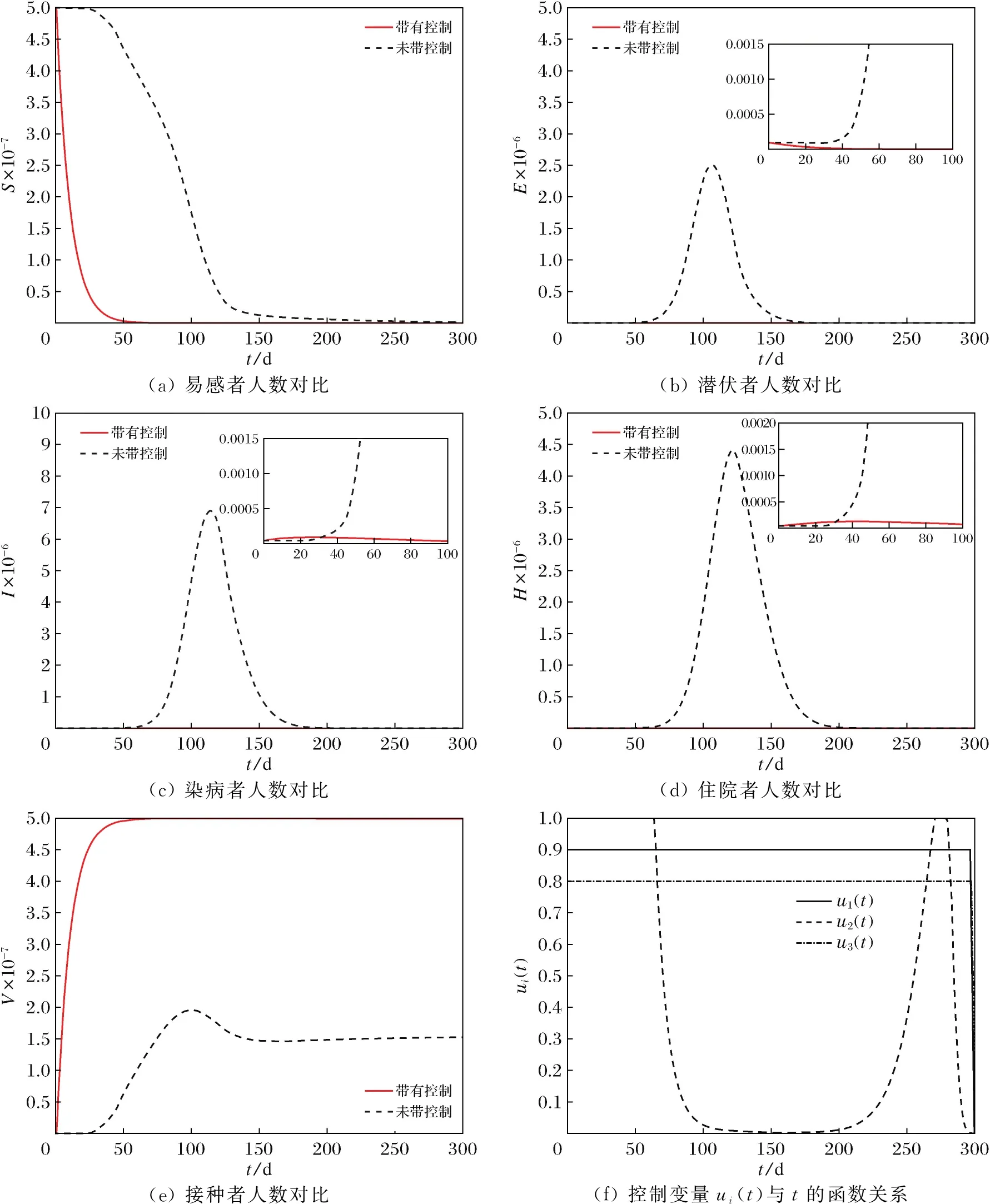
图4 最优控制模拟

考虑到医疗技术和成本的限制,设置控制变量的边界分别为u1=[0,0.9],u2=[0,1],u3=[0,0.8],得到最优控制策略如图4(f)所示。值得注意的是接种策略u2随时间的变化,在下降到趋于0后又逐渐增长到1。

6 结 论

考虑到疫苗不能提供永久的免疫力,一段时间后接种者可能会再次感染,建立了具有疫苗接种影响的传染病动力学模型。相比文献[9],本文采用标准发生率并拓展了隔间类型,展现了模型的普适性。借助构造Lyapunov函数证明了:当R0<1时,无病平衡点全局渐近稳定;当R0>1时,存在唯一的地方病平衡点且其全局渐近稳定。对控制策略进行模拟后的结果表明:注意自我保护、扩大接种疫苗范围以及重视治疗可有效控制传染病的传播。鉴于疫苗的不完善性,接种后也应注意个人防护,避免感染。