肺部免疫应答模型的稳定性分析与分支分析
代梦雅, 张存华, 刘金龙
(1.兰州交通大学 数学系, 甘肃 兰州 730070;2.丁门村小学, 甘肃 天水 741315)
0 引言
肺炎一般指肺部包括肺泡、远端的气管、肺间质的感染性炎症.肺炎可以由疾病、微生物、理化因素、免疫损伤、过敏及药物所致.目前,细菌性肺炎是最常见的肺炎,也是最常见的感染性疾病之一.通常有高热、咳嗽、咳痰等症状.但对于像婴儿和老年人这样身体抵抗力低下的重症患者,在治疗疾病的过程中可能需要呼吸机,这样就大大地增加了感染呼吸机相关性肺炎的概率.呼吸机相关性肺炎主要是和使用呼吸机有密切联系的肺炎,具体是指使用呼吸机治疗48小时之后,到拔管48小时内出现的肺部感染性炎症,文献[1]表明它是重症患者中第二大医院获得性疾病.文献[2]表明它的死亡率很高,病情发展很快,容易漏诊、误诊.因此早诊断早治疗非常重要.肺部的保护系统主要是先天免疫系统和适应性免疫系统,当巨噬细胞无法吞噬病原体时,可以发出信号招募其他免疫系统的组成成分,文献[3-5]表示中性粒细胞比巨噬细胞更有效.
当病原体入侵数量增加时,先天免疫系统的细胞数量会随之增加来保护肺部.基于现有的肺部免疫系统的有关生物学知识, Young等[6]构建了以下模型:
(1)

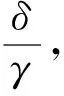
(2)
下对系统的动力学行为进行了研究.但是对于不同种类的病原体会有一定的差异,较大的病原体负荷可能无法克服先天免疫系统.所以Shi等[7]在条件
(3)
下对系统的动力学行为进行了研究.
文献[8]考虑到当病原体入侵数量增加时,先天免疫系统的细胞的数量可能会迅速扩大规模来保护肺部,将模型(1)修改为:
(4)
并在条件(3)下证明了模型(4)边界平衡点是全局渐近稳定的.
文献[8]通过变量代换
并用x,t,z代替x1,t1,z1,将模型(4)化为
(5)
其中
由式(3)知p3<1,且p1,p2,p3,p4,p5都是正的.所以我们在下面的条件下研究模型(5)
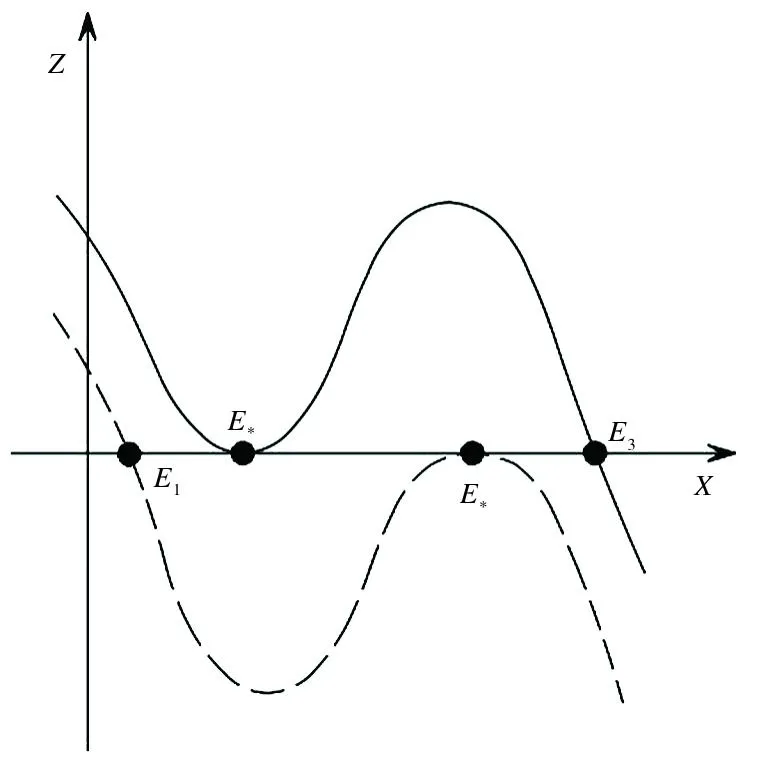
0 (6) 易知Ω={(x,z)|x≥0,z≥0}是模型(5)的正不变区域. 为了讨论模型(5)存在正平衡点的条件,考虑以下方程: (7) 从而有 (8) 令 f(x)=ax3+bx2+cx+e, (9) 则 f′(x)=3ax2+2bx+c, (10) 其中 a=p2(p3-1),b=p2(p5-p4)-p1p3, c=p3-1-p1p5,e=p5-p4. 由条件(6)我们得到a<0,c<0. 下面将在满足条件(6)下考虑模型(5)正平衡点的稳定性.模型(5)在E(x,y)处的雅可比矩阵是 则J(E)的行列式是 (11) J(E)的迹是 (12) 由模型(5)中f(x)=0得 (13) 把式(13)代入式(10)和式(11)得 (14) 和 (p3-1)(p2x2+1). (15) 由式(14)和式(15)可以推出 (16) 所以,若f′(x)≠0,则E(x,z)是初等平衡点. 特别地,当f′(x)>0时,对应的平衡点是双曲鞍点,当f′(x)=0时,对应的平衡点是退化平衡点. 这一节我们考虑模型(5)在满足条件(3)下有正平衡点的条件,以及在该条件下,模型(5)正平衡点的类型和稳定性. 根据三次多项式方程根的判别式可得 其中 a=p2(p3-1), b=p2(p5-p4)-p1p3, c=p3-1-p1p5. 首先讨论当b>0时,其中b=p2(p5-p4)-p1p3,由于e=p5-p4,所以当b>0时,e>0,再由上述讨论可得以下引理. (Ⅰ) 若Δ>0,则模型(5)存在一个正平衡点E1(x1,z1)或E3(x3,z3),E1或E3是一个初等平衡点; (Ⅱ) 若Δ=0,则模型(5)存在两个正平衡点,一个是退化的平衡点 另一个是初等平衡点E1(x1,z1)或E3(x3,z3); (Ⅲ) 若Δ<0,则模型(5)存在三个不等的正平衡点E1(x1,z1),E2(x2,z2)和E3(x3,z3),其中E1和E3是初等平衡点,E2是一个双曲鞍点. 证明由式(16)和图1-3得, Det(J(E1))>0,Det(J(E*))=0,Det(J(E3))>0,Det(J(E2))<0, 这隐含着E1和E3是初等平衡点,E*是一个退化的平衡点,E2是一个双曲鞍点.证毕. 图1 存在一个正平衡点E1或 E3 图2 存在两个正平衡点E*和E1或E3 图3 存在三个不等的正平衡点E1,E2和E3 下面我们讨论平衡点的详细类型及稳定性. 先讨论平衡点E1的详细类型及其稳定性. 由式(12)得 (17) 又由Tr(J(E1))=0可得 由上述讨论我们可以得到以下定理. E3的讨论与E1方法相同,这里不再赘述. 下面讨论E*的具体类型及其稳定性. 由引理1可知Det(J(E*))=0.由Tr(J(E*))=0可得 所以可得以下定理. 定理2假设引理1中(Ⅱ)成立,那么有: (ⅰ) 若A1,A2≠0,则E*是一个余维2的尖点; (ⅱ) 若A1≠0,A2=0,则E*是一个余维至少3的尖点. 证明当引理1中(II)成立时,我们可以得到 因此我们首先令X=x-x*,Z=z-z*,则模型(5)转化为 (18) 其中 再令 仍用t代替τ,则模型(18)转化为 (19) 其中 由文献[9]的中心流形方法,我们可以得到限制在中心流形上的方程 (20) 经计算得a13+a21-p3a11≠0,因此b11≠0. 仍用t代替τ,则模型(18)转化为 (21) 其中 由文献[10]第二章相关引理可得 (22) (23) 在原点的小邻域里模型(22)经过非奇异的变换与模型(23)是等价的. 所以用x,z代替u,v,模型(21)转化为 (24) 其中A1=d21,A2=d22+2d11. 所以若A1,A2≠0,则E2是一个余维2的尖点;若A1≠0,A2=0,则E2是一个余维至少3的尖点. 其次讨论当b<0时,其中b=p2(p5-p4)-p1p3,由于e=p5-p4,所以当b<0时,根据e的正负以及上述讨论可得以下引理. (Ⅰ) 若e>0,则模型(5)存在一个正平衡点E4(x4,z4),且E4是一个初等平衡点; (Ⅱ) 若e≤0,则模型(5)不存在正平衡点. 证明由模型(24)和图4、图5得,Det(J(E1))>0,这隐含着E4是初等平衡点. E4的稳定性讨论同E1(见上述定理1),在这里不再赘述. 最后讨论当b=0时,其中b=p2(p5-p4)-p1p3,此时存在虚根,不做详细讨论. 图4 存在一个正平衡点E4 图5 不存在正平衡点 这一节讨论分支. 由定理1和定理2我们知道曲面 是鞍结点分支曲面.其中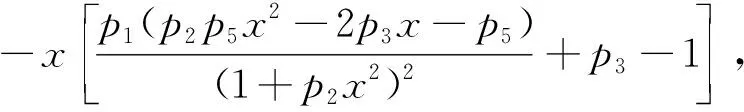
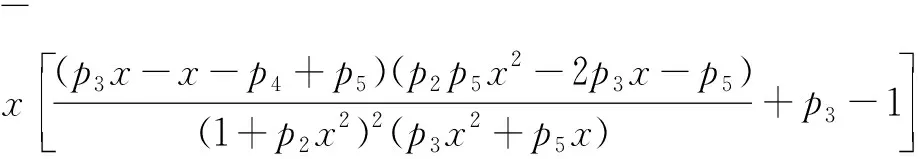
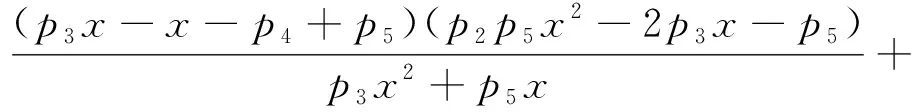
1 正平衡点的类型和稳定性


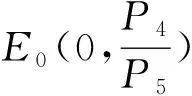
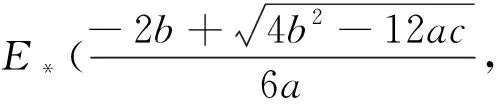
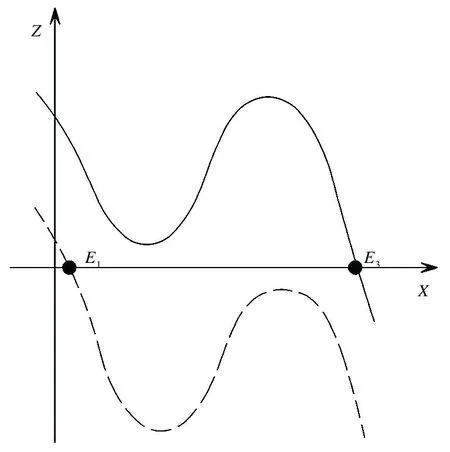

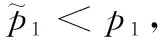


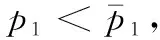
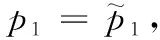
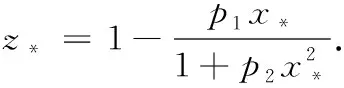
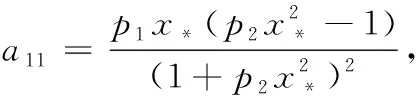

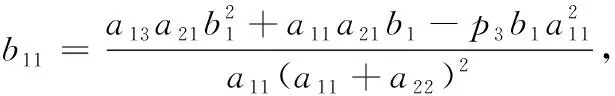
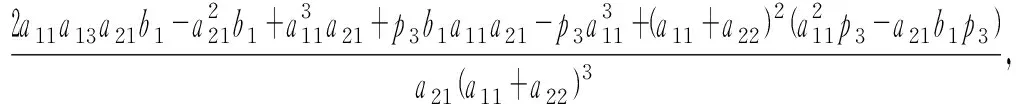
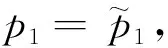
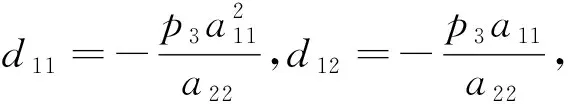
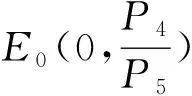


2 鞍结点分支