小q-Schur代数uk(3,3)的中心
杨 倩, 刘明强
(三峡大学 三峡数学研究中心, 湖北 宜昌 443002)
0 引言
q-Schur代数是由Dipper等[1-2]在Schur代数的基础上定义的,在有限一般线性群的表示方面被广泛研究. Beilinson等[3]利用q-Schur代数给出了量子群的几何实现,指出量子群到q-Schur代数之间存在一个代数满同态. 小q-Schur代数与q-Schur代数的关系类似于A型的无穷小量子群与量子群的关系.于是,Du等[4]和Fu[5]利用无穷小量子gln引入了小q-Schur代数uk(n,r),并指出小q-Schur代数uk(n,r)是域k上q-Schur代数的子代数. 进而Fu[6]探究了无穷小q-Schur代数结构和小q-Schur代数之间的关系,将小q-Schur代数uk(n,r)的定义推广到任意次单位根的情况,并构建了小q-Schur代数不同类型的基[5]. Du等[7]还对小q-Schur代数的表示进行研究,对q-Schur代数的单模和半单的小q-Schur代数进行分类,给出了小q-Schur代数在奇次单位根下有限表示型的分类.
代数的中心在研究代数的结构和性质时发挥重要作用.文献[8-10]广泛研究了量子群的中心. Geetha等[11]利用对称群中的共轭类描述了Schur代数中心的一组基元,主要根据Schur最初使用的基给出这些基元的组合描述. 在量子群和量子包络代数的中心已比较清楚之后, Gao等[12]利用q-Schur代数U(2,r)的正规化基[A]A∈Ξ(2,r)给出了q-Schur代数U(2,r)中心的一组基元,但只考虑了q-Schur代数的一种特殊情况. Fu[13]通过Hecke代数的中心构造了(v)上q-Schur代数中心的基. 对于小q-Schur代数中心的研究较少,当n=2时,对任意l次单位根,当r v是一个参数,设A=[v,v-1].k是一个含奇数l次本原单位根ε的域. 当v特殊化为ε, 可把k看作A-模.设是上所有非对角元素属于的n×n矩阵构成的集合.记Ξ(n)=Mn()是在上的子集,映射σ:Ξ(n)→是把任意一个矩阵映射到该矩阵的所有元素之和.设Ei,j=(as,t)是满足as,t=δi,sδj,t的矩阵,其中1≤i,j≤n.对于任意一个r∈,其逆像Ξ(n,r):=σ-1(r)是Ξ(n)的子集并满足对任意矩阵的所有元素求和是r.对于任意的矩阵A=(ai,j)∈Ξ(n,r),其行和序列与列和序列分别为 对于任意的整数N,t(t≥0),设 定理1[3]对于1≤h≤n,R≥0,设A=(ai,j)∈Ξ(n,r), (1)B=(bi,j)满足B-REh,h+1为对角矩阵且co(B)=ro(A),那么有: 其中T={t=(t1,…,tn)|满足t1+…+tn=R,且对于所有的u有0≤tu≤ah+1,u}, (2)C=(ci,j)满足C-REh+1,h为对角矩阵且co(C)=ro(A),那么有: 其中T={t=(t1,…,tn)|满足t1+…+tn=R,且对于所有的u有0≤tu≤ah,u}, 引理1[3]如果λ∈n且D=diag(λ)∈Ξ(n,r),则有 对于正整数l′,设l′=/l′,令映n→(l′)n满足其中j=(j1,j2,…,jn)∈n.令Ξ(n)0是Ξ(n)中对角矩阵构成的集合.q-Schur代数的元素为 设 Λ(n,r)={λ∈n|λ1+λ2+…+λn=r}, 定理2[4]集合 是小q-Schur代数uk(n,r)的一组基. 引理2每个中心元素c∈C(uk(3,3))属于张成集L′,其中 且 为简化符号,设: (1)β3=β4=β5=β6=β7=β8=β1+εβ9=β2+εβ11; (2)β9=β10=β12=β14=β16=β17=β18+εβ13=εβ11+ε2β18; (3)β11=β15,β18=β19. 由定理1和引理1,计算得到 根据等式cei=eic得到对应基元的系数对应相等,将得到的24个等式简化即可得到等式(1)-(3). 将没有化简的等式看作是以β1,…,β19为未知数的齐次线性方程组,设方程组的系数矩阵为M,利用MATLAB将矩阵M简化. 推论1系数矩阵M可以转化为行最简阶梯形矩阵: 设W=(ηi)是以β1,…,β19为未知数的齐次线性方程组的解空间,则dimW=3.取 η1=(1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0)T, η2=(-ε,-1,0,0,0,0,0,0,1,1,ε-1,1,ε-1,1,ε-1,1,1,0,0)T, η3=(0,ε2,0,0,0,0,0,0,0,0,-ε,0,-ε-1,0,-ε,0,0,1,1)T. 定理3当l=3时,小q-Schur代数uk(3,3)中心的维数:dimC(uk(3,3))=3.特别地,集合{c1,c2,c3}是中心C(uk(3,3))的一组基,其中ci=(A1,A2,…,A19)ηi,i=1,2,3. 证明由推论1可知,系数矩阵M的秩为16.集合{η1,η2,η3}是解空间W的一组基础解系,即对于任意的w∈W,有 w=k1η1+k2η2+k3η3=(w1,w2,…,w19)T, 其中k1,k2,k3是常数.那么,对于任意的中心元素,有 即 c=(A1,A2,…,A19)(k1η1+k2η2+k3η3)∈C(uk(3,3)). 记 c1=(A1,A2,…,A19)η1, c2=(A1,A2,…,A19)η2, c3=(A1,A2,…,A19)η3. 于是任意的中心元素都能由c1,c2和c3线性表示. 设l1,l2,l3是常数,记ηi=(ηi,1,ηi,2,…,ηi,19)T,其中i=1,2,3.若 l1c1+l2c2+l3c3=l1(A1,A2,…,A19)η1+l2(A1,A2,…,A19)η2+l3(A1,A2,…,A19)η3=0, 从而有 (l1η1,1+l2η2,1+l3η3,1)A1+…+ (l1η1,19+l2η2,19+l3η3,19)A19=0, 由{A1,…,A19}是基元,得到 l1(η1,1,η1,2,…,η1,19)T+l2(η2,1,η2,2,…,η2,19)T+l3(η3,1,η3,2,…,η3,19)T=l1η1+l2η2+l3η3=0. 又因为集合{η1,η2,η3}是解空间W的一组基础解系,所以得到l1=l2=l3=0.于是集合{c1,c2,c3}是小q-Schur代数uk(3,3)的中心的一组基. 本文研究小q-Schur代数的中心.首先由小q-Schur代数的基元表示出中心元素,再根据中心元素与小q-Schur代数的生成元相乘可交换,得到等式两边对应的项系数相等.从而简化得到所设中心元素的系数需要满足的式子,把所有式子看作以系数β1,…,β19为未知数的齐次线性方程组,于是有系数矩阵M.与文献[14-15]中计算维数的方法不同,我们借助MATLAB软件,得出行最简阶梯形矩阵M′和一组基础解系{η1,η2,η3},从而得到小q-Schur代数的中心C(uk(3,3))的维数和一组基{c1,c2,c3}.1 预备知识
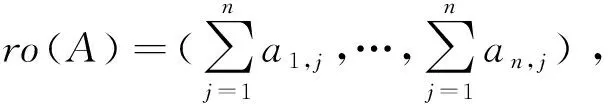


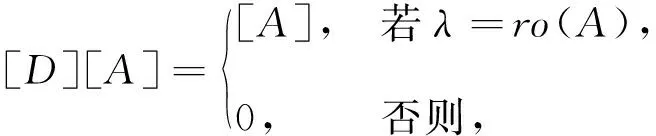
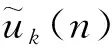
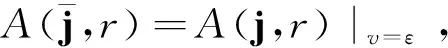
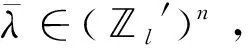
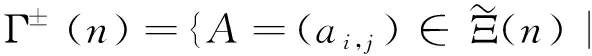
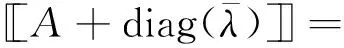
2 主要结论及证明
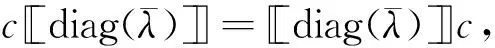
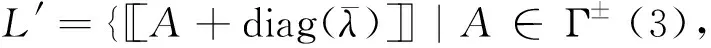


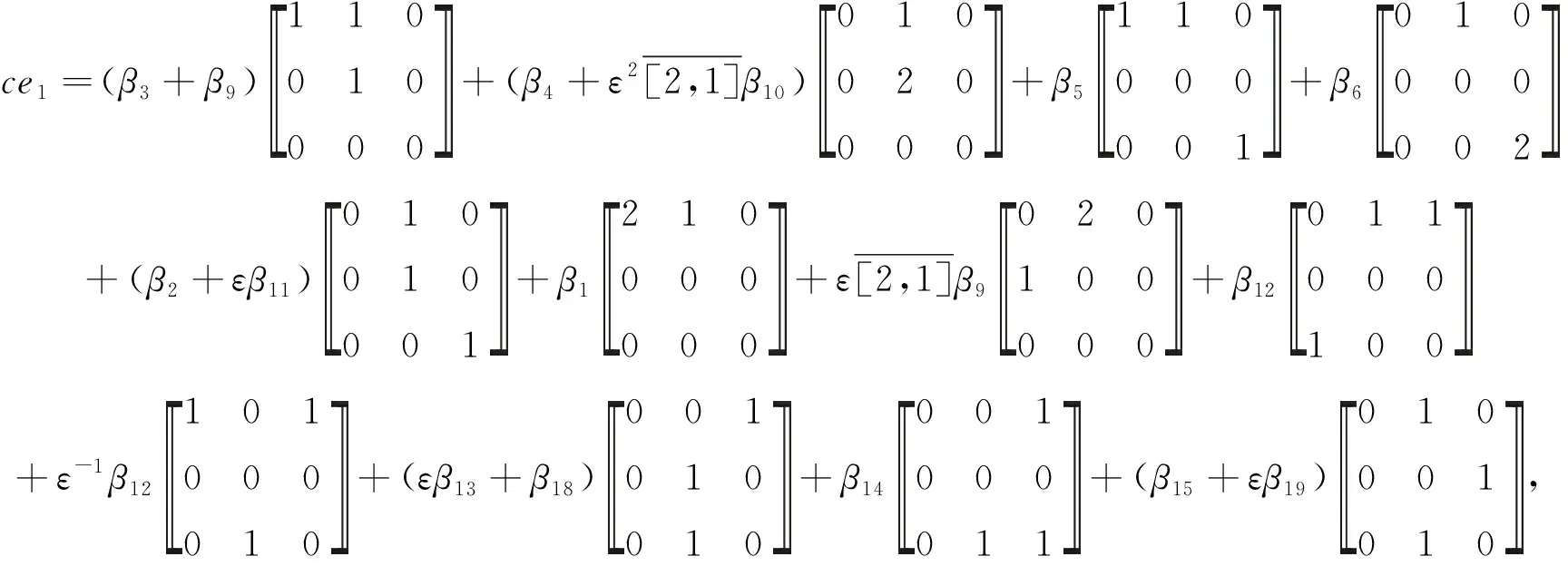
3 总结

