一类二阶迭代泛函微分方程的解析解
夏 梦 莲
(重庆师范大学 数学科学学院, 重庆 401331)
0 引言
迭代泛函微分方程是一种具有复杂偏差变元的新型方程[1].生活中的许多问题都涉及迭代泛函微分方程,如一些人口模型、日用品价格波动模型以及血细胞生产模型等[2].因为这类方程与传统意义下的微分方程有很大的不同,随着未知函数迭代的出现,传统微分方程中经典的存在性定理不能使用,这对该方程的研究造成了很大的困难.虽然近年来,关于迭代泛函微分方程解析解的讨论已有许多结果[1-11],但是依然有必要研究这类方程在一定条件下解析解的存在性.众所周知,n阶时滞微分方程的一般形式为
x(n)(z)=f(z,x(z),x(z-τ1(z)),…,x(z-τk(z))).
在这类方程中,时滞函数τj(z)(j=0,1,…,m)不仅依赖自变量,还依赖未知函数本身,如τj(z)=τj(z,x(z))[3].文献[4]讨论了一类跟状态相关的时滞微分方程
解析解的存在性,本文在文献[4]的基础上,进一步研究迭代泛函微分方程
(1)
在三种情况下的局部可逆解析解,其中,β,γ∈且γ≠0.x[0](z)=z,x[m](z)表示x(z)的第m次迭代(m=1,2,3,4,…).特别的,当β=1,γ=0时,方程(1)为文献[4]所讨论的方程.类似文献[4],为了方便讨论,假设:
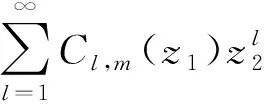
(H2)G(0)=λ∈C{0}.
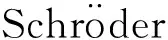
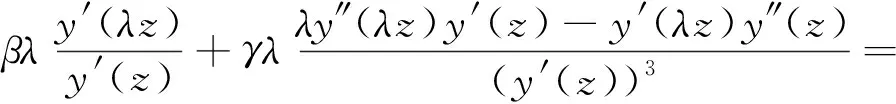
(2)
其中y(0)=0,y′(0)=η≠0.
通过构造方程(2)的收敛的幂级数解,可得到方程(1)具有形如y(λy-1(z))的可逆解析解,本文将分三种情形进行讨论:
(C1)0<|λ|<1,即λ在单位圆内;
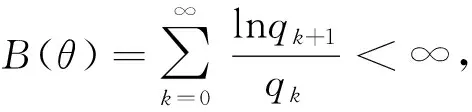

注意到,(C2)是在Brjuno条件下讨论方程(2)解析解的存在性.因此,本文首先给出Brjuno数的相关定义和一些引理.然后讨论三种情况下,辅助方程(2)解析解的存在性,从而得到方程的局部可逆解析解.
1 预备知识
正如文献[13]所提到的,对任意的一个无理数θ,令[θ]表示它的整数部分,{θ}=θ-[θ]表示它的小数部分,于是对任意一个无理数θ有唯一的高斯连分数表示:
简记θ=[d0,d1,…,dn,…],其中{dj}和{θn}通过以下方法得到:
(a)d0=[θ],θ0={θ};
下面我们定义序列(pn)n∈和(qn)n∈:
q-2=1,q-1=0,qn=dnqn-1+qn-2,p-2=0,p-1=1,pn=dnpn-1+pn-2.

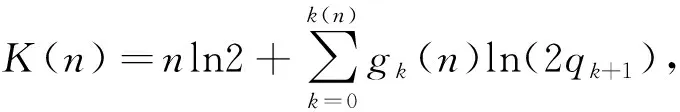
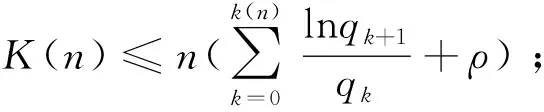
(b)对任意的n1,n2,K(n1)+K(n2)≤K(n1+n2);
(c)-ln|αn-1|≤K(n)-K(n-1).
2 主要结果
定理1假定(C1)或(C2)成立,对∀a1∈C{0}.方程(2)在原点的邻域内有一个形如
(3)
的解析解.
证明设
方程(2)可化为

由于y′(0)=a1=η≠0,故
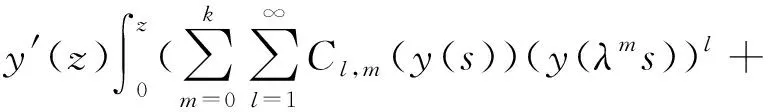
将G(z)、Cl,m(z)、y(z)的展开式代入上式,有
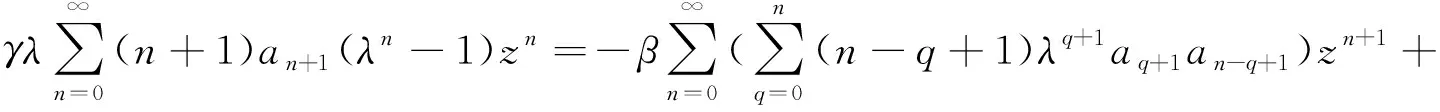
(4)
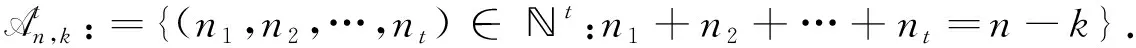
比较式(4)两边同次幂的系数,有
γλa1(λ0-1)=0 ,
(5)
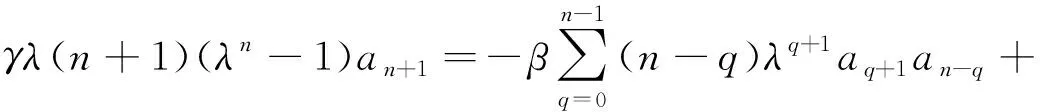
(6)

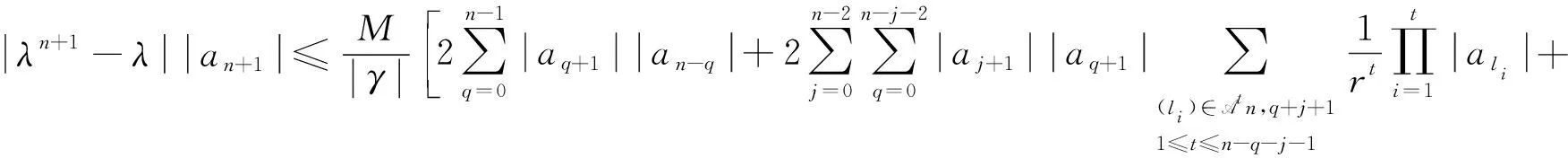
(7)
其中|β|≤M.首先在条件(C1)下,有:

(8)

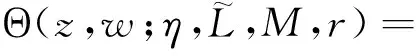
(9)
不难得出:
由隐函数存在定理可知,在原点的邻域内存在唯一的解析函数,使得

(10)
是H(z)收敛的幂级数展开式,将其带入式(8),有
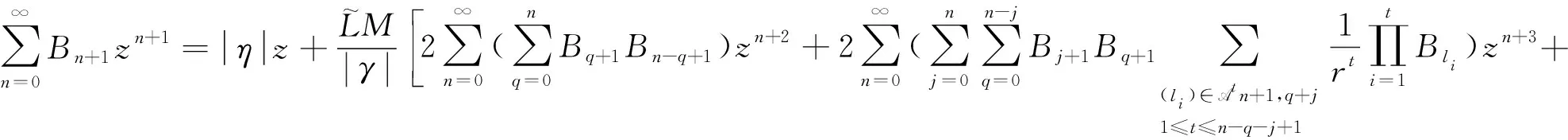
比较两边的系数有:B1=|η|,

(11)
由于|a1|=η=B1,根据式(7)和式(11)可知,对于所有的n≥1,都有|an|≤Bn,故幂级数(3)在原点的邻域内是收敛的.
在条件(C2)下,利用数学归纳法证明|an|≤BneK(n-1),n≥1,其中K:N→R如引理1中定义.显然,|a1|=B1,假设当i1≤n时,有|ai1|≤Bi1eK(i1-1)成立,由式(7)和引理1可知:
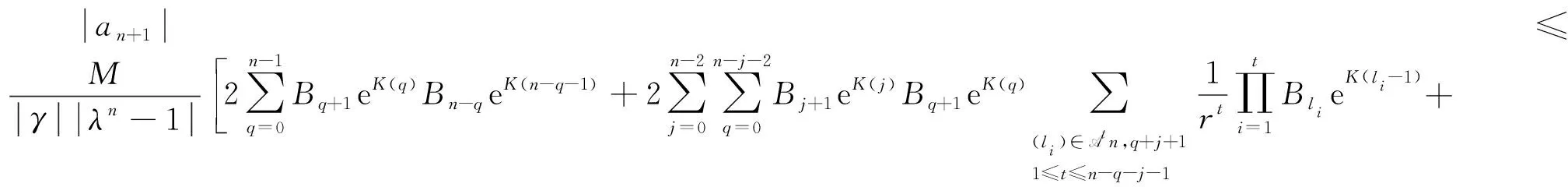
由于
K(q)+K(n-q-1)≤K(n-1),K(j)+K(q)+[K(l1-1)+K(l2-1)+…+K(lt-1)]≤K(n-t)≤K(n-1),K(j)+K(q)+[K(l1-1)+…+K(lt-1)]+[K(l1-1)+…+K(lτ-1)]≤K(n-1),K(j)+K(q)+K(n-j-q-2)≤K(n-2)≤K(n-1).
则
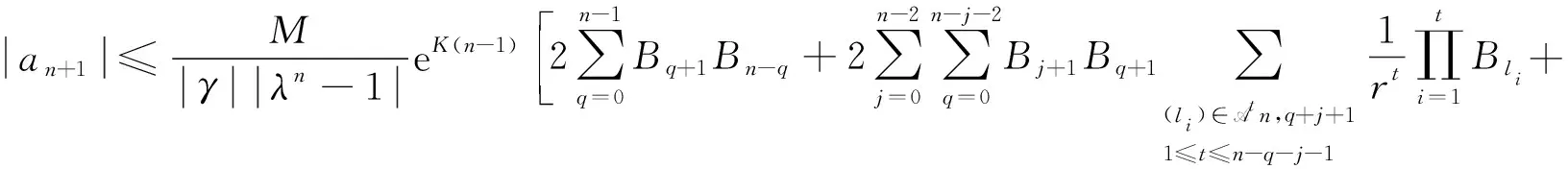
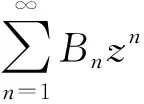
这说明在条件(C2)下,幂级数(3)的收敛半径至少是(ΛeB(θ)+ρ)-1,证毕.
讨论条件(C3)时,需要定义:

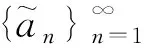

(12)
其中,
(13)
p是(C3)给定的,M的定义在定理1给出.
运用问题情境教学时,教师应根据课程标准的要求和学生的思维规律,把教学内容分解为诸多具有内在联系的细小问题,在教学过程中紧紧围绕这些问题展开。同时,教师根据不同类型的问题创设相关的情境悬念,引导学生积极联想和思考,增强他们的学习兴趣,激发他们产生解决问题的强烈愿望,使其达到想学、愿学和主动学习的目的。具体的问题情境教学思路为:确定目标→情境导入→提出问题→活动与探究→讨论与交流→得出结论→拓展延伸(提出新的问题或获取新的知识)。

γ(λn+1-λ)(n+1)an+1=Ψ(n,λ),n=1,2,…
(14)
若Ψ(lp,λ)=0,l=1,2,3,…时,方程(2)在原点的邻域内有一个形如
={1,2,3,…}
(15)

证明由定理1,令式(3)为y(z)的展开式,可得式(6)或式(14)成立.若对某些l,有Ψ(lp,λ)≠0时,则式(14)无法成立,因为当n=lp时,有λn+1-λ=λlp+1-λ=0,因此方程(2)没有形式解.

首先,注意到|λn-1|-1≤Γ,n≠lp,则由式(14)可得,
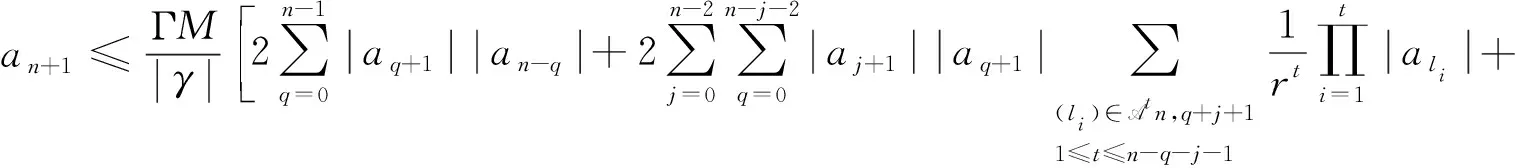
进一步,能够证明:
(16)

(17)
易验证式(17)满足
Θ(z,w;γ,Γ,M,r)=0,
(18)
这里函数Θ如式(9)所定义,类似于定理1,就证明了方程(18)存在唯一解析解F(z),使得F(0)=0,F′(0)=|η|≠0,因此式(17)在原点的邻域内收敛,由式(17)的收敛性及不等式(16),可知幂级数(15)在原点附近是收敛的,定理证毕.
定理3假设定理1或定理2成立,则迭代泛函微分方程(1)在原点的邻域内存在形如x(z)=y(λy-1(z))的解析解,其中y(z)是定理1和定理2所确定的解析解.
证明由定理1和定理2可知,辅助方程(2)有形如式(3)或式(15)的解析解y(z),满足y(0)=0,y′(0)=η≠0.故y-1(z)存在且在y(0)=0附近解析,定义
x(z)=y(λy-1(z)),
(19)
则y(z)在z=0附近是可逆且解析,由式(19)可知
x(0)=y(λy-1(0))=y(0)=0,

和
(20)
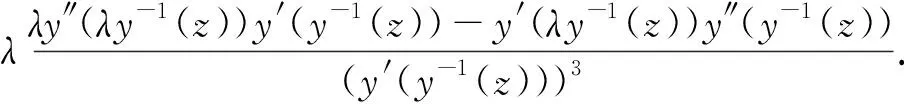
(21)
进一步,有
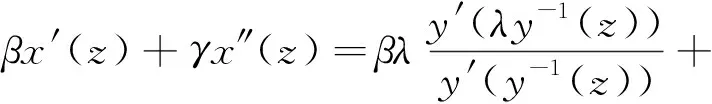
定理证毕.
3 例子
下面将通过一个例子,说明如何对一个形如式(1)的方程构造它的解析解.
考虑如下方程

(22)
其中
β=-1,γ=1.
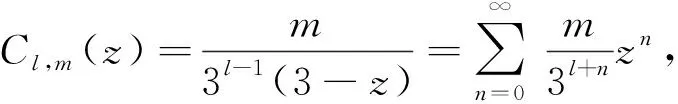
容易得出函数Cl,m(z)(l∈,m=0,1,2)和G(z)在|z|<3处解析.对于每一个m=0,1,2,序列
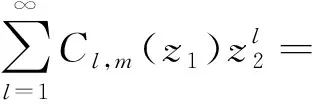
在给定的非零复数z1,z2处收敛,且
通过定理1,辅助方程

有一个解形如式(3),其中a1=η≠0,a2,a3,…是由式(6)决定的.则
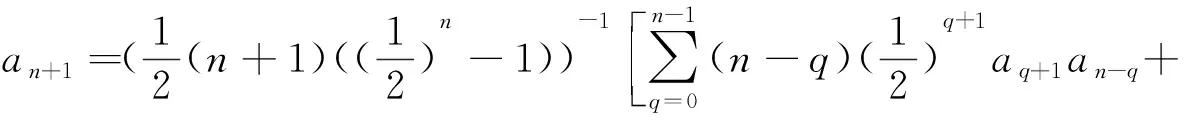
特别的,
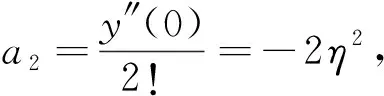
……
因为y(0)=0,y′(0)=η≠0.则y-1(z)在原点的邻域内解析,可以计算


……
更进一步,可得
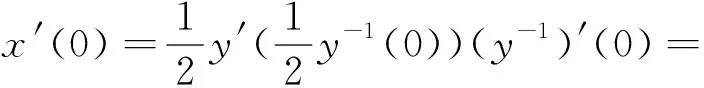
……
因此,在原点的邻域内方程(22)有一个解析解

