考虑磨损的全断面硬岩掘进机主轴承寿命计算

刘奇,卢振,霍军周,那鹏越

(1.大连理工大学 机械工程学院,辽宁 大连 116024;2.大连富士冰山自动售货机有限公司,辽宁 大连 116000)

全断面硬岩掘进机(Full Face Rock Tunnel Boring Machine,TBM)作为重要的隧道施工装备,在交通、水利、采矿等工程中得到了广泛应用。主驱动轴承作为掘进机传动系统的关键部件,承受掘进机的破岩载荷、冲击载荷、刀盘重力等复杂载荷,在保障掘进机正常工作中起到重要作用[1]。由于恶劣的工作环境,在隧道工程中,主轴承经常发生提前失效,进而造成施工事故及巨大的经济损失[2-3]。TBM主轴承是典型的三排圆柱滚子轴承,对不同工程施工后的TBM主轴承的拆解检测发现,主轴承的滚子、滚道存在严重磨损[4-5],一些学者对其他应用中的三排圆柱滚子轴承进行检测和铁谱分析发现,轴承滚子与滚道也存在磨损问题[6-7]。因此,开展TBM主轴承的疲劳寿命预测,对转盘轴承的设计制造以及掘进机施工安全具有重要意义。

与中小型轴承相比,TBM主轴承转速低、结构尺寸大、载荷分布复杂、服役寿命难以预测。计算主轴承疲劳寿命时需得到其载荷分布。目前,国内外学者主要通过建立解析模型与有限元模型[8]对大型轴承载荷分布进行计算:文献[9-11]使用弹簧单元模拟滚子与滚道的接触,建立了简化的转盘轴承力学模型;文献[12]研究了弹簧单元数量对大型轴承载荷分布计算结果的影响,发现当非线性弹簧数量为8时计算精度最高;文献[13]建立转盘轴承力学解析模型,求解转盘轴承的载荷分布,并与有限元模型对比验证了算法的正确性。

目前,转盘轴承寿命预测方法主要有以下3种:1)统计回归模型,多数研究基于L-P寿命理论,考虑多种因素对寿命公式进行修正;2)状态监测,由于TBM工作空间狭小,故障信号提取困难,该方法难以在TBM主轴承中得到应用;3)力学模型,通过力学模型从机理上研究轴承失效,相比于状态监测方法具有更明确的物理意义,逐渐受到广大学者的关注。

力学模型主要有断裂力学与损伤力学2种模型[14]:1)断裂力学模型关注的是裂纹萌生后的扩展阶段,不适用于裂纹萌生周期长的滚动轴承;2)损伤力学模型研究材料在各种加载条件下,物体中的损伤演化直至材料破坏的过程[15],更适用于轴承失效分析。国内外学者在力学模型方面已开展了大量研究:文献[16]结合损伤力学与有限元法,对材料在循环载荷下的滚动接触疲劳进行预测;文献[17]在损伤力学的基础上,考虑了损伤与材料弹塑性行为的耦合关系,计算疲劳损伤演化;文献[18]以连续损伤力学为基础,将最大接触应力区进行二维简化并构建损伤演化云图计算轴承寿命。

目前,针对轴承疲劳寿命的力学模型主要集中在小型轴承上,对TBM主轴承等大型转盘轴承的分析较少,且没有考虑磨损等因素对疲劳寿命的影响。本文以某4.8 m级TBM主驱动轴承为研究对象,提出一种考虑磨损的TBM主轴承寿命预测模型:首先,建立主轴承载荷分布计算模型并通过有限元模型进行验证;然后,通过建立有限元模型提取轴承接触载荷并建立滚子接触分析局部模型;最后,基于主轴承运动学和考虑表面粗糙度影响的磨损理论建立滚子磨损模型,同时构建接触疲劳损伤演化模型,计算主轴承疲劳寿命。

1 TBM主轴承载荷分布计算

1.1 载荷分布解析模型

由TBM主轴承受载情况及变形协调关系,对主轴承进行静力学分析并建立主轴承载荷分布的解析模型,建模时做以下假设:1)由于TBM转速很低,忽略离心力对载荷分布的影响[19];2)由于轴承内、外圈的刚度远大于滚子刚度,假设轴承内、外圈不发生变形;3)忽略螺栓、油孔、保持架等的影响。

本文研究的4.8 m级TBM主轴承的结构及受力图如图1所示,该轴承为三排四列圆柱滚子轴承,滚子采用圆弧修形。主轴承有3个外圈,3个外圈通过螺栓连接,第1外圈与机头架连接,因此可以认为外圈固定,内圈承受轴向力Fa、径向力Fr及倾覆力矩M。在载荷作用下,内圈会产生轴向位移δa、径向位移δr及倾角θ。

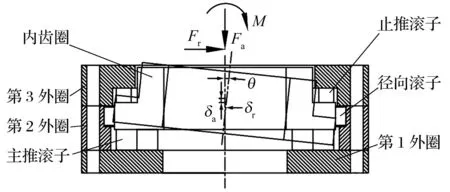
图1 TBM主轴承结构及受力图

为便于定义滚子在外圈上的位置,在主轴承中心建立极坐标系,极角用ψ表示,如图2所示,则第j个滚子的方位角为

图2 滚子方位角示意图

(1)

式中:Z为单排滚子数量。

在载荷作用下,内圈产生位移和倾角,主推滚子与外滚道之间的弹性趋近量为

(2)

滚子所承受的载荷为

(3)

k=Dwu/Dpwu,

式中:Dpwu为主推滚子的滚子组节圆直径;Ga为轴承轴向游隙;Ku为主推滚子与滚道的载荷-变形常数;Dwu为主推滚子直径;η为弹性常数;Lwe为主推滚子有效长度。

同理可得止推滚子与滚道之间的弹性趋近量为

(4)

滚子所承受的载荷为

(5)

式中:Dpwo为止推滚子的滚子组节圆直径;Ko为止推滚子与滚道的载荷-变形常数,计算方式同(3)式。

在径向力作用下,内圈会产生一个位移,径向滚子与滚道之间的弹性趋近量为

(6)

同理可得在任意位置径向滚子所承受的载荷为

(7)

式中:Gr为轴承径向游隙;Kr为径向滚子与滚道的载荷-变形常数。

在载荷作用下,主轴承处于平衡状态,内圈受力平衡方程为

(8)

将(1)—(7)式代入(8)式建立非线性方程组,利用牛顿迭代法(采用有限差分法逼近雅可比矩阵以解决矩阵奇异问题)可求得轴向位移δa、径向位移δr及倾角θ,再使用Matlab由(3),(5),(7)式得到主轴承的载荷分布。

1.2 模型验证

本文研究的4.8 m级TBM主轴承的主要结构参数见表1,主轴承主要承受的外载荷为:轴向力Fa=14 600 kN,径向力Fr=4 225 kN,倾覆力矩M=23 687 kN·m。

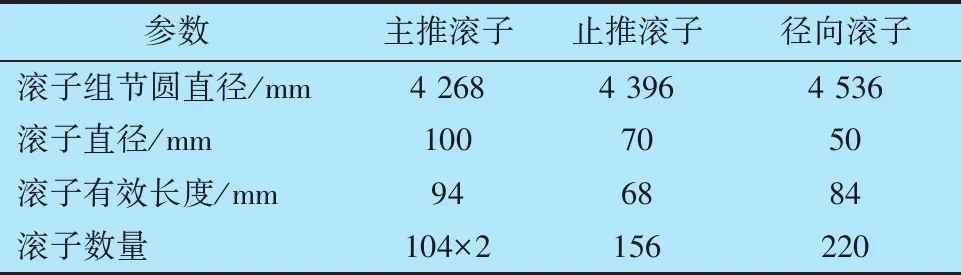
表1 4.8 m级TBM主轴承结构参数

为验证解析模型的正确性,使用ANSYS对轴承进行分析,使用弹簧单元模拟滚子与滚道的接触,内、外圈采用实体单元SOLID186。由于轴承外圈固定,对外圈施加固定约束。在内圈中心点建立关键点并将其设置为主节点,使用MASS21单元进行网格划分,将主轴承内圈自由度与其进行耦合。

在主节点上施加载荷并进行求解,有限元分析得到的滚子载荷分布及其与解析模型的对比如图3所示:

图3 滚子载荷分布

1)2种模型下,主推滚子、止推滚子、径向滚子接触载荷平均误差分别为1.3%,16.8%,2.7%,说明了解析模型的正确性。有限元分析结果会在解析模型附近波动,这是由于有限元分析将内、外圈离散为有限的单元体且接触载荷由弹簧单元获得,当计算结果满足收敛条件时,接触载荷值为计算结束所调整的值。

2)在外载荷作用下,主推滚子受载处止推滚子不受载。

3)解析模型得到的主推滚子最大载荷为367 032 N,位于180°处;止推滚子最大载荷为34 156 N,位于0°处;径向滚子最大载荷为78 434 N,位于0°处。说明主推滚子受载最大,将最先发生失效。

2 滚子接触分析

由1.2节的分析结果可知,止推滚子和径向滚子承受的最大接触载荷与主推滚子相比较小,主轴承的疲劳寿命主要取决于主推滚子与滚道的接触疲劳寿命。建立主推滚子1/2模型,分析其接触特性。为保证计算结果的准确性,同时提高有限元仿真效率,将主推滚子接触区网格细化为0.5 mm,其他部分网格尺寸为4 mm,单元数量为87 926,滚子局部有限元模型如图4所示。 根据实际工况对主轴承进行边界条件(图5)施加: 外圈固定,施加全固定约束,侧面施加对称位移约束;由于主轴承有2列主推滚子,在主推滚子和内圈上施加1/4最大接触载荷;滚子与滚道的接触设为摩擦接触, 其他部分设为绑定接触。

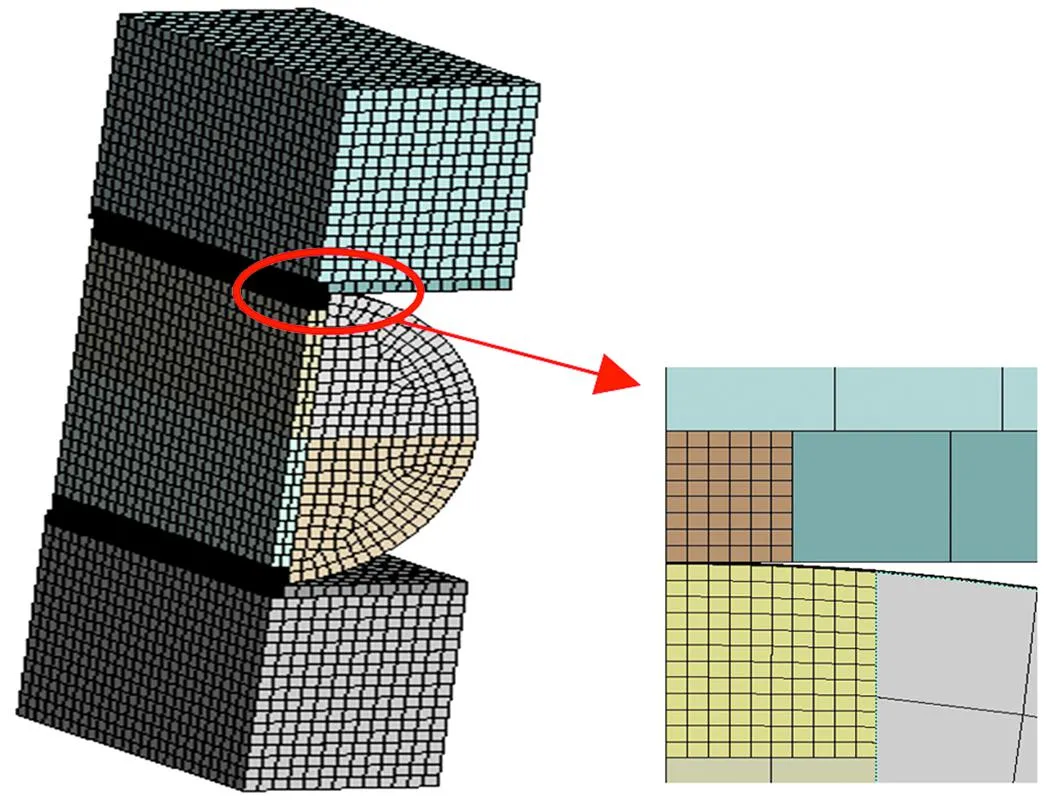
图4 主推滚子局部有限元模型

图5 边界条件

ANSYS接触问题中需要自定义接触刚度因子FKN,而FKN的选取会对接触产生影响,进而影响寿命的计算,不同FKN值下主推滚子的最大正交剪切应力及接触应力如图6所示:随FKN值增大,滚子最大正交剪切应力及接触应力逐渐增大,当FKN值大于4时, 最大正交剪切应力及接触应力趋于稳定。综合考虑计算精度与计算效率,在主推滚子接触有限元分析及寿命计算中,将FKN值设定为4。

图6 不同FKN值下主推滚子的最大正交剪切应力及接触应力

主推滚子与滚道的等效应力云图如图7所示:1)等效应力主要出现在接触区表面下方, 说明次表面也是易损伤位置;2)最大等效应力为765.45 MPa,低于屈服强度(1 834.3 MPa),可以认为材料处于弹性状态。

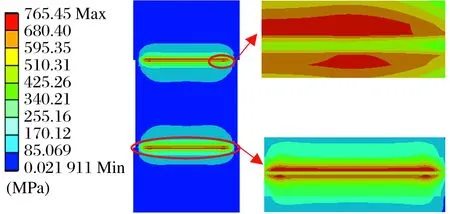
图7 主推滚子与滚道的等效应力云图

主推滚子沿素线方向的接触应力如图8所示:接触应力沿素线方向分布均匀,在边缘处出现应力集中现象,最大接触应力为1 253.6 MPa。

图8 主推滚子接触应力

3 考虑磨损的TBM主轴承寿命预测

由于主推滚子承受最大的接触载荷,因此相对于止推滚子和径向滚子,主推滚子最先失效。圆柱滚子轴承在服役过程中无法避免滚子的自旋滑动,导致滚子发生磨损并改变滚子的几何形状,进而改变滚子与滚道之间的接触应力,加速主轴承的接触疲劳失效。

3.1 考虑粗糙度影响的磨损模型

Archard磨损模型用磨损体积反应材料的磨损情况,被广泛应用于计算材料磨损,其认为磨损与法向压力、屈服强度及相对滑动有关,微分形式为

(9)

式中:V为磨损体积;K为磨损系数;F为接触压力;σs为屈服强度;s为相对滑动距离。

相对于磨损体积,磨损深度可以更直观地表示材料磨损情况,可直接应用于模型的磨损计算。对(9)式进行积分后,两端同时除以接触面积A,可得磨损深度为

(10)

式中:P为接触应力,通过有限元模型得到;v为速度参数;t为时间。

由于内圈旋转,外圈固定,滚子的运动为随内圈的公转和自身旋转,因此会发生相对滑动。由于相对滑动,滚子与滚道间会发生磨损,因此以滚子与滚道作为研究目标,进行运动分析以获得相对滑动速度,进而求解磨损模型。假设滚子与滚道在节圆处的相对运动为纯滚动[19],滚子运动如图9、图10所示。

图9 滚子相对滑动

根据主轴承的运动情况,滚子在纯滚动两点的绝对速度为

(11)

(12)

式中:ωg,ωz分别为滚子的公转角速度和自转角速度。

由纯滚动条件可知,A,B两点处的绝对速度与内圈相同,则

(13)

(14)

式中:ωn为内圈角速度。

根据(11)—(14)式可得滚子与内、外圈的相对滑动速度为

(15)

(16)

式中:r为滚子半径。

将主轴承的结构参数和运动参数代入(15),(16)式即可得到速度参数。

文献[20]的研究发现粗糙度会影响磨损,因此在文献[21]研究的基础上,提出了考虑表面粗糙度的磨损模型

(17)

式中:K为磨损系数;Cw,iw为表面粗糙度常数;a,b,c为材料参数。

3.2 基于损伤力学的主轴承寿命预测

连续损伤力学引入损伤变量D表示材料的损伤,可表示为

(18)

定义损伤单元的弹性模量为

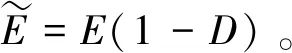
(19)

在滚动接触情况下,次表面裂纹的形成和扩展由剪切应力引起[22],由接触分析可知材料处于弹性状态,故将剪切应力作为滚动接触疲劳的驱动力,损伤演化方程为

(20)

Δτ0=2τmax,

式中:N为应力循环次数;τmax为最大正交剪切应力;τR为抵抗应力,取6 720.48 MPa;m为材料疲劳参数,取10.5。

由于轴承疲劳是典型的高周疲劳,选择1个迭代步长需要进行大量计算,计算成本极高且效率低,因此参考文献[23-24]提出的跳跃周期法进行计算,如图11所示。该方法将若干次应力循环视为一个磨损周期ΔN,由于磨损导致的体积变化很小,因此认为每个磨损周期内的应力分布保持不变,将1 500 h划分为一个磨损周期,计算每个周期内的损伤D与磨损深度h并分别累积

(21)

图11 跳跃周期法示意图

式中:i为第i个周期;Δh为每个循环的磨损深度;ΔN为磨损周期;ΔD为每个循环的损伤。

损伤变量D累积至1时,说明已发生疲劳破坏,结束运算;否则根据磨损模型更新模型几何轮廓,继续计算磨损及损伤量并累积。由于沿滚子素线上各点具有不同的滑动速度,且各截面损伤值也不同,因此对滚子进行切片处理,考虑滚子尺寸,沿滚子素线每隔1 mm进行切分,共切分为100片,分别计算每个切片的接触应力与剪切应力,代入(21)式可得到相应的磨损深度与损伤。

3.3 结果分析

滚子接触应力以及磨损深度的变化分别如图12、图13所示,结合图12和图13可知:1)滚子中心处由于速度为0,不发生磨损,磨损深度从滚子中心到两端先增大后减小,在距离滚子36 mm处,磨损深度最大,最大磨损深度为39.66 μm,这导致滚子最大接触应力从最初边缘处的1 253 MPa增大至中心处的1 584 MPa;2)随着磨损的发生,滚子有效接触长度由94 mm增大至96 mm,这导致滚子整体接触应力减小。

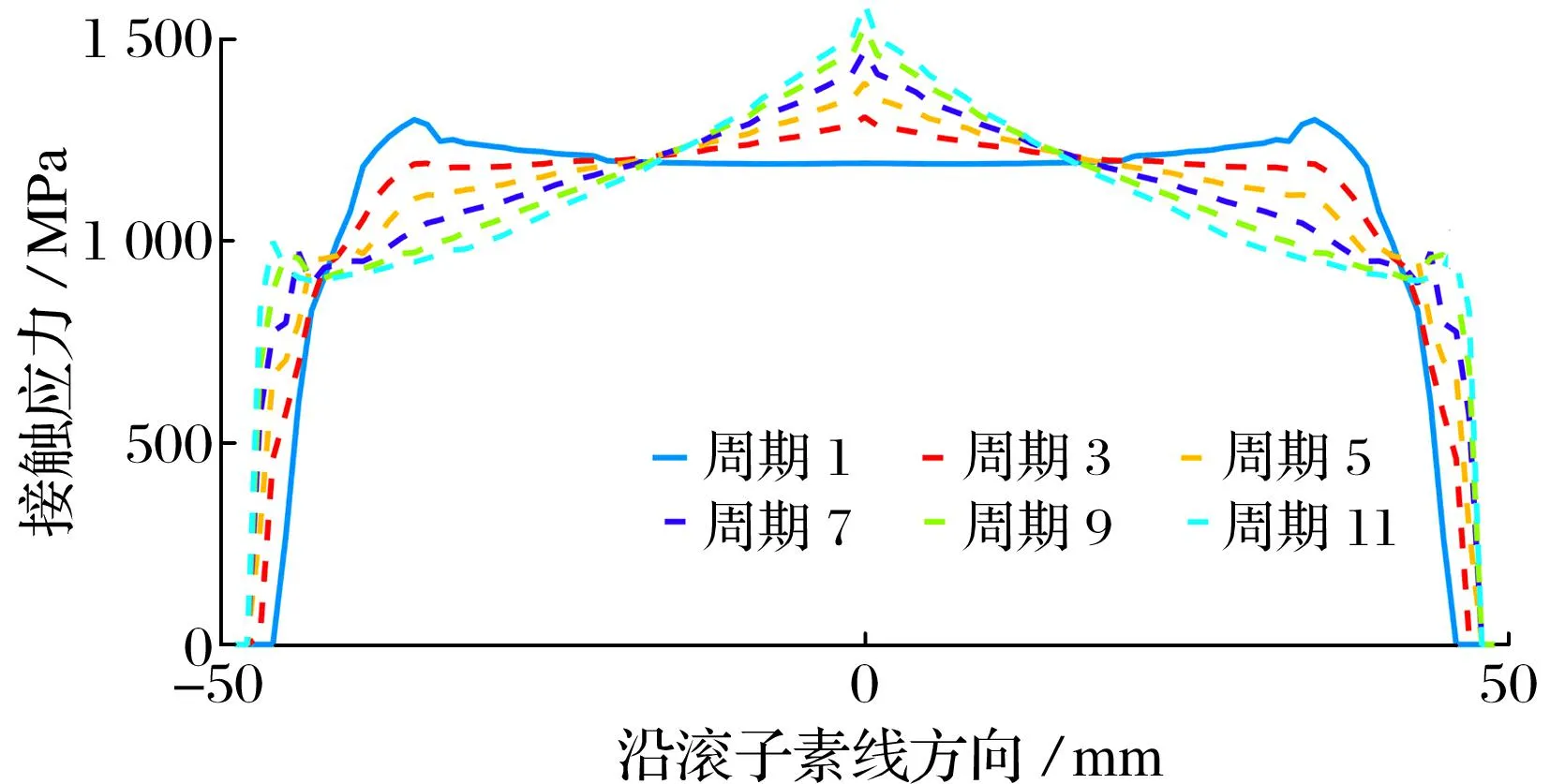
图12 滚子接触应力

图13 滚子磨损深度

提取每个磨损周期内的最大损伤量进行累积,损伤累积如图14所示:在经过4.5×106次循环后,损伤D达到0.3,损伤开始显著上升,导致滚子快速发生失效。根据相关学者开展的轴承寿命试验与有限元分析[25],发现损伤D为0.3时计算得到的轴承寿命与试验得到的轴承寿命吻合度较好。因此,轴承寿命可以设定为损伤D为0.3时的累积磨损周期,为15 778 h。

图14 损伤累积

4 结束语

针对TBM主轴承在恶劣的服役环境下会因磨损疲劳复合作用导致寿命计算困难的问题,提出一种考虑磨损的TBM主轴承寿命预测模型。首先,建立了主轴承载荷分布计算模型确定主推滚子载荷;然后,建立滚子与滚道接触的局部有限元模型获得滚子接触特性;最后,基于Archard磨损理论与连续损伤力学理论对主轴承疲劳寿命进行预测。以某4.8 m级TBM主轴承为研究对象开展寿命研究,结果表明滚子中心处不发生磨损,磨损深度从滚子中心到两端先增大后减小,导致最大接触应力从最初边缘处的1 253 MPa增大至中心处的1 584 MPa,滚子有效接触长度从94 mm增大至96 mm,计算得到主轴承寿命为15 778 h。本文的寿命预测方法可为该类轴承的设计和应用提供参考。