考虑瓦块子结构的可倾瓦轴承广义完整动特性系数研究

闫岗,刘洋洋,齐洪柱,佟晓敏,袁小阳

(1.中国工程物理研究院 材料研究所,四川 绵阳 621907;2.西安交通大学 现代设计及转子轴承系统教育部重点实验室,西安 710049)

可倾瓦轴承具有相互独立的瓦块,这些瓦块可随着载荷的波动和工作转速的变化绕其瓦背的支点做自适应摆动,从而减小切向力。因此该类轴承的稳定性更高,为旋转机械的安全、稳定运行提供保障,在各类大型机组上广泛应用。

随着现代工业技术的进步,轴承转子系统逐渐向高速化、重载化方向发展,对系统的振动稳定性提出更高的要求。在研究小振幅转子系统振动时,通常将液膜简化为线性弹簧和阻尼器,将线性化后的弹簧及阻尼器系数称为液膜的刚度系数和阻尼系数,即动特性系数,动特性系数的计算精度直接影响转子系统振动分析的准确性。目前应用广泛的可倾瓦轴承动特性系数的表征方法为常规8系数[1],此方法最早由文献[2]提出,且提出了计算动特性系数的瓦块叠加法。文献[3]利用动特性系数计算了可倾瓦轴承的动力学响应。但在理想情况下采用常规8系数分析轴系稳定性时会得出绝对稳定的结果,这显然与现实情况相悖。因此,需要探索新的可倾瓦轴承动特性系数表征方法。可倾瓦轴承的动特性系数会随轴颈涡动频率及扰动频率的变化而变化,文献[4]通过理论与试验研究了瓦块的振动频率和摆动频率对可倾瓦轴承动特性系数的影响,提出频变动力学模型。文献[5]研究了核主泵水润滑轴承的频变动力学性能,指出频率变化对轴承动特性的影响较大。文献[6]的试验结果表明可倾瓦轴承动特性与瓦块摆动频率密切相关。文献[7]从理论和试验方面研究了激振频率对可倾瓦推力轴承动特性的影响。文献[8]系统研究了扰动频率对可倾瓦轴承动特性的影响。与常规8系数相比,频变8系数在准确性方面具有一定优势,但可倾瓦轴承瓦块的摆动自由度同样不可忽略。文献[9]基于动力学参数和自由度关系提出可倾瓦轴承需要更多系数描述其动特性的观点,即刚度系数和阻尼系数的个数需要增加。文献[10]通过研究轴颈与瓦块的耦合运动,指出不应忽略瓦块对轴承动特性的影响。文献[11]在对四瓦可倾瓦径向滑动轴承动特性进行试验后,指出忽略瓦块摆动的惯性会给可倾瓦轴承动特性系数的计算带来较大误差。

综上可知,可倾瓦轴承动特性是油膜动特性和瓦块摆动的综合体现。因此,本文提出考虑瓦块子结构的可倾瓦轴承广义完整动特性系数表征方法,旨在提高动特性系数的计算精度,完善相关理论模型,计算得到的瓦块动特性系数可用于分析瓦块的摆振特性及稳定性问题,为实际机组的瓦块失稳现象提供理论依据。同时研究轴承结构参数和运行工况对可倾瓦轴承动特性系数的影响,为可倾瓦轴承的结构设计提供参考。

1 广义完整动特性系数模型

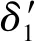
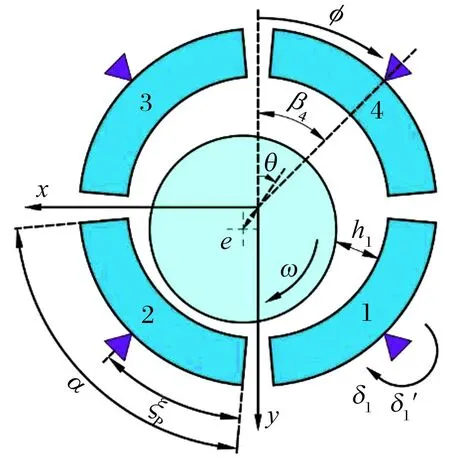
图1 可倾瓦轴承计算坐标系

瓦包角为瓦块两边缘延长线的夹角,以四瓦可倾瓦轴承为例,其瓦包角极值为90°;支点位置角β为周向起始位置至支点处的周向角;支点系数ζ为瓦块进液边至支点位置的周向角与瓦包角的比值。支点系数和瓦包角会影响承载液膜的进口边角,进而对液膜压力分布及承载力产生影响。

长径比用于表征轴承长度L与直径D之间的关系,对于可倾瓦轴承,轴承长度即为瓦块长度,即

(1)

式中:LP为瓦块长度;R为轴颈半径。

间隙是影响可倾瓦轴承性能的关键因素,用于表征可倾瓦轴承间隙的重要结构参数有间隙比和预载荷系数。其中间隙比ψ为瓦块径向间隙与轴承半径之比。

可倾瓦轴承的间隙有瓦块径向间隙和轴承径向间隙2种,预载荷系数可以表征2种间隙之间的关系,是可倾瓦轴承设计和计算的重要结构参数之一。假设轴承瓦块支点为刚性且位于同一支点圆上,预载荷系数与瓦块支点的径向位置和瓦面的曲率半径有关,如图2所示。可倾瓦轴承预载荷的大小可用预载荷系数A表示,即

(2)

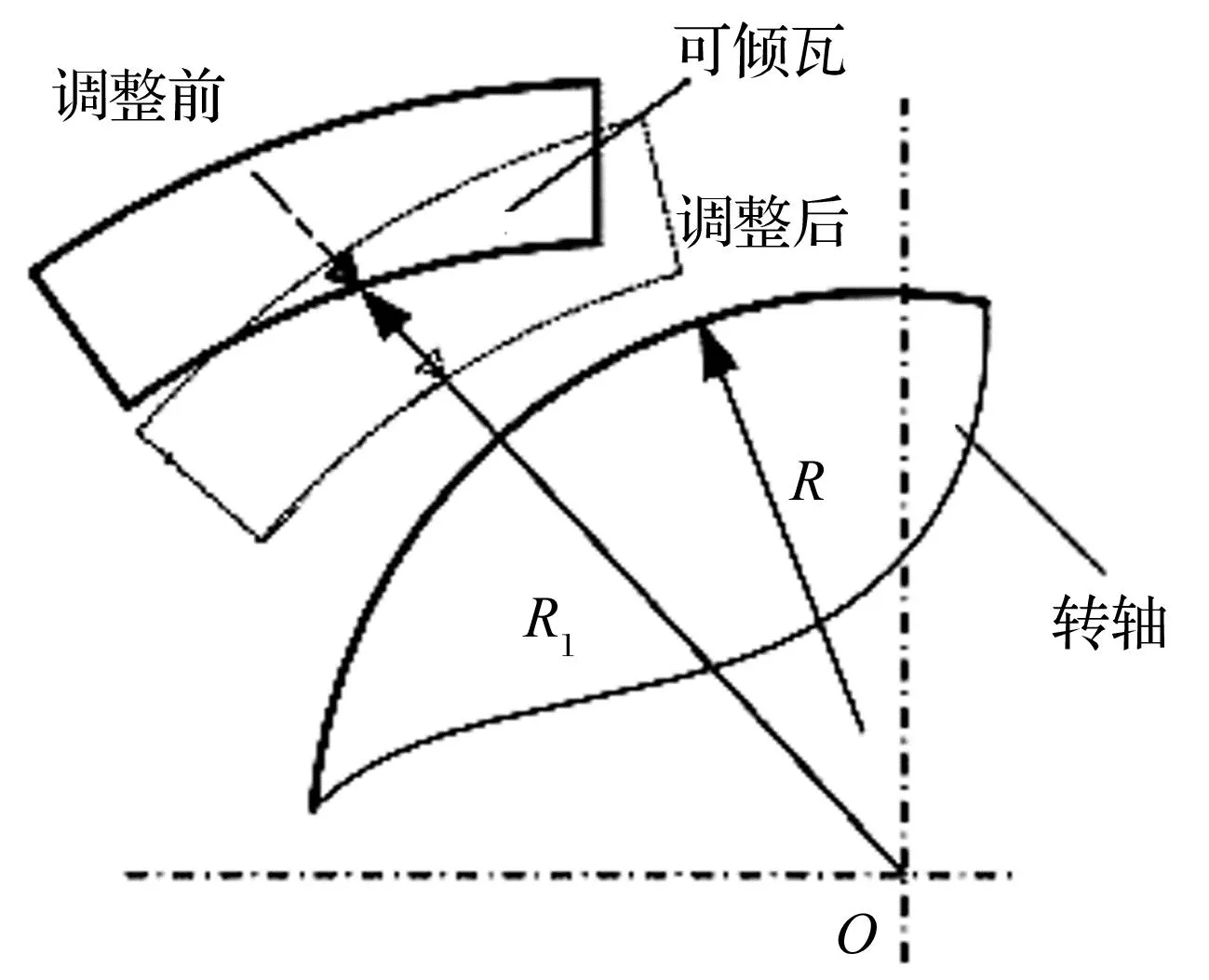
图2 可倾瓦轴承瓦块预载荷系数的定义

cb=R1-R,

cp=R2-R,

式中:cb为轴承径向间隙;cp为瓦块径向间隙;R1为支点圆半径;R2为瓦面的曲率半径。

在等温、不可压缩、无惯性流动的条件下,考虑紊流效应的雷诺方程为

(3)

式中:h为瓦块液膜厚度;kφ为周向紊流系数;p为液膜压力;z为轴向坐标;kz为轴向紊流系数;μ为润滑介质动力黏度;t为时间。

瓦块的液膜厚度方程为

h=cp-(cp-cb)cos(β-φ)+ecos(φ-θ)+Rδsin(β-φ)。

(4)

采用低黏润滑介质的旋转机械、高速透平机械以及大容量发电机组中的轴承润滑介质均存在由层流过渡至紊流的可能性。因此,为扩大模型的适用范围,提高模型的计算准确度,本文在理论模型中考虑了紊流效应,采用Ng-Pan紊流模型[12]。紊流系数kφ,kz为

(5)

式中:Re为有效雷诺数。

采用有限差分法求解雷诺方程得到瓦块压力分布,再通过压力积分得到第i块瓦的液膜力分量fxi,fyi,即

(6)

式中:pi为第i块瓦的液膜压力;φin为进液边位置角;φout为出液边位置角。

将各瓦块的液膜力分量叠加即可得到轴承的液膜力分量fx,fy,即

(7)

式中:n为瓦块数。

第i块瓦的液膜力矩Mpi为

(8)

本文以瓦间承载的四瓦可倾瓦轴承为研究对象,在计算其广义完整动特性系数时,除轴颈在x和y方向的速度扰动与位移扰动外还需考虑瓦块子结构的扰动,即4块瓦的摆角扰动和摆速扰动,此时共有6个位移扰动参数,6个速度扰动参数,2个力参数,4个力矩参数。由此,便可导出四瓦可倾瓦轴承的72个动特性系数。

将瓦块液膜力和力矩均看作是平衡位置附近的位移和速度的扰动函数,当轴颈和瓦块同时在其平衡位置附近做微小扰动时,利用泰勒级数将液膜力和力矩展开,并略去二阶以上的高阶小量,四瓦可倾瓦轴承在静平衡位置附近的液膜力及力矩增量可近似表述为

(9)

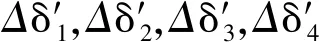
由定义可知各动特性系数的表达式,广义刚度系数矩阵K和广义阻尼系数矩阵C为

(10)

(11)

采用差分概念法计算动特性系数时应合理选择扰动量,若扰动量过大会远离线性化假设;若扰动量过小,则计算误差较大,从而影响计算精度。文献[13]对差分概念法求解动特性系数的精度进行了研究,指出量纲一的扰动量取0.01为宜。因此,本文位移扰动取0.01cp,摆角扰动取0.01δmax,速度扰动取0.01ωcp,摆速扰动取0.01ω。

δmax为轴颈位于轴承中心处,瓦块与轴颈不发生碰撞时瓦块所能达到的最大摆角,即

(12)

本文提出的广义完整动特性系数内涵有两点:将常规8系数模型的两自由度研究对象转变为考虑瓦块子结构的6自由度系统(针对四瓦可倾瓦轴承);扰动量不仅限于力与位移,还包括了瓦块的力矩与摆角,这是一种交叉项更复杂的新模型。该模型下常规的轴颈扰动交叉项、位移扰动与力矩之间的广义交叉项、摆角扰动与力之间的广义交叉项,呈现的规律将有很大不同。

本文计算动特性系数时,轴承的结构和运行参数见表1,在后续研究某一参数对动特性系数的影响时,其余参数均保持表1的数值不变。

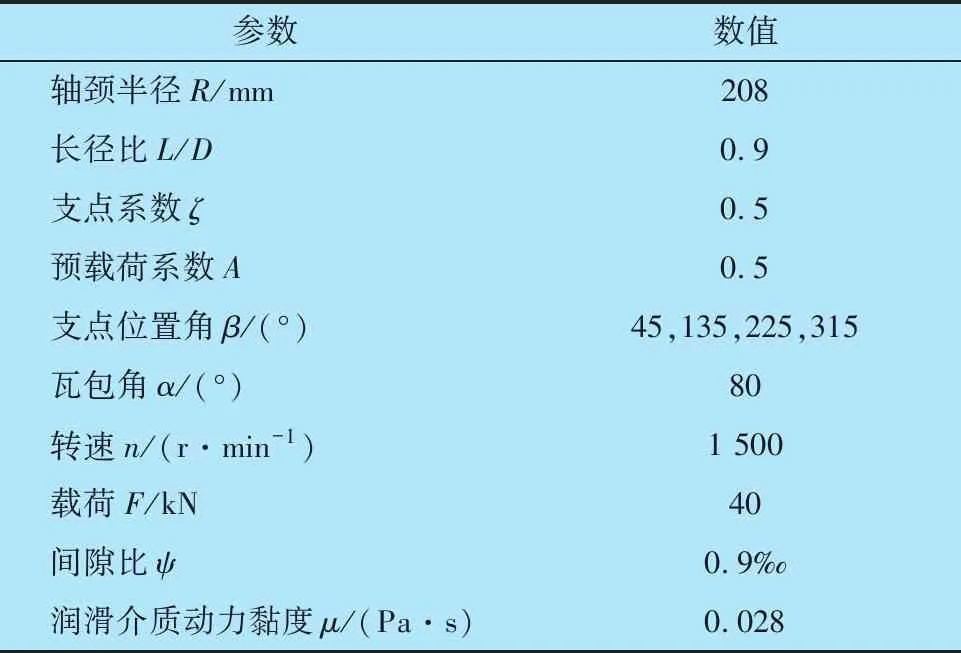
表1 轴承的结构和运行参数

2 模型可靠性验证

(13)式和(14)式分别为计算得到的一组广义完整刚度系数和阻尼系数:由轴颈扰动引起的x和y方向上的主刚度系数相同,交叉刚度系数大小相同,符号相反,两承载瓦(1#瓦和2#瓦,下同)的角刚度系数相同,两非承载瓦(3#瓦和4#瓦,下同)的角刚度系数相同,承载瓦的角刚度系数比非承载瓦的大;阻尼系数的规律与刚度系数类似,轴颈扰动引起的主阻尼系数相同,交叉阻尼系数互为相反数,两承载瓦的角阻尼系数相同,两非承载瓦的角阻尼系数相同,承载瓦的角阻尼系数比非承载瓦的大。

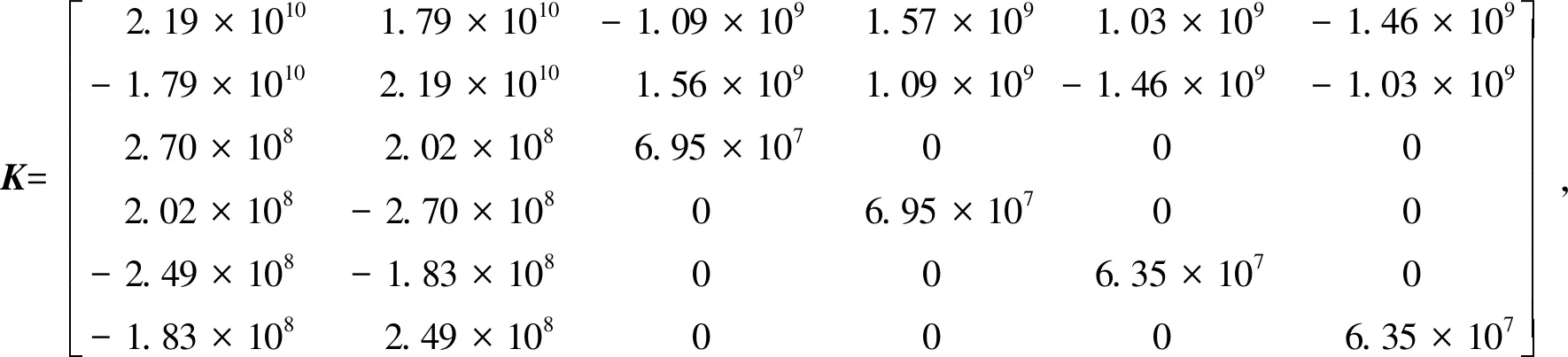
(13)

(14)

为验证本文模型计算结果的正确性,将上述结果与文献[14]瓦间承载的轴承动特性系数进行对比。以文献[14]中一组量纲一的动特性系数为例:主刚度系数Kxx=20.25,Kyy=19.98,交叉刚度系数Kxy=-12.98,Kyx=14.19。主刚度系数符号相同,交叉刚度系数符号相反;文献[14]根据结构及运行参数的不同,交叉阻尼系数与主阻尼系数相差1～3个数量级,与本文的计算结果相符。

文献[15-16]的结果表明:考虑瓦块转动惯量对可倾瓦轴承动特性系数进行研究发现,交叉刚度系数与交叉阻尼系数不再相同,而是随着转动惯量的增加分别向正负2个方向增大,呈相反数的关系;多组计算数据表明转动惯量越大,交叉刚度系数和交叉阻尼系数的正负差值越大,但均互为相反数,转动惯量的大小对交叉刚度系数和交叉阻尼系数互呈相反数这一规律并无影响,这与本文的结果一致。

为进一步验证本文动特性系数计算的可靠性,分别采用有限差分法和动特性系数法计算了四瓦可倾瓦轴承在小扰动下的轴心轨迹和各瓦块摆角。动特性系数法利用本文模型的72个动特性系数计算小扰动下可倾瓦轴承在静平衡位置附近瓦块的液膜力和力矩增量,进而根据运动方程得到轴颈的轴心轨迹和各瓦块的摆角;有限差分法直接利用有限差分方法求解雷诺方程得到液膜的压力分布,再利用Simpson积分法得到瓦块的液膜力和力矩。2种算法计算出的轴心轨迹和各瓦块摆角如图3和图4所示。

图4 四瓦可倾瓦轴承的各瓦块摆角

由图3和图4可知:有限差分法和动特性系数法计算出的轴心轨迹和各瓦块摆角在到达稳态后的时域响应几乎重合,但有限差分法计算出的轴心轨迹和各瓦块摆角幅值略小于动特性系数法。利用动特性系数法(线性动力学)计算时忽略了轴承间隙的约束作用,不能很好地反映轴承的润滑和动力学性能,轴承转子系统具有非线性效应, 因此计算结果比有限差分法的大, 且随着扰动量的增大两者之间的差值也会越来越明显。 但在小扰动下2种方法的计算结果的一致性较好,广义完整动特性系数计算的正确性得以验证。

3 计算结果与讨论

3.1 载荷的影响

载荷对轴颈刚度系数和阻尼系数的影响如图5所示:刚度系数、阻尼系数的绝对值均随载荷的增加而增大;主刚度系数Kxx与Kyy、主阻尼系数Cxx与Cyy的大小相同且曲线重合;交叉刚度系数Kxy与Kyx、交叉阻尼系数Cxy与Cyx的大小相同,方向相反,随着载荷的增加分别向正负2个方向增大,曲线关于x轴对称;当载荷小于200 kN时,各刚度系数、阻尼系数的变化很小,但当载荷大于200 kN后,各刚度系数、阻尼系数的绝对值随载荷增加而增大的趋势明显增大,当载荷从200 kN增到800 kN时,主刚度系数和主阻尼系数分别为原来的1.4倍和1.3倍,交叉刚度系数绝对值为原来的1.28倍;交叉刚度系数绝对值的变化规律与主刚度系数相同,但变化幅度较小,交叉阻尼系数远小于主阻尼系数,与主阻尼系数相差3个数量级,随载荷增加的变化非常小。

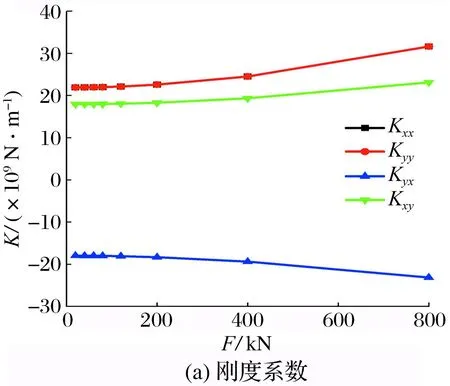
图5 载荷对轴颈刚度系数和阻尼系数的影响

载荷对瓦块角刚度系数和角阻尼系数的影响如图6所示:1#瓦与2#瓦的角刚度系数、角阻尼系数的大小均相同,随着载荷的增加而增大;3#瓦与4#瓦的角刚度系数、角阻尼系数的大小均相同,随着载荷的增加而减小;当载荷从200 kN增到800 kN时,承载瓦的角刚度系数和角阻尼系数分别为原来的2.34倍和2.16倍,非承载瓦的角刚度系数和角阻尼系数分别为原来的48%和55%。非承载瓦的角刚度系数、角阻尼系数减小的原因是随着载荷的增加,静平衡位置逐渐下移,导致非承载瓦的工作间隙增大,说明非承载瓦在大工作间隙下容易出现失稳现象。可倾瓦轴承在工作过程中发生过非承载瓦失稳损伤故障[17],这也印证了上述理论结果的正确性。

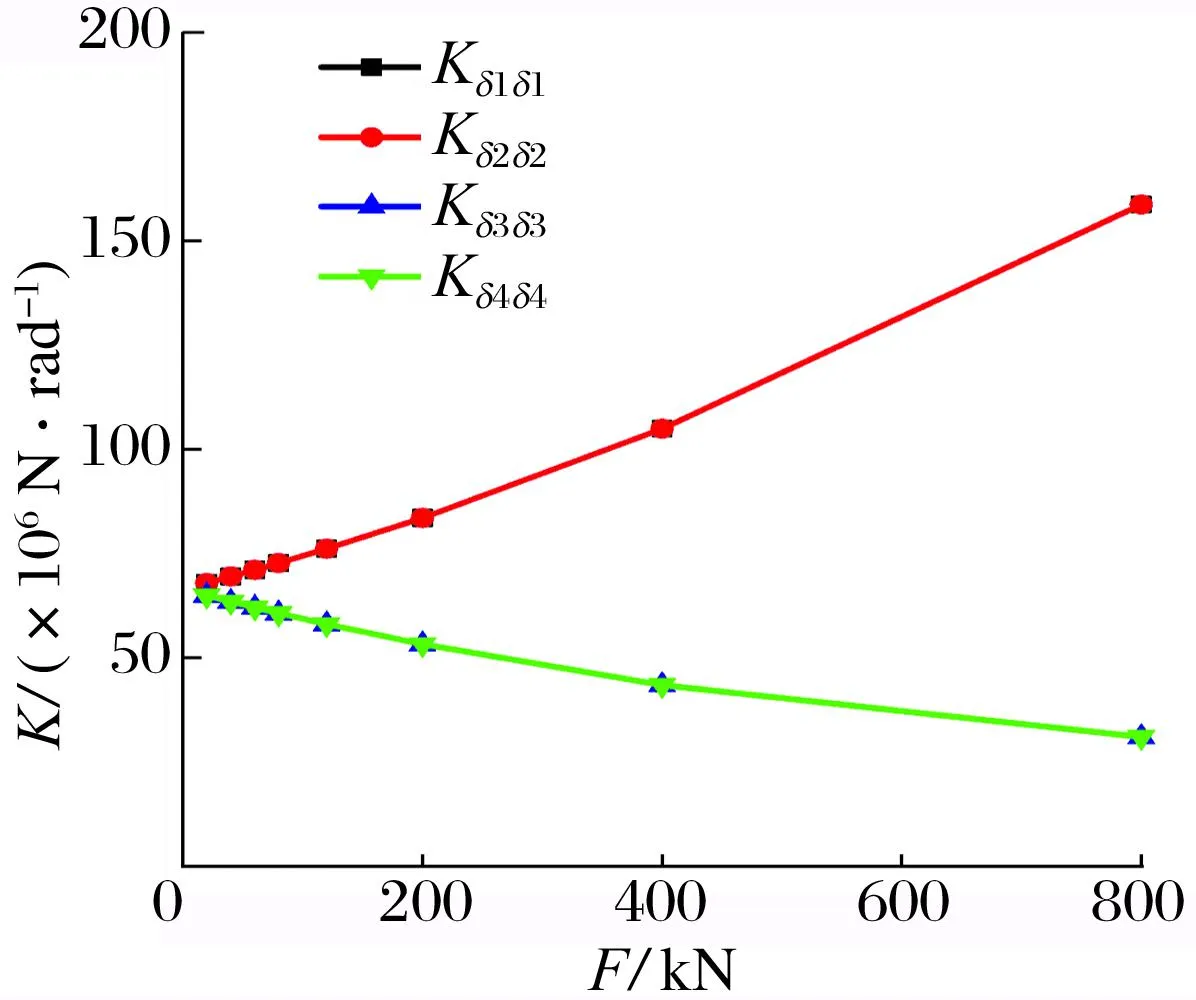
(a) 角刚度系数

3.2 转速的影响

转速对轴颈刚度系数和阻尼系数的影响如图7所示:主刚度系数Kxx与Kyy的大小和变化规律均相同,主刚度系数、交叉刚度系数的绝对值均随转速的升高而增大,当转速从1 000 r/min升到5 000 r/min时,主刚度系数、交叉刚度系数的绝对值均为原来的5倍;主阻尼系数Cxx与Cyy的大小及变化规律也相同, 主阻尼系数、 交叉阻尼系数的绝对值随转速的升高而减小,但减小的程度并不大,当转速从1 000 r/min升到5 000 r/min时,主阻尼系数和交叉阻尼系数的绝对值分别减小了约0.19%和0.23%,转速小于3 000 r/min时,各阻尼系数随转速的增加而减小的趋势较明显,转速大于3 000 r/min后,可近似认为阻尼系数不再随转速的变化而变化。

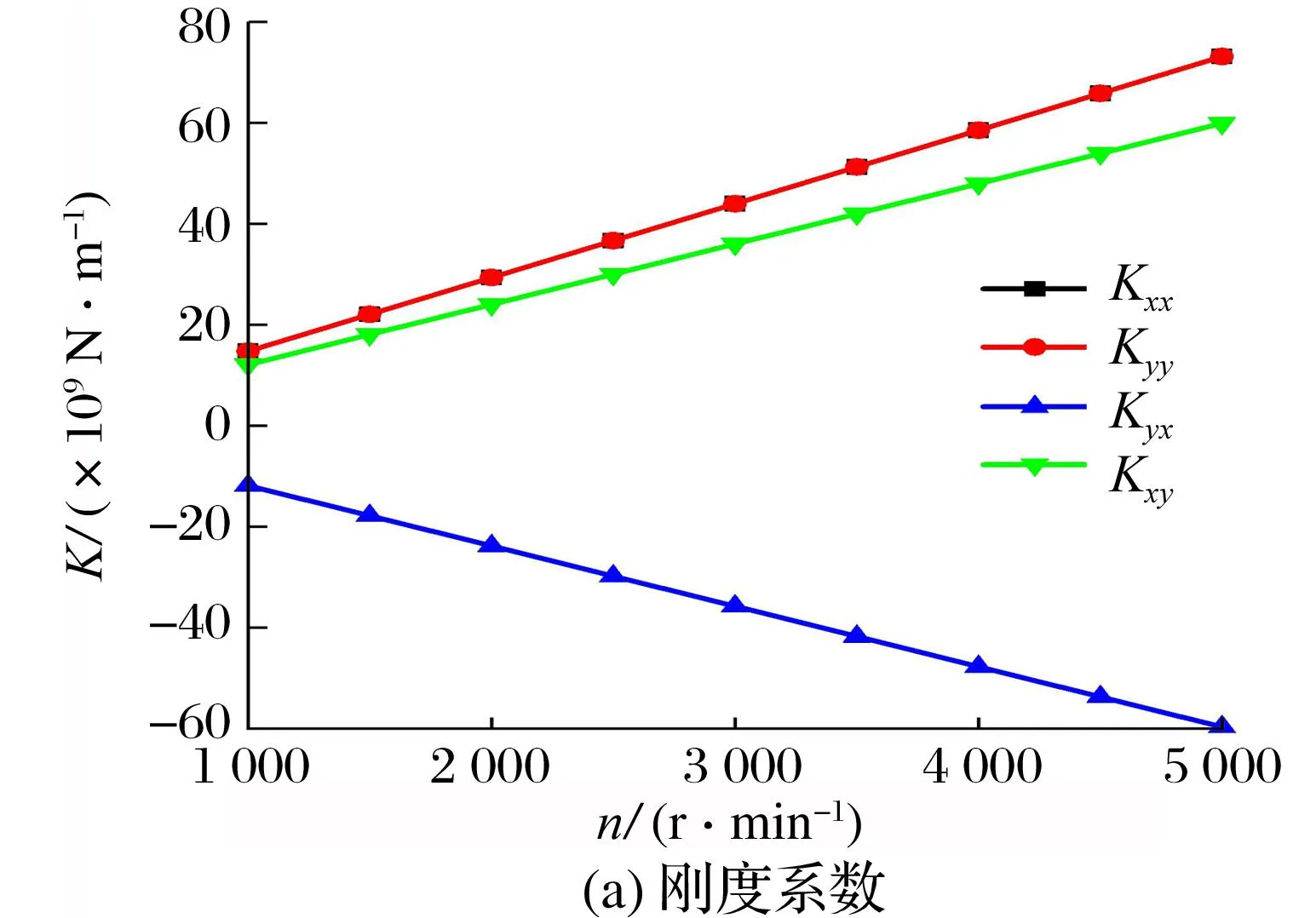
图7 转速对轴颈刚度系数和阻尼系数的影响

转速对瓦块角刚度系数和角阻尼系数的影响如图8所示:各瓦块的角刚度系数随转速的升高而增大,当转速从1 000 r/min升到5 000 r/min时,角刚度系数为原来的4.7倍;承载瓦的角阻尼系数随转速的升高而减小,当转速从1 000 r/min升到5 000 r/min时,角阻尼系数为原来的95.4%,非承载瓦的角阻尼系数随转速的升高而增大,当转速从1 000 r/min升到5 000 r/min时,角阻尼系数为原来的1.05倍。

3.3 瓦包角的影响

瓦包角对轴颈刚度系数和阻尼系数的影响如图9所示:主刚度系数Kxx与Kyy的大小相同,且随着瓦包角的增加而增大;交叉刚度系数大小相同,符号相反,绝对值随瓦包角的增加而增大;各阻尼系数的变化规律与刚度系数的相同;当瓦包角从45°增到85°时,主刚度系数和交叉刚度系数的绝对值分别为原来的3.7倍和3.8倍,主阻尼系数和交叉阻尼系数的绝对值分别为原来的4倍和35倍。增大瓦包角可以成倍地提高轴承刚度系数和阻尼系数的绝对值,从而极大改善了可倾瓦轴承的稳定性,提高轴承转子系统的抗振能力。

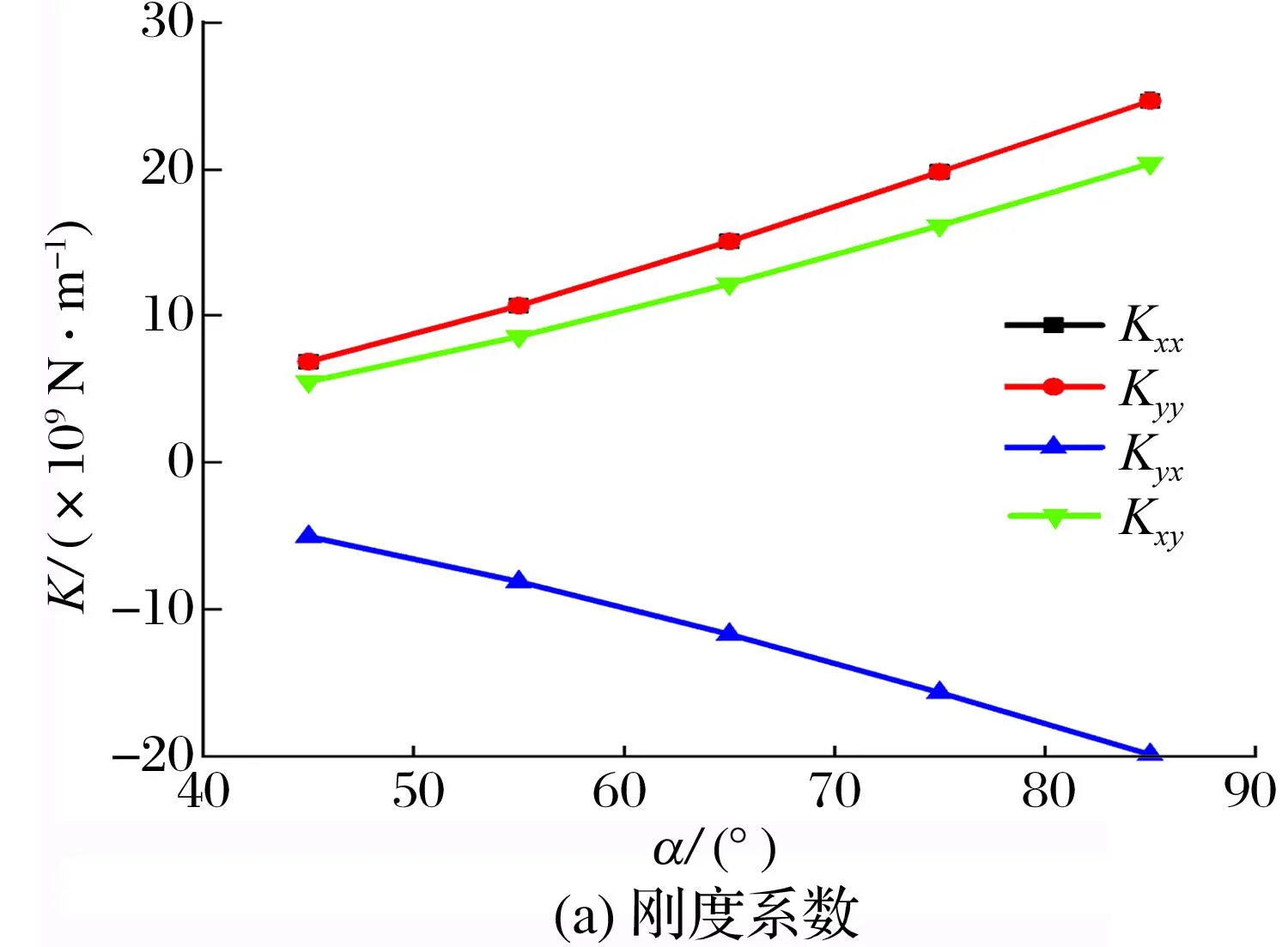
图9 瓦包角对轴颈刚度系数和阻尼系数的影响

瓦包角对瓦块角刚度系数和角阻尼系数的影响如图10所示:1#瓦与2#瓦的角刚度系数、角阻尼系数大小均相同,3#瓦与4#瓦的角刚度系数、角阻尼系数大小也相同,均随着瓦包角的增大而增大,承载瓦的角刚度系数和角阻尼系数比非承载瓦的略大,这是因为实际工作中承载瓦的服役预载荷会因偏心率的存在而小于设计预载荷,非承载瓦的服役预载荷会大于设计预载荷;当瓦包角从45°增到85°时,角刚度系数和角阻尼系数分别为原来的11倍和15倍。因此,增大瓦包角可以提高瓦块稳定性,预防因瓦块失稳导致的轴承故障。

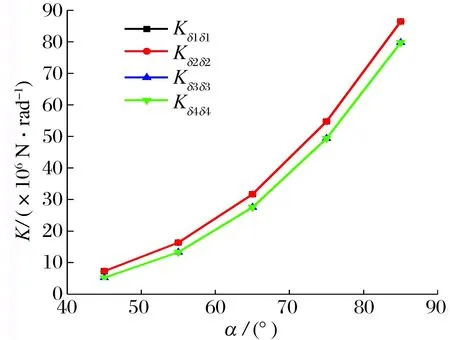
(a) 角刚度系数

3.4 间隙比的影响

间隙比对轴颈刚度系数和阻尼系数的影响如图11所示:主刚度系数Kxx与Kyy、主阻尼系数Cxx与Cyy的大小和变化规律相同,交叉刚度系数Kxy与Kyx、交叉阻尼系数Cxy与Cyx大小相同,符号相反;刚度系数、交叉阻尼系数的绝对值均随间隙比的增大而显著减小,当间隙比从0.06%增到0.3%时,主刚度系数、交叉刚度系数绝对值为原来的1.1%,主阻尼系数和交叉阻尼系数绝对值分别为原来的1.2%和0.2%。

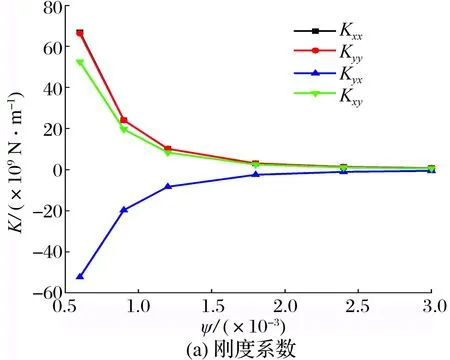
图11 间隙比对轴颈刚度系数和阻尼系数的影响

间隙比对瓦块角刚度系数和角阻尼系数的影响如图12所示:1#瓦与2#瓦的角刚度系数、角阻尼系数大小均相同,且随着间隙比的增大而减小,当间隙比从0.06%增到0.3%时,角刚度系数、角阻尼系数分别为原来的1.2%和1.4%;3#瓦与4#瓦的角刚度系数和角阻尼系数大小均相同,且随着间隙比的增大而减小,当间隙比从0.06%增到0.3%时,角刚度系数和角阻尼系数分别为原来的1.1%和0.7%。

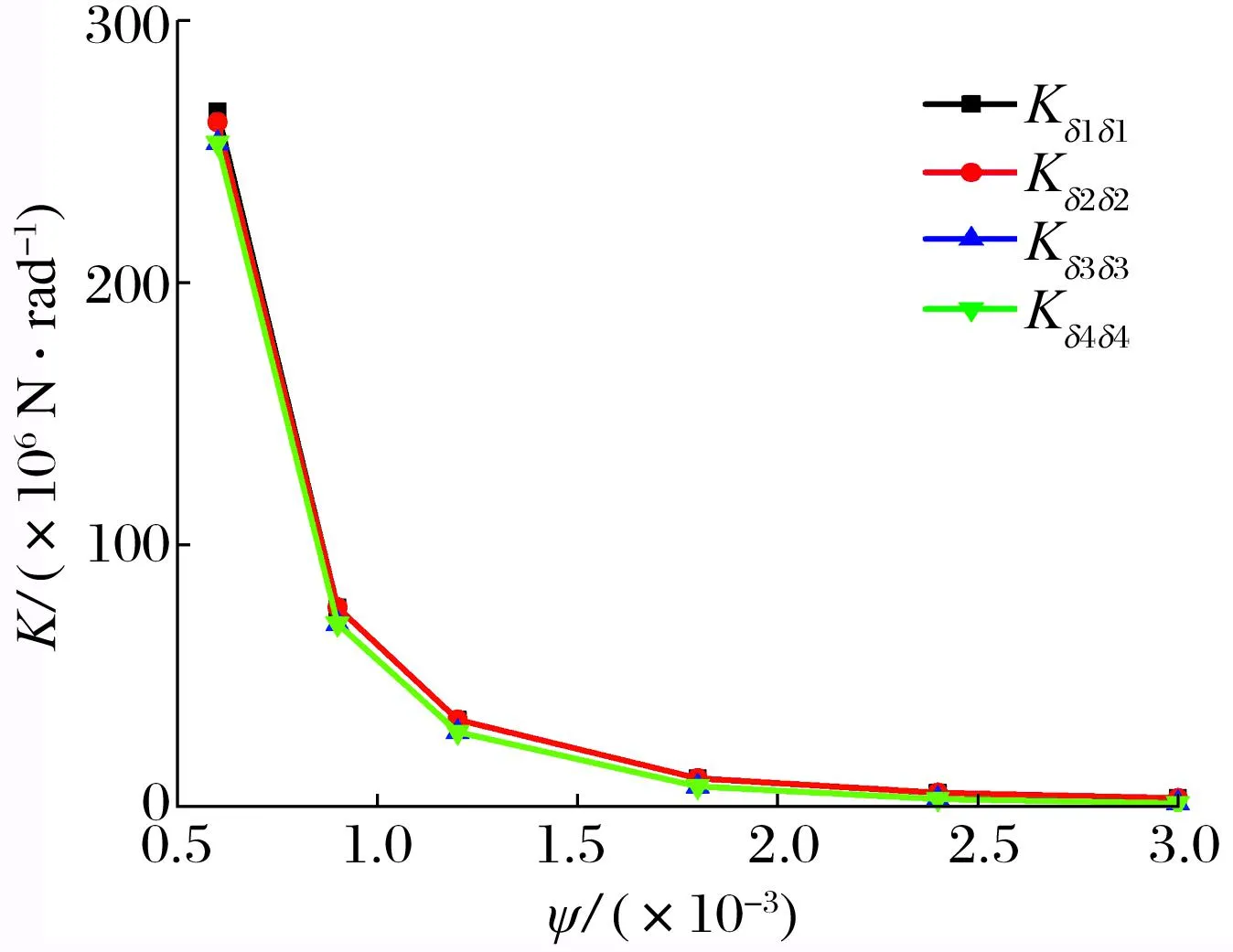
(a) 角刚度系数

综上可知,间隙比对可倾瓦轴承动特性系数的影响较大,轴承的各动特性系数随间隙比的增大呈指数式减小。间隙比主要影响轴承的半径间隙,因此减小轴承的半径间隙可显著提高轴承的工作稳定性。

3.5 预载荷系数的影响

预载荷系数对轴颈刚度系数和阻尼系数的影响如图13所示:主刚度系数Kxx与Kyy、主阻尼系数Cxx与Cyy的大小和变化规律相同,交叉刚度系数Kxy与Kyx、交叉阻尼系数Cxy与Cyx的大小相同,符号相反;当预载荷系数从0.4增到0.7时,主刚度系数为原来的8.6倍,交叉刚度系数的绝对值为原来的4.3倍;当预载荷系数从0.4增到0.8时,主阻尼系数为原来的4.6倍,交叉阻尼系数的绝对值为原来的13倍。因此,增加预载荷系数可以提高轴承稳定性。

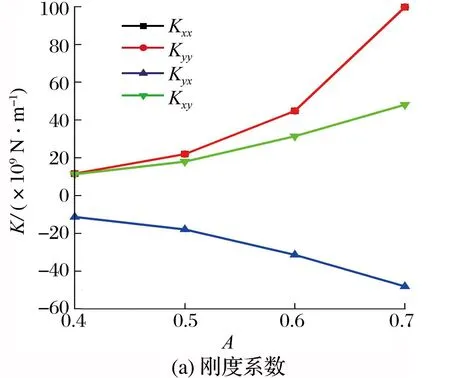
图13 预载荷系数对轴颈刚度系数和阻尼系数的影响

预载荷系数对瓦块角刚度系数和角阻尼系数的影响如图14所示:1#瓦与2#瓦的角刚度系数、角阻尼系数大小相同,3#瓦与4#瓦的角刚度系数、角阻尼系数大小也相同, 均随着预载荷系数的增加而明显增大;当预载荷系数从0.4增到0.8时,各瓦块角刚度系数为原来的9.7倍;当预载荷系数从0.4增到0.8时,1#瓦与2#瓦的角阻尼系数为原来的6.5倍,3#瓦与4#瓦的角阻尼系数为原来的7.3倍。因此,对瓦块施加一定的预载荷,减小各瓦的工作间隙可以提高瓦块稳定性,增强各瓦的抗冲击振动能力,但预载荷系数取值过大会带来安装、散热等问题,设计时应综合考虑各因素影响。

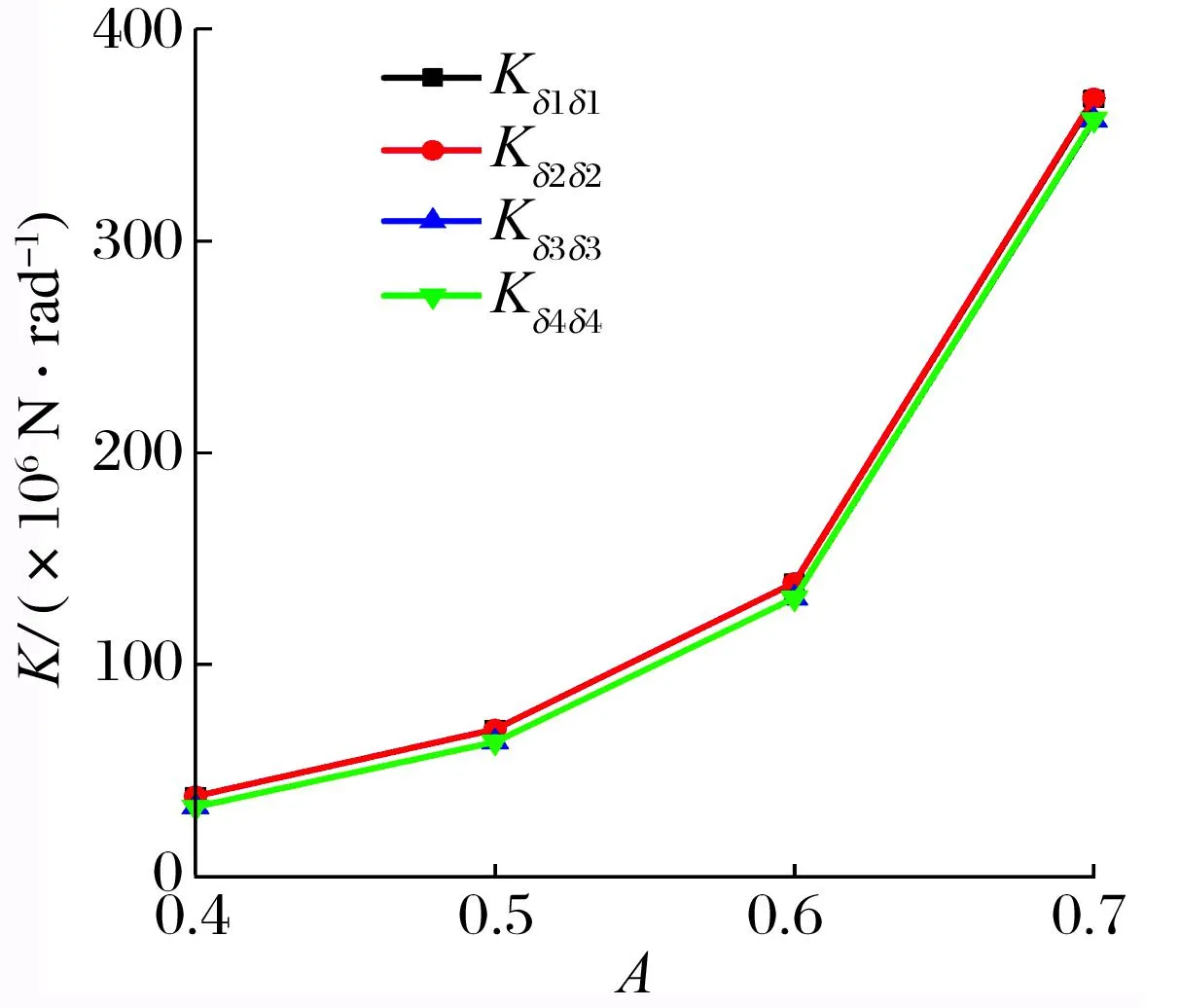
(a) 角刚度系数

预载荷系数对轴承工作间隙的影响较大,增大预载荷系数会成倍地增大轴承的动特性系数,说明轴承间隙对可倾瓦轴承动态性能的影响较大,而轴承间隙是预载荷系数、间隙比等参数综合作用决定的。因此,轴承转子系统的设计会涉及到多参数的优化。

3.6 支点系数的影响

在本文计算参数下,瓦块支点系数大于0.78时无法形成收敛油楔,而小于0.50时瓦块容易出现失稳故障,故选取支点系数为0.50～0.78。支点系数对轴颈刚度系数和阻尼系数的影响如图15所示:主刚度系数随支点系数的增加而增大,交叉刚度系数的绝对值随支点系数的增加而减小,支点系数由0.50增加到0.78时,主刚度系数为原来的3.3倍,交叉刚度系数的绝对值为原来的23%;主阻尼系数随支点系数的增加而减小,交叉阻尼系数的绝对值随支点系数的增加而增大,在支点系数从0.50增到0.78时,主阻尼系数为原来的40%,交叉阻尼系数的绝对值为原来的3倍。可见,增加支点系数会增大轴承主刚度系数且减小主阻尼系数,但主刚度系数的增加程度大于主阻尼系数的减小程度,设计时可根据对刚度系数和阻尼系数的实际需求合理选定支点系数。

图15 支点系数对轴颈刚度系数和阻尼系数的影响

支点系数对瓦块角刚度系数和角阻尼系数的影响如图16所示:各瓦块的角刚度系数均随支点系数的增加呈先增大后减小的趋势,承载瓦的角刚度系数和角阻尼系数比非承载瓦的大,且随着支点系数的增加两者之间的差值越来越小,在0.66～0.70之间存在一个支点系数使各瓦块角刚度系数最大,设计时可考虑采用此值使瓦块稳定性最高;角阻尼系数均随支点系数的增加而减小,当支点系数从0.50增到0.78时,1#瓦和2#瓦的角阻尼系数为原来的31%,3#瓦和4#瓦的角阻尼系数为原来的33%。因此大支点系数下瓦块的角刚度系数和角阻尼系数都较小,可倾瓦轴承的设计不宜选用太大的支点系数。

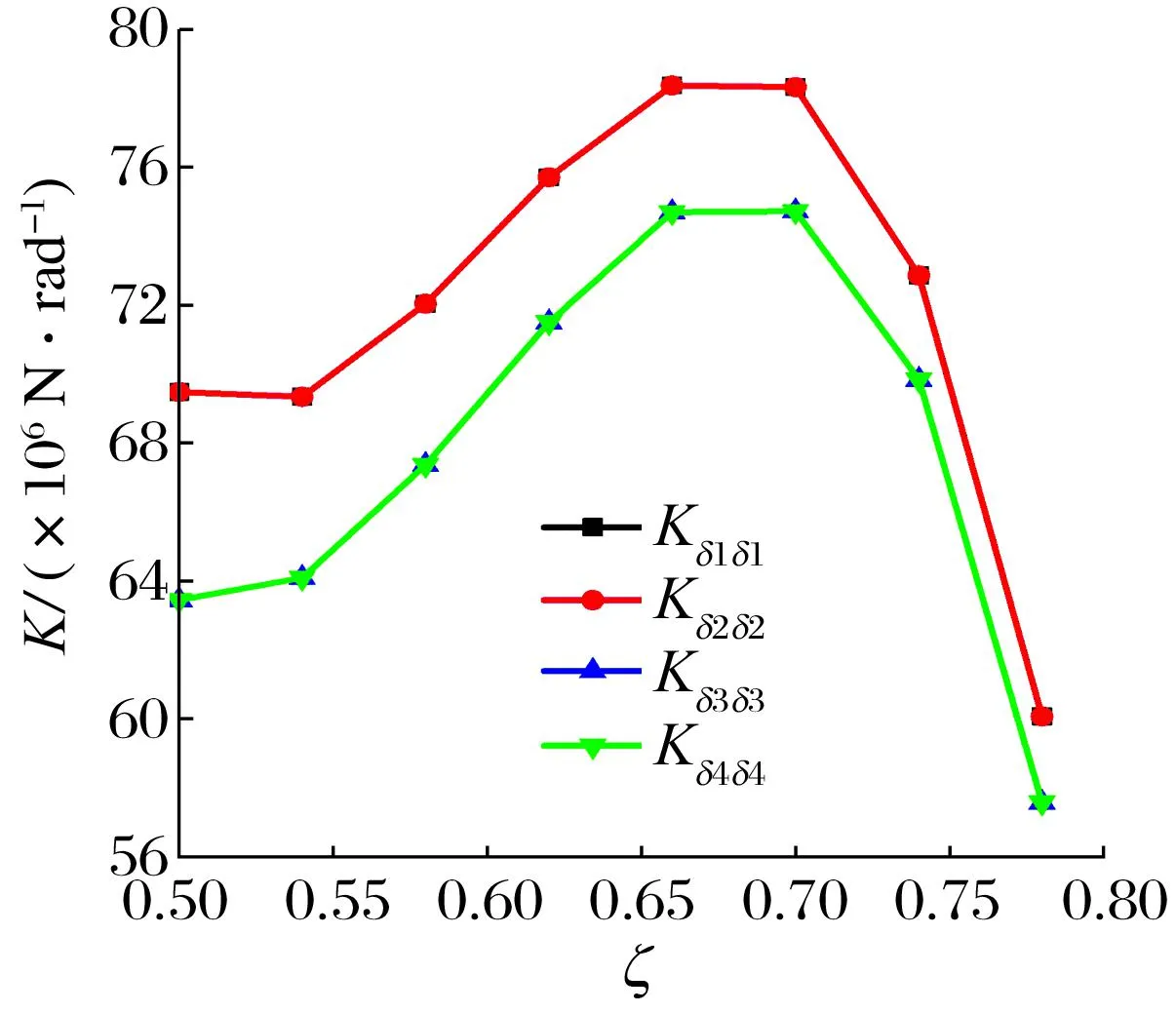
(a) 角刚度系数

3.7 长径比的影响

长径比对轴颈刚度系数和阻尼系数的影响如图17所示:刚度系数、阻尼系数的绝对值均随长径比的增加而增大,当长径比从0.3增到1.7时,主刚度系数为原来的16.39倍,交叉刚度系数的绝对值为原来的20.15倍,主阻尼系数为原来的21.37倍,交叉阻尼系数的绝对值为原来的9.25倍。

图17 长径比对轴颈刚度系数和阻尼系数的影响

长径比对瓦块角刚度系数和角阻尼系数的影响如图18所示:各瓦块的角刚度系数和角阻尼系数均随长径比的增加而增大;当长径比从0.3增到1.7时,1#瓦和2#瓦的角刚度系数为原来的9.52倍,3#瓦和4#瓦的角刚度系数为原来的21.07倍,1#瓦和2#瓦的角阻尼系数为原来的8.96倍,3#瓦和4#瓦的角阻尼系数为原来的18.05倍。因此,增加长径比可以提高各瓦块的稳定性,且对非承载瓦稳定性的提高效果更明显。

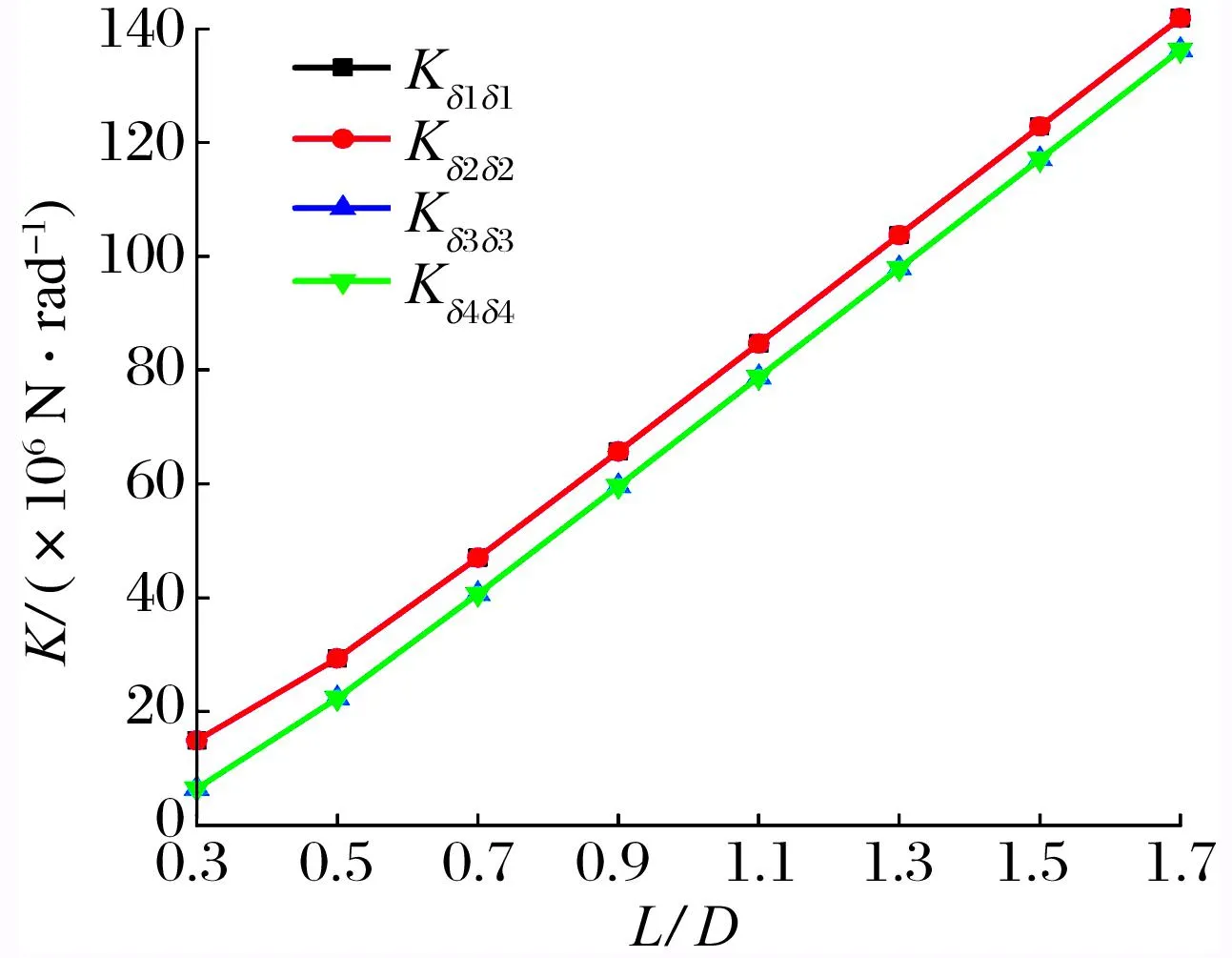
(a) 角刚度系数

综上可知,增加长径比可以显著提高轴承的动特性系数,尤其是对非承载瓦的稳定性提高效果明显,设计时可以考虑采用较大的长径比以避免非承载瓦失稳并改善轴承的使用性能,提高轴系稳定性,但长径比太大时轴颈会不可避免地产生挠度, 从而给轴承的使用及安装带来负面影响。

4 结论

以瓦间承载的四瓦可倾瓦轴承为研究对象,建立了考虑瓦块子结构的可倾瓦轴承广义完整动特性系数表征方法,研究了不同设计参数对动特性系数的影响规律,得到以下结论:

1)在不同计算参数下承载瓦的角刚度系数和角阻尼系数均比非承载瓦的大,说明承载瓦的稳定性优于非承载瓦。

2)对于轴颈动特性系数而言,存在一个载荷临界值,当载荷低于此值时,轴颈的动特性系数对载荷变化不敏感,当载荷大于此值时,轴颈的动特性系数随载荷的增加而显著增大;随着载荷的增加,承载瓦的动特性系数明显增大,非承载瓦的动特性系数明显减小,说明重载工况下非承载瓦易发生失稳故障。

3)升高轴承转速可提高轴承的各刚度系数、各瓦块的角刚度系数以及非承载瓦的角阻尼系数,但会降低轴承的各阻尼系数和承载瓦的角阻尼系数,说明过高的转速会降低转子轴承系统的减振能力。

4)增大长径比、预载荷系数和瓦包角,减小间隙比可以提高轴承的刚度系数和阻尼系数以及各瓦块的角刚度系数和角阻尼系数,在可倾瓦轴承的设计参数中,轴承间隙对动特性系数的影响最显著。

5)增大支点系数会使轴承的主刚度系数和交叉阻尼系数增大,同时使主阻尼系数、交叉刚度系数以及各瓦块角阻尼系数减小。各瓦块的角刚度系数随支点系数的增大呈先增大后减小的趋势,说明存在一个支点系数使各瓦块角刚度系数最大,设计时可考虑采用此值使瓦块稳定性最高。