高应力状态下两河口堆石料蠕变特性试验研究
孙向军,刘立强,邓韶辉,左永振,潘家军
(1.长江科学院 水利部岩土力学与工程重点实验室,武汉 430010; 2.雅砻江流域水电开发有限公司,成都 610065)
0 引 言
国家“十四五”规划和2035年远景目标建议中明确提出“实施雅鲁藏布江下游水电开发”[1],这表明未来我国土石坝的建设规模和难度越来越大。根据若干土石坝的运行观测结果,坝体在建成蓄水后,其变形持续发展,这种变形往往长达数十年[2],以正常蓄水位高程 400 m的水布垭面板堆石坝为例[3]:2007年集中蓄水完成后,库水位在355.68~399.51 m之间变化,2011—2015年的监测数据表明,个别测点的年沉降增量仍>10 mm。因此,研究筑坝堆石料蠕变特性是300 m级高土石坝关键性问题之一。
目前,关于筑坝堆石料的蠕变特性研究仍以室内三轴蠕变试验为主。基于试验结果,诸多学者提出了众多迥然不同的蠕变模型,如南科院六参数蠕变模型(李国英等[4],2004)、程展林九参数蠕变模型(程展林等[5], 2004)、增量蠕变模型(朱晟等[6], 2011)、弹黏塑性模型(王占军等[7],2014)、基于颗粒延迟破坏强度公式的蠕变模型(王峰[8], 2018)、统一考虑加载变形与流变的粗粒土弹塑性本构模型(陈生水等[9], 2019)、考虑nonisotach特性的堆石料时间相关本构模型(洪隽天[10],2020)等。这些成果较好地反映了堆石料的蠕变特性,并在计算分析中得到了较好的运用。
由于三轴蠕变试验,直接测得的变形,包含瞬时弹塑性变形与蠕变变形两部分,因此在提取蠕变模型参数时,将不可避免地采用若干假设,如假定瞬时弹塑性变形与蠕变变形的分界点。现有文献的蠕变模型参数,大多未明确说明其采用的假设,导致同一组原始试验数据,无法唯一确定其模型参数。
程展林等[5]提出的九参数幂函数模型,因其引入剩余蠕变等物理量,在一定程度上,具备显著的优势。花俊杰等[11]、周伟等[12]采用长江科学院(以下简称长科院)九参数蠕变模型,对双江口心墙坝(坝高314 m)进行了简单的长期变形数值模拟;徐晗等[13]基于九参数蠕变模型,分析了砾质土心墙料蠕变特性对坝体应力变形的影响。但长科院九参数蠕变模型参数过多,且参数缺乏明确的物理含义。
对此,本文以两河口水电站的上游堆石料和下游堆石料为研究对象,开展高应力状态下的大型三轴蠕变试验。在试验结果分析基础之上,提出一种更为简化的蠕变模型,以便为大坝(竣)工后变形的初步估算提供依据。
1 试验材料及方案
1.1 试验材料
两河口水电站是我国目前在建的300 m级土石坝的代表性工程,其坝型为砾石土心墙堆石坝,最大坝高295 m。
试验材料取自于两河口水电站心墙坝筑坝料实际料场,一种取自于瓦支沟料场,主要填筑在上游堆石Ⅰ区,文中称为堆石料A;另一种取自于两河口料场,主要填筑在下游堆石Ⅰ区,称为堆石料B。
两种堆石料岩性均是板岩与砂岩混合料,区别在于板岩、砂岩含量略有差异,且均为新鲜料,在105~110 ℃温度下烘至恒重时的质量与同体积4 ℃时水的质量之比值为2.76。
1.2 试验级配和制样密度
为使试验成果更贴近工程实际,本次研究的原始级配,采用由坝体填筑高度80~220 m范围内,上游堆石Ⅰ区的157组检测级配及下游堆石Ⅰ区的267组检测级配所得的级配平均线。
根据《土工试验方法标准》(GB/T 50123—2019)[14]的缩尺方法,对原始级配采用混合法进行级配缩尺,得到本次试验级配,如图1所示。

图1 试验级配曲线
采用试验级配,进行堆石料的最大干密度试验,最大干密度试验采用表面振动法,试样筒尺寸Φ300 mm×H340 mm,试样分2层,每层振击8 min。
根据最大干密度试验成果,堆石料A的最大干密度2.25 g/cm3,堆石料B的最大干密度为2.26 g/cm3。室内试验采用2.20 g/cm3的试验干密度进行试验,对应的孔隙率为20.3%。
1.3 试验仪器及试验步骤
蠕变试验采用长江科学院 YLSZ30-3 型应力应变式高压三轴仪,试样直径Ф300 mm,最大围压3.0 MPa,最大轴向应力21 MPa,最大轴向行程300 mm。
该仪器的系统组成包括:竖向荷载加载、稳压、控制系统;周围压力加载、稳压、控制系统;三轴压力室;反力框架;位移、体变量测系统;荷载传感器及数据采集系统等。为了能提供蠕变试验需要的稳定轴向压力,该仪器另外配有专门稳压的高压蓄能罐。具体见图2。

图2 长江科学院 YLSZ30-3 型三轴试验仪
试验周围压力σ3为1.0、2.0、3.0 MPa共3种。试样填装均按4层进行,从底孔采用水头饱和方法对试样进行饱和。试验过程中记录轴向荷载、轴向位移、排水量等。
为得到峰值强度,首先开展饱和三轴CD试验,试样剪切至轴向应变的15%停止试验,由应力应变曲线峰值点得破坏剪应力。根据试验得到的最大剪应力值,按围压计算预施加的应力水平SL=0.2、0.4、0.6、0.8时的剪切应力竖向荷载,并分级施加在试样上。在已知应力条件下,稳定应力状态若干时间,记录不同时刻试样变形,当变形趋于稳定后施加下一级荷载。
为了避免温度变化对试验成果的影响,试验室采用空调进行温度控制,试验过程中温度控制在(20±1)℃左右。
2 试验结果
2.1 固结排水三轴剪切试验结果
图3给出了2种堆石料固结排水三轴剪切试验结果。

图3 固结排水三轴剪切试验结果
由轴向应变εa在15%以内对应的剪应力(σ1-σ3)的峰值强度(破坏剪应力)指标(σ1-σ3)f。
由此可得任意围压σ3、应力水平SL对应的平均正应力p及广义剪应力q:
(1)
由p、q值可得应力比η=q/p。
2.2 三轴蠕变试验结果
堆石料A三轴蠕变试验的轴向应变、体积应变结果如图4所示,堆石料B与之类似,本文从略。
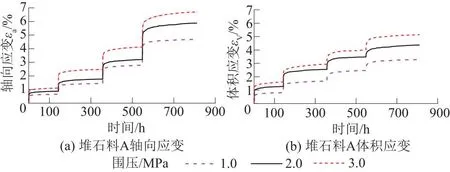
图4 堆石料A三轴蠕变试验结果
已有大量研究表明:当应力增量足够大时,粗粒料的蠕变过程只与应力状态有关,而与应力增量大小无关。
基于上述结论,由图4所示分级加载曲线可得各种应力状态对应的轴向应变εa、体积应变εv与时间的关系曲线。
堆石料A部分应力状态结果如图5所示,堆石料A其余应力状态及堆石料B结果与图5类似,本文从略。
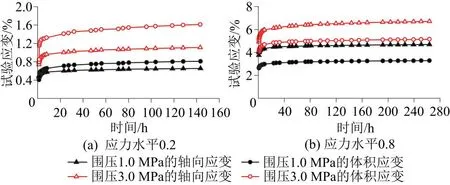
图5 堆石料A典型时程曲线
由图5可知,在低应力水平下, 轴向应变εa小于体积应变εv,侧向应变εr=(εv-εa)/2为正,即主要为围压产生的径缩现象;在高应力水平下, 轴向应变大于体积应变,侧向应变εr=(εv-εa)/2为负,即主要为轴压产生的径胀现象。
其余应力状态的试验结果亦呈现出了该规律, 李海芳等[15]的试验研究亦得到了相同规律。
鉴于图5所示应变值包含瞬时弹塑性应变与蠕变应变两部分,本文重点研究堆石料蠕变特性,对其不加详细分析。
3 蠕变模型及其参数
按照滞后变形理论,以图5为代表的三轴蠕变试验直接得到的总应变ε(t)可分为瞬时产生的弹塑性应变εep和滞后产生的蠕变应变(黏滞应变)εL(t)两部分。
长科院九参数蠕变模型引入了极限应变εm、剩余蠕变εo(t)、最终蠕变εf三类应变指标。各应变量之间满足式(2)关系,即
εo(t)=εf-εL(t)=εm-ε(t)=
εm-[εL(t)+εep] 。
(2)
瞬时产生的弹塑性应变εep可由邓肯-张等模型计算得到。
3.1 外推确定的极限应变
采用幂函数拟合试验结果,拟合如图6所示。

图6 试验幂函数外推拟合示意图
图6中剪切应变εs=εa-εv/3,由轴向应变及体积应变计算得来。
鉴于幂函数无上界,故以幂函数外推30 a的应变值作为极限应变εm。
记极限时间tm=30×365×24 h,则极限轴向应变εam、极限剪切应变εsm确定公式为
(3)
式中A、b、C、d均为参数。
长科院九参数蠕变模型亦采用该种方法外推确定极限应变值。采用该方法,可规避不同本构模型计算的εep不一致导致蠕变εL(t)不同,最终导致蠕变模型参数不唯一的现象。
关于式(3)中参数A、b、C、d,笔者发现与应力比η具有良好的对应关系,但其仅用以外推30 a时的试验值,故不必详细研究。
3.2 剩余蠕变拟合
由外推确定的极限应变值εm减去试验值ε(t),即得各时刻的剩余蠕变,采用幂函数拟合剩余蠕变t>1 h的时程曲线,典型拟合如图7所示。

图7 剩余蠕变拟合典型曲线
结合式(2)可得
(4)
式中:εaf、εsf分别为某个应力状态下最终轴向蠕变和最终剪切蠕变;εa0(t)、εs0(t)分别为t时刻的剩余轴向蠕变、剩余剪切蠕变;εaL(t)、εsL(t)分别为t时刻的轴向蠕变、剪切蠕变;λa和λs分别为轴向蠕变和剪切蠕变的衰减幂指数。
3.3 最终剪切蠕变模量及衰减幂指数
各种应力状态对应的衰减幂指数λa和λs如表1所示。

表1 2种堆石料的衰减幂指数
由表1可以看出,除去最大和最小值,参数λa和λs值基本在一个较小的范围内波动,平均值均为0.08。
以剪应力q=σ1-σ3为纵坐标,以最终剪切蠕变εsf为横坐标,绘制图8。

图8 最终剪切蠕变-剪应力关系曲线
由图8可知,最终剪切蠕变与剪应力之间满足正比关系,仿照剪切模量的物理含义,定义最终剪切蠕变模量Gf为
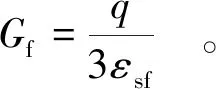
(5)
由图8可以看出,堆石料A最终剪切蠕变模量为118.8 MPa,堆石料B最终剪切蠕变模量为113.5 MPa。
以最终轴向蠕变εaf为纵坐标,以最终剪切蠕变εsf为横坐标,绘制图9。
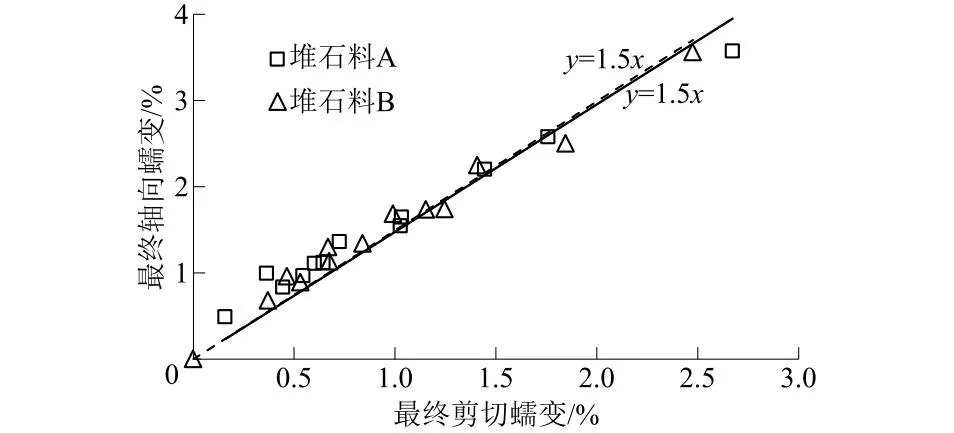
图9 最终剪切蠕变-最终轴向蠕变关系曲线
由图9可知,二者之间满足正比关系,且比例系数为1.5,即
(6)
3.4 两参数蠕变模型及其讨论
综合前述研究,由式(4)—式(6)推导可得,仅含两个参数的幂函数蠕变模型,即
(7)
式中:εsL(t)、εVL(t)分别为t时刻的剪切蠕变、体积蠕变;Gf为前文定义的最终剪切蠕变模量;λ为衰减幂指数。
式(7)所示的两参数幂函数蠕变模型的优点在于形式简洁,参数物理含义明确,易于在工程中使用。
式(7)所示的两参数幂函数蠕变模型不足之处在于拟合精度略有不足,加之重塑缩尺级配样的室内蠕变试验结果与实际筑坝料蠕变特性之间本身存在差异,故该模型仅可初步估算土石坝蠕变变形。
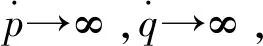
由式(7)求导可得蠕变变形速率为
(8)
在实际模拟过程中,可考虑采用相对时间取代绝对时间的策略,即
(9)
式中Δt为数值模拟时间步长。
目前,常采用Prandtl-Reuss流动法则,计算蠕变张量{εL}=εVL{I}/3+εsf{S}/q;其中{I}为单位张量,{S}为偏应力张量,q为广义剪应力;进而将蠕变模拟为“初应变”进行蠕变变形计算。
土石坝在竣工(填筑高度达预定坝高)后,坝体产生工后变形的复杂原因如下:
(1)水库蓄水后上游面的水压力及上游浸水部位铅直向上的浮托力作用。
(2)上游浸水部位的湿化变形作用。
(3)堆石料的时间蠕变特性。
(4)温度变化、干湿循环、风化等复杂环境条件下堆石料的劣化作用。
因此关于蠕变变形的详细数值模拟,必须结合堆石料劣化模型、湿化变形模型开展,本文暂不介绍两河口水电站砾石土心墙堆石坝工后变形数值模拟成果。
4 结 论
(1)2种筑坝堆石料室内三轴蠕变试验结果,在低应力水平下,侧向应变为正,即主要为围压产生的径缩现象;在高应力水平下,侧向应变为负,即主要为轴向加荷产生的径胀现象。
(2)与长江科学院九参数蠕变模型相同: 可以采用幂函数外推30 a时对应的试验值作为堆石料蠕变试验的极限应变; 剩余蠕变与时间呈良好的幂函数关系,进而得到了衰减幂指数以及最终蠕变。
(3)最终剪切蠕变与剪应力呈倍数关系,轴向蠕变衰减幂指数与剪切蠕变衰减幂指数基本相等,最终轴向蠕变是最终剪切蠕变的1.5倍。基于此规律,笔者提出了更为简化的两参数幂函数蠕变模型,并对该模型进行了简要的讨论。

