带运输的混合流水车间调度问题的改进遗传算法

许 可叶彩霞孙文娟

(1.沈阳理工大学a.理学院，b.自动化与电气工程学院，沈阳 110159；2.辽宁省兵器工业智能优化与控制重点实验室，沈阳 110159)

混合流水车间调度问题(hybrid flow shop scheduling problem，HFSP)将传统的流水车间和柔性生产线相结合，研究在具有多个设备、多种不同类型任务和各种约束条件的制造环境中如何合理安排工作任务和分配时间，以实现某种性能指标的优化。 HFSP 广泛存在于玻璃、纺织、造纸和钢铁等制造业领域[1]，该问题已被证明属于NPhard 问题[2]，其求解难度较大。 在分布式制造环境下，各工序的加工制造设备可能处于不同的地理位置，在考虑设备制造能力的同时，也要兼顾运输时间对调度结果的影响。 对企业来说，研究考虑运输时间的HFSP 具有重要的现实意义。

目前，许多学者开展了HFSP 研究。 轩华等[3]研究了带运输时间的多阶段动态可重入HFSP，目标函数为最小化总加权完成时间，设计了两种改进的拉格朗日松弛算法，提高了解的质量和运行时间。 袁帅鹏等[4]研究了带有序列相关准备时间和阶段间运输时间的混合流水车间成组调度问题，以最小化最大完工时间为目标，设计了一种协同进化文化基因算法，并通过对比实验证明了算法的有效性。 耿凯峰等[5]研究了带工序跳跃的绿色混合流水车间机器和自动引导车联合调度问题，提出了改进的文化基因算法，实现了最大完工时间和总能耗同时最小化。 Hidri 等[6]研究了带有转移时间和运输时间的两阶段HFSP，以最小化最大完工时间为优化目标，提出了一种由两阶段组成的启发式方法，该方法能够在可接受的计算时间内提供最优解或近似最优解。 Li 等[7]针对混合流水车间生产运输一体化调度问题，设计了一种有效的遗传禁忌搜索算法，达到了最大完工时间的最小化。 Yuan 等[8]研究了考虑阻塞和运输时间的二机流水车间成组调度问题，设计了协同进化遗传算法，实现了最小化最大完工时间。上述研究均属于将运输和生产协同考虑的并行同速机的HFSP，而在不相关并行机的HFSP 方面研究则较少，且目前的求解方法也多为智能优化算法和精确算法，求解质量和求解效率都不高，易陷入局部最优。

近年来，随着机器学习的快速发展，将强化学习(reinforcement learning，RL)与智能优化算法相结合用于解决相关领域的调度问题受到广泛关注。 尹爱军等[9]研究了柔性作业车间多目标优化调度问题，针对算法多样性不足、易于早熟及局部收敛的缺点，提出了一种基于RL 的改进非支配排序遗传算法。 张韵等[10]提出了一种基于机器学习的多策略并行遗传算法，通过引入能自主感知环境的RL，实现遗传算法(GA)中重要参数交叉概率的自学习。 李润佛等[11]为解决港口拥堵问题，提出了一种基于RL 的自学习遗传算法(SLGA)，减少了船舶在港等待时间，提高了港口通航效率。 Shahrabi 等[12]针对考虑随机作业到达和机器故障的动态作业车间调度问题，使用Qlearning 算法来提高可变邻域搜索(VNS)算法的性能。 Cao 等[13]针对柔性作业车间调度问题，通过RL 算法构建了布谷鸟搜索算法的自适应参数控制方案，提出了一种基于知识的布谷鸟搜索算法。 Alipour 等[14]将GA 和RL 相结合，用于求解旅行商问题(TSP)，取得了较优的结果。 Chen等[15]针对柔性作业车间调度问题，将GA 作为基本优化方法，采用RL 对其关键参数进行智能调整。 上述研究中将机器学习与智能优化算法相结合，提高了算法求解性能及求解质量。

带运输的HFSP 是一个复杂的组合优化问题，需要综合考虑加工时间、运输时间和优先级约束，以实现最优的调度方案。 GA 稳定性好、通用性强，是求解HFSP 最常用的算法。 GA 中交叉概率和变异概率的设置直接影响算法的搜索能力和收敛速度，针对不同的调度问题，交叉概率和变异概率等参数通常采用实验分析[16]或经验来确定。目前，在HFSP 的求解中，关于GA 参数智能调整的研究很少。 本文以最小化最大完工时间为目标，建立带运输的HFSP 优化模型，提出一种基于Q-learning 的改进遗传算法(QGA)求解该模型，采用Q-learning 算法智能调整GA 的交叉概率和变异概率，提高算法的求解效率和求解质量。

1 带运输的HFSP 模型

现有n个工件需要在L道工序上进行加工，工件序号为j(j＝1，2，…，n)，工序序号为l(l＝1，2，…，L)，第l道工序中有ml台不相关并行机器，机器序号为k(k＝1，2，…，ml)，全部工序共有M台机器，各机器位于不同地点。 混合流水车间调度流程如图1 所示。

图1 车间调度流程图Fig.1 Flow chart of shop scheduling

为简化模型，进行如下假设:

1)工序间缓冲区的容量无限；

2)相邻工序间存在运输阶段，且不受运输工具的制约；

3)工件一旦开始加工或运输，不可中断；

4)所有工件在零时刻已经到达并可以开始加工。

为实现最大完工时间最小化，需要决策每个工件在每道工序的生产机器以及各工件在该机器上的生产顺序。

为准确描述HFSP，定义如下参数和决策变量:bj，l表示工件j在工序l的开始加工时间；ej，l表示工件j在工序l的加工完成时间；表示工件j在工序l的机器k上的加工时间；表示工件从当前工序的机器k运输到下一道工序的机器k′的时间；表示决策变量，若工件j在工序l选择机器k加工，为1，否则为0；σ表示一个可行的整体调度方案；Cmax表示所有工件的最大完工时间。

基于上述说明，建立如下数学模型。

模型各方程中:式(1)表示目标函数；式(2)表示工件的加工时间；式(3)表示工件的运输时间；式(4)表示工件在机器前等待加工时间；式(5)表示工件在每道工序的完工时间必须大于其相应工序的开始加工时间，且所有工件开始时间不为负；式(6)表示工件在前一道工序完工之后需经过运输方能在下一道工序开始加工；式(7)表示每道工序中一个工件只能选择一台机器加工；式(8)表示工件完工时间等于工件开始时间与其加工时间之和。

2 基于Q-learning 的改进遗传算法

传统GA 中交叉概率(Pc)和变异概率(Pm)等参数需要依靠实验分析或经验确定，参数数值过大时，会使求解速度过慢，不易寻得最优解，数值过小时，很难产生新的个体。 针对该问题，本文采用Q-learning 算法对参数进行智能化调整，根据种群当前状态和过去状态智能选择Pc和Pm，并对未来状态进行预测，从而提高求解效率和精度。

2.1 编码与解码

在第一道工序上采用基于工件序号的编码方式表示工件的加工优先级，在其余工序上采取先来先服务的原则。 每条染色体包含n个基因位，分别对应n个工件的序号。 解码基于最早完工时间解码算法，计算工件在某道工序所有加工机器上的完工时间，选择完工时间最少的机器进行加工。

编码与解码过程示例如下。

设有三个工件依次经过2 道工序进行加工，共有4 台加工机器，每道工序的机器数量均为2台。 各工件在机器上的加工时间分别为:机器间的运输时间分别为:。 如果染色体编码为[3 1 2]，解码结果如图2 所示，图中二元组表示工件序号与工序序号。

图2 解码结果示意图Fig.2 Diagram of the decoding result

2.2 适应度函数和遗传操作

适应度函数在GA 中起着关键作用，其值越高，个体就越接近最优解，反之，则个体越差。 适应度函数计算式为

采用转盘赌选择、部分匹配交叉和两点交换变异的方法对染色体进行选择、交叉和变异操作。

2.3 Q-learning 算法

Q-learning 是一种经典的RL 算法，属于基于价值函数的方法。 在使用Q-learning 算法求解问题时需要考虑状态、行动、报酬和策略四个要素，Q值更新计算中需综合考虑智能体过去所经历的状态、动作和奖励，公式为

式中:Q(st，at)表示在状态st采取行动at时的Q值；rt为即时奖励；α为学习率；maxQ(st＋1，at＋1)表示在状态st＋1时采取行动at＋1得到Q值表中期望最高的Q值；γ为折扣率。

2.3.1 状态特征

GA 中判断种群好坏的指标通常包括平均适应度、多样性及最佳个体适应度。 平均适应度反映了种群整体的适应能力；多样性反映了种群内个体之间的差异；最佳个体适应度反映了种群中最优个体的适应性水平。 平均适应度越高、多样性越高、最佳个体适应度越高，说明种群的适应能力越强。 因此，为更好地评价种群的表现，选择种群的平均适应度、多样性以及最佳个体适应度作为种群的状态集合。

设种群在第t代的平均适应度为Ft、第t代种群的多样性为Dt、种群在第t代最佳个体适应度为Mt、种群状态值为S∗，计算方法如式(11) ~(14)所示。

式中:N为种群中个体数量；w1、w2、w3分别表示三个指标的权重，w1＋w2＋w3＝1。 本文采用种群的平均适应度和多样性反映种群的整体状态，有利于获得更优秀的个体，因此w1和w2值比w3值相对重要，取w1＝0.35、w2＝0.35、w3＝0.3。

状态的划分对收敛性影响很大:划分过多，寻优耗时较长；划分过少，确定的方案较差。 为此，基于GA 求解HFSP 的适应度和S∗值时，划分为10 个状态，状态向量表示为S＝[s(1)，s(2)，…，s(10)]，S∗的间隔为0.1。 如状态为s(1)，S∗∈[0，0.1)；如状态为s(2)，S∗∈[0.1，0.2)。 依此类推。

2.3.2 动作

每一代智能体都会选择不同的动作得到合适的Pc和Pm，其中Pc的取值范围为0.4 ~0.9，动作间隔为0.1，动作集中包含10 个动作。 如动作设为a1时，Pc∈[0.4，0.5)，则Pc从该区间内随机选择一个值；动作设为a2时，Pc∈[0.5，0.6)。Pm的选择与上述类似，取值范围为0.01 ~0.21，间隔为0.04。 如动作设为a1时，Pm∈[0.01，0.05)，则Pm从该区间内随机选择一个值。

2.3.3 奖励

奖励通过最佳个体适应度和种群平均适应度来设计。 调整Pc后的奖励rc与调整Pm后的奖励rm计算见式(15)与式(16)。

2.3.4 探索与利用

ε－贪心策略是一种同时考虑探索和开发的行动选择策略，即以概率ε随机选择一个动作，以概率1－ε选择Q值最大的动作，表达式为

式中:A(s)表示状态为s时选择的动作；P为选取动作的概率。

2.4 算法流程

将Q-learning 与GA 结合，设计如图3 所示的QGA 框架，包括环境、学习模块和强化过程三部分。

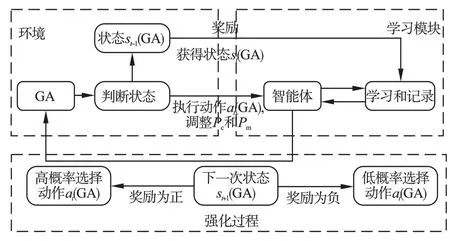
图3 QGA 框架Fig.3 Framework of QGA

采用基于Q-learning 算法设计的QGA 求解考虑运输时间的HFSP，具体步骤如下。

步骤1初始化参数，包括调度问题参数、GA参数、Q-learning 算法参数。

步骤2初始化Q值表，包括状态集、动作集、策略。

步骤3随机生成初始种群，设置当前迭代次数t＝0。

步骤4计算当前个体的适应度值，并采用轮盘赌方法对父代染色体进行选择。

步骤5获取所有个体在第t次迭代时的状态st，使用ε－贪心策略根据Q值表选取动作，获得调整后的Pc和Pm。

步骤6计算从状态st采取行动at到状态st＋1所获得的奖励r(st，at，st＋1)，并根据式(14)更新Q值表。

步骤7使用更新后的参数进行交叉和变异操作，生成新的个体。

步骤8判断是否达到最大迭代次数，如果是，输出结果，结束计算，否则令t＝t＋1，转到步骤4。

3 仿真实验与分析

采用仿真实验验证本文算法的有效性。 实验硬件环境为:Intel(R)Core(TM)i5-7200U CPU 2.50 GHz、20 G 内存。 采用PyCharm2017.3.2 编译器、python3.7 解释器软件编程实现。

3.1 初始条件与参数选择

在仿真实验中，取工件数量n＝40，工序数量L＝3，每道工序的机器数量分别为m1＝3、m2＝2、m3＝4。 工件在每台机器上的加工时间在1 ~8之间随机生成，各机器间的运输时间在1 ~5 之间随机生成。

采用不同参数进行仿真计算，通过比较目标函数值确定GA 的最佳参数取值。 计算结果如表1所示。

表1 不同GA 初始参数下的仿真计算结果Table 1 Simulation results with different GA initial parameters

由表1 可见，目标函数值Cmax最小为73，据此选取种群规模为130、交叉概率为0.7、变异概率为0.01。 变异概率过高会使算法近似于随机搜索，难以得到最优解，种群数量过小会使算法陷入局部最优。

为确定Q-learning 算法的参数取值，采用不同参数进行仿真计算，结果如表2 所示。

表2 不同Q-learning 算法初始参数下的仿真计算结果Table 2 Simulation results with different initial parameters of Q-learning algorithm

由表2 可见，目标函数值Cmax最小为72，据此选择学习率为0.01、折扣率为0.95、贪婪率为0.3。学习率越低，保留之前的学习经验越多，越容易得到最优解；折扣率越高，越重视以前的经验，越容易得到最优解；贪婪率居中选取为优。

图4 为上述最佳实验参数下算法迭代到400代时目标函数值的收敛情况。 由图4 可见，在迭代次数为150 时，Cmax值已经趋于稳定，故本次实验最大迭代次数选择为150。

图4 Cmax的迭代收敛图Fig.4 The iterative convergence plot of Cmax

3.2 实验结果分析

为验证本文QGA 的可行性，在两组不同生产规模(工件、工序及机器数量各不相同)下进行实验。 实验设置如表3 所示，表4 为不同生产规模下重复进行10 次实验得到的最优Cmax值。

表3 实验设置Table 3 Experimental setup

表4 不同生产规模下的实验结果Table 4 Experimental results under different sizes

由表4 可知，在不同规模下达到最优值的概率均为90%，证明了本文算法的稳定性。 图5 和图6为对应两种规模下的最优调度甘特图，可以看到，机器的空闲时间较少，说明机器的利用率高，能够获得较小的最大完工时间，验证了本文QGA 算法的可靠性。

图5 n ＝12 和L ＝4 的调度甘特图Fig.5 Schedule Gantt chart with n ＝12 and L ＝4

图6 n ＝9 和L ＝8 的调度甘特图Fig.6 Schedule Gantt chart with n ＝9 and L ＝8

图7和图8 分别为不同平均适应度下Pc和Pm的变化情况。 由图7 可以看到，随着平均适应度的增加，Pc增大，说明平均适应度高时，种群中包含一些较优秀的个体。 为保留优秀基因，选择较高的Pc，以在交叉操作中更频繁地将优秀个体的基因信息进行传递。 由图8 可见，随着平均适应度的增加，Pm降低。 这是因为此时种群已经优化，通过适当降低Pm，防止种群过早收敛到局部最优解。

图7 Pc 的取值变化图Fig.7 The graph of the value change of Pc

图8 Pm 的取值变化图Fig.8 The graph of the value change of Pm

3.3 实验对比

为验证本文算法的优势，在不同生产规模下，采用基于禁忌搜索改进的遗传算法(GA-TS)和QGA 进行实验对比分析。 规模参数为:n取10、25、50、100；L取3、5、8；M取9、10、13，机器随机分布在每道工序。 当n＜50 时视为小规模，否则视为大规模，表5 和表6 分别为小规模和大规模下的对比结果。 表中:T1为迭代1 次所需要的时间；Toptimal为首次达到最优结果所需的时间。 为避免实验误差，每组实验重复5 次取平均值。

表5 小规模下的实验结果对比Table 5 Comparison of experimental results at a small scale

由表5 和表6 可知，在24 个测试实例中，QGA在20 个实例中的Cmax值都优于GA-TS，另外4 个实例求得的Cmax值相同。 求解小规模问题时，GATS 的Cmax平均值为75，本文QGA 的Cmax平均值为73，减少了2.7%；求解大规模问题时，GA-TS 的Cmax平均值为251，本文QGA 的Cmax平均值为248，减少了1.2%。 从整体性能来看，虽然GA-TS 求解问题用时较短，但QGA 首次达到最优结果所需的时间半数情况下均优于GA-TS，收敛速度平均提升了18.1%。

图9 为不同工件数量下QGA 与GA-TS 两种算法的目标值Cmax变化趋势图。

图9 不同工件数量下Cmax变化趋势图Fig.9 Trend plots of Cmax changes under different jobs

由图9 可以看到，在不同工件数量下，QGA 均获得了更好的初始解和最优调度解。 在获得相同最优解的情况下，QGA 的收敛速度更快。

4 结论

以最小化最大完工时间为目标，建立了带有运输的混合流水车间调度模型，基于Q-learning 设计了改进的遗传算法(QGA)求解调度问题。 采用Qlearning 对GA 的交叉概率和变异概率进行精确调整，显著提高了求解效率。 在不同规模下进行了仿真实验，并与GA-TS 对比分析，结果表明，QGA 在大多数情况下都能得到较好的解，且收敛性能也优于GA-TS，验证了其学习效果和优异性能。