基于Tracker的方位径向摆影响因素实验研究
胡雨迪 熊建文
(华南师范大学物理与电信工程学院 广东 广州 510006)
方位径向摆是一个多自由度非线性动力学系统[1].它的特点是:在方位径向摆的运动过程中,径向振荡(平行于杆)可以自发转变为方位振荡(垂直于杆),弹性杆、摆锤相互耦合,相互影响.所以说方位径向摆为三维空间中的弹性杆与摆锤的耦合振动[2].
理论分析指出,方位角、弹性杆直径、弹性杆长度、径向摆摆长等多因素对方位径向摆运动存在影响[2].但以往对方位径向摆的实验研究大多只讨论了方位角对方位径向摆运动的影响[3],本文利用Tracker软件追踪自制方位径向摆的运动,以更全面地探讨多因素对方位径向摆运动的影响.
1 实验原理与装置
1.1 理论模型
将一水平弹性杆一端固定在右侧刚性铁架台上,用一细绳拉紧弹性杆使弹性杆平行于地面.在弹性杆外端悬挂一摆球.左侧铁架台上固定有台虎钳,使用台虎钳控制摆球释放时的高度和方位角度.初始状态下,摆线应处于恰好紧绷的状态.
如图1所示,以水平垂直弹性杆方向为x轴,沿弹性杆方向为y轴,竖直垂直弹性杆方向为z轴建立直角坐标系.令摆线与z轴负方向的夹角为Φ.设弹性杆沿x方向的位移为x1,沿y方向的位移为y1,不考虑沿z方向的位移.弹性杆形变近似满足胡克定律,则弹性杆的势能函数为

图1 方位径向摆模型建立
(1)
摆线长为L1,弹性杆长为L2.设小球相对于弹性杆的末端在x、y和z方向的位移为x2、y2、z2.摆球的运动需满足几何条件
(2)
设弹性杆的线密度为ρ,则弹性杆的质量为m1=ρL2.弹性杆在x和y方向的速度分量为Vx(y),Vy(y),可知弹性杆的动能函数为
(3)
设小球的质量为m2,重力加速度为g,则小球的势能函数为[1]
V2=-m2gz2
(4)
小球的动能函数为
(5)
根据拉格朗日方程
L=T-V=T1+T2-V1-V2=
(6)
带入拉格朗日方程
(7)
求得该微分方程的解即方位径向摆的运动微分方程.
1.2 转化时间T的计算
如图2所示,令摆线在水平面上的投影与y轴负方向的夹角为θ,定义小球从开始运动到θ变为90°所经历的时间为方位径向摆的转化时间T.
1.3 实验装置
实验中,选取直径为22 mm的小球,使用电子天平称量得到小球质量为m=45.3 g.选取直径d分别为6 mm,8 mm,10 mm的弹性杆进行实验探究(图3).

图3 实验器材
实验仪器主要有铁架台、蝴蝶钳、不同直径的弹性杆、透明鱼线、小铁球、小铁架台、台虎钳、手机等.实验装置实物图,如图4所示.

图4 实验装置图
2 实验步骤
搭建实验装置,使用鱼线将弹性杆固定在大铁架台上,保证弹性杆平行于地面.将台虎钳固定在小铁架台上,通过调整台虎钳的位置和高度控制摆球释放的方位角.使用手机俯视拍摄1 min径向摆运动轨迹视频.分别改变释放时的方位角、弹性杆直径、弹性杆长度、径向摆摆长,录制不同情况下径向摆的运动轨迹.将视频导入Tracker软件进行分析处理(图5),获得径向摆运动轨迹,去除摆球释放前的视频片段,以2帧为间隔追踪摆球运动位置,分析释放后50 s内摆球的运动(约700个位点).将Tracker软件中小球的轨迹数据导出,使用绘图软件Origin绘制小球的运动轨迹,并计算径向摆的转化时间T.

图5 Tracker软件数据分析图
3 实验结果与讨论
3.1 径向摆轨迹与方位角的关系
在杆长L=25 cm,摆长S=45 cm的条件下,当θ=45°时,改变摆球释放时的方位角Φ(10°,45°,80°),得到径向摆轨迹并求出每种情况下的转化时间,结果如表1所示.为更清晰地观察径向摆轨迹,取2T内径向摆的运动轨迹,以Φ=45°和Φ=80°为例,结果如图6所示.此外,还进一步分析了2T内径向摆在x轴方向(图7)和y轴方向(图8)的衰减情况.

表1 不同方位角Φ下径向摆转化时间T(θ=45°)

图6 不同方位角Φ下2T内径向摆运动轨迹
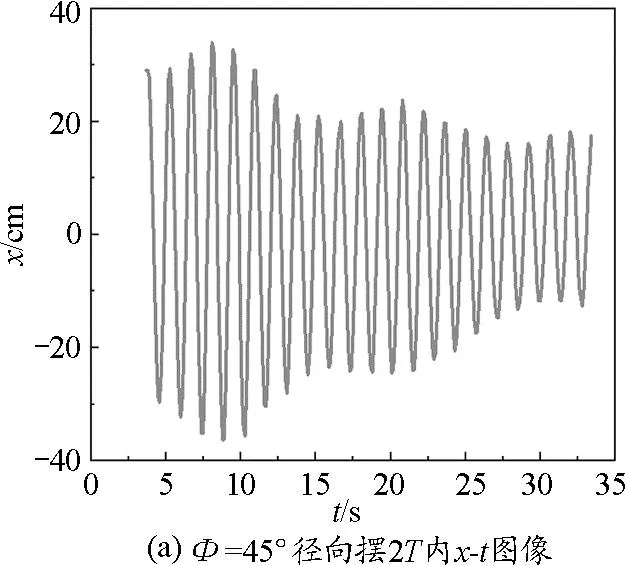
图7 不同方位角Φ下2T内径向摆x-t图像

图8 不同方位角Φ下2T内径向摆y-t图像
同样的,在杆长L=25 cm,摆长S=45 cm的条件下,当Φ=45°时,改变摆球释放时的方位角θ(10°,45°,80°),得到径向摆转化时间T如表2所示.图9中的(a)、(b)、(c)展示了不同方位角θ下2T内径向摆的运动轨迹.同理图10和图11分别展示了不同方位角θ下2T内径向摆在x轴方向和y轴方向的衰减情况.

表2 不同方位角θ下径向摆转化时间T(Φ=45°)

图9 不同方位角θ下2T内径向摆运动轨迹

图10 不同方位角θ下2T内径向摆x-t图像

图11 不同方位角θ下2T内径向摆y-t图像
实验中,θ的大小决定了摆球释放的位置,Φ的大小决定了摆球释放时的高度,也决定了初始状态摆球的重力势能.无论是方位角θ还是方位角Φ,当角度变大的时候,径向摆转化时间变短,径向摆在y轴方向的衰减会明显加快.
3.2 径向摆轨迹与弹性杆直径的关系
在弹性杆杆长L=25 cm,摆长S=45 cm,方位角θ=Φ=45°的条件下,使用直径d不同的弹性杆(6 mm,8 mm,10 mm),得到不同弹性杆直径下径向摆转化时间T,结果如表3所示.图12展示了当弹性杆直径d=8 mm和d=10 mm时2T内径向摆的运动轨迹.

表3 不同弹性杆直径d下径向摆转化时间T

图12 不同弹性杆直径d下2T内径向摆运动轨迹
实验结果表明,弹性杆直径越大,径向摆的转化时间越长.实验中,直径为6 mm的弹性杆无法让径向摆完成径向摆动的转化.由于弹性杆的直径与弹性杆的弹性系数有关,可以推测,若要让径向摆完成径向转化,弹性杆的弹性系数存在最大临界值.
3.3 径向摆轨迹与弹性杆杆长的关系
在弹性杆直径d=10 mm,摆长S=45 cm,方位角θ=Φ=45°的条件下,改变弹性杆的杆长L(15 cm,25 cm,35 cm),得到不同弹性杆杆长下径向摆转化时间T,结果如表4所示.图13展示了当弹性杆杆长L=25 cm和L=35 cm时2T内径向摆的运动轨迹.

表4 不同弹性杆杆长L下径向摆转化时间T

图13 不同弹性杆杆长L下2T内径向摆运动轨迹
实验结果表明,杆长越长,径向摆的转化时间越短.实验中,杆长为15 cm的弹性杆无法让径向摆完成径向摆动的转化.因此可以推测,若要让径向摆完成径向摆动的转化,弹性杆的杆长存在最小临界值.
3.4 径向摆轨迹与摆长的关系
在弹性杆直径d=10 mm,杆长L=25 cm,方位角θ=Φ=45°的条件下,改变径向摆摆长S(25 cm,35 cm,45 cm),得到不同径向摆摆长下径向摆转化时间T,结果如表5所示.图14展示了不同径向摆摆长下2T内径向摆的运动轨迹.实验结果表明,径向摆摆长越长,转化时间越长.

表5 不同弹性杆摆长S下径向摆转化时间T

图14 不同径向摆摆长S下2T内径向摆运动轨迹
4 结束语
本文通过Tracker软件追踪了方位径向摆的运动轨迹,研究了不同方位角的大小、弹性杆直径、弹性杆长度、径向摆摆长下方位径向摆的运动轨迹和转化时间.结果表明,当方位角θ或者方位角Φ角度变大的时候,径向摆转化时间变短;一定范围内,弹性杆直径越大,径向摆的转化时间越长;一定范围内,弹性杆杆长越长,径向摆的转化时间越短;径向摆摆长越长,径向摆转化时间越长.
综上所述,方位径向摆的运动受到多因素影响,该结论为未来进一步探究各因素与方位径向摆运动的定量关系提供参考.

