基于3D打印与轨迹追踪探究最速降线问题*

邱智宇 肖桂娜

(上海师范大学数理学院 上海 200234)

1 引言

伽利略于1630年提出疑问:给定两点A、B,且B与A的连线与水平面不垂直．若不计摩擦力,物体在重力作用下沿着怎样的曲线从点A滑到到点B,下滑的时间最短?[1]从直线到圆弧,再到最终旋轮线(最速降线)的确立[2-3],离不开伟大的物理学家建立在头脑中的实验室与计算系统．

随着现代信息技术的快速发展,依据最速降线的参数方程,本文利用SolidWorks软件建立3D模型,3D打印技术完成实体零件制作,拼装后探究物体在斜面上与最速降线上下落的运动情况,利用Tracker进行数据处理．应用现代信息技术研究物理运动观念,不仅能够高效、可视化地获得速度、位移随时间变化的关系,及时更新教学模式与理念,还可有效吸引学生兴趣,提高课堂教学效果．

2 实验原理

最速降线的确立一波三折,问题提出后吸引了很多著名数学家、物理学家的关注:牛顿、莱布尼茨、约翰伯努利和雅克比伯努利都研究过此问题,最终给出了正确的结果[2]．不同于伯努利应用费马原理类比获得结果,本文通过欧拉-拉格朗日方程推导最速降线的参数方程[4]．

如图1所示,A和B是平面上不在同一铅直线上的两点,在所有连接A和B的平面曲线中,存在一条曲线仅受重力作用,且质点从A点静止释放运动到B点沿这条曲线运动时所需时间最短．以A为坐标原点,建立平面直角坐标系,同时A也是半径为R的圆沿着x轴旋转的一个关注点,θ表示在转动过程中A点转过的角度．

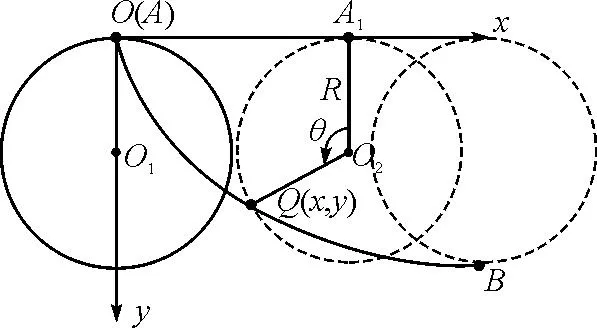
图1 最速降线原理图

不计摩擦阻力,质量为m的小球仅受到重力作用,所以机械能守恒

(1)

可以获得小球在曲线上运动的瞬时速度为

(2)

取Q上的极小一段距离ds,小球通过该段距离需要时间dt为

(3)

其中根据几何关系,可得

(4)

所以小球运动的总时间可以由积分得到

(5)

令

需要找到一个函数f(x)使得式(5)中的结果最小．通过欧拉-拉格朗日第二方程

(6)

由于F(y,y′)与x无关,所以

原方程可简化为

(7)

括号内的函数关系式为常数C,得

(8)

代入F(y,y′)后获得微分方程,利用分离变量法可以获得小球运动的参数方程

(9)

该结果被多人论证过充分性和必要性[5]．

此外,还可以获得小球沿最速降线下落的运动时间

(10)

上式中π、R、g都是常量,不随着释放高度的变化而变化,物体下落的时间与初始位置无关,最速降线也被称为等时降线．

3 实验方法

自制实验器材利用SolidWorks建立模型,应用轻薄光滑的树脂材料,光源为355 nm的高精度SLA光固化3D打印快速成型系统进行3D打印,建构的固件都具有高精度和尺寸的稳定性．

首先,如图2所示,在SolidWorks软件上建立3D模型,基于前视基准面建构草图,选择方程式驱动的曲线,并将最速降线的参数方程输入,选择合适的参数范围既可获得最速降线．使用直线将构建封闭,拉伸后获得构建的3D模型．

图2 利用SolidWorks建立3D模型图

3D打印选用的材料是树脂材料,在塑形前为乳白色粘稠液体,其黏度为497 cps,密度为1.14×103kg/m3,通过ASTM标准测试制件性能,具有光滑、不易弯曲变形等特性．

不同的曲线方程即可获得不同的3D构建,如图3所示,本次实验打印了最速降线与倾斜直线两种构件,拼装后完成最速降线的实验平台．小球选用能被磁性物质吸引的小铁球,利用磁铁实现同时释放小球的发射装置．

图3 最速降线3D打印实验装置实物图

将小球放置在发射台,抽离磁铁后,两个小球同时由静止沿斜面与曲面释放,在下滑过程中,可以清晰直观地从视频每一帧看到,相同时刻,沿着最速降线下落的小球先落到终点．

利用手机慢镜头录制实验视频,参数为1 080 p/240 fps,将实验视频导入Tracker软件中进行轨迹追踪,图4不仅可以直观看到小球在不同轨道上的运动情况,还可以获取位置、速度随着时间的变化关系．收集相关实验数据导入Origin软件进行图像绘制与数据分析．

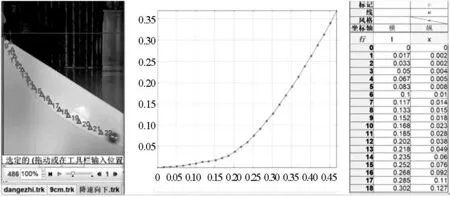
图4 利用Tracker追踪小球沿斜面下滑轨迹

最速降线的探究过程从“提出问题—设计实验—收集数据—分析结论—评估反思”符合物理学科核心素养中科学探究的要求,鼓励学生能积极应用现代技术设计创造实验用具,通过计算机软件处理解决问题,体现物理学科与时俱进的时代性[6],对学生今后的发展大有好处．

4 数据分析

本实验选用的小球质量为0.16 kg,自制实验仪器的设计基于直径为0.249 m的圆上的一点,沿着直线前进产生的螺旋线参数方程．断开磁力装置,两个小球由静止开始,同时从倾斜轨道与最速降线轨道下滑,得到如图5所示的水平位移与时间的关系．

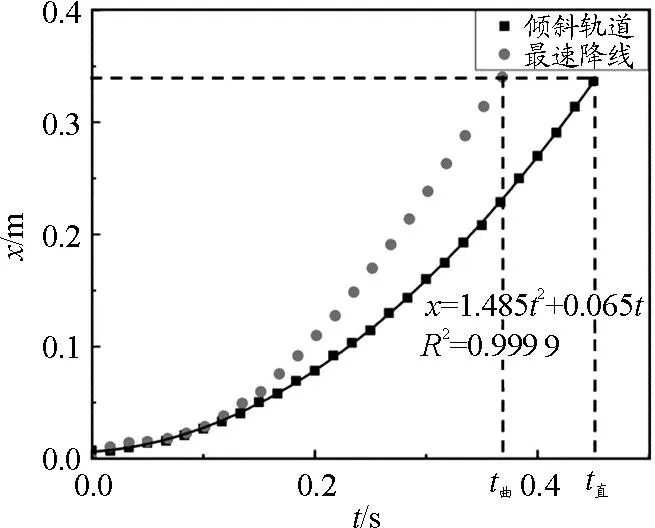
图5 两球分别从倾斜轨道与最速降线轨道下滑的水平位移与时间的关系

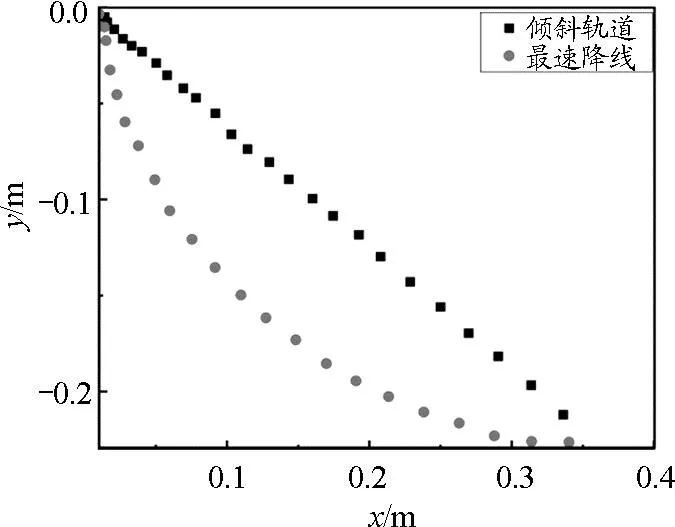
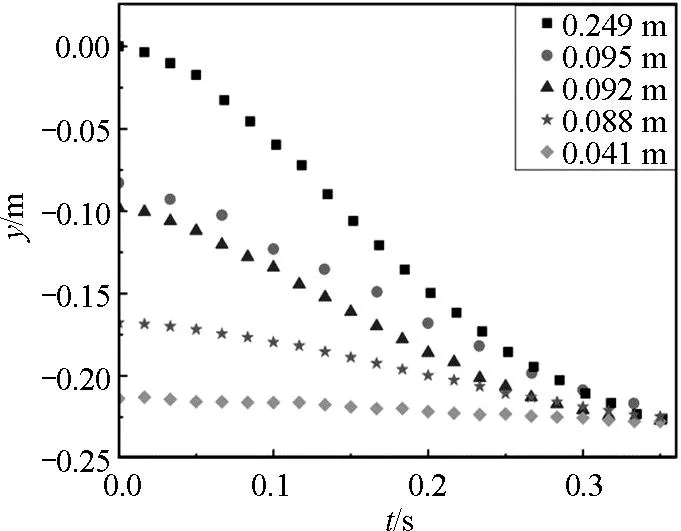
根据图5可知,当两球在水平方向到达终点时,t曲

表1 不同时刻,小球在两个轨道上的加速度比较

两球分别从倾斜轨道与最速降线轨道下滑的轨迹如图6所示.

图6 两球分别从倾斜轨道与最速降线轨道下滑的轨迹

表1对两段运动图像的斜率(运动的瞬时速度)进行计算,获得某一时刻的加速度．结合两者在图6中的运动轨迹可知:倾斜轨道上的小球做匀加速直线运动,运动过程中速度随着时间均匀增加,平均速度比最速降线小．而小球沿最速降线做加速曲线运动,加速度随着时间的增加而逐渐减小,在初始位置小球近乎垂直加速下落,让小球迅速加速获得快速通过后半程水平位移的能量,平均速度快,所以到达底部时间最短．

小球沿着最速降线的不同位置下落时的位移与时间数据如表2所示,图像如图7所示.

表2 小球沿着最速降线的不同位置下落时的位移与时间

图7 小球沿着最速降线的不同位置下落时的位移-时间图像

根据表2与图7可知:当小球分别从最速降线0.041 m、0.088 m、0.092 m、0.095 m和0.249 m处下落时,小球到达底端的时间均接近0.35 s．将上海地区的重力加速度g=9.764 m/s2与器材轨道的半径0.124 5 m代入公式(10)得小球下落时间的理论值,将实验值与理论值进行比对,相对误差均低于2%,考虑到Tracker软件读取信息时的频率,不能保证结束帧小球恰好落到轨道最低点,需要筛选数据多次测量取平均值．从实验上证明,沿着最速降线的不同位置下落的物体,下落时间具有等时性．

5 结论

最速降线的应用已渗透在建筑、运动场地等领域,它的确立从提出问题,推理解释,科学论证到现代可以通过3D打印技术与计算机软件进行实验验证,人类对物体在重力作用下的最快速下落研究逐步深入,不仅能够得到螺旋线的参数方程,更能高精度地还原最速下落的运动过程,并能发现物体从不同位置沿最速降线下落具有等时性．

希望教师在教学过程中,能够时刻联系物理学科的时代意义,将更多的研究方式呈现给学生,给学生夯实基础,开拓视野,为科学思维与探究的培养建构平台．