对高脚酒杯杯脚贴画在杯底球面成像通式的探究与拓展

郑通和

(宁夏育才中学 宁夏 银川 750021)

【原题】(第21届全国中学生物理竞赛预赛第6题)有一种高脚酒杯,如图1所示.杯内底面为一凸起的球面,球心在顶点O下方玻璃中的C点.球面的半径R=1.5 cm.O到杯口平面的距离为8.0 cm,在杯脚底中心处P点紧贴一张画片,P点距O点6.3 cm,这种酒杯未斟酒时,若在杯口处向杯底方向观看,将看不出画片上的景物.但如果斟酒,再在杯口处向杯底方向观看,将看到画片上的景物.已知玻璃的折射率n1=1.56,酒的折射率n2=1.34.试通过分析计算与论证解释这一现象.

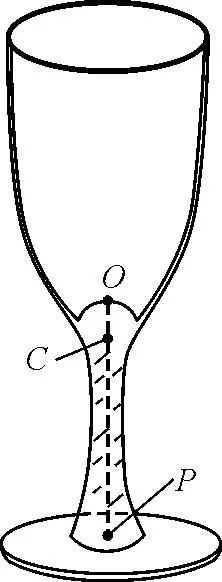
图1 高脚酒杯

1 高脚酒杯杯底是凸、凹球面成像的通式推导

1.1 杯底是凸球面的通式推导[1]

如图2所示,把高脚酒杯放平(杯脚靠左杯口靠右),分析成像问题.

图2 杯底是凸球面近轴光线成像光路

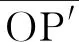
在△PAC中,由正弦定理有

(1)

考虑近轴光线成像:α、i都是小角度,可近似认为

sinα≈αsini≈i

则有

(2)

和角度几何关系

θ=i+α

(3)

得

(4)

在△CAP′中,由正弦定理有

(5)

同样考虑近轴光线成像:β、r都是小角度,可近似认为

sinβ≈βsinr≈r

和角度几何关系式

r=θ+β

(6)

得

(7)

在光路折射中,由折射定律

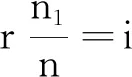
(8)

根据光路成像的距离几何关系,联立式(4)、(7)、(8)得

即得到一种高脚酒杯杯底是凸球面时杯脚底画片成像通式为

1.2 杯底是凹球面的通式推导

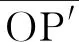
图3 杯底是凹球面近轴光线成像光路

在△PAC中,由正弦定理有

(9)

考虑近轴光线成像:α,i都是小角度,可近似的认为

sinα≈αsini≈i

得

(10)

由角度几何关系得

(11)

在△CAP′中,由正弦定理有

(12)

和角度几何关系

r=θ-β

(13)

同样考虑近轴光线成像:β、r都是小角度,可近似的认为

sinβ≈βsinr≈r

所以

(14)

由光路折射定律

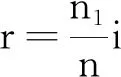
(15)

根据光路成像的距离几何关系,联立式(11)、(14)、(15)得

则得到高脚酒杯杯底是凹球面时杯脚底画片成像通式为

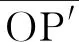
2 杯脚贴画在杯底是凸球面的成像位置

2.1 未斟酒时(图2)

n=n0=1,由通式得

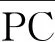
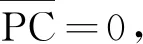
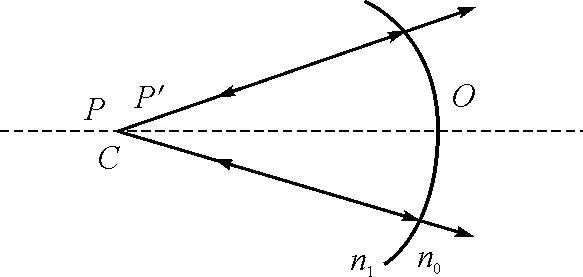
图4 杯底是凸球面近轴光线物象同点成像光路

n′=n0=1n=n1=1.56

证明和通式结论相一致.

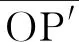
图5 杯底是凸球面近轴光线不成像光路

R=-1.5 cmn′=n0=1n=n1=1.56

解得

证明和通式结论相一致.

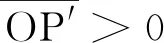
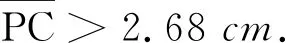
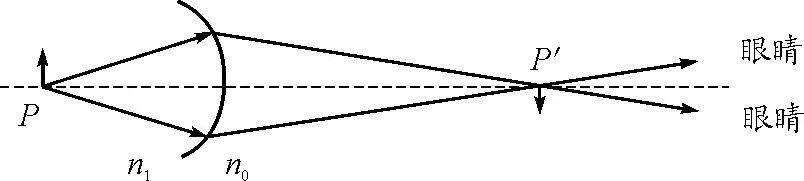
图6 实像P′通过眼睛在视网膜上二次成像光路

通过通式及作图证明了“这种酒杯未斟酒时,若在杯口处向杯底方向观看,能看到画片P上的景物”.并不是原题中所说的“将看不到画片上的景物”.

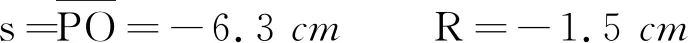
n′=n0=1n=n1=1.56

证明和通式结论相一致.

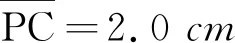
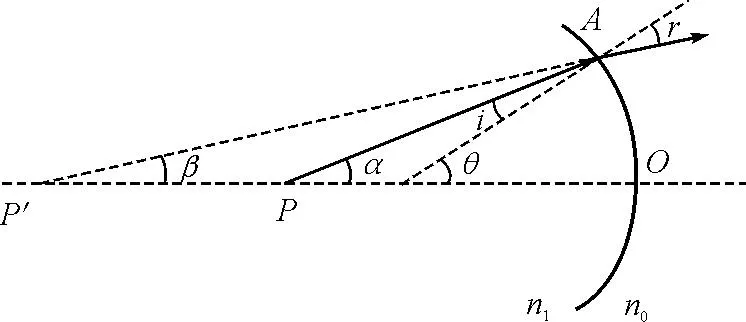
图7 杯底是凸球面近轴光线成像变深光路

n′=n0=1n=n1=1.56

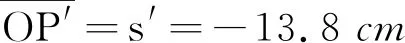
证明和通式结论相一致.

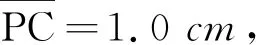
可确定虚像P′的位置,并可在杯口向杯底观看,见到像位变浅的P′(图8).

图8 杯底是凸球面近轴光线成像变浅光路

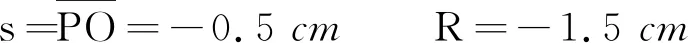
n′=n0=1n=n1=1.56

证明和通式结论相一致.

2.2 斟满酒后

当酒的折射率n=n2=1.34时,通式应为

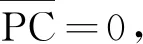
n′=n2=1.34n=n1=1.56

证明和通式结论相一致.

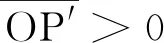
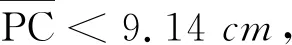
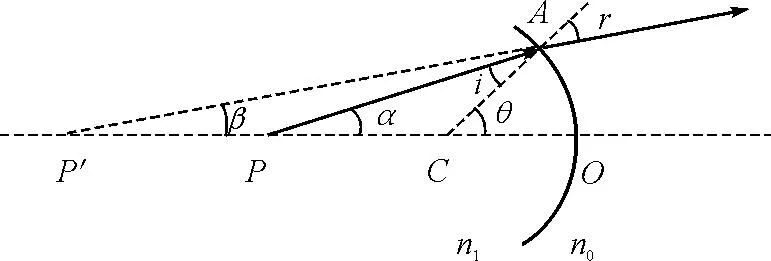
图9 杯底是凸球面近轴光线成像变深光路

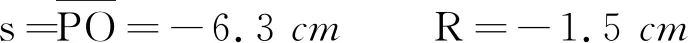
n′=n2=1.34n=n1=1.56

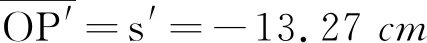
证明和通式结论相一致.

根据光在球面或不同介质面逐个成像法[3]可知,该像相对高脚酒杯中酒面可再次成像.

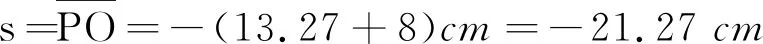
酒平面的曲率半径R∝∞,n′=n2=1.34,n=n1=1.56.

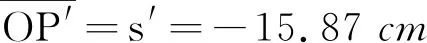
所成虚像在球面顶点O左侧15.87 cm处.

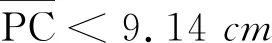
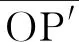
3 杯脚贴画在杯底是凹球面的成像位置

如图3所示,当n=n0=1,由通式

可知,当画片P距凹球面球心的距离

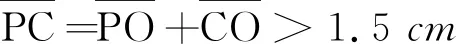
3.1 未斟酒时

如图10所示,n=n0=1,R=1.5 cm.

图10 杯底是凹球面近轴光线成像变浅光路

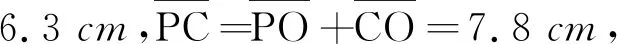
说明画片P成一虚像P′在凹球面顶点O的左侧1.61 cm处.

n′=n0=1n=n1=1.56

证明和通式结论相一致.

3.2 斟满酒后

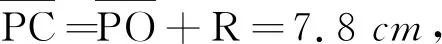
高斯公式验证

R=1.5 cmn′=n2=1.34n=n1=1.56

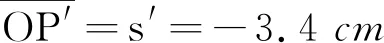
证明和通式结论相一致.

4 总结