推导平行板电容器电容表达式的两种方法
赵曰峰
(大连市第八中学 辽宁 大连 116021)

1 微元法
利用均匀带电平板的电场强度推导真空中平行板电容器电容表达式.
1.1 构建模型
构建带电半球壳模型计算无限大均匀带电平板产生的电场强度.
如图1所示,电荷面密度为σ的无限大带电平板产生的电场是匀强电场.
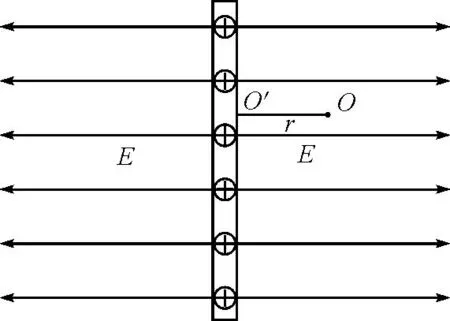
图1 均匀带正电平行板产生的电场
对于距平板距离为r的O点,其距离板最近的点为O′,对于O点电场强度可利用微元法求解.选择关于O′对称的两个微小平面面元dSi,如图2所示.

图2 两对称带电面元dSi在O点产生的电场强度
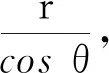
(1)

当球心角dαi→0时,球面面元dSi1等于平面面元dSicosθ,所以式(1)中dSicos3θ变为
dSicos3θ=dSicosθcos2θ=dSi1cos2θ
(2)

利用上式将式(2)化为
dSicos3θ=dSi1cos2θ=
(3)
将式(3)带入式(1)可得
(4)

因此由式(4)可知,O点的电场强度为
(5)
即无限大均匀带电平行板产生的电场强度为
EO=2kπσ
1.2 真空中平行板电容器电容表达式的推导
如图3所示,平行板电容器内部的电场可等效为两个相互平行的无限大平板内部产生的电场(这两个无限大平板带有相同电荷面密度为σ的等量异种电荷).

图3 平行板电容器内部产生的电场
由式(5)可得:
正极板产生的电场强度E+= 2πkσ.
负极板产生的电场强度E-= 2πkσ.
平行板电容器内部任一点的电场强度等效为两个相互平行的无限大平板在该点产生的电场强度的叠加,即
E=E++E-=2EO=4kπσ
因此电容器电压为
U=Ed=4kπσd
(6)
面积为S的平行板电容器的电荷量为
Q=σS
(7)
将式(6)、(7)带入电容的定义式,得出真空中平行板电容器的电容表达式为
2 极限法
极限法构造等效平行板电容器推导真空中平行板电容器电容表达式.
在真空中构造两个电荷面密度相同带异种电荷的同心球壳(球壳厚度不计),如图4所示,半径分别为RA、RB(半径满足关系RB-RA=d,d为定值),电荷量分别为+QA、-QB.在A球壳选取面元S,同一球心角下B球壳对应的面元为S′.

图4 两个电荷面密度相同带异种电荷的同心球壳

所以A、B球壳间电势差为
(8)
当RA→∞时,RA≫d,图4中球壳面元S和S′视为平行的平面面元,此时S≈S′.由于两球壳电荷面密度相同,则两面元电荷量相同,因此两球壳面元等效为平行板电容器.
两球壳间的电势差UAB即为构建的平行板电容器的电压,由式(8)可知电压为
(9)

所构建的平行板电容器的电荷量为
Q=σS
(10)
将式(9)、(10)带入电容的定义式,得出真空中平行板电容器的电容表达式为

3 充满介质时平行板电容器电容表达式的推导
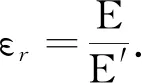
因此,充满介质的平行板电容器的电压为
(11)
面积为S的平行板电容器的电荷量为
Q=σS
(12)
由式(11)、(12)可得平行板电容器的电容表达式为
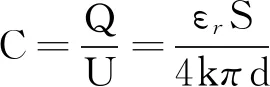
推导完毕.
4 结束语
本文通过利用高中生易于理解的两种方式推导了平行板电容器的电容表达式,使学生明确了电容表达式的由来,深刻体会了构建模型是解决物理问题的一种高效手段,感受到物理模型的魅力,同时解决了教师教学中的困难.推导过程利用微元法和极限法,合理外推,避免复杂的计算,通俗易懂,展示物理科学推理、科学论证的魅力,同时培养和拓宽了学生的科学思维能力,提升物理学科核心素养.

