一般情况下一维三原子链的求解及其色散关系*

成泓宣 胡建民 王月媛 牛 丽

(哈尔滨师范大学物理与电子工程学院 黑龙江 哈尔滨 150025)

晶格振动理论是固体物理学研究固体宏观物理性质和微观运动规律的重要理论基础,而一维原子链则是晶格振动理论的基本模型[1].关于一维单原子链和一维双原子链的研究已有大量文献报导[2-4].对于一维三原子链,文献[5]通过求解等间距和等恢复力系数这种特定原子链的色散关系进而分析其特点,在此基础上文献[6]则重点分析了原子质量对色散关系的影响规律,文献[7]则对这种特定情况下的一维多原子链色散关系进行了概括和总结.与特定的一维原子链相比,一般情况下的一维三原子链求解则更复杂,其物理性质也更丰富奇特、更具普遍意义,有必要深入探究.

本文拟求解一般情况下一维三原子链的色散关系,探究原子间恢复力系数对其色散关系的影响规律,相关研究结果既可以拓展固体物理教学内容,也可为科技工作者提供理论指导.

1 一般情况下一维三原子链模型及其色散关系

一般情况下的一维三原子链模型如图1所示.

图1 一般情况下的一维三原子链

近邻原子间距分别为a、b和c(晶格常数为d=a+b+c),设m1、m2和m3分别表示原胞内小原子、中原子和大原子质量,近邻原子间即小原子与中原子、中原子与大原子及大原子和小原子之间的恢复力系数分别为β1、β2和β3.适当选取坐标原点使第n个原胞内小、中、大原子平衡位置分别为nd、nd+a和nd+a+b,设离开平衡位置的位移分别为x3n、x3n+1和x3n+2.

简谐近似下建立晶格原子的运动学方程为

(1)

方程的试探解为简谐波

(2)

将上述试探解分别带入式(1)中得到关于振幅A、B和C的齐次线性方程组为

(3)

根据方程组有非零解的条件即系数矩阵的行列式等于零可得

αω6+γω4+λω2+δ=0

(4)

其中

α=-m1m2m3

γ=[(β2+β3)m1m2+(β1+β3)m2m3+

(β1+β2)m1m3]

λ=-(β1β2+β1β3+β2β3)(m1+m2+m3)

δ=2β1β2β3(1-cosqd)

由重根判别式

φ=γ2-3αλτ=γλ-9αδσ=λ2-3γδ

和总判别式

κ=τ2-4φσ

可确定方程解的个数,详解如下.

(1)当κ>0时,方程有两个虚根,没有物理意义故而舍去.

(2)当κ=0且φ≠0时方程有重根为

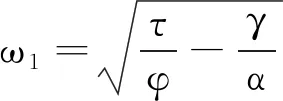
(3)当κ=0且φ=τ=0时方程有三重根

值得注意的是,在原胞内原子质量和恢复力系数都相等的情况下,当κ=0时q为确定值,则ω1、ω2和ω3为定值即此时的重根并不能给出一维原子链的色散关系;此外,当φ=0时意味着原子质量或恢复力系数等于零,则没有实际物理意义.所以,此时方程解个数的减少并不意味着一维三原子链色散关系向一维双原子链和单原子链过渡.

(4)当κ<0时,方程有3个不同实根即一维三原子链色散关系

(5)

由式(4)中的常数项和式(5)可知,色散关系与晶格常数d有关,而与原胞内原子间的相对距离无关.对式(5)进行数值拟合可得色散关系曲线如图2所示,低频声学支、中频光学支及高频光学支的频带分别为ω1、ω2和ω3,相应的频谱宽度分别为Δω1、Δω2和Δω3,频率禁带分别为Δω′和Δω″.当原子间距相等且m1=m2=m3=m、β1=β2=β3=β时频率禁带消失,从而一般情况下的一维三原子链色散关系可过渡为一维单原子链的色散关系[5].关于晶格常数对色散关系的影响已有文献报道,本文重点讨论恢复力系数对其色散关系的影响.

图2 一维三原子链简约布里渊区的色散关系曲线

2 恢复力系数对色散关系的影响

为分析不同原子间的恢复力系数对色散关系的影响规律,本文通过数值分析分别得到声学波和光学波频带顶和频带底分别随恢复力系数β1、β2和β3变化的关系曲线如图3所示.

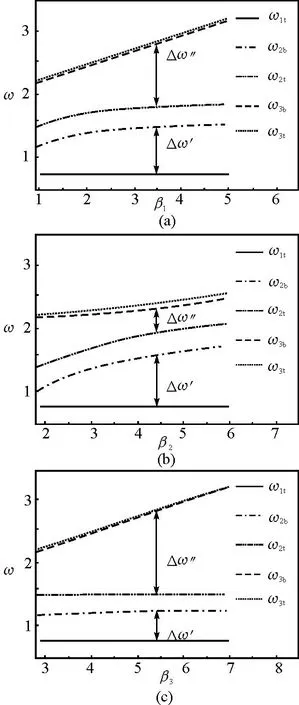
图3 一维三原子链频带顶和频带底随恢复力系数的变化

图3中ω1t为声学波频带顶,ω2t和ω2b分别是低频光学波的频带顶和频带底,ω3t和ω3b分别是高频光学波的频带顶和频带底.为简便起见,图3中的恢复力系数并不是其真实值,而是β1、β2和β33个恢复力系数的相对值,相应的格波频率也取相对值.由图3可见,不同的原子间的恢复力系数对格波频率、频谱宽度和频率禁带宽度的影响规律明显不同.

首先,不同的恢复力系数对各支格波频率的影响不同.不同原子间恢复力系数增大均会使光学波频率不同程度地升高.与光学波相比,声学波受恢复力系数的影响不大.

其次,不同的恢复力系数对频谱宽度的影响不同.相比而言,高频光学波频谱宽度Δω3几乎不受小原子和中原子间恢复力系数β1影响,而随β2的增大逐渐变宽,随β3的增大而变窄,这说明不同原子间的恢复力系数对高频支声子的能量分布范围影响不同;与高频光学波相比,中频光学波频谱宽度Δω2和低频声学波频谱宽度Δω1=ω1t基本不受恢复力系数影响.

最后,不同的恢复力系数对频率禁带的影响不同.两支光学波之间的频率禁带Δω″随小原子两侧恢复力系数β1和β3的增大显著变宽,而随β2的增大逐渐变窄并基本趋于恒定,前者是由于恢复力系数增大使高频光学支声子能量大幅度增高导致的,而后者则是由于中频光学支声子能量相比高频光学支声子能量更大幅度增高导致的;中频光学波与低频声学波之间的频率禁带Δω′随中原子两侧恢复力系数β1和β2的增大明显变宽,而随β3的增加则基本不变.由于恢复力系数对低频声学波的影响不大,所以频率禁带Δω′主要取决于中频光学波频带底的变化.总之,通过改变不同的原子间恢复力系数在理论上可实现对频率禁带宽度的精细调节.

与光学波相比,声学波频带顶ω1t受恢复力系数的影响较小,本文单独分析.

本文给出声学波频带顶ω1t随恢复力系数变化的关系曲线如图4所示.由图4可见,不同原子间的恢复力系数对声学波频率的影响明显不同,声学波频带顶ω1t随恢复力系数β1的增大而增大、随β2的增加而减小,而与β3无关,说明声学支声子的能量只受中原子两侧恢复力系数的影响,与大小原子间的恢复力系数无关.

图4 声学波频带顶随恢复力系数的变化

3 结论

本文通过求解一般情况下一维三原子链的色散关系,讨论恢复力系数对色散关系的影响.结果表明,在晶格常数和原子质量一定的情况下,色散关系与原子间恢复力系数密切相关.

高频光学支声子的能量随恢复力系数的增大显著升高,而中频光学支声子的能量仅随中原子两侧恢复力系数的增大而升高,而受大小原子间恢复力系数的影响很小.高频和中频光学波之间的频率禁带随小原子两侧恢复力系数的增大而加宽,随中大原子间恢复力系数的增大而变窄;中频光学波与低频声学波之间的频率禁带则随中原子两侧恢复力系数的增大而变宽,而受大小原子间恢复力系数的影响不大.与特定情况下一维三原子链相比,一般情况下的一维三原子链表现出更加丰富奇特的物理性质.本文相关研究结果是固体物理学基础理论的深入探讨,可为带通滤波器的工程设计提供理论指导.