基于系统辨识的航空发动机稳态燃油自抗扰控制

张家睿,汪 锐,刘舒恒,于 亮

(1.大连理工大学 力学与航空航天学院,辽宁 大连 116081; 2.大连理工大学 控制科学与工程学院,辽宁 大连 116081)

现代飞行器正朝着高空、高速、高机动性等方向不断发展,这对航空发动机的安全性和可靠性提出了越来越高的要求[1-2]。航空发动机安全稳定地工作离不开可靠的燃油控制系统。航空发动机燃油控制系统是由机械、液压、电子和电气等部件组成的复杂系统,其按照飞机的推力需求调节发动机的供油量。由于航空发动机的飞行环境复杂多变,同时存在零部件磨损、极端飞行天气、自身系统参数变化等情况,航空发动机燃油控制系统需要具有强鲁棒性[3],这也使得航空发动机稳态燃油控制器的设计变得非常复杂[4]。目前,自抗扰控制(Active Disturbance Rejection Control,ADRC)技术由于对模型的依赖程度低和动态补偿干扰等优点,正在被探索应用于设计航空发动机稳态燃油控制器。

ADRC的核心思想是将模型的不确定动态和外部扰动作为总扰动,构建扩张状态观测器(Extended State Observer,ESO)实时估计总扰动,进而将总扰动的估计值设计为前馈项实时补偿总扰动[5]。ADRC最初是非线性形式的,须调节参数多、输出抖动、稳定性不易保证等问题限制了ADRC在工程中的应用。Gao[6]在2003年提出了一种更简单、更易于实现的线性自抗扰控制器(Linear Active Disturbance Rejection Controller,LADRC),并将LADRC的调参问题简化为观测器带宽与控制器带宽的调节问题。近年来,越来越多的研究者开始将LADRC应用于航空发动机控制。Miklosovic等[7]将LADRC应用于航空发动机的解耦控制中,仿真结果表明LADRC具有良好的动态解耦特性。进一步地,张海波等[8-9]以静态解耦为基础,实现了发动机稳态与过渡态的多变量控制。为了进一步提高线性ESO (Linear ESO,LESO)的观测精度,谢振伟等[10]通过额外增加一个LESO来弥补原有LESO的观测误差,并将其应用到变循环发动机解耦控制中。

需要指出的是,LADRC的优异性能离不开合适的控制器参数。在LADRC中,参数b0是名义控制系数,决定了前馈补偿系数,进而影响对总扰动的补偿性能。针对参数b0的整定,Chen等[11]在假设调节时间已知的情况下,通过单调增大b0的方式来整定b0。然而,该方法只能确保在某一范围内试凑出合适的b0。对于航空发动机来说,多次试凑的成本较高,不合适的参数甚至会损坏发动机。另一个整定参数b0的思路是辨识系统的控制系数b,进而依据辨识结果整定b0。梁青等[12]设计了针对确定线性系统的控制系数辨识方法,基于该辨识结果可以快速整定参数b0。陈志翔等[13]在逐次精法[14]的基础上,设计了在线辨识控制系数的方法。需要指出的是,文献[12]、文献[13]只考虑被控对象动态已知或部分已知的系统。航空发动机的物理结构复杂,建模困难,在设计航空发动机稳态燃油控制算法时,被控对象的动态和控制系数b通常是未知的。b0整定为接近b时LADRC的总扰动补偿效果较为优异,因此,如何在被控对象动态未知的情况下准确辨识b是依据辨识方法整定参数b0的关键。

另外,LADRC将航空发动机中的未知高频动态归为总扰动,并使用ESO估计。为了保证对未知高频动态的准确估计,需要ESO具有较大的带宽,因此ESO的增益较高。然而,较高的ESO增益会放大测量噪声的影响,从而导致观测误差较大且观测器输出抖动[15]。如何改进ESO以实现使用低增益的ESO即可准确估计航空发动机未知动态,是设计航空发动机稳态燃油自抗扰控制器的一个难点。

本文拟基于系统辨识解决上述参数b0的整定问题与低增益ESO的设计问题。首先,基于CGS算法提出了一种一体化辨识控制系数与发动机未知动态的方法,基于控制系数的辨识结果,快速整定参数b0。其次,将未知动态的辨识结果引入ESO中构建IESO,由于未知动态的辨识结果中包含未知高频动态的信息,所以低观测器增益的IESO即可实现对总扰动的准确估计。最后,通过仿真验证了航空发动机转速对参考转速具有较好的跟踪性能。

1 问题描述

1.1 航空发动机稳态燃油控制

航空发动机的燃油控制逻辑如图1所示。本文考虑航空发动机在空中慢车、巡航等状态下工作,且稳态燃油控制律的输出未触发加速计划或线减速计划线。本文将设计稳态燃油控制律,保证在此工作状态下发动机转速能够很好地跟踪参考转速。

图1 航空发动机稳态燃油控制系统

本文考虑已知航空发动机转速动态的阶数为二阶,而其他动态未知,因此航空发动机转速的模型建立为

(1)

1.2 基于LADRC的航空发动机稳态燃油控制

在LADRC的框架下,模型中所有未知的部分被归结为总扰动,然后进行估计和补偿。因此,定义

x3(t)=f(x1,x2,w)+(b-b0)u(t)

(2)

(3)

基于式(3)设计以下形式的LESO：

(4)

(5)

λo(s)=(s+ωo)3

(6)

由于观测器带宽为ωo且是唯一需要被调节的观测器参数,因此选择合适的ωo即可保证ESO对转速及总扰动的准确估计。假设期望的转速轨迹为Nr,控制律设计为

(7)

(8)

通过配置合适的控制器增益k1、k2,即可保证发动机对参考转速的跟踪性能。

需要指出的是,为了保证LADRC的控制性能,工程上通常采用试凑的方法将参数b0整定为接近控制系数b。然而,航空发动机控制系统的控制系数是未知的,需要多次试凑才能够将b0整定为接近b,调参成本较高。调参过程中,不合适的参数b也可能诱使发动机进入超温超转等状态,损坏发动机。因此,将LADRC应用于航空发动机稳态燃油控制的第一个难点是参数b0的整定。另外,航空发动机中包含高频的热力机械动态。在LADRC的框架中,这些动态包含在总扰动x3中。为了实现对总扰动的准确估计,高频动态的频率需要在观测器带宽内,这就需要较高的观测器增益。然而,较高的观测器增益会放大测量噪声的影响,造成观测器输出抖动。因此,将LADRC应用于航空发动机稳态燃油控制的第二个难点是如何改进ESO以实现使用低观测器增益即可准确估计航空发动机未知动态。本文考虑上述两个难点,设计了一种基于系统辨识的航空发动机稳态燃油自抗扰控制器。

2 控制器设计

控制器设计的思路是：对式(1)中的未知动态f和控制系数b进行一体化辨识,f的辨识结果中包含高频未知动态,将f的辨识结果加入ESO中,从而降低观测器增益,并基于b的辨识结果整定b0。将f的辨识结果与总扰动的估计值一起作为前馈项,即可补偿未知动态f的影响。IESO与控制律组成了所设计的航空发动机稳态燃油自抗扰控制器。以下首先介绍系统辨识方法,再介绍IESO及航空发动机稳态燃油自抗扰控制器的设计。

2.1 航空发动机转速模型辨识

本节研究未知动态f与未知控制系数b的一体化辨识。首先,考虑用一个离散模型近似式(1)的动态。航空发动机是典型的非线性系统,而非线性向回归滑动平均(Nonlinear Auto Regressive Moving Average with Exogenous Inputs,NARMAX)模型是非线性系统的一种输入输出描述,能够很好地表征非线性系统的动态特性,因此本文考虑选取NARMAX模型作为航空发动机转速系统的离散化表征[16-19]。采用向前差分的方法得到式(1)的NARMAX模型如下：

y(k)=2y(k-1)-y(k-2)+T2f(k-2)+T2bu(k-2) (9)

f与b的辨识问题转化为式(9)中的f(k-2)和b,本文采用CGS算法[20]辨识这两项。

考虑使用以下线参数模型：

(10)

式中：y(t)为模型的输出;θi为待估计的模型系数;Φi为多项式结构项,Φi=[φi(1),φi(2),…,φi(N)]T,其中i=1,2,…,27,φ1=u(k-1),…,φ3=u(k-3),φ4=y(k-1),…,φ6=y(k-3),φ7=u(k-1)2,…,φ10=u(k-1)u(k-3),…,φ13=u(k-3)2,φ14=y(k-1)2,…,φ27=y(k-3)2;e(t)为模型的误差;N为数据长度。由式(10)可推得：

Y=ΦΘ+E

(11)

式中：Y=[y(1),y(2),…,y(N)]T;Φ=[Φ1,Φ2,…,Φ27];Θ=[θ1,θ2,…,θ27]T;E=[e(1),e(2),…,e(N)]T。

辨识的思路为整定合适的模型系数矩阵Θ,使得式(10)逼近数据点时刻的式(9)。具体地,考虑结构项冗余及Φi之间的相关性导致的数值病态问题,采用正交化算法进行求解,辨识思想为：采用正交分解的方法处理式(11)中的结构项矩阵Φ,然后依据ERR准则[20]选取模型结构项,将要求的预测精度或者迭代阈值作为停止条件,最后回代求解待估参数。算法的具体步骤如下。

① 对矩阵Φ进行Q、R分解,记RΘ=G,令Q=[q1,q2,…,q27],G=[g1,g2,…,g27]T,将式(11)转换为Y=QG+E。

② 初始化结构项qi=Φi,i=1,2,…,27。

④ 以先前选择的结构项为基底,对其余结构项qi进行施密特正交化。

⑤ 重复步骤③～步骤④,反复迭代求解完成Φ的排序、Q的更新与R的构建。

⑥ 依据RΘ=G回代求解Θ。

(12)

(13)

2.2 IESO及航空发动机稳态燃油自抗扰控制器

(14)

(15)

式(13)～式(15)构成了所提出的改进的航空发动机稳态燃油自抗扰控制器 (Improved Aircraft Engine Steady State Fuel Active Disturbance Rejection Controller,IADRC)。将式(15)代入式(1)可得：

(16)

3 IESO收敛性及闭环系统稳定性分析

3.1 IESO的收敛性分析

(17)

(18)

本文考虑观测误差系统即式(18)满足以下假设。

假设2：测量噪声v(t)是有界的,满足|v(t)|≤g。

假设3：存在ρ>0使得

依据以上假设得到以下IESO观测误差收敛性的结论。

定理1：考虑满足假设1～假设3的观测误差系统即式(18),对于任意的μ>g,存在ωo>0和t1>0,使得

|ei(t)|≤μ,i=1,2,3,t>t1

证明：求解(18)可得

(19)

(20)

|(A-1B1)i|≤ζ

(21)

(22)

由于A为Hurwitz矩阵,因此存在一个有限时间t1>0,使得：

(23)

(24)

(25)

|qi(t)|≤|(A-1B2)i|+|(A-1eωoAtB2)i|,i=1,2,3

(26)

对于上式的A和B2有A-1B2=[v(t) 0 0]T,根据假设2中噪声的有界性,由式(23)可得：

(27)

(28)

由式(21)～式(28)可得：

(29)

因此有

(30)

由式(19)可知：

|ηi(t)|≤|[eωoAtη(0)]i|+|pi(t)|+|qi(t)|,
t≥t1,i=1,2,3

(31)

(32)

因此,在考虑观测噪声的条件下,对于任意μ>g,存在ωo>0和有限时间t1使得|ei(t)|≤μ,定理1得证。

由式(22)和式(25)可以看出,ζ和σ与假设2中的常数ρ有关,并且ρ越小,ζ和σ也越小。同时式(32)表明,对于确定的观测器带宽ωo,当ζ和σ越小时,由于参数li选择的特殊性,式(32)中不等式右侧的值也会越小。因此当ρ越小时,对于要求的观测误差精度μ,就可以配置更小的观测器带宽ωo来满足要求。

3.2 闭环系统的稳定性分析

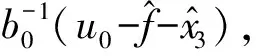
(33)

(34)

(35)

式中：

定理2：考虑满足假设1～假设4的式(35)存在控制器参数k1、k2和时刻t1,使得eN(t),t≥t1对于任意有界输入r(τ),τ∈[0,t)是有界的。

证明：式(35)的解为

eN(t)=eA1teN(0)+φ(t)

(36)

φ(t)的有界性。由定理1可得存在常数ωo>0使得：

|ei(t)|≤μi,i=1,2,3,t≥t2

(37)

式中：γ=k1μ1+k2μ2+μ3+ρ+c。令B4=[0γ]T,可得：

(38)

(39)

由于A1是Hurwitz矩阵,存在一个有限时间t3>0,使得：

(40)

令t1=max{t2,t3},有

(41)

由式(41)可得：

(42)

由式(38)、式(41)、式(42)可得：

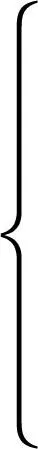
(43)

eA1teN(0)的有界性。由式(40)可得：

(44)

由于

(45)

由式(44)和式(45)可得,对于任意t≥t1,下列不等式成立

(46)

定理2得证。

4 仿真验证

本文基于MATLAB/Simulink进行数值仿真,仿真系统中的双转子涡扇发动机模型采用真实的实验数据构建,可以很好地模拟发动机的运行。发动机模型中转子动态为二阶,其他具体信息未知,因此发动机动态可以用式(1)描述。发动机模型的输出是相对换算转速,高压转子的相对换算转速N2由下式计算得到：

(47)

式中：Ncur为当前转速;Nmax-des为最大设计转速。

控制目标是控制高压转子的相对换算转速N2从71.4上升并稳定在78。首先采用本文所提出的方法对未知动态f与未知控制系数b进行一体化辨识。将步长设置为0.001 s,输出的初值设置为y(1)=y(2)=y(3)=0.1,辨识所用的控制输入为u(t)=100[sin(40t)+sin(60t)]+300+10rand,其中rand函数的功能是产生在0～1之间分布的随机数。得到b的辨识结果为5.2,f的辨识结果为[y(k)-2y(k-1)+y(k-2)](0.001)-2-5.2u(k-2),依据b的辨识结果将参数b0整定为5.2。

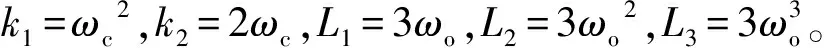
b0不同时的转速曲线如图2所示。可以看出采用b的辨识结果整定的b0=5.2的系统调节时间较短,并且没有明显的超调。b0为b的辨识结果,可以避免复杂的参数试凑过程。

图2 b0不同时的转速曲线

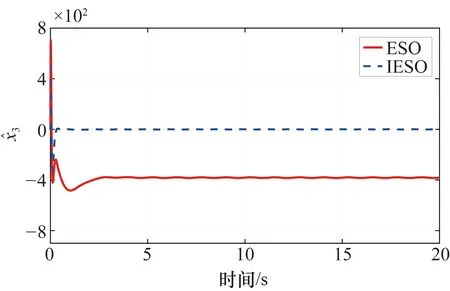
图3 ESO和IESO的总扰动估计曲线

图4 ESO和IESO的估计误差曲线

燃油流量曲线与加减速计划线如图5所示,可以看出,燃油流量一直在加减速计划线内,因此发动机的燃油流量一直由稳态控制器调节。

图5 燃油流量曲线与加减速计划线

假设控制指标需要将相对换算转速稳定在[77.99,78.01]范围内,调节观测器增益,最终将ESO的观测器增益整定为ωo=65,将IESO的增益整定为ωo=20,此时的相对换算转速曲线如图6所示,转速在IADRC和LADRC控制下达到均衡并稳定在期望转速,并且IADRC的超调与振荡小于LADRC,说明在同样的控制指标下,IADRC的观测器增益较小,IESO可以有效降低观测器增益。

5 结束语

自抗扰控制器应用于航空发动机稳态燃油控制存在参数b0整定困难、观测器增益过高的问题。针对这两个问题,本文设计了基于系统辨识的航空发动机稳态燃油自抗扰控制器,利用未知控制系数b的辨识信息快速整定b0并证明了所设计的IESO的收敛性,进一步证明了控制系统的有界输入和有界输出的稳定性,从而说明了所设计的控制器能够保证航空发动机转速对参考转速的跟踪性能。最后通过数值仿真验证了所设计的航空发动机稳态燃油自抗扰控制器的有效性。