基于时差法的复杂转子系统声发射源定位算法

王丕彤, 于 洋

(沈阳工业大学 信息科学与工程学院, 辽宁 沈阳 110870)

复杂转子系统在电力、机械制造和石油化工等领域有着广泛的应用,碰摩是复杂转子系统中最常发生的故障之一,而碰摩位置的精准定位对设备的安全运行十分重要。在现有的声发射(Acoustic Emission,AE)源定位方法中,基于到达时差(Time Difference of Arrival,TDOA)的方法成为较常用的AE源定位方法。在这种方法中,最直接影响定位精度的是时延估计算法。

刘增华等[1]针对实际工程中,材料中不同方向的AE信号的传播速度不一致的问题,提出了一种先使用预构建数据库的方法记录各个传感器的TDOA,再筛选得到真实AE源与训练映射AE源差值最小的点,即AE源。李晓崧等[2]针对复杂材料表面AE源定位问题,提出了一种基于信号相似度的方法,使用自适应小波算法对复杂材料原始AE信号进行降噪并重构后再定位。鞠双等[3]对采集的复杂材料表面AE信号先进行小波分解,再分析被处理信号,最后采用时差定位算法,计算得到AE信号沿纵轴与横轴方向的传播规律。袁梅等[4]针对航天器中复杂材料AE源定位技术精度低等问题,将AE信号进行自适应分解重构后使用广义互相关时差定位算法。

基于上述研究,本文引入一种基于平滑相关变换(Smoothed Coherence Transform,SCOT)的双加权二次互相关时延估计算法,计算复杂转子系统的碰摩声发射源信号的到达时间差,再利用Hilbere差值法对相关峰值进行锐化,减小在碰摩过程中噪声的干扰,以获得较为精确的时延估计结果,提高复杂转子系统的碰摩声发射源定位的精度。

1 算法研究

1.1 互相关时延估计算法

设两个传感器探头采集的AE信号模型为

x1(n)=s1(n-τ1)+n1(n)

(1)

x2(n)=s2(n-τ2)+n2(n)

(2)

式中：s1(n-τ1)和s2(n-τ2)为AE信号;τ1和τ2为AE源到探头的时间;n1(n)和n2(n)为高斯白噪声。

x1(n)和x2(n)的相关函数R12(τ)可以表示为

R12(τ)=E[x1(n)x2(n-τ)]

(3)

将式(1)和式(2)代入式(3)可得

R12(τ)=E{s(n-τ1)s(n-τ1-τ)+

E[s(n-τ1)n2(n-τ)]}+

E[s(n-τ2-τ)n1(n)]+

E[n1(n)n2(n-τ)]

(4)

由于s(n)、n1(n)与n2(n)不相关,可得：

R12(τ)=E[s(n-τ1)s(n-τ1-τ)]

=Rs[τ-(τ1-τ2)]

(5)

互相关函数的性质表明,当τ-(τ1-τ2)=0时,R12得到的极大值τ是两个探头间的时延[5]。

在上述推导中,默认情况下,AE信号与噪声之间以及噪声与噪声之间没有相关性[6]。

但是,在工程实践中该结果并不理想,由于只能使用有限时间平均而不能使用无限时间平均,使得噪声对这种短时近似引起的相关函数的影响不能被忽略。

上述问题将导致R12(τ)相关峰值和TDOA值的精度降低,因此,广义互相关[7]技术应运而生。

常用的广义加权函数如表1所示[8]。

表1 常用的广义加权函数

表1中,Gx1x2(f)在互相关中表示信号x1(n)和x2(n)的互功率谱。

在二次互相关中,将第一次自相关看作x1(n),第一次互相关看作x2(n)。

根据Wiener-Khinchin定理,可得：

(6)

式中：G12(ω)为信号x1(n)和x2(n)的互功率谱。广义互相关方法[9-11]是将信号互功率谱在频域加权运算,然后进行逆变换,得到两组信号间的广义互相关函数：

(7)

1.2 基于SCOT双加权二次互相关时延估计算法

广义双加权二次互相关法是利用二次相关算法对广义互相关算法进行优化的时延估计算法,结合了两者的优点,其算法框图如图1所示。

图1 基于SCOT双加权二次互相关算法框图

x1(n)、x2(n)为两路传感器采集信号,经过FFT方法处理,获得信号自相关函数和互相关函数,再对互相关函数进行第一次加权处理后,与自相关函数结合,得到二次互相关函数,再对其进行第二次加权处理后得到互功率谱函数,通过傅里叶逆变换(IIFFT)得到互相关函数,通过峰值检测找到其峰值的对应坐标,即两个信号之间的时延。

1.3 Hilbere差值法

Hilbert变换相当于在广义互相关时延估计算法中将峰值提取转变为对应的过零点提取。通过这种处理方法,可以消除一部分外界干扰。在正常情况下,该算法会获得准确的TDOA值。

但该算法仍然有不足之处,具体如下。

① 当处理来自复杂、恶劣环境中的信号时,信号中存在大量噪声干扰将导致代表TDOA估计值的零点周围发生波动,进而使信号波反复过零点。

② 当对一个信号进行持续监测时,采集到的数据量将是巨大的,这会使算法得到许多的过零点。

这两种情况都会使过零点位置无法判断,进而造成TDOA值准确度大幅降低。为解决这两种情况提出了Hilbert差值法[12],表达式如下：

(8)

Hilbert差值法框图如图2所示。

图2 Hilbert差值法框图

Hilbert差值法对峰值检测进行优化,使互相关函数中峰值点两边的相关性降低,主峰值点得到锐化,过零点位置明显,提高时延估计的精度。

1.4 AE源定位算法

AE源的一维线定位模型是由2个传感器探头构成,如图3所示。

图3 一维线定位模型

碰摩源信号到达探头1和探头2的时间分别为t1和t2,时间差为Δt。探头间距离为L,碰摩源与探头1距离为D,设AE源信号波传播速度为v,则表达式如下：

(9)

AE源的二维线定位模型是由4个传感器探头构成[13],如图4所示。

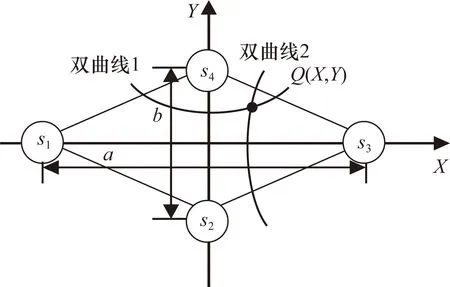
图4 二维平面定位模型

碰摩源信号探头s1和探头s3间的时间差tx构成双曲线1,碰摩源信号探头s2和探头s4间的时差ty构成双曲线2,探头s1和探头s3距离为a,探头s2和探头s4距离为b,碰摩源Q(X,Y)位于双曲线1和2的相交点上,碰摩源Q的坐标为

(10)

(11)

Lx=Δtx·v

(12)

Ly=Δty·v

(13)

2 仿真实验

选用两个信号进行仿真实验,设余弦信号s1(n)、s2(n)为仿真实验信号,表达式如下：

s1(n)=0.5e-10Ntsin(2π·f0·t)

(14)

s2(n)=0.5e-10Ntsin(2π·f0·t1)

(15)

式中：fs=1 MHz,f0=100 kHz,N=1 000,其信号仿真图如图5所示。

图5 信号仿真

在两个信号中分别加入信噪比为-10 dB和-15 dB的高斯白噪声后,用广义互相关、基于SCOT的双加权二次互相关和Hilbert差值法改进后的双加权二次互相关时延估计算法求两个信号的互相关函数,如图6所示。

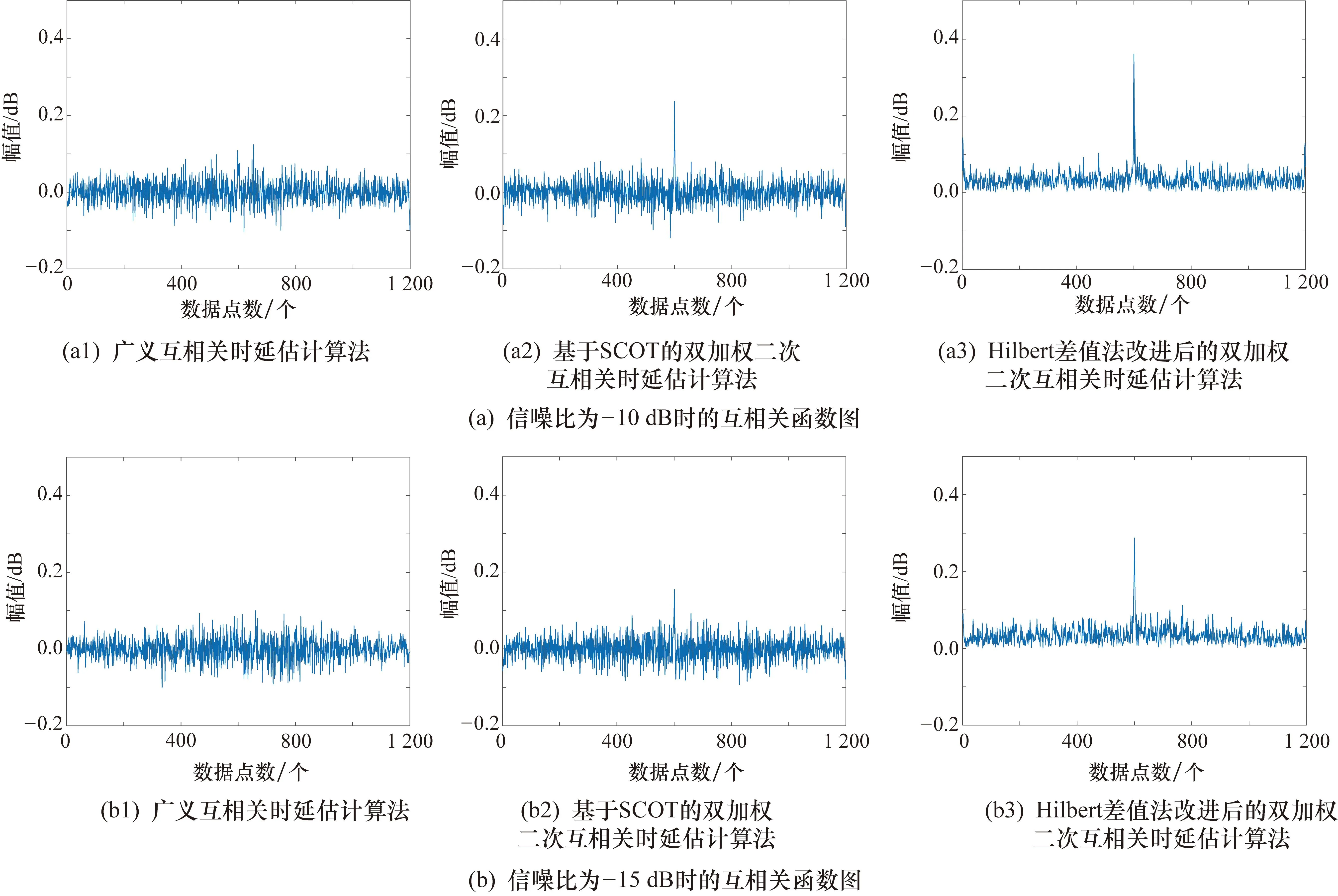
图6 时延估计算法仿真对比图

由图6可得,当信噪比为-10 dB和-15 dB时,广义互相关时延估计算法的互相关函数图出现伪谱峰,无法得到正确的时延,双加权二次互相关时延估计算法和Hilbert差值改进后的双加权二次互相关时延估计算法仍然可以得到正确的时延。但是后者的互相关函数图明显更优,所求时延更加准确。

根据仿真实验的结果可见,基于SCOT双加权二次互相关时延估计算法适用的信噪比范围广泛,在低信噪比条件下可以保持稳定的时延估计能力,Hilbert差值法的引入,锐化了互相关函数中的相关峰值,使获得的时延值更精确。

3 转子系统碰摩AE源定位实验

3.1 实验数据与分析

被测部件转子系统外壳可近似为圆柱体,在外壳上布置12路传感器对其进行实时监测,转子系统外壳模型及传感器布置阵列如图7所示。

图7 转子系统外壳模型及传感器布置阵列

第一层6路传感器探头接收AE源信号如图8所示。第二层6路传感器探头接收AE源信号如图9所示。

图8 第一层6路传感器接收AE源信号图

图9 第二层6路传感器接收AE源信号图

分别利用广义互相关算法、基于SCOT双加权二次互相关算法和Hilbert差值法改进后的双加权二次互相关算法对传感器探头采集的信号进行时延估计,分别从3种算法算出的时延值中随机选取了100对数据分成10组比较其平均相对误差,结果如图10所示。

图10 平均相对误差折线图

由图10可得,基于SCOT的双加权二次互相关算法所求时延的平均相对误差小于广义互相关算法。用Hilbert差值法改进后的双加权二次相关算法所求时延值的平均相对误差小于改进前算法。

对被测部件一维上定位点进行10次实验,实验结果如表2所示。

表2 被测部件一维上定位点(直线定位)实验结果

对被测部件二维上定位点进行10次实验,实验结果如表3所示。

表3 被测部件二维上定位点(平面定位)实验结果

表2和表3中时差值由Hilbert差值法改进后的双加权二次互相关时延估计算法求出,再根据1.4节中的定位算法计算AE源位置,得到的结果与实际AE源位置之间的误差满足AE定位要求,具有实际意义。

3.2 定位实验结果

计算复杂转子系统碰摩AE源信号中传感器探头之间的时延值进行AE源定位,定位图如图11和图12所示。

图11 被测部件上碰摩AE源一维定位

图11和图12中,黑色六芒星表示传感器,红色星号表示定位点。图11为被测部件上碰摩AE源在一维上的定位图,图12为被测部件上碰摩AE源在二维上的定位图。

4 结论

实验结果表明,在复杂转子系统的碰摩AE源定位实验中,基于SCOT的双加权二次互相关时延估计算法相比于广义互相关时延估计算法,具有波动小、峰值尖锐和抗干扰能力强的特点,可以求得准确的时延值。Hilbere差值法的引入,锐化了相关峰值,使获得的时延值更精确,从而可获得更高的定位精度。