基于RBF神经网络的进气压力控制方法研究

乔彦平, 郭迎清, 高红岗

(1.西北工业大学 动力与能源学院,陕西 西安 710072; 2.中国航发四川燃气涡轮研究院 高空模拟技术重点实验室,四川 绵阳 621700; 3.西北工业大学 民航学院,陕西 西安 710072)

高空台是能够模拟航空发动机地面和空中飞行条件的大型试验设备,对航空发动机的研制和发展起着至关重要的作用[1]。高空台试验过程中,在进行被试发动机的推力瞬变、遭遇起动、加减速等过渡态试验时,发动机空气流量变化速率达到5～30 kg/s2,对高空台进气压力控制提出了极大的挑战[2-3]。而进气压力模拟精度作为高空模拟试验中非常重要的一项指标,直接关系到试验的有效性[4-5]。

进气压力控制系统是一个复杂系统,受到多种非线性因素的影响,被控对象难以精确建模。传统的PID控制原理简单,但对进气压力的控制往往需要有经验的操作员手动参与来保证过渡态时压力调节的偏差在规定允许范围内。这种方式必然存在速度过快和重复性过高等方面的问题,且当前主流算法都是在PID基础上进行小的修改[6-7],无法应对状态量发生改变给系统控制精度和动态性能带来的问题。

为提升过渡态过程中的压力控制精度,需开展压力自适应控制方法研究,实现过渡态时压力的自适应控制。以深度学习为代表的人工智能技术为进气压力控制问题开启了一条新的研究路径,即基于数据驱动的机器学习方法在过渡态压力控制中的应用。根据不同工作状态下的输入输出数据流,运用神经网络等方法构建一个近似模型[8-9],用来预测压力控制系统的调节信号[10-11]。

本文针对进气压力过渡态控制,首先设计了基于RBF(Radial Basis Function,径向基函数)神经网络的最优控制方法,然后在对试验数据进行分析的基础上,对面向进气压力控制问题所设计的RBF神经网络进行了训练,最后对基于该RBF神经网络的压力控制系统的调节品质进行了测试。

1 基于RBF网络的最优控制架构设计

1.1 输入输出信号的选取

利用RBF神经网络进行建模,首先需要确定神经网络的输入和输出。通过分析影响高空台进气压力控制系统的因素,选取的输入输出信号如图1所示。

图1 RBF神经网络的输入输出选取

图1中,Si表示系统压力在i时刻的设定值和反馈值以及发动机在i时刻的状态参数,Ai表示所有调节气体压力的阀门在i时刻的控制量。

1.2 控制策略方案和架构设计

针对气体压力控制中非线性、高耦合的性质,基于数据驱动构建系统控制模型,采用机器学习的方法探索过渡态最优协同控制策略。为实现过渡态最优协同控制策略,神经网络的训练和根据实时数据获取最优控制策略是需要研究的重点问题。基于机器学习获取最优控制策略的方案如图2所示。

图2 基于机器学习获取最优控制策略的方案

RBF神经网络的训练是一个重要的环节,RBF神经网络隐藏节点数量和基函数的参数确定对网络结果影响较大。采用梯度下降法作为训练方法,均方误差作为损失函数,训练RBF神经网络,形成输入输出信号的非线性映射关系模型,根据实时输入信号快速输出预测的状态。基于数据驱动的智能控制原理架构如图3所示。

图3 基于数据驱动的智能控制原理架构

2 基于RBF神经网络的进气压力控制系统模型设计

2.1 系统结构分析

系统的气路原理如图4所示,其中阀门212连接高压常温气源与混合器,阀门213连接高压负温气源与混合器,通过2条管路将不同温度的气流混合,调节这2个阀门就可以调节混合器内空气的温度;阀门231、阀门232连接混合器与大气,用于调节混合器内压力;阀门241、阀门242连接混合器与前室,用于调节进气压力。

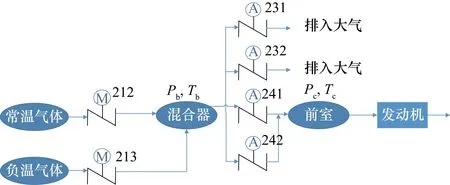
图4 系统的气路原理

系统运行过程中,设定混合器和前室压力值,要求混合器和前室气压始终维持在这一给定值附近,但由于发动机状态的改变,会影响到前室和混合器内压力的变化,为维持混合器和前室气压的稳定,需要阀门231、阀门232、阀门241、阀门242这4个阀门参与调节,这些阀门协同运作,可保证混合器和前室气压的稳定。

2.2 问题分析

将压力控制问题的建模作为一个函数拟合问题,搭建神经网络模型,经过大量数据训练拟合出输入与输出间的关系,最终使模型能够预测不同输入情况下系统的输出,从而达到自动控制的效果。依据之前的分析,混合器与前室之间通过阀门连接,混合器与前室各自压力变化对彼此都会产生影响,是高度耦合的,而阀门231、阀门232和阀门241、阀门242也协同作用于整个系统,进而维持各个腔内空气压力的动态平衡,也是高度耦合的,因而不适合将各个容器或阀门单独拆分出来进行分析。因此,神经网络的模型输入应包含发动机转速、空气流量、混合器压力设定值、混合器压力测量值、前室压力设定值、前室压力测量值这6个变量,模型输出为阀门231、阀门232、阀门241、阀门242的开度控制量。通过对试验数据的分析,在调节系统压力平衡过程中,阀门232和阀门242的开度几乎不变,在此为了降低网络维度,确定模型输出为阀门231、阀门241的开度控制量。

2.3 模型结构及设计

RBF神经网络的基本思想是用RBF作为隐单元的“基”构成隐含层空间,这样就可以将输入矢量直接映射到隐含层空间,而不需要通过权连接。当RBF的中心点确定以后,这种映射关系也就随之确定了。

RBF神经网络应用于进气压力控制时,每个时刻的输入为系统当前状态和发动机状态,输出为对各阀门的控制量。RBF神经网络隐含层神经元的激活函数为RBF,并将输入空间转换为到最近中心点的距离空间,把输入向量从低维映射到高维,将线性不可分问题转换为线性可分问题。

构建的RBF神经网络结构如图5所示。作为3层单向传播的前馈网络,其包含了输入层、隐含层和输出层。

图5 RBF神经网络结构图

输入层由信号源节点组成,表示输入维度,隐含层是非线性的,其采用高斯函数作为RBF,从而将输入向量空间转换到隐含层空间,使线性不可分的问题变得线性可分。隐含层的神经元个数一般取2的指数,由试验可知,隐含层由32个径向基神经元组成时效果最好。输出层则是由线性加权映射得到的。在RBF网络架构中,x=[x1,x2,x3,x4,x5,x6]T为网络模型的输入向量,y=[y1,y2]T为输出向量。

RBF选用高斯基函数,则从输入层到隐含层的公式为

(1)

式中：bj为方差;‖·‖为欧几里得范数;Cj=[cj1,cj2,…,cj6]T为第j个基函数的中心节点,cj为可以决定该基函数围绕中心点的宽度的参数且是可以自由选择的,在这里,cj的初始值随机生成,随着网络的训练而不断更新;m为隐含层节点个数。

从隐含层到输出层的公式即为隐含层的加权表达式：

(2)

式中：wkj为第j个RBFhj到输出yk的加权。

网络输出的损失函数J为

(3)

训练模型采用沿负梯度下降的方法使损失函数最小。

3 仿真分析

对图4中手动调节过的进气压力控制系统进行测量,采集了4组试验实测数据,数据的特征包括发动机转速、空气流量、混合器压力设定值、混合器压力测量值、前室压力设定值、前室压力测量值、阀门231和阀门241开度控制量,其中,前6个特征作为网络的输入X,后2个特征作为网络的参考输出Y。将这4组(Datasheet1、Datasheet2、Datasheet3、Datasheet4)试验实测数据作为训练数据和测试数据,对所建立的RBF神经网络进行训练和测试,验证设计的基于数据驱动的压力控制方法的可行性。首先选取小规模数据对RBF神经网络进行训练和测试,然后利用大规模数据进行验证。

3.1 模型的训练和测试

3.1.1 小规模数据仿真

选取Datasheet1的全部数据和Datasheet2的前25 000组数据,共56 595组数据作为训练数据;选取Datasheet2剩余数据(共62 907组数据)作为测试数据。部分训练数据的形式如表1所示。

表1 部分训练数据

将RBF网络训练了100轮,训练时长为3 195.83 s。测试时,遍历所有测试数据的时长为34.51 s,平均每条数据测试时长0.000 5 s(即反映从获取到一组输入进而给出预测输出的时间,在给定试验环境中预测响应时间小于1 ms)。阀门231开度控制量和阀门241开度控制量的真实值与预测值对比如图6所示。

图6 小规模数据预测效果

3.1.2 大规模数据仿真

随机选取Datasheet3、Datasheet4中的一半试验数据作为训练数据;选取Datasheet3、Datasheet4的所有数据作为测试数据。RBF网络训练用时15 332.18 s,训练完成后,对网络进行测试,测试用时201 s,共372 223组数据,平均每条数据测试时长0.000 5 s。阀门231开度控制量和阀门241开度控制量的真实值与预测值对比如图7所示。

图7 大规模数据预测效果

由图7可见,在试验末尾阶段,阀门开度的数据变化幅度大,控制器无法及时调整开度,所测量的数据为失真数据。针对Datasheet3、Datasheet4试验数据中的这些极端数据,将这2组数据中的异常数据删除,形成数据集Datasheet3_1、Datasheet4_2。在Datasheet3_1、Datasheet4_2数据集中随机取一半数据作为训练数据,用全部的数据进行测试。网络训练时长为12 486.76 s,训练完成后,对网络进行测试,测试用时160.64 s,平均每条数据测试时长0.000 5 s。阀门231开度控制量和阀门241开度控制量的真实值与预测值对比如图8所示。

3.2 结果分析

由上述试验结果计算RBF网络的预测值与真实值的误差,误差计算公式为

(4)

小规模数据因数据量少理论上应预测得更准确,而大规模数据相对而言预测误差较大。表2对误差情况进行了统计,其结果也反映了RBF网络在小规模数据上的误差小于大规模数据。

表2 RBF神经网络控制模型测试结果误差统计

由表2可以看出,通过小规模数据训练后的RBF神经网络的预测结果与真实值的误差较小,大规模数据测试结果的误差比小规模数据测试结果的误差大了一些,但误差均处于较小的水平。小规模数据只对采集的小部分数据进行了训练和测试,RBF网络训练小规模数据更容易收敛,因此在小规模数据上误差较小。试验中,小规模数据测试结果的误差与大规模数据的误差的差别不大,当精度要求不高时,采用小规模数据对网络进行训练就可以满足要求且训练时间更短。由表2可知,阀门最大控制误差为阀门231的最大控制误差,数值为3.11%。阀门231的平均控制误差在采用大规模数据时最大,为1.04%,阀门241的平均控制误差在采用大规模数据和删去异常数据后的大规模数据时是一样的,都为0.47%。由于大规模数据的阀门231平均控制误差和阀门241平均控制误差较大,取大规模数据的2个阀门平均控制误差来衡量RBF网络控制的表现,整个RBF神经网络控制系统的平均误差为阀门231和阀门241平均控制误差的总和的平均数,为0.755%,因此均值误差约为1%。

通过该方法,不需要人为地对控制系统进行精准参数调节,也不需要对各个控制阀门进行关系解耦,RBF神经网络使系统能够达到自动控制的效果。结果表明,RBF神经网络预测的自动控制策略误差较小,并且预测时间较短,控制效果良好。

4 结论

通过本文研究,得到结论如下：

① 以高空台的进气压力调节系统为对象,设计了基于RBF神经网络的最优控制架构,搭建了RBF神经网络模型,为研究工作提供了基础。

② 利用4组试验实测数据作为训练数据和测试数据,对所建立的RBF神经网络进行训练和测试。测试结果表明所设计的控制方法针对被试发动机加减速等过渡态试验进气压力控制问题,进气调节阀预测控制精度峰值误差小于4%,平均误差约为1%,预测响应时间小于1 ms,精度和预测实时性能够满足过渡态压力的控制要求。

③ 总体而言,本文所设计的基于RBF神经网络模型的最优控制架构是可行的,不仅减少了有经验的操作员手动参与的步骤,而且预测时间较短,可以满足进气压力控制实时性的要求。