温度敏感涂料校准误差实验研究

欧阳波, 高丽敏, 葛 宁, 王 磊

(1.西北工业大学 动力与能源学院,陕西 西安 710072; 2.翼型、叶栅空气动力学国家级重点实验室,陕西 西安 710072)

温度敏感涂料(Temperature Sensitive Paint,TSP)技术具有高空间分辨率、全域测量等优势,在航空航天领域具有广阔的应用前景[1]。但由于测量方式的间接性,其测量结果中往往包含来源广泛的误差,使得其测量精度受到多方面的耦合影响。为了适应高精度测量技术发展的需要,明确TSP技术的误差大小对其测量结果的定量化和可靠性验证具有重要意义。

TSP技术的误差主要有三类：第一类误差来自于TSP自身化学和物理性质的影响,Romano等[2]在应用TSP研究医学上凝血过程时指出,涂料经历玻璃化温度后其荧光产率将发生变化,而这种特性变化在短时间会持续存在。Mclachlan等[3]应用TSP进行边界层转捩探测时发现,涂料在实验过程中出现了光降解现象,而照明强度、涂层厚度和涂层中的分子浓度也会对测量结果造成影响[4-5]。第二类误差来自于涂料测量系统精度的影响,如光电探测器的噪声、非线性等[6]。第三类误差来自于吹风实验阶段,如模型的气动变形[7]、气体自发光等[8]。为了对上述误差进行耦合计算,基于误差传播方程的全因子分析方法可用于测量结果的不确定度计算。Cattafesta等[9]全面分析了TSP测量过程中的误差来源,并基于误差传播方程对TSP的测量误差进行了耦合计算,得到了被测模型上像素级的测温不确定度分布。Kasai等[10]采用类似的思路重点评估了寿命法中运动模糊、温度效应对PSP(Pressure Sensitine Paint,压力敏感涂料)/TSP测量结果的影响。但是在上述误差分析过程中,校准误差极少被单独进行考虑,并且由于第三类误差的影响,基于全因子误差分析得到的结果难以具备通用性。TSP校准实验是建立TSP信号强度和温度映射关系的独立实验,其结果直接影响TSP温度测量精度。此外,其具有相对确定的测量系统和实验流程,因此针对校准实验进行全因子误差分析具备必要性和可行性。

为了进一步提升和验证TSP技术的可靠性,本文基于自主搭建的TSP校准系统,分析和评估了校准实验中的主要误差来源及其不确定度;结合TSP特性曲线拟合算法提出了TSP校准误差的耦合计算方法,并采用统计方法验证了其准确性。研究结果可用于指导建立标准化、精细化的TSP校准流程,并可作为TSP校准误差定量化计算方法。

1 TSP校准方法

1.1 TSP校准原理

如图1所示,TSP由温敏发光分子和高分子聚合物黏结剂组成。处于基态的温敏发光分子在受到某个波长的入射光激发后会跃迁到激发态。激发态属于不稳定状态,温敏发光分子在返回基态的过程中会产生某种特定波长的辐射光,而此过程受温度的影响。因此便形成了TSP发光强度与温度之间的关联。将两者之间的关系进行定量化的过程即为TSP校准,其结果可用高次多项式来表示[11]：

(1)

图1 TSP校准原理示意图

式中：I和Iref分别为涂料在不同温度T和Tref下的发光强度,下标“ref”为参考工况,用于将发光强度进行归一化;Ai为多项式系数,下标“i”为对应的多项式次数。在获得如式(1)所示的TSP温度-发光强度特性关系式后,即可通过探测模型表面TSP的发光强度变化获取温度分布。

1.2 TSP校准系统

为了拟合如式(1)所示的TSP温度-发光强度特性关系式,需要获取在不同温度下的TSP发光强度数据。这样一个温度可控、发光强度可探测的系统即为TSP校准系统。

本文在团队已开发的PSP静态压力校准系统[12]的基础上对其进行了优化改造,建立了TSP校准系统。如图2所示,激发装置采用了405±17 nm国产高稳定性连续发光LED准直阵列光源;光电探测设备采用了高灵敏度背板制冷的14位科学级CCD相机搭配Nikon 17-35 mm变焦镜头,并采用了与TSP光谱适配的615±15 nm带通滤光片,实现了对TSP辐射光波段信号的高效捕捉和对噪声的有效阻断。校准舱为目标TSP的载体,其本体为一可密闭舱体,顶部留有亚克力透明视窗,为光源和相机提供了一条较为广阔的光路。校准舱耦合了控温系统、控压系统,以提供校准所需的实验工况。

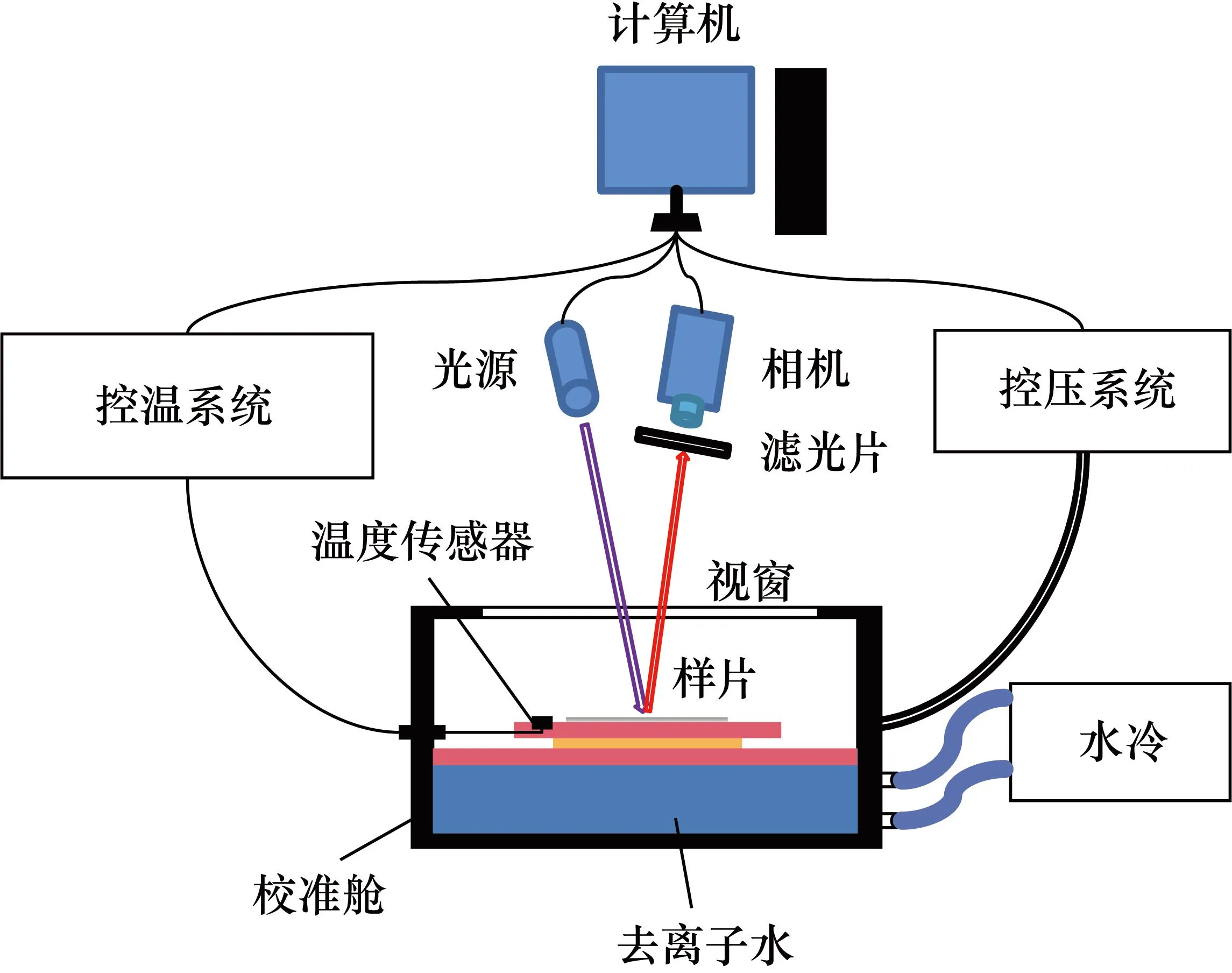
图2 TSP校准系统示意图

1.3 TSP校准数据处理流程

基于CCD相机的TSP校准系统可获取不同温度工况下的TSP发光强度图像。须采用图像处理方法减小误差对校准结果的影响。如图3所示,首先是读入图像,其中包含了光源开启时采集的TSP发光图像和光源关闭时采集的暗背景图像。在随后的减去暗背景图像这一步骤中,将两者作差即可消除部分系统误差的影响。接着,对图像进行图像帧平均,以此减小时域随机误差。然后,选取发光强度较为均匀的区域对图像进行区域平均处理,降低空间随机误差对结果的影响。重复上述过程,读取并处理所有温度工况下的图像,选定参考工况I(Tref)后可通过比处理获得每个温度下的光强比,最后可通过拟合获得TSP温度-发光强度特性关系式。

图3 图像处理方法流程图

2 误差来源及其影响分析

在进行误差传递分析之前,需要明确各种误差源所产生的误差类型,以便采取不同的耦合计算方法对其进行误差合成。根据TSP的测温原理,TSP校准实验中的测量误差主要有3个来源：涂料性质、校准系统和拟合误差。

2.1 涂料性质

涂料性质误差源主要包括涂料不稳定性、涂层厚度不均匀性和发光分子浓度不均匀性。其中,发光分子浓度不均匀性和涂层厚度不均匀性的大小主要取决于喷涂工艺和喷涂人员的技术水平。事实上,即使由同一个人员按照同样的工序和手法进行两次喷涂也难以保证喷涂效果的一致性。两个误差源均具有强烈的空间随机性。

涂料不稳定性是指由于TSP长时间放置导致的温敏发光分子特性降解,TSP在高温环境下工作导致的结构变化、不可逆的特性失活,TSP由于强激励条件或长时间激励等因素引起的特性衰变。具体表现为TSP绝对发光强度的衰减和温度敏感性的改变。本文所用TSP均在现场配置、喷涂并校准,校准时长不超过30 min,因此其停留在相对高温工况的时间较少,故不考虑涂料不稳定性的影响。

2.2 校准系统

2.2.1 CCD相机

与CCD相机有关的误差源主要包括6项,分别为暗电流噪声(Dark Noise)、光子散粒噪声 (Shot Noise)、读出噪声(Readout Noise)、偏置噪声(Bias Noise)、场景噪声(Scence Noise)和非线性噪声(Nonlinear Noise)。其中,暗电流噪声为温度和CCD相机工作时间的函数,可通过减去暗背景图像(在同样的相机参数和环境下关闭光源时所采集的图像)进行消除。光子散粒噪声与光子到达相机感光芯片的时间有关,属于随机变量,在时域上服从泊松分布。读出噪声包含了CCD相机系统组件在将电荷转化为数字信号的过程中产生的噪声的总和,属于随机噪声。偏置噪声来源于CCD相机自带的预置电压,通常为固定值。场景噪声也被称为CCD相机不均匀性,指的是像素之间由于制作工艺或材料的微弱区别导致的增益差别。非线性噪声是指在不同的入射光强度水平下,CCD相机输出的数字信号渐渐不再与探测得到的光信号成正比,从而造成输出的光强偏差。

2.2.2 光源

理想的光源应该具有高激发强度、高稳定性和发光均匀的特点。其中,高激发强度有利于高信噪比TSP图像的获取,即有利于降低其他误差源对测量结果的干扰,但其本身并不是误差源。与光源相关的误差源主要包括光源激发强度的不稳定性(以下简称“光源不稳定性”)和光源激发强度的不均匀性(以下简称“光源不均匀性”)。光源不稳定性由光源激发强度在短时间内的随机波动和长时间工作产生的漂移引起,因此可细分为光源随机波动和光源漂移这两个不同类型的噪声。光源不均匀性受到模型几何特征变化和光照角度变化的影响,使得到达模型表面的光源激发强度不均匀,进而引起TSP“光致发光”的不均匀。

2.2.3 校准舱

校准舱耦合了控温系统和控压系统,由此产生控温误差和控压误差。对TSP而言,压力本身是一个误差源;但控压误差属于高阶小量,在本文中予以忽略。控温误差主要源于样品盘上的温度不均匀性和热电阻的测量精度,其直接影响测量到的温度值和 TSP发光强度,是不可忽略的误差因素之一。

2.3 拟合误差

本文中的拟合误差并不是指拟合残差,而是指拟合过程中原始拟合数据所携带的误差对最终拟合结果误差分布的影响。TSP技术具有间接测量的特性,对温度的测量依赖于由多组离散校准工况点数据拟合得到的温度-发光强度特性曲线。因此,校准实验中用于构建温度-发光强度特性曲线的原始拟合数据(光强比、温度)皆有一定的误差范围,最终得到的特性曲线必然由于各组数据点之间的相互约束导致其误差范围受制于拟合算法。

3 误差传递分析及校准误差计算方法

3.1 误差源分类及其计算定义式

根据第2节中对TSP校准过程中的误差来源及其影响的分析,结合各误差源的来源和特点,其分类详情如表1所示。发光分子浓度不均匀性、涂层厚度不均匀性、光源不均匀性和场景噪声这4个误差源由于其结果均表现为引起模型表面不同空间位置的绝对发光强度不一致,尽管其在单个像素上具有确定性,但是在无法实现像素级别的上述4种误差的定量甄别的现实条件下,将其综合影响视为空间不均匀性噪声。控温误差由校准舱内热电阻的测量精度决定,为±0.2 K。表1中部分符号含义如下：t为校准时单帧图像曝光时间;I为测得的图像某像素上的光强;T为温度;k(带不同下标)为需要通过实验评估得到的部分误差源的相对误差系数;符号“≈”表示其计算过程忽略了高阶小量误差的影响。

表1 误差源分类详情

表1中不同类型的误差分别采取不同的计算方式。系统误差之间的耦合直接通过代数法计算,对于随机误差之间的耦合影响,则通过标准差耦合公式进行计算：

(2)

式中：Urandom为耦合随机误差;i、j分别为不同的误差源序号;σi为误差源i的随机误差;ρ为不同误差源之间的相关系数。基于上述误差源之间的独立性,计算中取ρij=0。

对于随机误差和系统误差之间的耦合影响,采用均方根法(Root-Sum-Square,RSS)[13]对其数值进行计算：

(3)

式中：U为耦合误差;Ubias和Urandom分别为系统误差和随机误差。

3.2 误差传递分析及耦合计算方法

根据1.3节中的TSP校准数据处理流程,减去暗背景图像和图像帧平均最先进行,再减去暗背景图像后,可消除环境噪声和偏置噪声的影响。

至此,所得图像上每个像素的发光强度组成中还包含以下误差量：非线性噪声In、光源漂移Idr、光源随机波动Iw、空间不均匀性噪声Iun、光子散粒噪声Ish和读出噪声Ir。在进行区域平均和比处理后,可得：

(4)

式中：下标“ideal”表示想要获取的理想值;T、Tref分别为设定温度和参考温度;δIT、δIref为对应温度工况下测得的光强中所包含的误差耦合值,可结合式(2)、式(3)计算;δ(IT/Iref)为比处理后每个光强比所包含的测量误差。本文采用误差传递公式[12]对其进行计算,即

(5)

结合式(4)和式(5)可得一系列不同温度工况下包含误差的光强比处理结果,根据同步采集的温度数据(同样包含测量误差ΔT),需要对曲线进行拟合从而得到与式(1)对应的TSP温度-发光强度特性曲线。以基于最小二乘方法的三次多项式拟合为例,根据拟合原理,拟合系数Ai和校准数据之间满足以下关系：

(6)

δ(IT/Iref)fit=

(7)

式中：i、j分别为多项式次数(i=0,1,2,3)和原始数据组数量;δ(IT/Iref)fit为最终得到的拟合曲线所包含的误差。可通过自编程序实现上述计算过程。

4 误差源不确定度评估方案

4.1 读出噪声

读出噪声大小与相机帧率相关。本文中CCD相机工作模式不变,因此可将此参数假定为固定值。参考读出噪声常用测量方法[14],拟定测量方案如下：将相机的曝光时间调至最小值(与采用的CCD相机型号有关,如本文采用的PCO.2000最小曝光时间为500 ns),设置相机内部工作温度为253 K(同样取决于CCD相机性能),关闭相机镜头盖。此时由于相机无任何外界光进入,因此所拍摄图像中只包含了读出噪声这一项随机误差。连续采集多帧图像(本文采集了1 000帧用于计算),通过贝赛尔公式计算某像素点上的标准差作为读出噪声：

(8)

式中：Ipixel,i为第i帧图像上选定像素的光强。

4.2 光源不稳定性

光源的不稳定性包含了光源激发强度短时间内的随机波动和长时间工作产生的漂移。根据此特点,采用CCD相机正对光源的方式进行拍摄,单帧曝光时间为定值(根据CCD相机采集到的光强大小确定,不可过曝,本文中为2 μs),连续拍摄90帧图像。一共拍摄两组,第一组拍摄完毕后关闭相机,而光源仍保持运行,30 min后再拍摄第二组,并拍摄相应的暗背景图像。

估计光源随机波动不确定度时只在时域上进行,针对单个像素,不考虑以下误差：① 由于每组连续拍摄的90帧图像用时极短,因此不考虑同组图像之间的光源漂移;② 两组图像的发光水平并未显著改变,因此不考虑两组图像间由光源漂移造成的二次的CCD的非线性误差。

综上分析,图像标准差中只包含了光子散粒噪声和读出噪声两种随机误差的影响。考虑光源漂移时,将第一组图像和30 min后拍摄的第二组图像在减去暗背景图像和图像帧平均后,根据式(2)和式(3),可得光源不稳定性误差的相对误差系数计算方式：

(9)

式中：I0和I30分别为经过图像处理后在0时刻和30 min后同一像素上的帧平均光强;σ0和σ30为对应的标准差。

4.3 非线性误差

CCD非线性是指在不同的入射光强度水平下,CCD相机输出的数字信号渐渐不再与输入的光信号成正比。在上述实验基础上保持光源发光模式不变,调节相机曝光时间使图像光强覆盖相机的整个满阱范围,以此模拟入射光由弱到强的过程[15]。在每个曝光时间下连续拍摄80帧图像,取其算术平均值作为该曝光时间下的强度,并通过最小二乘线性拟合得到CCD相机的理想线性范围。CCD的非线性度kn可表示为

(10)

式中：IN(t)为曝光时间t下N帧图像的算术平均值(1≤N≤80),I80(t)即表示通过80帧图像的算术平均值得到的拟合值。

4.4 空间不均匀性

空间不均匀性包含了场景噪声、涂料不均匀性和光照不均匀性的耦合影响,其绝对大小受到空间位置变化的影响。由于引入了涂料的影响,因此通过计算校准时获得的不同工况下减去暗背景图像后的原始图像上有效区域的标准差σ(IT),结合其余噪声的影响,可将其不均匀度kun表示为

(11)

5 结果及分析

5.1 校准范例

以某型国产TSP的校准结果为例：选择在278～353 K范围内对涂料进行校准,温度调节步长为5 K,光源为外触发模式,通过外部信源进行触发,以避免校准过程中长时间激发可能造成的涂料性能衰减。在278 K时,基于相机满阱值(16 384)和涂料发光强度确定单帧曝光时间为3.5 ms,此时涂料发光强度平均水平大致为10 700。此外,为了在校准工况下避免涂料玻璃化温度的影响(本文所用TSP的玻璃化温度约为298 K),测试开始前在303 K下对涂料进行了预加热。

图4为不考虑误差时278～353 K温度范围内的TSP温度-发光强度特性关系校准曲线,基于最小二乘的三次多项式拟合方法,其具体拟合系数如表2所示。

表2 拟合系数

图4 TSP温度-发光强度特性关系校准曲线

5.2 误差源不确定度评估结果及分析

读出噪声为最先引入原始图像的噪声量,因此其不确定度需要被首先确定。根据式(8),读出噪声为Ir=±2.3。

图5为光源不稳定性测量结果,图中横坐标为图像数量(N),纵坐标为用灰度阶表示的光强。其中,E为80帧(排除了前10帧)图像在相同像素点的算术平均值,根据式(9),光源随机波动度kw=±1.4%,光源漂移系数kr=-0.03%/min。由于校准实验中单帧曝光时间为ms级,且光源在控温期间处于关闭状态,仅在图像采集时开启,因此本文在耦合计算时忽略光源漂移的影响。

图5 光源发光强度变化

图6为CCD的非线性测量结果,图中纵坐标为光强,横坐标为曝光时间,红点为选定像素上在不同曝光时间下测得的80帧图像的平均值,黑线为其最小二乘拟合曲线,视为理想值。由于曝光时间较短,仍不考虑光源漂移的影响。由式(10)可见,CCD的非线性噪声会受到图像帧平均数量Nimage的影响,图7为在不同曝光时间下,CCD相机在不同时刻的非线性度随图像帧平均数量的变化情况。其中图像帧平均数量为6帧时可以大幅降低由随机误差带给CCD非线性度的影响,当图像帧平均数量达到30帧以后,CCD的非线性度已经趋于稳定,此时在不同图像强度水平下,可以发现曝光时间为140 ms,即对应图像强度为10 500时,CCD非线性噪声最小,其次是与之相邻的160 ms、180 ms、120 ms和100 ms,对应图像分布在7 800～13 000之间。在这一图像强度范围内,CCD相机均在线性度良好的区间内工作,实验中应该尽可能将关注工况的TSP图像强度调整至这个范围内。由于参考工况在比处理中会作为一个固定的分母,因此建议应该在参考工况下再次微调曝光时间,使其图像强度处于10 500左右,这样可将CCD非线性对校准结果的影响降至最低。

图6 CCD非线性测量结果

图7 CCD的非线性度变化趋势

值得注意的是：在确定的入射强度下,CCD的非线性噪声本应为系统误差,即在实验阶段,可根据非线性标定结果结合高精度插值方法对测量数据进行补偿。但是在校准阶段,CCD相机在不同温度工况下接受的光强水平覆盖了较广的范围,因此本文参照式(10)计算CCD的非线性度在整个光强探测范围的标准差,取30帧平均的结果进行计算得到kn=±0.47%

根据TSP校准范例,以288 K工况为例,减去暗背景图像处理后的原始灰度图像如图8所示。图8中红框为选取的数据平均区域,包含的像素数量为363×285,平均光强为10 730。结合不同温度下的校准数据,代入式(11)可得不同温度工况下的不均匀度,其结果如图9所示。可以明显看出若不进行区域平均,相较于其他误差来源,空间不均匀性噪声从数值上看是校准系统的主要误差来源。因此,光源在校准平面的光源不均匀性需要在校准实验之前提前进行控制;此外,涂料喷涂应尽可能保证均匀。

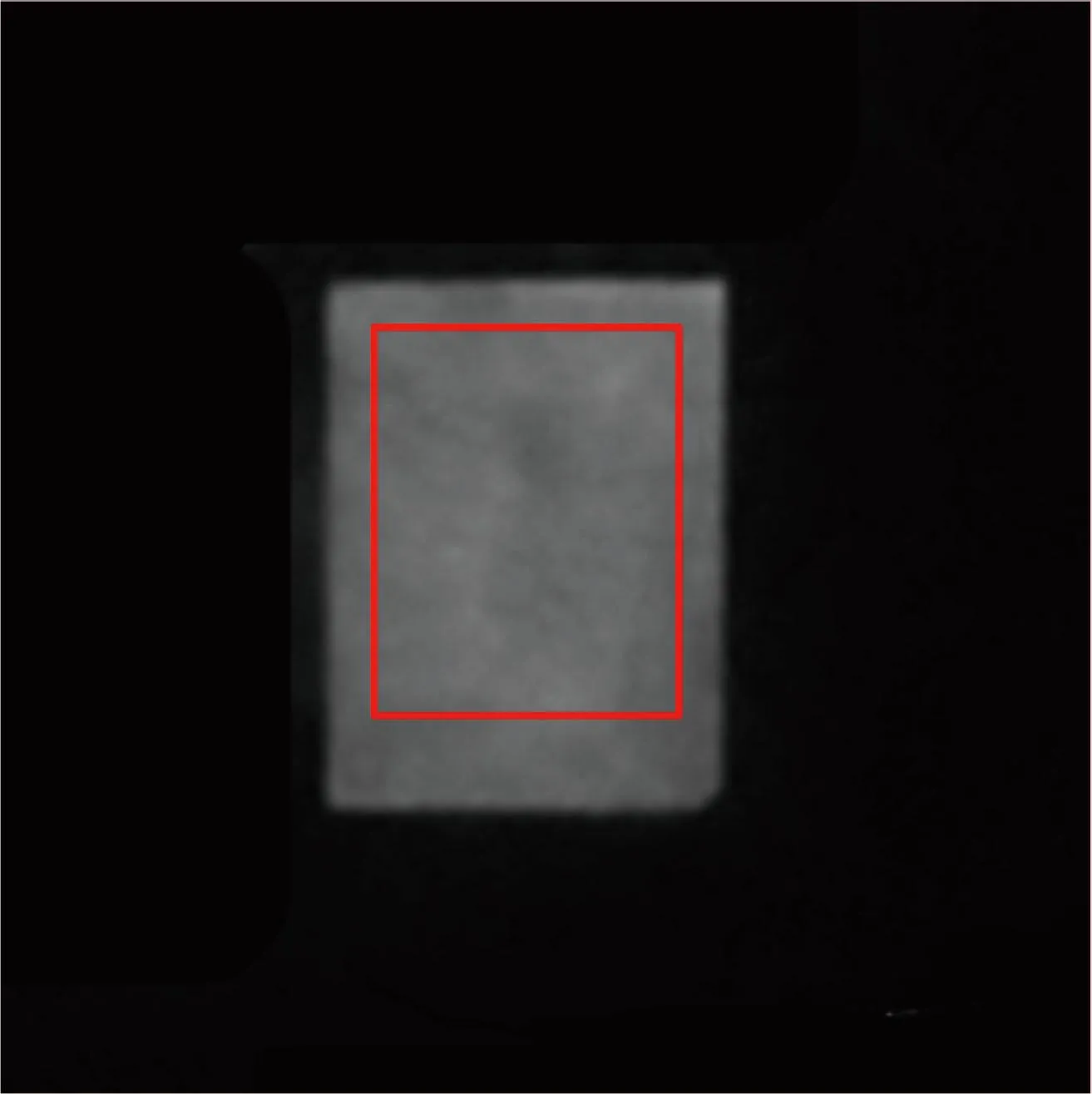
图8 288 K时的原始灰度图像

图9 不均匀度分布(区域平均处理前)

5.3 误差耦合计算结果及分析

根据各误差因素不确定度计算结果,结合式(4)和式(5),计算可得各个温度工况下所得光强比的误差δ(IT/Iref),将其进一步代入式(7)可计算得到校准曲线误差δ(IT/Iref)fit。如图10所示,结果表明在相对低温区,校准曲线的精度更低,其原因是在误差源中,大多数都与绝对光强有关,且与之成正相关,因此在发光强度较高的低温范围内,校准曲线绝对误差更大。

图10 校准曲线的光强比误差分布

图11为TSP温度灵敏度[16]计算结果。结合图9,计算可得校准曲线用于测温时的温度误差分布,计算结果如图12所示。结果表明：由校准实验造成的TSP最大测温误差小于0.4 K;整体测温误差在测温范围内呈凹形分布。

图11 TSP温度灵敏度

图12 校准曲线测温误差分布

由于最终的误差带计算结果与每个误差源的不确定度评估结果直接相关,为了证明评估过程的合理性,有必要验证误差带计算结果的准确性。理论上,通过重复性实验可以获得多条校准曲线,并通过其在每个测点的概率密度分布获得其误差范围,但这种方法在工程上是极其耗时的。为了获得更准确的误差估计,校准曲线样本的数量应尽可能多;然而,涂料在长时间运行下的性能变化是未知的。因此,本文采用了统计方法进行验证。具体操作步骤如下。

① 基于每个温度工况下采集的30帧图像的平均结果,在每个温度工况下,通过使用蒙特卡洛方法在30帧图像中各自随机采样一帧,可以获得校准所需的拟合数据。

② 对每次采样的16对数据(本文设置了16个温度条件)进行拟合,拟合形式保持不变。

③ 重复步骤①和步骤②10 000次。

上述方法在一定程度上模拟了重复实验的结果。然而,由于在每个温度工况下仅随机选择一帧图像,因此无法执行帧平均,这可能导致得到的误差带范围略大。图13为通过上述方法获得的10 000条校准曲线。以278 K为例,图14为根据校准曲线计算的该点10 000个光强比数据的分布。该分布符合正态分布,通过95%置信水平(取两倍标准偏差)获得校准曲线的误差带。误差计算结果对比如图15所示。可以看出两种方式均捕获了低温和高温区域的误差分布特征。但与统计方法所得结果相比,在总体趋势一致的情况下,本文的误差传递计算结果能够呈现更多的分布细节。

图13 蒙特卡洛方法获得的10 000条重复性校准曲线

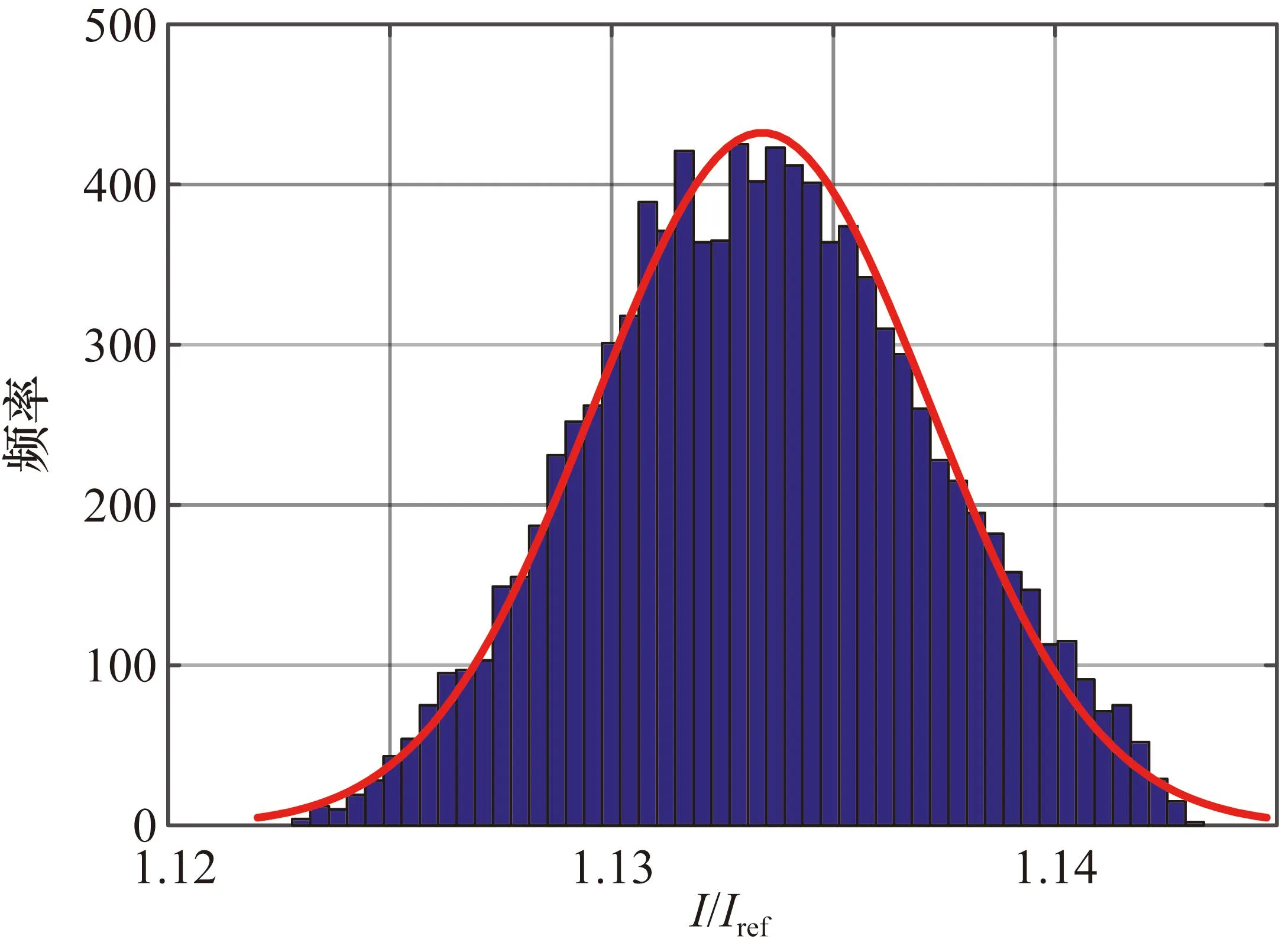
图14 278 K时的光强比数据分布

图15 误差计算结果对比

6 结论

① 本文提出的全因素误差分析方法和多误差耦合计算方法可用于有效、准确地给定校准误差范围。

② 针对某型国产TSP的校准结果表明,本文采用的TSP校准系统和数据处理方法具有较高的精度,计算结果表明,由校准实验引起的最大温度测量误差小于0.4 K。

③ 校准过程中图像帧的最佳平均数约为30帧,在保证光源照射均匀性的条件下,应尽可能增加区域平均中使用的像素数。在吹风实验阶段,应根据实验成本综合考虑,最好确保6帧以上的有效图像。

值得注意的是,虽然误差源的数量并不会影响本文提出的校准误差耦合计算方法。但是在结合具体校准实验时,本文中考虑的误差源可能并不是详尽的,需要进一步结合具体的校准系统组成和所采用的校准流程对其进行增减。