阶梯式碳税下煤炭海铁联运网络调运优化研究

刘国跃，王长宝，刘志江，王金刚，张海龙，李 宁

（1.国家能源投资集团有限责任公司，北京 100011；2.南瑞集团有限公司 国网电力科学研究院有限公司，江苏 南京 211106）

0 引言

我国煤炭资源总体呈现北多南少、西多东少的分布形式，而我国煤炭的主要需求单位火力发电厂，除部分分布于内陆铁路沿线的主要城市外，大部分分布于东南沿海等发达地区，这导致我国长距离煤炭运输需求旺盛。考虑到我国东南沿海地区航运系统发达，且长距离铁路运输与航运相比成本高且运量小，因此海铁联运是目前我国主要的煤炭运输方式之一。传统的海铁联运调运方案决策仅考虑运量及运输成本，而在国家深化交通运输供给侧结构性改革，以及实现“碳达峰”“碳中和”目标的背景下，低碳海铁联运煤炭运输的研究具有重要的理论和现实意义[1]。近年来的文献中有较多低碳多式联运路径优化方面的研究。李珺等[2]将运输时间、中转时间、客户需求和中转集拼货运量设定为四重混合不确定因素，通过分析受不确定因素影响下的多式联运成本，进行多式联运路径规划。邓学平、梅梦婷等[3-4]均采用三角模糊数表示多式联运路径优化问题中的不确定需求和不确定时间，不同的是，邓学平采用机会约束规划理论将不确定模型确定化，梅梦婷则是构建考虑碳排放的多目标模型并采用多目标算法求解。袁旭梅等[5]将不确定的货运需求表示为区间数形式，并基于此构建多式联运路径鲁棒优化模型，并且分析了不同的碳排放政策对模型的影响。Zhang 等[6]针对低碳多式联运路径优化问题，设计了混合鲁棒随机优化模型，并分别针对运输模式、货运需求和运输时间不确定场景下的模型及算法的有效性进行了分析。Jiang 等[7]研究了城市群发展背景下具有二氧化碳减排目标和需求不确定特点的区域多式联运物流网络设计问题。蒋琦玮等[8]在时间不确定的条件下，针对集装箱多式联运路径优化问题，将碳排放成本内化为总成本，并研究了税率变化对成本的影响。张旭等[9]将碳交易价格考虑为不确定条件，建立多式联运路径混合鲁棒随机优化模型。刘松、Zhao 等[10-11]分别研究了碳排放限制条件下的冷藏集装箱和普通集装箱多式联运路径优化问题。从以上研究可以看出，在进行多式联运路径优化研究时碳排放是一项非常重要的影响因素，有的研究是将碳排放内化为总成本的组成部分，有的分析对比了不同的碳排放政策对路径优化结果的影响。然而，对于碳排放价格的刻画，这些研究采用的都是固定费率的碳交易价格或者碳税。相关针对不同碳排放政策间替代效应的研究结果表明，就目前的实际情况来看，碳排放权交易价格往往过低，对促进碳减排的效果差强人意，而碳税的加入恰好能弥补这一不足。翁智雄等[12]通过设定不同的税率测算出2020 年的碳减排效果，发现税率越高，碳减排效果越好。王金南等[13]基于可计算一般均衡模型(Computable General Equilibrium，CGE)开发的能源政策综合评价模型——能源经济模型，针对低、中、高3 种碳税税率对我国国民经济、能源消费及碳减排的影响进行了情景模拟，提出宜在2012 年按中等税率(20 元/t)征收碳税，并认为税率应呈阶梯式上升。姚昕等[14]采用动态DICE 模型，研究发现我国最优碳税额度随时间推移而逐步上升，由2008 年的7.31 元/t 上升至2020 年的57.61 元/t。因此可以看出，在合理阶梯高度范围内，阶梯式碳税相较于固定碳交易价格和碳税相比，对企业的碳减排有明显的促进作用。而一旦阶梯式碳税的阶梯过高，会有增加政策阻力风险[15]。因此，为了探索更为合理的碳排放政策形式，在多式联运运输方案制定过程中引入阶梯式碳税具有重要的现实意义。

同时，针对煤炭运输优化问题，Gupta 等[16]基于层次分析法和数据包络分析技术构建多目标优化模型，同时优化采矿业车辆运输路线和类型的选择。Li 等[17]构建了一个涵盖我国30 个省级行政区域的能源系统模型，分析了省际煤炭运输的碳排放量，同时预测了不同碳减排政策场景下各地区煤炭运输污染排放的变化趋势。Liu等[18]以煤种、煤质、运输条件等因素为评价依据构建煤炭供需匹配度评价体系，进而构建以匹配程度最大和营业额最小为目标的煤炭运输分配优化模型。郭波等[19]考虑包括铁路货运通道规划造价成本在内的区域全局运输成本，提出了一种煤炭铁水联运运输通道规划方法。以上针对多式联运低碳化转型和煤炭运输优化的研究大多是针对路径优化的研究，即多式联运运输方式的选择，其模型中会考虑单次运输的运量以计算运输成本及碳排放量，却没有考虑运输线路的运输能力和线路间的运力平衡。尤其是在铁路运输段，实际运营过程中各区间运输能力有着严格限制，若不考虑可行路径间的运力平衡，一旦超出限制将面临运输方案无法实施的后果。因此，在海铁联运网络的建模中，将着重考虑铁路区间运能限制和煤炭港口的吞吐量限制，以确保调运方案在实际运营过程中切实可行。

综上所述，研究在大规模海铁联运网络背景下，考虑煤矿与电厂间供需平衡约束和铁路与港口的运输能力限制约束，同时引入阶梯式碳税策略，构建海铁联运煤炭调运方案非线性优化模型，并针对模型特征设计一种组合式算法(Combinatorial Algorithm，CA)对模型进行求解，该算法分为内外2 层迭代算法，外层迭代算法采用增广拉格朗日乘子法，内层迭代算法采用可行方向法。最后，通过算例分析验证模型和算法的有效性，并比较固定碳税和阶梯式碳税策略下的煤炭调运方案碳排放量变化趋势。

1 问题描述及符号定义

1.1 问题描述

煤炭由煤矿开采出后，经过短驳运输到达对应铁路装车站。经装车站装车后，煤炭正式进入海铁联运网络开始运输。装车后的煤炭分为2 类去向，一是经过铁路运输至沿线各电厂卸车，完成煤炭运输，称为直达煤；二是运往各煤炭转运港，准备进行第二阶段的航运运输，称为下水煤。下水煤经由港口转运后，由货运船舶运输至东南沿海各电厂，进而完成煤炭海铁联运过程。直达煤的运输会占用铁路运输能力，从而影响下水煤的调运量。煤炭海铁联运网络示意图如图1所示。

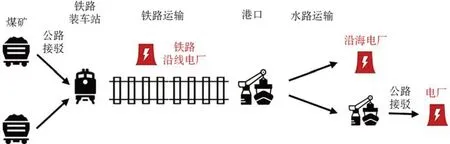
图1 煤炭海铁联运网络示意图Fig.1 Sea-rail intermodal transportation network for coal transport

因此，研究的问题是在考虑线路运能约束和阶梯式碳税的条件下，寻找满足煤矿和电厂煤炭供需平衡要求且煤炭生产企业总效益最大化的煤炭联运路径方案及各条路径上的年运输煤炭总量。

1.2 海铁联运网络符号定义

G(N，L) 表示海铁联运网络， 其中N={ni，nj，nq，ng}表示网络中运输节点集合，由装车站、电厂、港口和其他节点组成，ni={ni1，ni2，…}表示装车站集合，nj={nj1，nj2，…}表示电厂集合，nq={nq1，nq2，…}表示港口集合，ng={ng1，ng2，…}表示除装车站、电厂、港口之外的网络节点。L={ln1，n2|n1，n2∈N}表示煤炭海铁联运网络路段集合(相邻节点)，其中ln1，n2表示相邻节点n1和n2之间的路段，因航运线路中间不经过其他港口，故其ln1，n2即表示由北方出发港到东南沿海到达港的整体路段。

1.3 阶梯式碳税

阶梯式碳税是指税率随着碳排放量的增加而呈现阶梯式增高[15]。

阶梯式碳税的阶梯高度为相邻税率之间的差值，则阶梯高度Δf(ρ)和碳税T(ρ)为

式中：ρ为除去初始碳配额外需要支付碳税的碳排放量；α为能源企业初始碳配额，t。

考虑到以上阶梯式碳税为分段函数，导致在模型求解时需要先判断碳排放量所处区间。因此，为求解方便，这里将阶梯式碳税的区间取极限处理，即lim Δρ→0，使得碳税的阶梯式趋于递进式，碳税的税率函数趋于连续的函数。

lim Δρ→0条件下的碳税T(ρ)公式如下。

取极限处理的阶梯式碳税如图2所示。

图2 取极限处理的阶梯式碳税Fig.2 Tiered carbon tax treated by limits

如图2 所示，求极限之前的原始阶梯型碳税呈离散形势分布，并且随着碳排放量的升高，Δf(ρ)也会逐渐增加，而求极限之后的阶梯式碳税则呈连续分布，并随着碳排放量的增加，碳税曲线的斜率越来越大。当离散型阶梯式碳税转化为连续性阶梯式碳税后，会出现一定程度的碳税变化，如图2 阴影部分所示，当碳排放越大并且越靠近离散型碳税区间边缘时，2 种方式的碳税差异越大。但是，如果采用离散型碳税，就需要对每一条运输记录的碳排放量进行识别分类并累加碳税，这将极大地增加运算的时间和复杂度。因此，研究选择采用连续型阶梯式碳税，采用公式⑶计算碳税。

2 阶梯式碳税下煤炭海铁联运网络调运优化模型

2.1 模型假设条件

（1）模型优化范围由煤炭在装车站装车开始至船舶到达电厂结束。

（2）每个煤矿仅对应一个装车站，但一个装车站可对应多个煤矿。每个电厂仅对应一个港口，但一个港口可对应多个电厂。

（3）模型仅计算大宗煤种的年运输总量，不考虑价格差异较大的特种煤。

（4）只在港口进行运输方式的转换，且至多进行一次运输方式的转换。

（5）在运输过程中，煤炭的属性状态不发生变化，没有货损情况。

2.2 模型参数及变量定义

（1）海铁联运网络参数。Ai表示装车站ni对应煤矿年可装车煤炭总量，t；Bj表示电厂nj年煤炭需求，t；ci表示装车站ni对应煤矿年平均生产成本，元/t；pj表示电厂nj购买煤炭年平均售价，元/t；cq表示港口nq的平均转运成本，元/t；pln1，n2表示铁路区间或航线ln1，n2单位里程单位重量煤炭平均运价，包括铁路运价和船舶运价，元/t；sln1，n2表示铁路区间或航线ln1，n2的长度，km；dq表示港口nq年煤炭吞吐量上限，t；dln1，n2表示铁路区间或航线ln1，n2年运能上限，t；λ表示煤矿生产煤炭总量低于电厂需求时，需求满足比例。

（2）可行路径属性参数。因网络中包含铁路沿线电厂和东南沿海电厂2 类目的地，故模型中可行路径也包括2 类：①a 路径——煤矿→装车站→铁路沿线电厂；②b 路径——煤矿→装车站→港口→东南沿海港口→东南沿海电厂。其中a 路径虽然不采用海铁联运，但是其运输会占用海铁联运中铁路段的运能，因此需综合考虑。设集合R=为煤炭生产点到销售区域的全部可行路径集合，其中，表示从ni到nj的第k条可行路径。设0-1 变量表示路径是否以装车站ni为起始点，是为1，否则为0。设0-1 变量表示路径是否以电厂nj为终到点，是为1，否则为0。设0-1变量表示路径是否经过路段，是为1，否则为0；设0-1 变量表示路径是否经过港口nq，是为1，否则为0。

（3）决策变量。设决策变量，表示路径上的年煤炭运输总量，t。

2.3 目标函数

煤炭海铁联运调运模型是以能源企业煤炭业务总效益最大化为目标。其中，利润部分由煤矿向电厂售卖煤炭所得组成，能源企业煤炭业务成本包括煤矿生产成本、铁路运输成本、船舶运输成本、港口转运成本和碳排放成本。

对于碳排放成本，以引入阶梯式碳税下的碳排放成本函数进行表示。此处令α为能源企业初始碳配额，t；θln1，n2为在铁路区间或航线ln1，n2上运输1 t煤炭的单位碳排放量，kg/(t·km)；ρ为除去初始碳配额外需要支付碳税的碳排放量。

为求解方便，这里将阶梯式碳税的区间取极限处理，即lim Δρ→0，则该条件下，碳税T(ρ)公式如下。

公式⑷表示煤矿售煤所得总利润，元；公式⑸至公式⑺和公式⑼为能源企业煤炭业务成本，元；公式⑸为煤矿生产成本，元；公式⑹为铁路运输和船舶运输总成本；公式⑺为港口转运成本；公式⑼为阶梯式碳排放成本，元。

因此，该模型的总目标函数可以表示为

2.4 约束条件

煤炭海铁联运调运方案必须满足生产-需求约束和运输能力约束。

公式⑾和公式⑿为生产-需求约束，即各煤矿运出的煤炭总量必须符合煤矿的煤炭供应能力，同时运到各电厂的煤炭也必须满足各电厂的需求。公式⒀和公式⒁为运输能力约束，即在铁路运输部分各区间的煤炭运输总量不能超过铁路区间的运输能力，到达港口的煤炭量也不能超过港口的最大年吞吐量。公式⒂为决策变量非负约束。

3 模型分析与内外双层迭代算法设计

研究所构建的模型引入了阶梯式碳税来量化碳排放成本，但由于阶梯式碳税在目标函数中为积分形式，因此模型从原不考虑碳税的线性规划模型转变为了带有路段和港口能力限制约束的非线性规划模型。因此，每条可行路径上分配的调运量由铁路区间通行能力约束、港口吞吐量约束和随碳排放量呈非线性递增的阶梯式碳税共同影响决定。

首先，[M 1]原模型转化为最小化形式

上述模型是一个非线性优化模型，针对该模型特性，本研究设计了一个组合式求解算法，该算法包含内外双层迭代算法，外层算法以增广拉格朗日乘子法为基础进行设计，将铁路区间通行能力和港口吞吐量限制约束作为拉格朗日乘子项，构建增广拉格朗日函数。然后，采用可行方向法作为内层迭代算法，将外层算法得到的非线性目标函数线性化。

3.1 外层迭代算法

外层迭代算法采用增广拉格朗日乘子法，将铁路区间通行能力约束和港口吞吐量约束作为拉格朗日乘子项，放入目标函数中，并在拉格朗日函数中增加了一项惩罚函数，从而构建海铁联运增广拉格朗日目标函数。外层迭代算法的求解思路如下。

首先，在公式⒄和公式⒅中，令

再通过添加松弛变量，将不等公式⒄和公式⒅转化为等式形式，得到转化后的等式为

式中：和sq为松弛变量向量。

目标函数的增广拉格朗日函数表达式为

式中：μln1，n2，μq为拉格朗日乘子向量，其维数分别与L元素个数和nq元素个数相等；γ为惩罚参数。

从而，[M 1]可以转化为求解以下问题。

由于[M 2]包含多个变量，因此可对[M 2]分步求最小化。对给定x，首先求sln1，n2和sq的最小值，然后再求x的最小值。

通过对sln1，n2和sq求最小值，可以得到

接下来，假设当前迭代点为和，通过求解[M 3]，得到x(k)。[M 3]的求解步骤见下一节内层迭代算法。此时惩罚参数和拉格朗日乘子可更新如下。

此处惩罚参数更新时的扩张因子取1<κ≤2，该范围可以避免内层算法在求解子问题时发生病态，无法得到最优解。

3.2 内层迭代算法

内层迭代算法是用以求解外层算法在和条件下的子问题[M 3]，即在海铁联运调运优化问题中每一次外层迭代，都需要求解[M 3]。

[M 3]是一个仅含有等式及非负约束的非线性优化子问题，因此求解该模型可以通过将目标函数线性化，转化为求解线性规划子问题，从而得到目标函数的可行下降方向，这也正是可行方向法的基本思想。

内层迭代算法具体思路如下：假设当前迭代点为x(τ)，在该点将[M 3]目标函数线性化，得到以下子问题。

假设为上述子问题的解，则可行下降方向为

沿该方向进行一维搜索，即通过求解

得到最优步长λ，则下一个迭代点为

为得到y(τ)，需要求解[M 4]。[M 4]可表示为

通过上述推导过程可以看出，通过将[M 3]的目标函数线性化，所得到的子问题[M 4]，恰巧是一个标准的Hitchcock 问题。因此其可运用现有Hitchcock问题求解算法[20-23]快速求解。

CA流程图如图3所示。

4 案例研究

4.1 案例背景

以国家能源投资集团有限责任公司(以下简称“国家能源集团”)煤炭海铁联运网络为例，采用其煤炭业务相关数据作为参数，构建煤炭能源企业海铁联运调运方案优化模型，内层迭代算法Hitchcock模型采用Gurobi进行求解。国家能源集团海铁联运网络示意图如图4所示。

图4 国家能源集团海铁联运网络示意图Fig.4 Sea-rail intermodal transportation network in the China Energy Investment Group Co., Ltd

该网络中参与煤炭生产、装卸、运输的节点一共有188 个，其中煤炭装车站47 个，电厂33 个，港口8 个，其余为其他车站。煤炭矿区集中在西北地区，因此装车站也集中分布于西北地区，在铁路运输部分，煤炭由西向东进行运输，在航运部分，煤炭由北向南运输。根据节点的邻接矩阵可以得到网络中从任一生产节点到任一销售区域共有7 134条可行路径。将7 134 条可行路径进行编号，编号为No.0~No.7133。初始化最短可行路径集R(0)选取85 条路径，初始可行路径集中部分可行路径信息如表1所示。

表1 初始可行路径集中部分可行路径信息Tab.1 Partial feasible path information in initial feasible path set

4.2 计算过程及结果

对于阶梯式碳税价格区间的设定，张济建等[15]对既有研究中针对我国碳税政策发展趋势和合理价格区间的研究进行了总结和探讨。其研究结果表明，将碳税税率设定在29~73 元/t 之间波动更符合我国的经济发展和碳排放现状。根据《中国能源统计年鉴2018》中能源消耗量折算为碳排放量的结果，铁路运输的单位碳排放按照0.035 kg/(t·km)，航运碳排放按照0.101 kg/(t·km)计算[24]。R(0)条件下进行各OD 对的调运量加载，生成初始方案，其总企业效益为-1.610 8×1011元。再进行第二次迭代，煤炭调运方案的总企业效益为1.318 3×1010元。再进行第三次迭代，生成新调运方案总效益为1.704 4×1010元。然后，方案满足收敛性判断条件，因此算法终止，1.704 4×1010元即为该问题的最优解。

为验证设计的CA 在求解质量和效率方面具有良好的性能，算例直接在包含7 134 条的全可行路径集条件下，采用遗传算法(Genetic Algorithm，GA)对原始非线性规划模型进行求解，得到不同算法结果对比图如图5 所示，不同算法的求解时间如表2所示。

表2 不同算法的求解时间sTab.2 Solution time of different algorithms

图5 不同算法结果对比图Fig.5 Comparison of different algorithm results

由图5可以看出，GA随机生成的初始种群最优解是-2.975×1011元，而CA在条件下生成的初始方案为-1.610 8×1011元，相较于GA 提升了45.9%。GA 收敛后的最优解为8.765×109元，而CA 满足收敛条件后的最优解为1.704 4×1010元，相较于GA提升了94.5%。在收敛性方面，GA在迭代323次后收敛，而CA 仅迭代3 次即满足收敛性判断条件，但是由于所设计的CA 为启发式算法，GA 为元启发式算法，因此两者的收敛次数不具有可比性。

虽然收敛性不具有可比性，但是收敛时间仍能够表明算法的求解效率。由表2 可以看出，CA 相较于GA在求解效率方面提升了69.8%。

综上所述，所设计的CA 针对煤炭能源企业海铁联运调运方案优化模型的求解，不论在初始解的生成、最优解的质量和求解效率方面都明显优于GA，证明CA在求解质量和效率方面均具有更好的性能。

4.3 不同碳排放政策下的敏感性分析

为对比固定碳税和阶梯式碳税对煤炭海铁联运方案企业效益和减排效果的影响，验证阶梯式碳税相较于固定碳税的优势，根据文献[15]对相关碳税研究的归纳总结，在0~200 元/t 的范围上分别对采用固定碳税政策和阶梯式碳税政策进行敏感性分析。在固定式碳税敏感性分析中，碳税的取值由0元/t向200元/t逐渐增加，在阶梯式碳税中，碳税取值为区间形式，上限由0 元/t 向200 元/t 逐渐增加，下限则根据上限取值，遍历所有合理范围内的取值。固定碳税敏感性分析结果如图6所示，阶梯式碳税敏感性分析结果(a)如图7所示，阶梯式碳税敏感性分析结果(b)如图8所示。

图6 固定碳税敏感性分析结果Fig.6 Sensitivity analysis results of fixed carbon tax

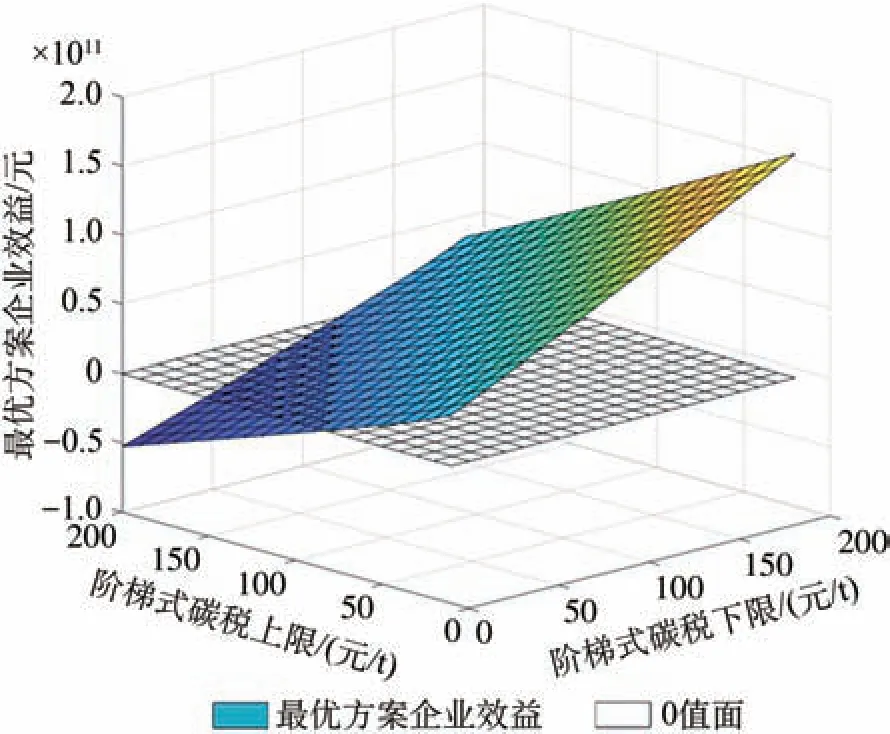
图7 阶梯式碳税敏感性分析结果(a)Fig.7 Sensitivity analysis results of tiered carbon tax (a)

图8 阶梯式碳税敏感性分析结果(b)Fig.8 Sensitivity analysis results of tiered carbon tax (b)

在图6 中，固定式碳税在由0 元/t 向200 元/t 逐步增加时，最优方案的企业效益逐步降低，但最优方案的总碳排放量不变。因为当碳税的税率固定不变时，根据碳排放量的计算方法，总碳排放量与各方案的运输距离和货运量相关。这导致固定碳税在模型目标中表述为一次项，相当于在原决策变量的系数中增加了一项成本系数，不会对最优方案的路径选择产生影响。在目前政策实行过程中，大多使用固定式碳税，由于其计算方式简单，政策实行方便。但是固定式碳税的实施更多地会导致政策“一刀切”的后果，运输企业会在保证货运量不变的情况下涌向最短路径，这虽然能够减少总碳排放量，但是不利于海铁联运网络的整体均衡发展。相较之下，阶梯式碳税的灵活性能够在促进货运企业减少碳排放的情况下，促进海铁联运网络的发展。

图7 为阶梯式碳税的上限和下限由0元/t向200元/t逐步增加时的最优方案企业效益，这一敏感性分析指标旨在探究阶梯式碳税区间变化对企业减排积极性的影响。可以看到，当碳税下限小于110、碳税上限大于90 时，会出现最优企业效益小于0 的情况。这与既有研究得到的不适宜的阶梯式碳税税率和梯度会使企业利益受损，打击企业减排积极性[15]的结论相吻合。

图8为阶梯式碳税的上限和下限由0元/t向200元/t逐步增加时最优方案的总碳排放量，这一敏感性分析指标旨在探究阶梯式碳税区间变化对减排效果的影响。可以看到，当阶梯式碳税的上限逐步减小，下限逐步升高时，最优方案的总碳排放量在逐渐减少。这说明，在一定程度上减小阶梯式碳税上限和下限之间的差距，能够提升碳税的减排效果。

结合图7 和图8 可以得到，当阶梯式碳税下限逐渐上升，上限逐渐下降时，该碳税下的最优调运方案的企业效益和减排效果均呈上升趋势，其结果将优于相同条件下采用固定碳税得到的最优方案的企业效益和减排效果。

5 结论

通过对阶梯式碳税下煤炭海铁联运网络调运优化问题的研究，得到结论如下。

（1）煤炭海铁联运网络调运优化模型可以在考虑铁路与港口运输能力约束的基础上，有效地实现能源企业与电厂间的供需关系平衡，并在以企业总效益最大化为目标的基础上，促进和提升调运方案减排效果。

（2）所设计的CA 能够满足大规模海铁联运网络的现实场景需求，能够达到较高的求解质量。

（3）阶梯式碳税相较于固定碳税更适用于我国煤炭海铁联运场景，能够在保证货运企业效益的前提下，促进货运企业的碳减排效果，同时保障海铁联运网络货运通道的均衡建设和发展。

（4）国家相关部门在制定碳税政策时，需考虑阶梯式碳税的合理上下限和阶梯高度，以求在保证能源企业生产效益的基础上实现节能减排效果的最大化。根据我国碳排放现状和相关敏感性分析结果，研究建议国家相关部门针对国家能源集团的阶梯式碳税区间定为29~73元/t。