基于累加式实时串并联变换算法的机械故障声学监测方法*
祝洲杰,杨金林,毛鹏峰
(1.浙江机电职业技术学院 智能制造学院,浙江 杭州 310053;2.浙江理工大学 机械工程学院,浙江 杭州 310018;3.中杭监测技术研究院有限公司,浙江 杭州 310022)
0 引 言
物联网(IoT)是实现工业4.0的关键技术,其可以大幅提高工业效率[1],其中典型的应用之一就是基于物联网的故障监测[2],可有效避免机械故障造成的严重损害。
故障监测[3]通常是通过监测机械振动以及机油量、温度等来实现的。声音是由机械振动引起的,因此,声音会根据机械状态的变化而变化。人工声学监测不需要在机器表面放置任何传感器或电极,可以避免传感器掉落带来的安全隐患。有经验的一线工人仅需听声音就能够判断机器故障。然而,机械故障声学监测不应该仅依赖于人工的经验或直觉来实现。
目前,基于声发射信号的机械故障监测技术大致可分为两类:1)基于机器学习的方法;2)无需机器学习的方法。
基于机器学习的方法主要是使用神经网络、支持向量机、深度学习等机器学习技术,对声发射信号进行更精确和自动化的故障监测。例如,PHAM M T等人[4]提出了利用深度生成对抗神经网络和声发射信号二维的表示,来进行滚动轴承的故障诊断。彭威等人[5]提出了利用声发射信号来提取机械转子运行状态的特征图谱,并结合卷积神经网络(convolutional neural networks,CNN)来提高机械转子碰摩擦故障识别的精度。但是,在实际应用中,采用上述方法很难收集神经网络所需的大量训练数据。
无需机器学习的方法主要是采用阈值检测法、统计分析、特征提取和匹配等方法,以此来实现机械故障监测目的。相比基于机器学习的方法,此类方法的精确度较低,但实时性较好,无需机器学习模型的训练过程。例如,刘少康等人[6]提出了一种基于改进局部均值分解的机械声学监测方法,其采用二分法分割了声音信号中的时频和幅度成分,并通过权重策略和掩膜信号来实现对齿轮箱复合故障的预测目的。李静娇等人[7]提出了一种基于Morlet小波变换的轴承声学监测方法,该方法能有效地从强噪声背景中提取出轴承声学故障的信号。
采用无需机器学习技术的方法时,为了获得实时性,必须对声音的时频域信号进行处理,因此需要使用短时傅立叶变换(short-time Fourier transform,STFT)[8]或者小波变换[9],这会导致两个问题:1)STFT不适合分析低频信号,需要大量的信号样本才能提高低频带的识别精度[10],这不仅需要大量的内存和计算量,而且捕获信号样本的时间也很长;2)小波变换虽然能够更好地处理低频信号,但是计算复杂度较高。
然而事实上,在物联网场景中,低计算量和低频特征识别是很重要的,特别是对冲压机床的故障监测[11],其低频信号经常包含了与机械故障相关的显著信息。
因此,为了降低冲压机床故障监测的计算复杂度,并提高低频识别精度,笔者提出一种机械故障声学监测方法。
首先,笔者针对频率轴上多个周期信号重叠导致参数估计较为困难的问题,提出一种累加式实时串并联变换算法;然后,通过样本时隙划分,将累加式实时串并联变换算法应用于机械故障监测,并通过仿真和实际冲压机床实验,验证累加式实时串并联变换算法在机械声学监测中的可行性;最后,详细分析累加式实时串并联变换算法的计算复杂度,并将其与Morlet小波变换进行对比。
1 研究目的
目前,冲压机床已经被广泛应用于各种工厂中,用于将金属板材或带材压制成各种零件或产品。
冲压机床的机械故障主要有两个[12]:1)大齿轮断齿;2)曲轴滑动磨损。由于大齿轮和曲轴的运动非常缓慢,通常一次冲程大约需要几秒钟,因此,这两个问题主要表征在声音的低频段。
目前还没有关于机械声学低频分析的研究。因此,笔者试图检测大修前后冲压机床的声学信号的变化,从而解决其声学监测问题。
笔者在声学监测方面提出两点建议:
1)在不依赖于人工经验或直觉的情况下,定量地区分正常状态和异常状态下机械声音信号的差异;
2)声学分析不应采用机器学习技术。这是因为这种技术在许多情况下都需要大量的训练数据,导致时间成本较大。
在接下来的章节中,笔者将采用累加式实时串并联变换算法进行声学分析,以此来验证上述两点。
2 声学信号表达式
设x(t)为麦克风采集到的输出声音信号,并以采样周期TS进行采样,如下所示:
x[k]=x(kTS)
(1)
式中:k为整数离散时间索引。
采样后的声音信号如下所示:
x[k]=s[k]+η[k]
(2)
式中:s[k]为原始声音;η[k]为噪声。
假设声音s[k]包含多个周期波形,则有:
(3)
(4)

2 机械声学监测
2.1 累加式实时串并联变换算法
由于低频信号在频率轴上容易出现多个周期信号重叠,导致利用STFT进行参数估计较为困难。因此,笔者提出了一种累加式实时串并联变换算法。
根据经典的串并转换器(serial-to-parallel conve-rter,SPC)原理[13],假设一个周期性的采样序列被送入一个SPC,且样本序列的周期为8。如果SPC的输出端口数与输入采样序列的周期相同,均为8,则此时的输出情况如图1所示。

图1 SPC输出情况1
在情况1中,可以明显地看出SPC的输出在时间轴g上总是相同的。因此,统计过程产出的累积将变得很大。
相反,如果SPC的输出端口数是7,它不等于输入序列的周期,如图2所示。
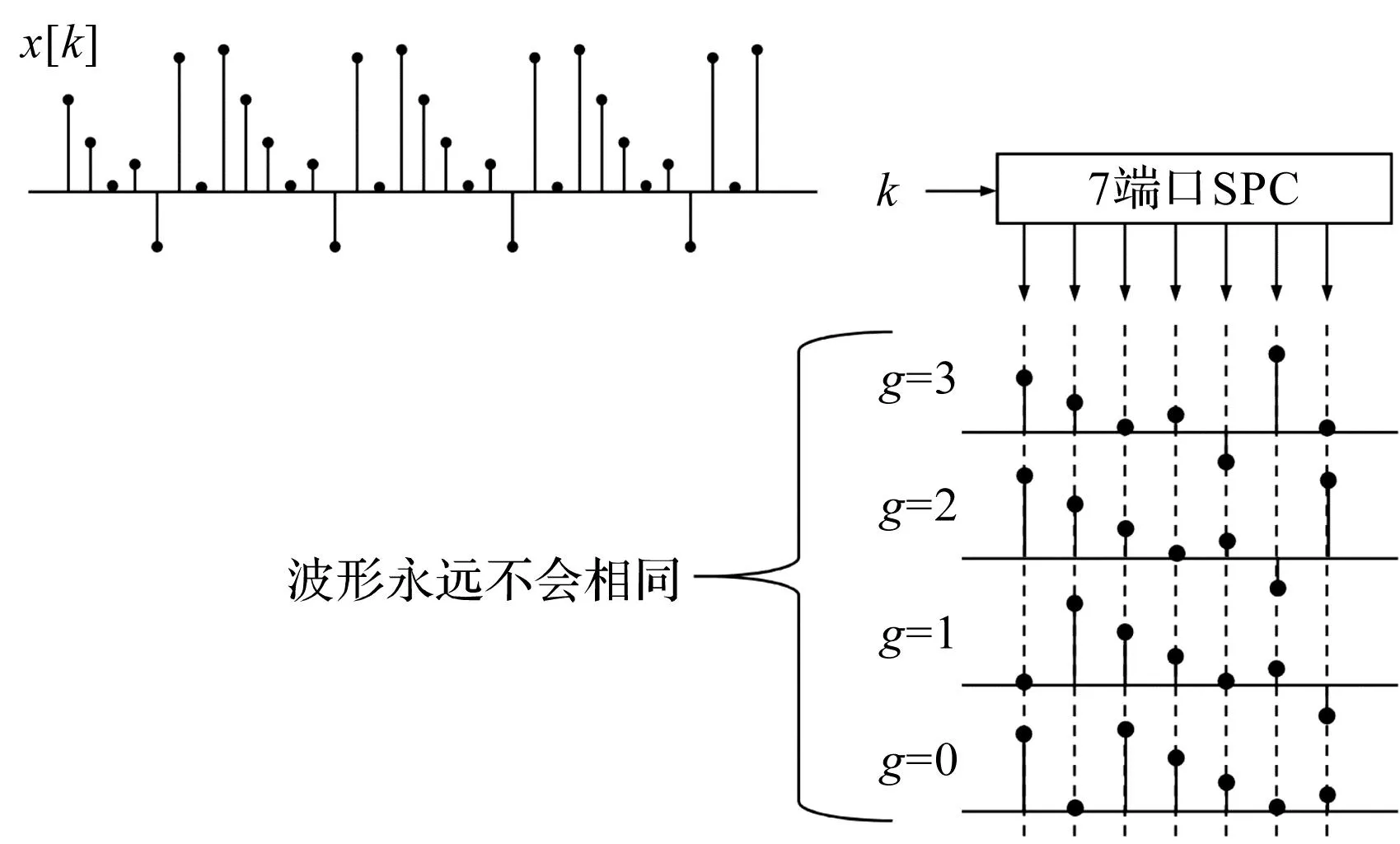
图2 SPC输出情况2
在情况2中,可以看出SPC的输出永远不会相同。因此,统计过程产出的累加将不会显著增长。
所以,笔者将多个SPC放在一起,每个SPC的输出端口的数量不同;然后将信号的采样序列并行输入到这些SPC,并在每个SPC中累加输出,比较所有SPC之间的累计输出,确定最大绝对值;在输入的采样序列s[k]中馈入多个SPC,每个SPC的输出被累加,以便从累加的波形中检测最大值;最后,对最大值进行比较。
假设有N个SPC,并由SPC #n(n=1,…,N)标识。
Mn表示SPC #n的输出端口数量,其定义如下:
Mn=Lmin+n-1
(5)
式中:Lmin为SPC #1的输出端口数。
将SPC #n的第g个(g=0,1,…,G-1)输出定义为大小为(Mn×1)的矢量xn[g],即:
(6)
SPC #n的累计公式如下:
(7)
式中:Gn为SPC #n的输出波形数。
Gn表达式为:

(8)

最后,yn实体的最大振幅如下:
(9)
式中:yn,m为yn的第m个实体。
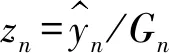
那么,zn的最大值为:
(10)
累加式实时串并联变换算法的工作原理如图3所示。

图3 累加式实时串并联变换算法的原理
2.2 在机械故障监测中的应用
在机械故障监测应用中,为了观察时变信号,笔者应用了一个短期累加式实时串并联变换,如图4所示。
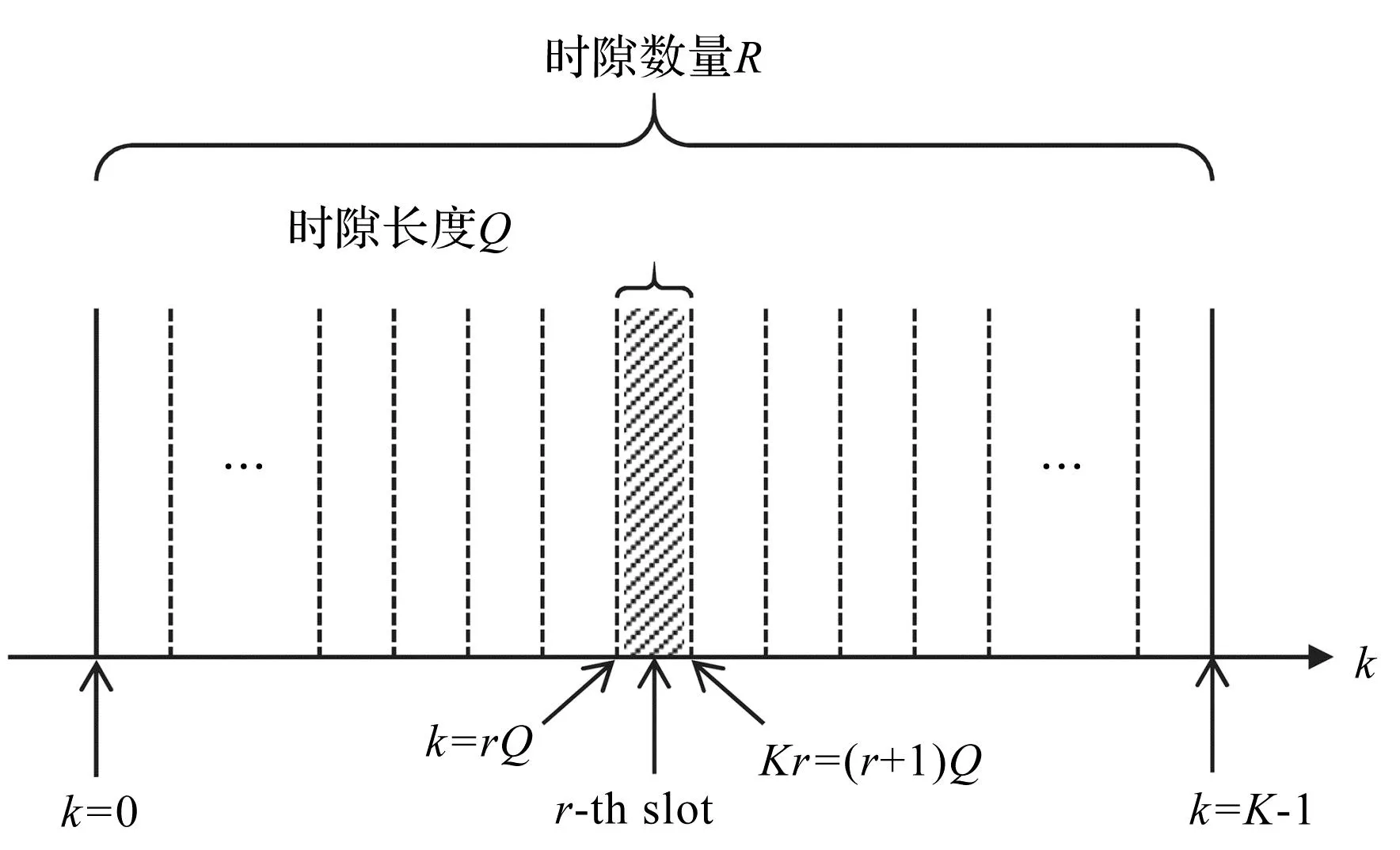
图4 短期累加式实时串并联变换
K个样本被分成R个时隙,定义如下:

(11)
式中:Q为时隙中包含的样本数,即长度。
因此,第r个(r=0,1,…R-1)时隙的第一个样本的离散时间索引k表示为:
k=rQ
(12)
而第r个时隙的最后一个样本为:
Kr=(r+1)Q
(13)
对于每个时隙,执行上节中介绍的累加式实时串并联变换。累加式实时串并联变换算法的原理与快速傅里叶变换类似[14],因此,其不适合分析非平稳信号。
冲压机床的运动是由曲轴和大齿轮的旋转产生的,相对较慢,声音信号也是周期性的和稳定的。
2.3 仿真验证
在进行实际测试之前,笔者对其进行了仿真测试,以验证累加式实时串并联变换算法的性能。
仿真参数如表1所示。

表1 仿真参数
在这个仿真中产生两个信号s1[k]和s2[k],相应的基波为φu[ku](ku=0,1,…,Tu-1,u=1,2),周期T1和T2分别为99和101。
除了周期外,两个基波的其他生成参数都是相同的,如下所示:
φu[ku]=0.95-kucosπku
(14)
笔者利用生成的基波φ1[ku]和φ2[ku],分别生成s1[k]和s2[k],并将其分布在离散的时间轴上,如图5所示。
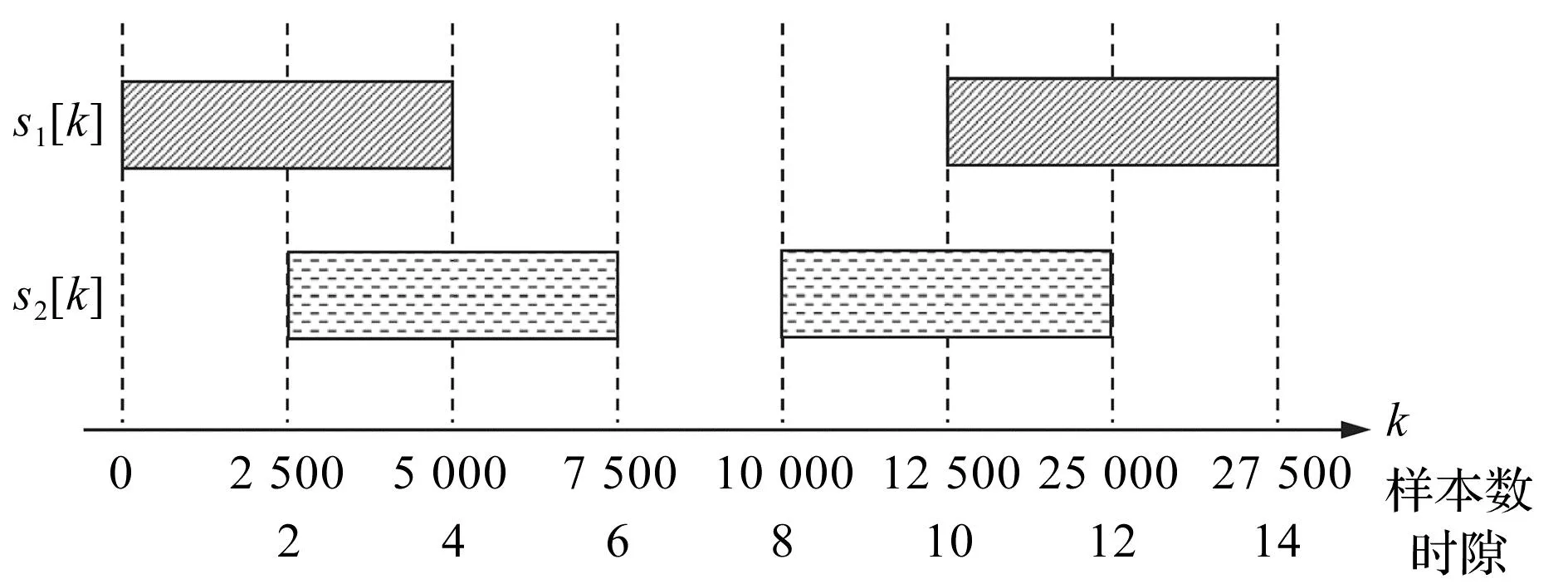
图5 离散时间轴上的信号分布
由图5可以看出:s1[k]和s2[k]在时间轴上部分地重叠了。在这种情况下,使用快速傅里叶变换或者STFT对这两个信号进行检测是非常困难的,需要大量的信号样本才能提高低频带的识别精度。
而累加式实时串并联变换算法可以清晰地显示出第r个时隙处zn(颜色条),如图6所示。

图6 仿真获得的zn
由图6可以看出:仿真结果成功检测到在图5所示的时间轴上间隔分布的s1[k]和s2[k]。
3 实验及结果分析
3.1 实验配置
笔者使用与笔记本电脑音频接口连接的麦克风,进行冲压机床的声音录制。
笔者将麦克风安装在离目标机器2 m远的地方;并在音频接口处对声音进行采样,并将其存储在笔记本电脑中,以便使用MATLAB对其进行分析。
实验系统的配置如图7所示。
实验系统中的设备参数如表2所示。

表2 设备参数
实机测试环境如图8所示。

图8 实机测试环境
笔者对机器的声音录制了三次。第一次录音是在大修之前进行的,此时机器的状态并不完美。在大修之后,立刻进行了第二次录制。在这段录音中,机器状况得到了更好的调整。为了验证其准确性,再过一周后,在相同的机器状态下又进行了第三次录制。
笔者分别使用累加式实时串并联变换算法、STFT[15]和Morlet小波变换[16]对录制的声音样本进行分析(共9次实验,待分析的样本总数设定为960 000个,采样频率设置为8 000 Hz,样本为2 min内的声音)。
累加式实时串并联变换算法和STFT的参数如表3所示。

表3 算法参数设置
3.2 实验结果分析
笔者使用累加式实时串并联变换算法、STFT和Morlet小波变换进行分析,共获得了9个实验结果。此处以第二次录制的声音为例,经过累加式实时串并联变换算法获得的zn如图9所示。

图9 获得的zn(第二次)
为了量化这9个实验所得图形结果的相似性,笔者计算了直方图的相关性。
两图形之间的直方图相关性(histogram correl-ation,HC)如图10所示。

图10 两图形之间的直方图相关性
直方图相关性RHC的计算方式[17]如下:
(15)
(16)
(17)
式中:H为直方图中bin的数量。
RHC的数值越高(接近1),则说明两图形之间的相似性越高。
9个实验所得图形结果之间的RHC如表4所示。

表4 9个实验所得图形结果之间的RHC
由表4可看出:对于累加式实时串并联变换算法,在大修后获得的第二次图形和第三次图形是相似的。与大修前获得的第一次图形相比,这两个图形的相似性较低。然而,与累加式实时串并联变换算法获得的结果相比,STFT获得的三次图形之间相关性均较低。
因此,与STFT相比,累加式实时串并联变换算法能更好地发现大修前后机器的声学特征差异。
此外,在RHC性能方面,可以观察到Morlet小波变换和累加式实时串并联变换算法是相似的,均大于0.88。然而,与Morlet小波变换相比,累加式实时串并联变换算法在第二次图形与第三次图形之间获得了更高的数值,说明在相同条件下,该方法的故障识别精度略高。
3.3 计算复杂度对比
通过对实验结果的评估,笔者阐明了Morlet小波变换和累加式实时串并联变换算法在RHC方面几乎相同的性能。
接下来,笔者将比较这两种方法的计算复杂度。
在累加式实时串并联变换算法中,对于一个时隙,加法次数由式(5)和式(8)决定,如下所示:
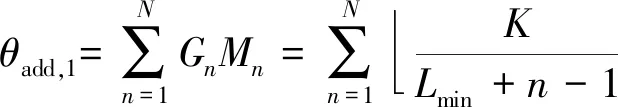
(18)
在这种情况下,K被设置为Q,因为其仅应用于一个时隙。
最终,累加式实时串并联变换算法的加法总数Θadd,1和乘法总数Θmul,1为:
Θadd,1

Θmul,1=RΘmul,1=RN=12×7 000=84 000。
在Morlet小波变换中,从0.666 7 Hz到1.600 0 Hz的带宽被分为13个子带。在每个子带中,输入样本序列x[k]与Morlet小波进行卷积。在累加式实时串并联变换算法中,利用快速傅里叶变换将卷积转换为频域中的乘法,计算复杂度会大大降低[18]。一个复数加法包含两个加数,而一个复数乘法会产生两个加数。
因此,Morlet小波变换的加法总数Θadd,2和乘法总数Θmul,2为:2Θadd,2+2Θmul,2=2(817 889 280+429 391 872)=2 494 562 304。
Morlet小波变换和累加式实时串并联变换算法的计算复杂度对比如表5所示。

表5 计算复杂度对比
由表5可以看出:尽管累加式实时串并联变换算法需要的加法总数比Morlet小波变换多2.5倍,但是乘法总数减少了20 447%,大幅减少了计算的复杂度。
4 结束语
笔者提出了一种累加式实时串并联变换算法,将输入的采样序列馈入多个输出端口数不同的串并转换器,并从累加的波形中检测出最大绝对值,并进行了比较;最后通过仿真和实际冲压机床实验,得出了如下结论:
1)不同于STFT,累加式实时串并联变换算法在仿真结果中很清楚地检测到离散时间轴上间隔分布的两个周期信号,在无需大量信号样本的情况下,这有利于提高低频带的识别精度;
2)实机测试结果表明,累加式实时串并联变换算法和Morlet小波变换的直方图相关性均高于0.88,且明显大于STFT的值;
3)尽管累加式实时串并联变换算法需要的加法总数比Morlet小波变换多2.5倍,但是乘法总数减少了20 447%,其大幅减少了计算的复杂度。
在今后的工作中,笔者将继续对累加式实时串并联变换算法进行优化,以进一步减少乘法计算量,从而有助于降低IoT监测系统的能耗。

