基于粒子-人工蜂群算法的3RPUPc-UPS并联机构运动学正解研究*
常振振,张彦斌,张 双,宋黎明,李耀光
(河南科技大学 机电工程学院,河南 洛阳 471003)
0 引 言
并联机构具有精度高、累计误差小、承载能力强、结构紧凑等特点[1-4],已被广泛应用于医疗康复、航空航天、工业生产等领域。但并联机构具有强运动耦合性,导致其运动学求解十分困难,阻碍了并联机构的推广应用。
运动学分析包括运动学逆解和运动学正解分析,是机构结构优化、性能分析和精确控制等理论研究的基础。相比于运动学逆解,并联机构的正解计算更为复杂,其求解方法包括解析法和数值法。常用的解析法有几何法[5-6]、矢量代数法[7]和四元数法[8]等,数值法有不动点迭代法和牛顿迭代法等[9]。
NAZARI A A等人[10]根据机构的几何特征,将机构的空间表达转化为平面表达,降低了运动学正解方程的复杂性。陈国旺等人[11]通过结构降耦,得到了耦合度为0的机构,并采用几何方法求解了其位置正解的显式表达。
解析法虽能求取全部运动学正解,但对耦合度高的机构,其数学推导较为繁琐。HAN Xiao-guo等人[12]采用不动点迭代法分析了6SPS机构的运动学正解,并证明该方法比牛顿迭代法更有优势。强红宾等人[13]采用调整步长牛顿法求解了Stewart并联机构的位置正解,解决了牛顿下山迭代法求解时间较长的问题。传统优化算法模型简单,但速度慢,且所求最优解一般与初始迭代点有关。
近年来,众多学者将智能算法应用于求解并联机构位置正解[14-17]。常用方法有神经网络法(neural network,NN)[18]、遗传算法(genetic algorithm,GA)[19]、粒子群算法[20]等。NN算法性能好,但需要大量的训练样本;GA算法具有可扩展性,容易与其他算法结合,但收敛速度慢、局部搜索能力差;PSO算法收敛速度快,但全局寻优性差,容易陷入局部最优解。
人工蜂群算法[21]是一种模拟自然界蜂群行为的优化算法。该算法参数设置少,对于连续函数的全局优化具有很好的搜索特性;但其后期收敛速度慢。
笔者针对新型3RPUPc-UPS并联机构的运动学特性进行研究,根据机构几何特征建立位置逆解方程,并构建出位置正解求解模型;进而提出一种基于粒子-人工蜂群算法的并联机构运动学求解方法;利用MATLAB的GUI模块开发机构运动学正解求解软件,利用算例分析,验证该算法的有效性。
1 机构的运动特性分析
1.1 机构的结构设计
新型3RPUPc-UPS并联机构的结构简图如图1所示。

图1 3RPUPc-UPS并联机构结构简图
由图1可知:动平台与定平台之间通过两种不同结构类型的支链连接。第一种支链结构类型为RPUPc(Li,i=1~3),由转动副Ri、移动副Pi、万向铰Ui和环形移动副Pci依次串联组成,并由Pci副和Ri副分别与动平台、定平台相连。
为方便表述,可以将Ui副用两个垂直相交的转动副Ri1和Ri2代替。其中,Ri副的轴线与Ri1副的轴线相互平行,并垂直于Pi副的移动方向;Ri2副的轴线在动平台平面内指向动平台圆心点Q,并与Pci副的移动方向垂直。Pci副与Ui副始终位于动平台平面内。
第二种支链结构类型为UPS(L4),由万向铰U4、移动副P4和球副S依次串联组成。将U4副用两个轴线垂直相交的转动副R41和R42表示,S副用三个轴线交于一点并两两垂直的转动副RS41、RS42和RS43表示。R41副的轴线垂直于定平台平面,R42副的轴线与RS41副的轴线分别垂直于P4副的移动方向,RS42副的轴线在动平台内并指向点Q。
Ri副与U4副均匀分布在圆心点为O,半径为R的圆OR上,Ri副轴线与圆OR相切,且R2副轴线与R1副和R3副轴线垂直。初始位置时,R2副轴线与R42副轴线平行。
1.2 机构的自由度与耦合度分析
1.2.1 自由度计算
第一种结构类型的运动支链拓扑结构记为{-Ri(⊥Pi)//Ri1(⊥Ri2)//Pci-},第二种结构类型则记为{-R41⊥R42(⊥P4)//RS41⊥RS42⊥RS43}。由于Pci副的作用效果可等效为一个转动轴与动平台中心线重合的转动副Rci,所以这两种类型支链末端构件的方位特征集[22]17-28(position and orientation characteristics,POC)分别为:
(1)
(2)
基于方位特征方程求解并联机构的自由度公式为:
(3)
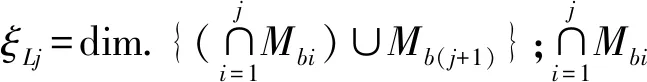
由第1、2条支链构成第一个独立回路,可得:
(4)
而第1、2条支链构成的子并联机构PM1的POC集为:
(5)
PM1与第3条分支构成第2个回路,则有:
(6)
那么,子并联机构PM2的POC集为:
(7)
同理,PM2与支链4构成第3个回路,则:
(8)
因此,并联机构的自由度和POC集分别为:
(9)
(10)
式(9)和式(10)表明:选取移动副Pi(i=1~3)的线位移和U4副中R41的转轴角位移为机构的主动输入时,该机构为四自由度三转动一移动并联机构,对应于人体腕关节掌屈/背伸、桡偏/尺偏、旋前/旋后和沿手臂方向的拉伸四种康复训练动作,可将其应用于腕关节康复训练机构。
1.2.2 耦合度计算
由基于序单开链(single open chain,SOC)的机构组成原理可知[22]107-115,任一机构可分解为若干基本运动链,独立回路数为v的基本运动链可分解为v个有序单开链SOCi(i=1~v),其中,第j个SOCj的约束度定义为:
(11)
式中:gj为第j个SOCj的运动副数;Ij为第j个SOCj的驱动副数。
机构的耦合度定义为[23]:
(12)
3RPUPc-UPS机构各有序单开链的约束度分别为:
(13)
(14)
(15)
将式(13)~式(15)代入式(12),得:
(16)
式(16)表明:该机构的耦合度为2,建立其正解解析式十分复杂[24],而求取其数值解则相对简单。
由于运动学逆解方程是构建数值解模型的理论基础,因此,需要先进行机构的逆解建模分析。
2 机构的运动学逆解分析
设Ai点为环形移动副Pci的中心点,Ci点为Ui(i=1~3)副和S副的中心点。在动平台平面内,Ai点与Ci点分别在半径为r的圆Qr和半径为c的圆Qc上。Bi点为Ri副和U4副的中心点。
笔者以定平台几何中心点O为原点,建立坐标系O-XYZ,其中,X轴与OB3重合并指向B3点,Y轴与OB4重合并指向B4点,Z轴垂直定平台平面向上。坐标系Q-xyz的坐标原点Q位于动平台几何中心,y轴与QC4重合并指向C4点,z轴垂直于动平台平面向上,x轴由右手法则确定。
2.1 逆解模型的建立
设CiBi的长度为li,即前3条支链的驱动杆长度,δ表示转轴R41的角位移(见图1),则并联机构的运动学逆解为已知动平台的位姿参数α、β、γ和z,需要求解机构主动输入线位移li和输入角位移δ。
动平台相对定平台的姿态变换矩阵可表示为:
R=Rx(α)Ry(β)Rz(γ)=
(17)
式中:Rx(α),Ry(β),Rz(γ)为动平台绕x、y和z轴的坐标变换矩阵;c*=cos*,s*=sin*。
设圆Qc上任一点CQ在xQy平面内的坐标为(x,y,0),则圆Qc在xQy平面内的方程为:
x2+y2=c2
(18)
点CQ在坐标系O-XYZ下的坐标向量CO为:
CO=RCQ+Q
(19)
式中:CQ为点CQ在Q-xyz中的坐标向量;Q为点Q在O-XYZ中的坐标向量(0,0,z)。
由于动平台绕z轴的转动不影响圆Qc在XOY平面投影的形状,将γ=0代入式(19),求点CQ在XOY平面上的投影坐标(xO,yO)为:
(20)
将式(20)代入式(18),可得圆Qc在XOY平面上投影的解析式为:
(21)
式中:t*=tan*。

(22)
(23)
设θi(i=1~3)为QCi与水平面的夹角,易知θ2=α,θ1=θ3。θ3的瞬时位形图如图2所示。
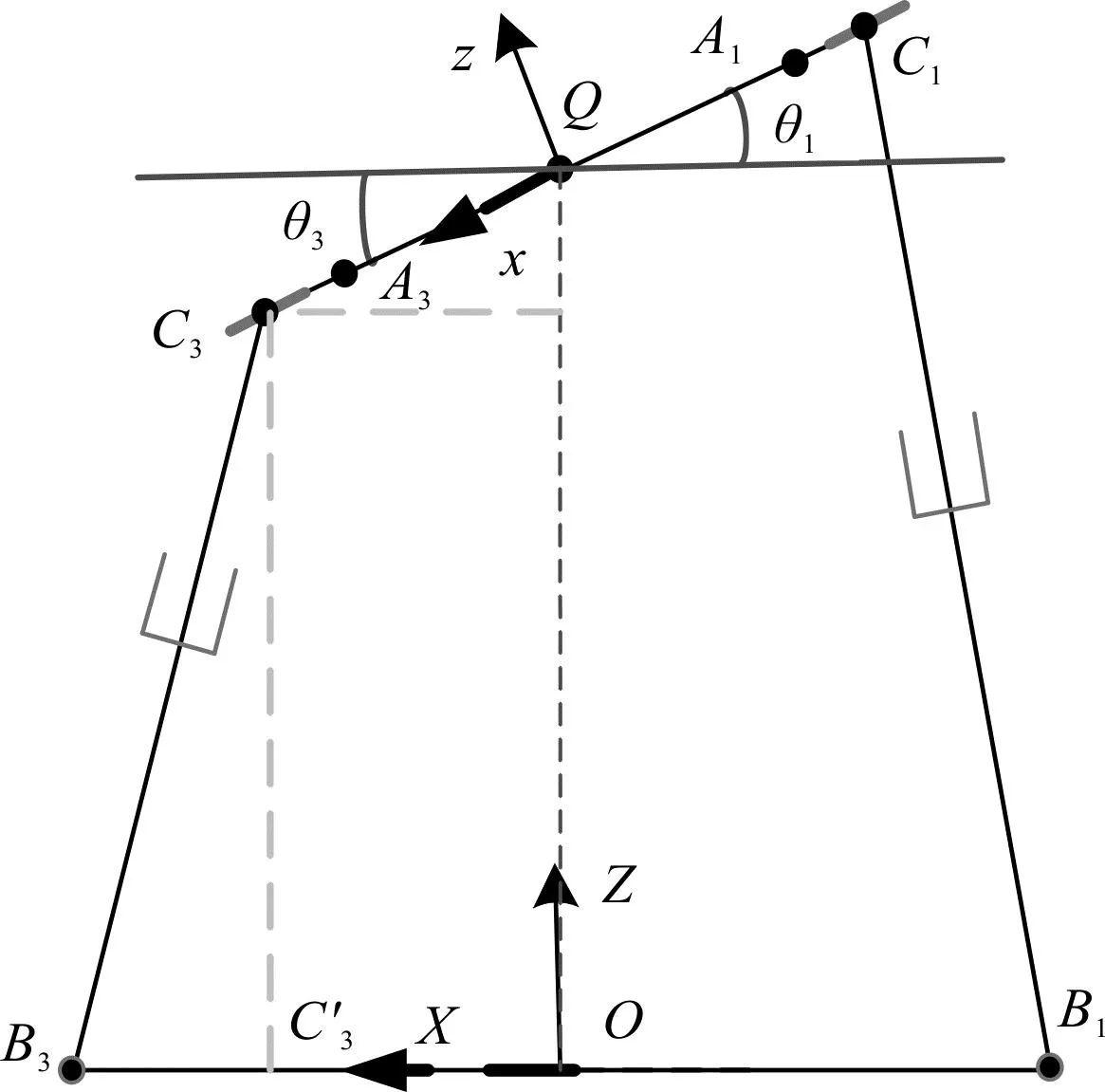
图2 θ3瞬时位形
若令θ1=θ3=θ,则:
(24)
根据分支伸缩杆的几何约束条件可得:
(25)
(26)
(27)
而由式(19)可计算出点C4(0,c,0)在定坐标系O-XYZ下的坐标,即:
(28)
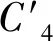
(29)
可计算得:
(30)

2.2 逆解验证
笔者给定结构尺寸参数c=60 mm、R=120 mm,根据式(25)~式(27)、式(30),利用MATLAB对机构逆解进行数值仿真,并绘制各分支主动关节的运动曲线,用虚线表示;同时,利用SOLIDWORKS进行虚拟样机建模和运动学逆解仿真,并用点画线表示。各软件的仿真曲线为4条,仿真时间t为20 s。
仿真结果如图3所示。
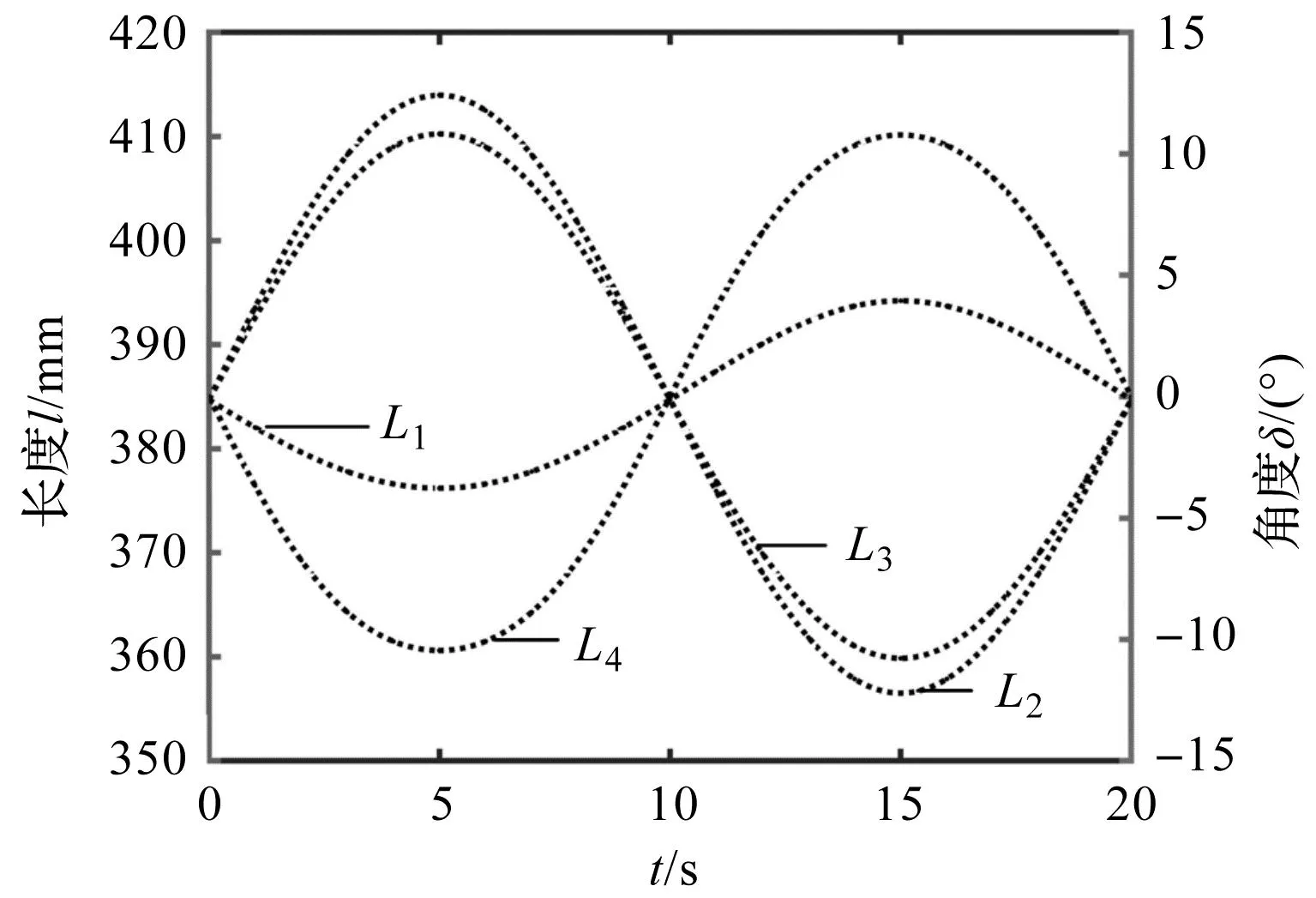
图3 逆解仿真曲线
图3中,对比两种不同软件做出的运动仿真曲线可知:每两条曲线重合,表明仿真结果一致,验证了机构逆解理论分析的正确性。
3 基于P-ABC算法的正解分析
3.1 机构运动学正解模型
由于直接建立机构运动学正解的解析方程比较困难,因此,笔者根据机构主动输入线位移li和角位移δ(用l4表示δ),求解同时满足逆解方程式(25)~式(27)和式(30)的α、β、γ和z的值,以达到运动学正解的数值求解目的。
机构的逆解方程可进一步改写为:
li-fi(α,β,γ,z)=0(i=1~4)
(31)
笔者将式(31)转化为带约束的多目标非线性方程最小化问题,建立机构正解的求解模型,即:
(32)
(33)
式中:fPS为算法的适应度,表示总体误差,其值越小,求解精度越高。
3.2 粒子-人工蜂群算法的构建
在实际应用中,并联机构快速准确的控制效果取决于运动学正解的求解精度和响应时间。笔者融合ABC与PSO算法,提出了一种基于P-ABC算法的并联机构运动学正解求解方法。
3.2.1 ABC算法
ABC算法来源于自然界蜜蜂寻找蜜源采蜜的过程,如图4所示。

图4 蜜蜂采蜜过程
算法模型包括蜜源、引领蜂、观察蜂和侦察蜂。引领蜂发现蜜源后返回蜂巢,在舞蹈区内与观察蜂交流蜜源信息,并以一定概率雇佣观察蜂探索当前蜜源或被雇佣去探索其他蜜源,概率由蜜源的质量决定。若当前蜜源被探索完毕,引领蜂将放弃当前蜜源并转化为侦察蜂,以侦察蜂巢附近的新蜜源。
3.2.2 PSO算法
PSO算法来源于对鸟群觅食行为的研究,并将鸟群中的个体简化为具有位置和速度的粒子。
鸟类觅食的过程如图5所示。

图5 鸟类觅食过程
鸟类觅食的方向受两个因素的影响,一是自己曾经发现最多食物的地方Pp,二是在交流中获得的其他个体发现最多食物的地方Pg,最终在两者之间选择一个新方向。
3.2.3 P-ABC算法
PSO算法迭代速度快,但缺乏速度的动态调节,容易陷入局部最优,导致收敛精度低和不易收敛,其结果受到算法参数的影响。ABC算法虽迭代速度较慢,但每次迭代过程中都会进行全局和局部的最优解搜索,寻找最优解的概率高。
为提高求解并联机构正解的速度和精度,笔者提出P-ABC算法,其可以有效克服PSO算法易陷入局部最优解、求解精度低、ABC算法求解时间长的缺陷。相比于同类研究[25],其参数设置更为简单,计算量也更小。
在该算法中,蜜源和Pp对应优化问题中的可能解,其数量分别与引领蜂和粒子的数量相同,且一一对应。P-ABC算法包含两个阶段,每个阶段都以获取fPS最小值为正解计算结果的选择依据。
首先,在PSO算法中,在有N个粒子的D维搜索空间内,第i个粒子的位置和速度更新公式分别为:
(34)
(35)
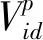

(36)
式中:xi,j为第i个蜜源的第j维值,i=1~N。
观察蜂在舞蹈区内获取全部引领蜂的蜜源信息,并采用轮盘赌的方式选择新蜜源,其选择概率为:
(37)
其中,fitMi为第i个蜜源的适应度,其表达式为:
(38)
引领蜂在舞蹈区进行蜜源信息交流后,获得新的蜜源为:
(39)
式中:φi,j为区间[-1,1]的随机数。
引领蜂变成侦察蜂后,根据下式获取新蜜源:
(40)

每只蜜蜂可通过贪婪法比较新旧蜜源的适应度fPS,并选择优势解作为新蜜源。算法完成设定迭代次数后,最小适应度fPS对应的蜜源为所求最优解。
3.3 算例分析
笔者分别利用ABC、PSO和P-ABC算法对3RPUPc-UPS并联机构的运动学正解进行数值求解,以验证P-ABC算法的优越性。
假定对三种算法设置相同的迭代次数,p值为总迭代次数的二分之一,其余算法参数选取常用数值。
为方便运算和比较三种算法的性能,笔者使用MATLAB中的GUI模块开发出基于三种算法的机构正解求解软件,其界面如图6所示。

图6 软件初始界面
以求解动平台位姿α=25°、β=34°、γ=23°、z=360 mm的正解为例,设机构的结构参数R=120 mm、c=60 mm;最大迭代次数取300,群体个数取100,ω=0.8,c1=c2=2;以及运动学逆解的计算结果,l1=332.048 mm、l2=390.904 mm、l3=402.294 mm和l4=-14.438 9°。
笔者将所有参数分别输入到软件界面相应的输入框内,点击正解计算,可得到三种算法的运行时间、求解误差、适应度值和适应度曲线,最后点击下载即可保存该位姿下的适应度曲线,如图7所示。
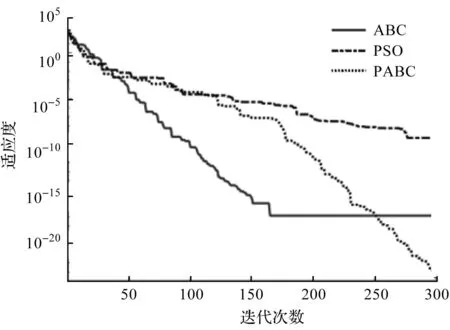
图7 适应度曲线
由图7可知:前150次迭代中,ABC算法收敛速度快于PSO和P-ABC算法的速度;150次迭代之后,ABC算法适应度曲线处于稳定状态,PSO算法处于缓慢收敛状态,而P-ABC算法加速收敛,并偏离PSO算法;在300次迭代终止时,P-ABC算法适应度值远小于ABC和PSO算法的值,该算法克服了ABC算法迭代中止和PSO算法求解精度低的缺陷。
软件独立运行30次后的误差均值如表1所示。

表1 算法独立运行30次的误差均值
从表1可知:相比于ABC算法,P-ABC算法运行时间缩短了50.02%,整体误差等级从10-18变为10-20;相比于PSO算法,其运行时间虽长,但误差等级从10-10降至10-20,降低了10个数量级。
为验证P-ABC算法的适用性,笔者选取50组不同位姿进行300次迭代正解求解运算,其中5组的计算结果如表2所示。

表2 P-ABC算法不同位姿下的运算结果
表2计算结果表明:P-ABC算法单次求解时间在0.5 s内,求解误差级别为10-20,能有效满足实际应用。
4 结束语
针对3RPUPc-UPS并联机构运动学正解求解困难的问题,笔者分析了3RPUPc-UPS并联机构的运动输出特性,并融合了PSO和ABC算法,提出了兼顾两者优点的P-ABC算法。
研究结论如下:
1)分析了机构的拓扑结构和方位特征集,计算得出其自由度为4,运动耦合度为2,表明机构具有较强的运动学耦合性;
2)利用机构几何特征建立了机构运动学逆解方程,推导出其解析表达式,并利用MATLAB和SOLIDWORKS软件仿真验证了逆解模型的正确性;
3)建立了机构运动学正解的数值求解模型,将运动学正解求解转化为含有约束的多目标非线性方程的最小化问题。算例分析结果表明,P-ABC算法不仅运算快、运行时间短,还具有求解精度高的优点。相对于ABC算法,P-ABC算法的运行时间缩短了50.02%;相对于POS算法,其求解精度提高了10个数量级。
在后续的研究工作中,笔者将对该算法参数进行优选,以获取最佳的工作性能,并将其应用于其他类型机构的运动学求解中,以验证该算法的通用性。

