金属盒盖自动扣合装置的优化设计及试验*
周 可,彭来湖,*,徐步都,李明华
(1.浙江理工大学 机械工程学院,浙江 杭州 310018;2.浙江理工大学 龙港研究院有限公司,浙江 温州 325802)
0 引 言
因具有良好的密封性、避光性,近年来,金属包装材料被广泛应用于食品、药品、化工等行业中,成为一种应用广泛的包装材料[1-4]。2022年全球金属包装市场规模达到了962亿美元,并将于2029年达到1 177亿美元的市场规模,增长势头强劲[5-6]。
要生产出具有良好密封性能的盒盖,需要多个步骤,如印刷、冲压、印花、合盖、理料[7]等。其中,对密封性影响最大的一个环节是对上盖和壳体进行合盖的步骤[8]。目前,合盖操作主要是以人工操作为主。这种生产方式具有很大弊端,主要表现在以下两个方面:1)生产企业对劳动力的需求增大,工人的工作强度较高,随着人工成本的不断增加,企业的生产利润日益降低;2)人工合盖速度较慢且合盖质量参差不齐,导致企业生产效率低、质检成本高。
针对合盖操作自动化程度低的问题,诸多学者都设计了合盖装置[9-14]。这些设计的合盖装置对旋合式金属、玻璃或者塑料包装材料有较大优势,提升了部分类型包装材料的自动化程度;但对于扣合式包装的合盖操作仍存在较大困难。为此,又有许多国内外学者对此进行了研究。
FORMENTINIG等人[15]针对金枪鱼压盖机提出了一种模块化的设计方法,满足了不同尺寸、形状罐头包装的生产需求;但其未介绍机器性能指标以及理论模型,无法为生产企业提供参考。岳翠萍等人[16]设计了一种机器人压盖机,并设计了相应的斜口挡盖导向板,提升了机构的压盖率;但其无法与上一工序相衔接,需要人工进行送料,整体生产系统不连贯。刘滨[17]针对啤酒压盖机设计了一种取盖、交接盖送料装置,降低了挤盖、损盖以及歪盖的发生率,将压盖合格率从93.5%提升至96.5%;但其并未对装置进行理论分析,仅通过试验的方式完成了结构设计。殷水忠[18]设计了一种饮料盒加盖去盖机构,使用气缸以及夹具固定蝶形阀盖,并对其结构参数进行了理论计算,其能够完成对蝶形阀盖的稳定压盖及去盖任务。BANKUTY[19]针对卡扣式盖子与容器,设计了一种抓取式封盖装置,采用容器两侧的气缸机械爪完成了精准定位工作,提高了合盖精度;但其需要人工进行补料、送料,整体生产效率低。
以上设计的扣合式合盖装置多以试验、调试的方式进行装置优化设计,缺少理论计算分析,无法为企业提供理论设计依据,并且未考虑与前置工序的衔接,需要人工进行送料,降低了装置效率,不能实现装置自动化作业。
针对以上问题,为提升装置整体的作业效率,笔者设计一种扣合式金属盒盖自动扣合装置,构建送料过程中的数学模型,分析装置工作效率的关键影响因素,以轨道倾斜角度、气缸推力和轨道宽度为试验因素,以物料下落时间变异系数和姿态水平度为优化目标,采用ADAMS仿真和响应面分析进行优化设计。
1 金属盒盖生产工艺
以制造方法进行划分,金属盒盖可以分为两类,即三片罐和两片罐。相较于三片罐,两片罐具有密封性好、生产效率高、节省原材料等优势,因此,两片罐[20]在现代金属包装盒盖生产企业得到了广泛应用。
此处以两片罐为例,其生产流程如图1所示。

图1 金属盒盖生产流程
由图1可见:生产流程可以分为4个环节,即印刷、剪裁、冲压和包装。其中,金属盒盖剪裁、冲压以及包装环节自动化程度较低。
为提升整体效率以及自动化水平,剪裁环节可以利用数控切割机进行剪裁;冲压环节可以利用伺服冲压机进行高速、高精度冲压。然而,目前市场上并没有成熟可靠的包装自动化设备以及相应的设计参考模板和理论依据。
金属盒盖扣合装置的设计关键点是:经过冲压工艺生产出的盒身与盒盖均以开口朝上的状态经过水平传送带快速进入下一工序,其现有姿态难以直接合盖,且进入合盖工序时的姿态情况复杂;因生产周期较短,盒身与盒盖进入装置时的速度以及冲量较大,对装置的冲击较大,易使装置产生无规律振动,导致合盖密封效果变差。
因此,必须通过理论模型计算、仿真分析以及试验手段对合盖装置进行结构参数优化,使扣合式合盖装置适应金属盒盖包装。
2 合盖装置总体设计
2.1 基本结构
扣合式合盖装置组成结构如图2所示。

图2 扣合式合盖装置组成结构
其中,送料模块是扣合式合盖装置的重要组成部分,其大致可以分为推送部件、送料部件以及卸料部件,其为合盖工序提供稳定的物料来源,且输送物料的稳定性与合盖能否成功高度相关。
现有滑道常常出现物料冲出滑道或停滞在滑道中,以及物料在滑落过程中旋转的现象,严重影响了扣合式合盖装置运行的稳定性。因此,需要着重对送料模块等关键性部件进行设计。
2.1.1 推送部件
推送部件的设计要求如下:
1)为了在推送过程中完成对物料姿态的矫正工作,L型箍的宽度应比物料稍宽,避免物料在推送的过程中旋转;
2)平推气缸应运动平稳,避免速度、加速度突变对送料的稳定性造成影响,以确保物料进给的高成功率。
物料的推送过程如图3所示。
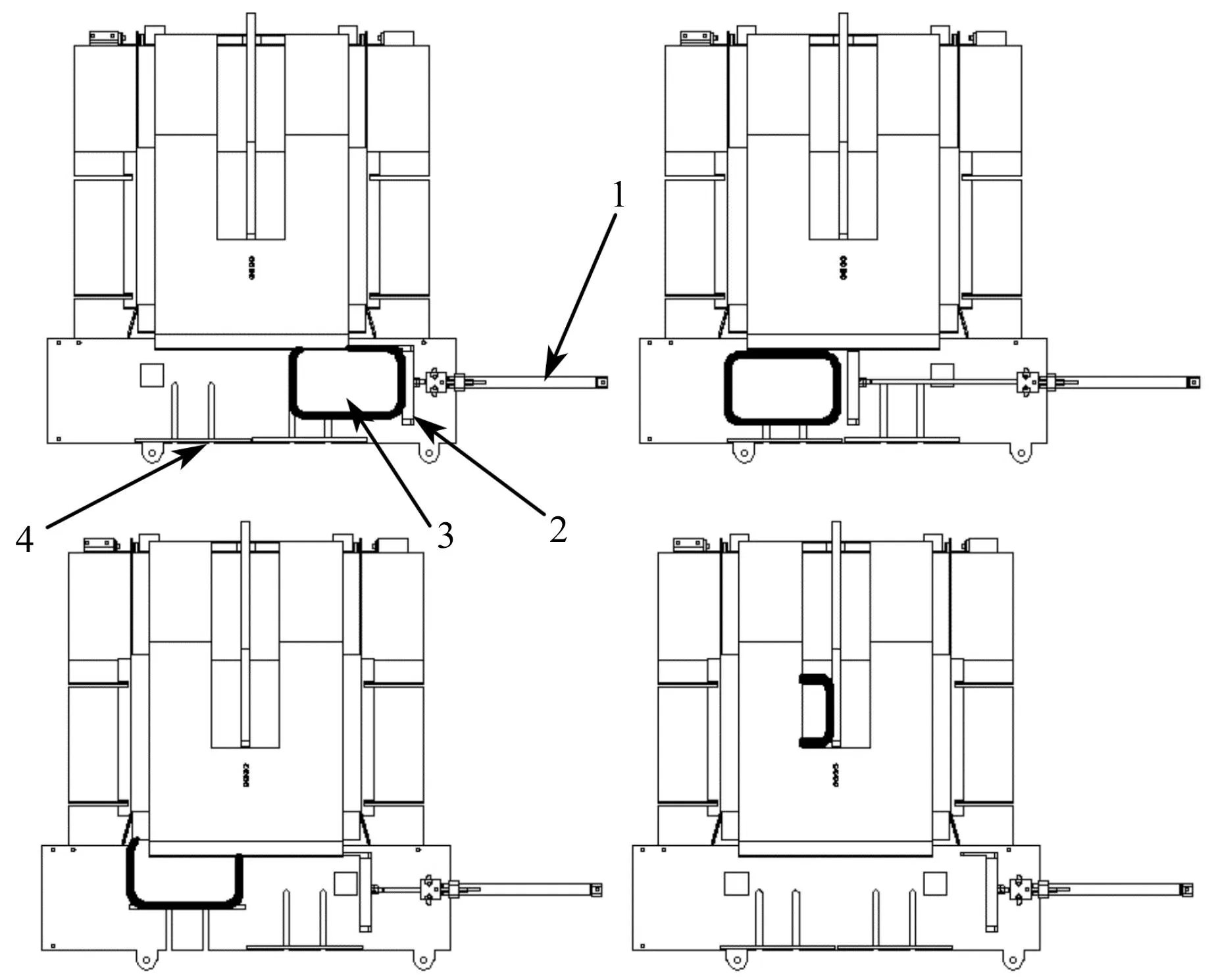
图3 推送物料过程
推送部件由平推气缸和L型箍以及活动气缸组成。在作业时,平推气缸驱动L型箍,将缓冲平台上的物料依次推至对应滑道入口,随后平推气缸缩回,对应滑道的活动气缸伸出,将物料推入排料滑道,推送完成后,平推气缸缩回。
2.1.2 送料部件
送料部件是送料模块中的核心部件。送料部件由直线滑道、圆弧滑道以及挡板组成。其中,中央挡板与侧面挡板将整个滑道分割为两个相同的送料轨道,相比于单个送料轨道,其可延长整体工作周期,避免送料速度过快、装置稳定性下降等问题。
送料部件主要参数包括:直线轨道倾斜角度与长度、圆弧轨道曲率与角度、轨道宽度等。
2.1.3 卸料部件
卸料部件主要由两个卸料气缸组成,以便送料滑道间歇性地卸出物料。
卸料部件工作原理如图4所示。
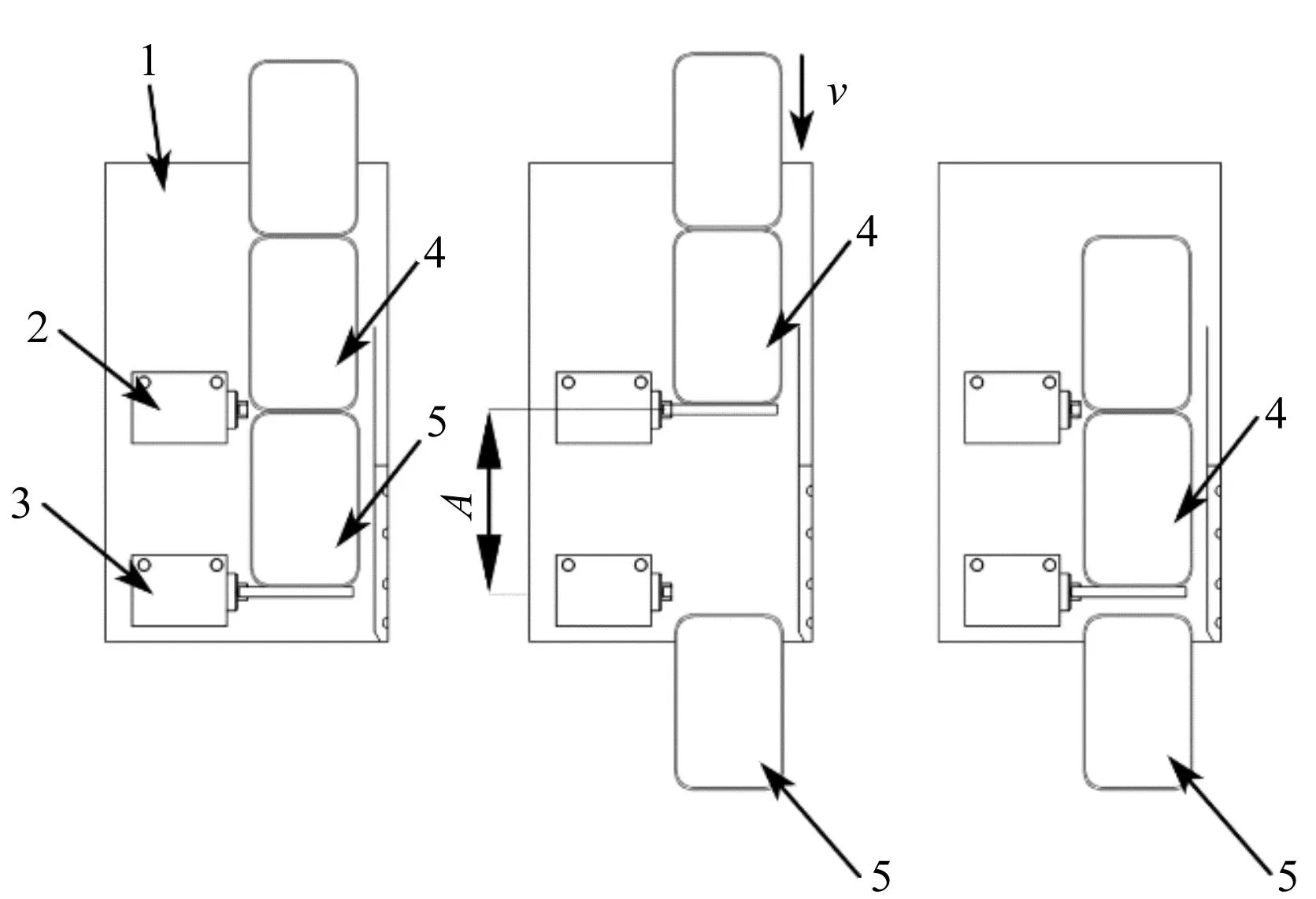
图4 卸料部件工作原理
卸料部件安装在圆弧滑道下方,卸料气缸一和卸料气缸二的活塞杆的初始状态分别为伸出和缩回,卸料气缸二将物料阻挡在排料滑道中,阻止物料进入下一工序,卸料气缸一的活塞杆伸出的同时卸料气缸二缩回,第一个物料从排料滑道滑入下方合盖凹槽;然后,卸料气缸一和卸料气缸二分别执行缩回和伸出动作,使得第二个物料进入第一个物料的初始位置,以完成单个物料的卸料。
两个卸料气缸中心点之间的距离A与物料长度相等,可以确保卸料气缸一挡住第一个物料,卸料气缸二活塞杆进入第一个物料与第二个物料之间的间隙,从而在每个卸料周期中完成单个物料的精确卸出工作。
2.2 整机结构与作业原理
装配后的扣合式合盖装置整体结构如图5所示。
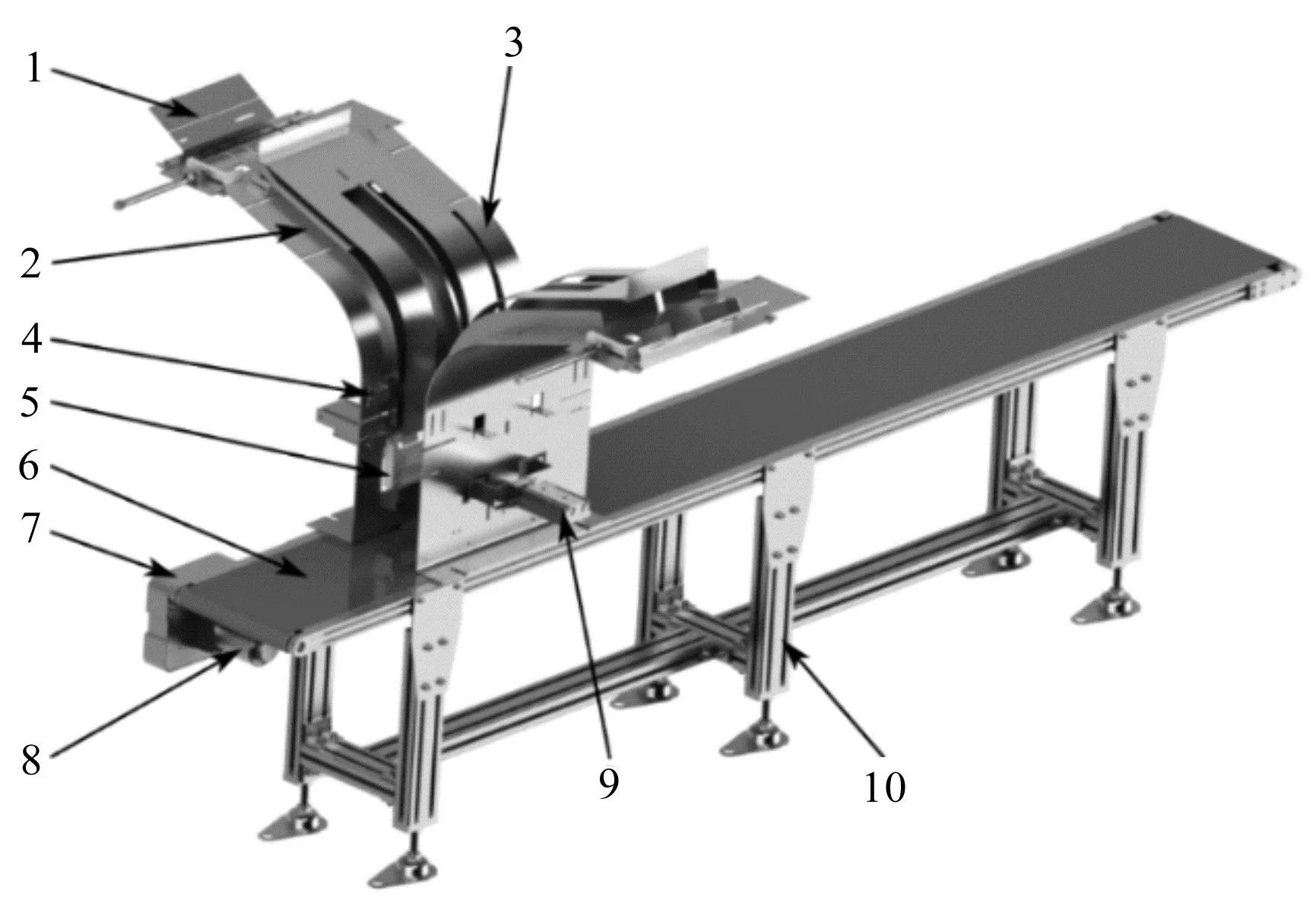
图5 扣合式合盖装置示意图
扣合式合盖装置作业时,盒盖与盒身分别从装置左右两侧的弹簧合页进入装置,并以一定初速度滑落至安装的接近开关处,接近开关通过接收物料进入平推位置的信号,控制平推气缸启动,平推气缸带动L型箍,将物料交替送至两个并排滑道入口处;随后,活动气缸伸出,将物料推入滑道,物料沿直线轨道、圆弧轨道滑落至处于伸出状态的卸料气缸处,等待前一工作周期的合盖工序完成。
前一周期的合盖工序完成后,卸料气缸缩回,盒盖与盒身分别继续下落至两侧放置槽处,等待两组盒盖与盒身进入放置槽后,合盖气缸伸出,带动合板将盒盖扣压入盒身,随后另一侧的传动气缸将合盖完成的整体从放置槽推入下方由电机驱动的传送带,进入下一工序。
由此可见,盒盖的送料速度、姿态、下滑的流畅程度以及整个工作周期时间是机构设计时需要考虑的核心因素。通过初步分析可知,其与盒盖送料速度、姿态与气缸推力、盒盖材料、装置材料、滑道倾角曲率以及滑道长度等因素相关。
因此,笔者重点考虑的影响装置性能的因素有:气缸推力、轨道倾斜角度、轨道曲率、轨道各段长度、轨道宽度、装置材料。
2.3 送料过程运动学及动力学分析
物料沿送料滑道滑落可以分为两个阶段:沿直线轨道滑落和沿曲线轨道滑落。在物料沿送料轨道滑落的过程中,物料需要依靠自身的重力以及活动气缸给予的推力运动,若直线轨道的倾斜角或曲线轨道的曲率太小,物料将停滞在滑道中;若直线轨道的倾斜角或曲线轨道的曲率太大,物料将冲出滑道。
由于滑道存在间隙以及活动气缸推力不均匀等因素,物料在滑落过程中难免倾斜旋转,并且由于旋转所产生的反作用力以及力臂,使得物料有加剧倾斜旋转的趋势。因此,需要结合物料滑落过程中的受力情况以及物料尺寸,对滑道宽度进行约束。
综上所述,需要对物料滑落运动过程的运动学和动力学进行综合分析。
物料包括壳体和上盖,其尺寸如图6所示。

图6 物料尺寸示意图
首先,分析直线轨道滑落阶段。
物料沿直线轨道滑动过程受力情况如图7所示。
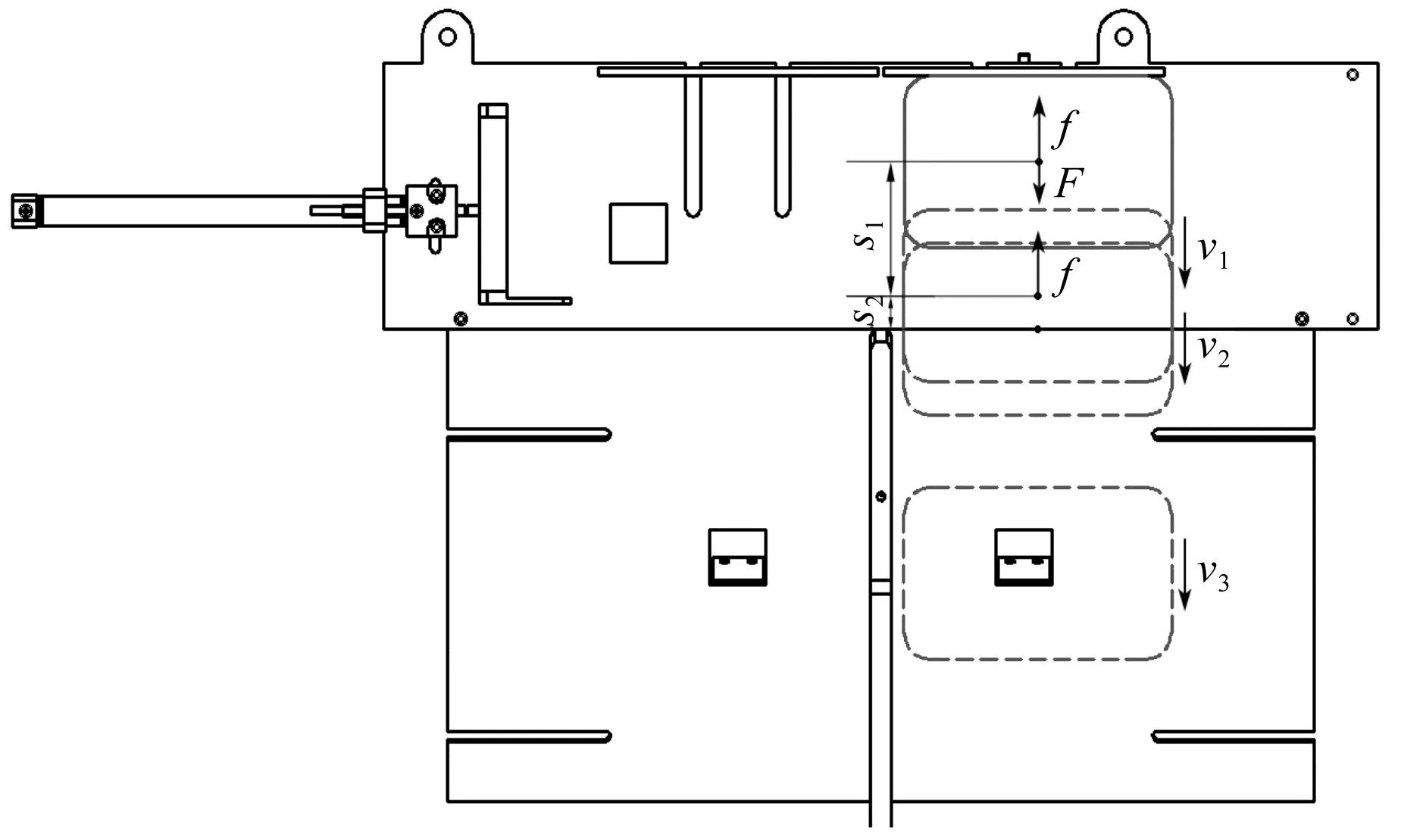
图7 直线轨道送料过程受力及运动分析

物料与轨道接触瞬间如图8所示。
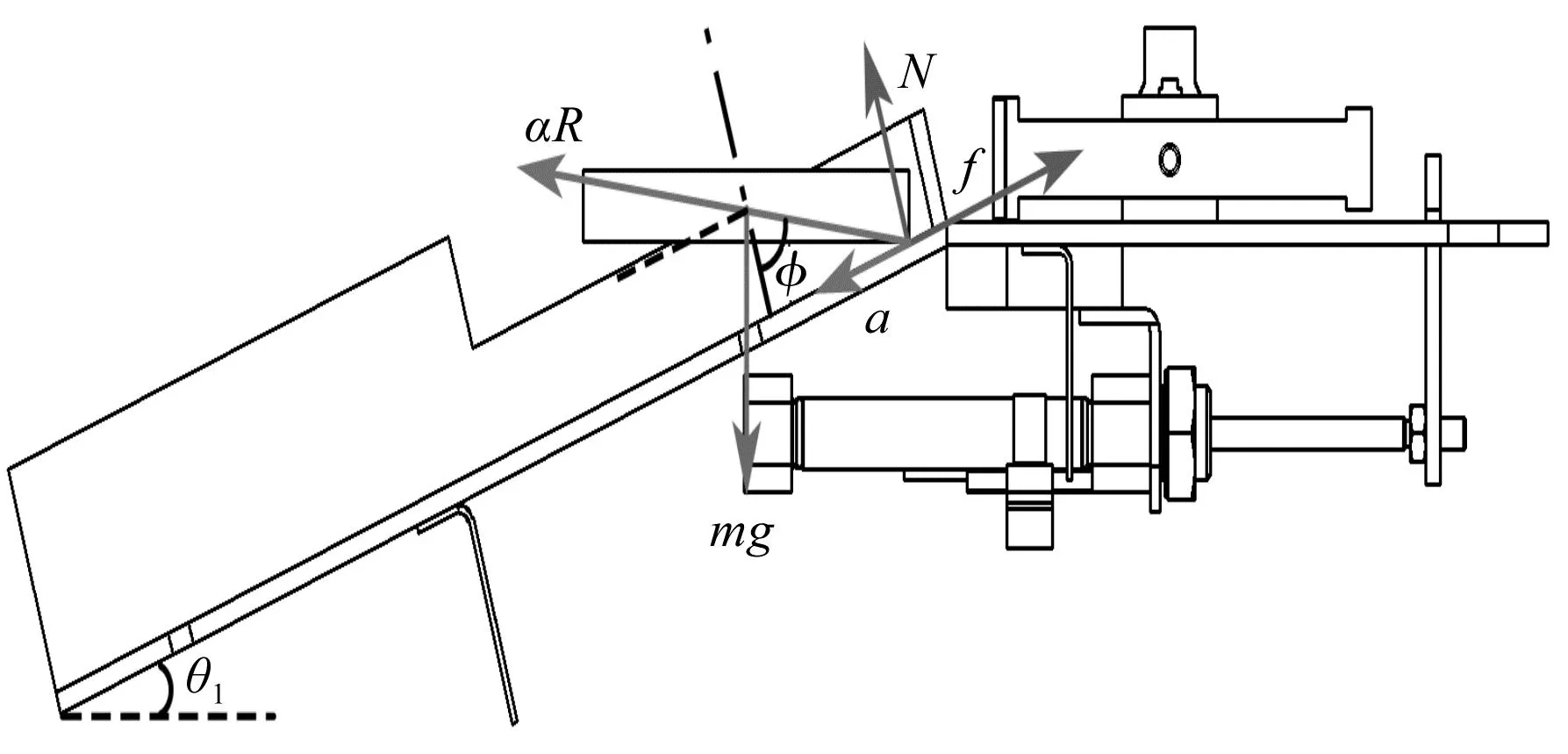
图8 物料与轨道接触瞬间受力及运动分析
由于角加速度的作用,物料的姿态将迅速地由水平于地面变为平行于斜面。为了简化模型,笔者将物料与轨道视为刚体,且在物料姿态改变过程中无弹性形变产生。因此,可以得到物料棱角与倾斜轨道接触瞬间的动力学方程为:
(1)
式中:acx与acy为质心加速度在斜面方向与垂直斜面方向上的分量,分别为acx=a+Rαcos(φ)与acy=Rαsin(φ);k为转动惯量系数,由物料质量分布决定。
由式(1)可得加速度与角加速度为:
(2)
(3)
当物料姿态完全平行于斜面时,物料在倾斜轨道上的滑行时间以及滑行结束时速度分别为:
(4)
(5)
由式(4)和式(5)可知,为了减小物料速度,应适当增加直线轨道长度或在轨道中增加防滑材料。
根据工作场地的实际情况,笔者确定直线轨道距离L为190 mm。在设计轨道倾角时,应在满足滑行时间小于最长分配时间0.11 s以及流畅滑落的前提条件下,尽可能地减小倾角角度。
由前述的机构设计尺寸计算可得v2≈1.72 m/s,L=0.19 m,笔者取g=9.8 m/s2,μ=0.24,并设置约束条件ts3=0.11 s,v3=2 m/s;将上述条件代入式(4)和式(5),可得θ1min≈14.5 °,θ1max≈29 °。
由于在实际运动中,物料与轨道的作用点并不一直位于物料质心,而是不断地沿着物料与轨道的接触面前后移动,从而使得一个额外的惯性力作用于物料。因此,需要将轨道倾角的最大值缩小为理论计算结果的0.8倍,以降低物料倾倒的可能性。
人才的培养归根结底还是要反哺社会,这也是实现个人社会价值的基本体现。让社会企业以及行业协会等多方参与到校企合作人才培养方案的制定,从源头规划发展,量体裁衣,能够更好地促进人才成长,使学校的专业设置以及课程体系与企业的发展相接轨,同时,有效地减少学校教学资源成本,精准施教。社会企业和行业协会的积极参与,还可以充实学校的教学资源,及时带来行业、社会热点动态,活跃教学内容,达到产教结合,学以致用的良好局面。以理论指导实践,在实践中检验理论的教学结合模式,从实践中来,到实践中去,能够更好地促进人才培养,快速地转化成生产结果,达到多方共赢的良好局面。
综上所述,笔者将直线轨道倾斜角度取值范围设为14.5 °≤θ1≤23.5 °。
其次,需要分析圆弧轨道滑落阶段,物料沿着存在摩擦的圆弧轨道滑落。
圆弧轨道物料受力情况如图9所示。

图9 圆弧轨道送料过程受力及运动分析
物料下滑过程的动力学方程为:
(6)
将式(6)沿切线以及法线方向进行分解,可得到其分量,再将其与f(γ)=μN(γ),v(γ)dt=Rdr联立,可得到:
(7)
(8)
由图9可知,α=γ+θ-Γ,即dsinα/dγ=cosα,dcosα/dγ=-sinα,且将式(7)与式(8)联立,可得:

(9)
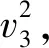

(10)
式(10)即为物料下滑所对应转角与速度关系。
轨道角度及曲率半径与物料速度的关系如图10所示。
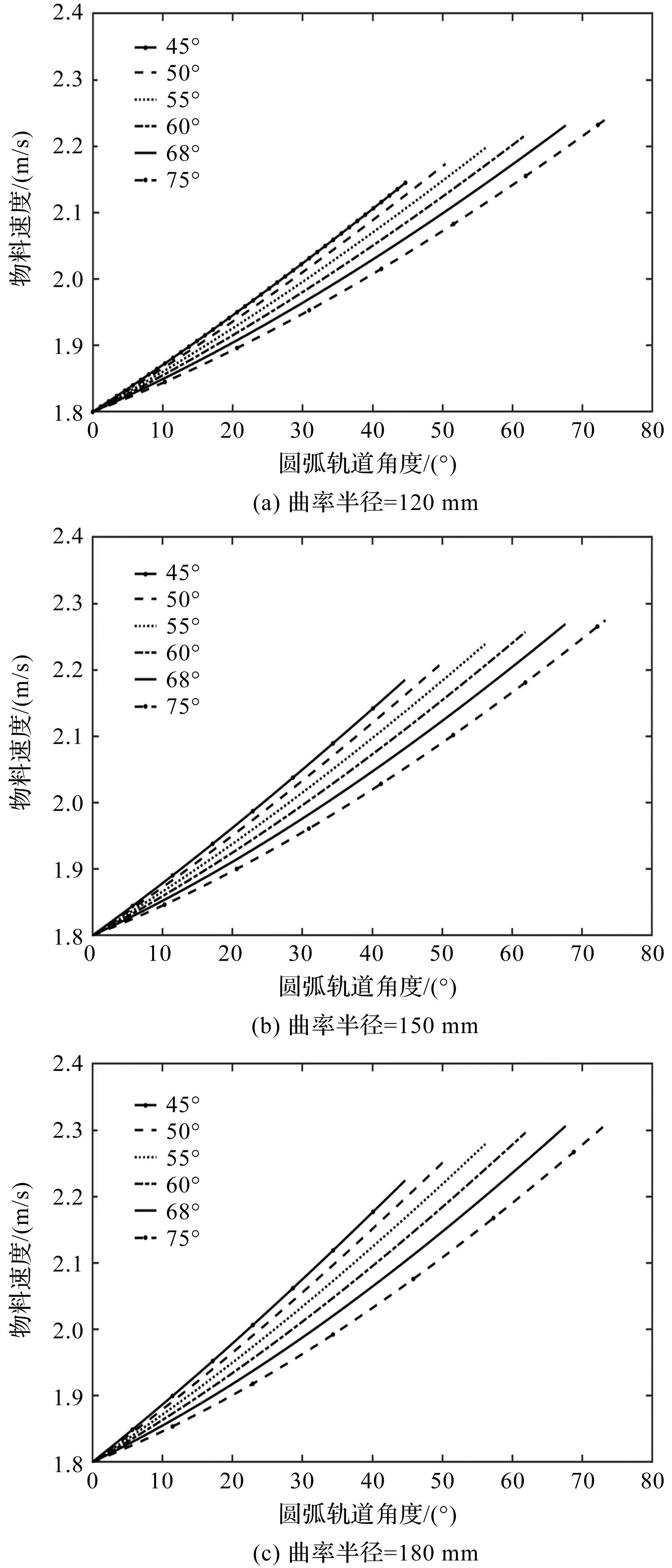
图10 圆弧轨道角度及曲率半径与物料速度的关系
当物料速度过低,送料时间超过装置整体工作周期时,容易发生物料的堆叠、卡顿;若物料速度过快,则容易刮伤物料表面。因此,笔者选取物料速度整体范围适中的150 mm曲率半径作为装置的曲率半径。
由图10可知:物料最终速度相近,但随着圆弧轨道角度的增加,物料速度的增量减小,速度变化更为平稳,所以在取值范围内应该尽可能地选取较大角度。笔者确定75 °为装置圆弧轨道角度。
由于在求解物料下滑速度过程中,支持力函数N(γ)与摩擦力函数f(γ)被联立消去,无法得到具体函数表达式,所以笔者对物料下滑过程做进一步分析。
首先,将物料受力沿切线方向和法线方向进行分解,则有:
(11)
(12)
式中:μ为物料与轨道接触表面之间的滑道摩擦系数;β=2Γ-γ。
将式(12)对时间求导,并将其与v=Rdβ/dt联立,可得:

(13)
假设物体在下滑过程中不飞离圆弧轨道,考虑边界条件,当物体位于轨道末端时,其所受轨道支持力为0,故将边界条件N(0)=0代入式(13),求其解可得:
(14)
至此,物料在圆弧段下滑的理论模型建立完成,圆弧轨道设计完成。
最后,笔者结合物料尺寸及其在滑落过程中的受力情况,对滑道宽度进行设计。
物料在滑道中的受力情况如图11所示。

图11 物料滑落旋转受力分析
从11图中不难看出:B=L+e,间隙e的取值应该以物料能顺利通过滑道,而保持水平姿态为准。并且物料在滑道中旋转而产生的反作用力N与其力臂αf组成的力矩会使物料存在绕O点继续旋转的趋势。当物料对角线长度C等于或小于滑道宽度B时,物料存在卡顿或姿态不稳的风险。因此,必须保证物料对角线与水平线的夹角θo大于摩擦角ρ。
根据图11中几何关系可得:
(15)
(16)
式中:f为物料与滑道侧壁的滑动摩擦系数。
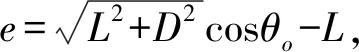
(17)
式中:h为物料的长宽比L/D。
由式(17)可知,最大间距emax与物料长宽比h以及滑动摩擦系数f有关。而在实际生产中,由于壳体与上盖都经过了圆角处理,模型更加容易发生旋转。因此,在计算最大间距emax时,需要将物料与滑道的滑动摩擦系数f扩大为实际的1.2倍,以减小最大间距emax。
笔者将实际物料尺寸代入式(17)中,可分别得到上盖轨道emax=13.668 mm,壳体轨道emax=12.657 mm。因此,上盖与壳体轨道的最大宽度Bmax分别为118.66 mm与114.35 mm。
综上所述,笔者确定二者的轨道宽度范围为105 mm~118.66 mm与101.7 mm~114.35 mm。
3 送料过程仿真与分析
3.1 滑道及物料模型的建立
笔者在SolidWorks中建立送料滑道模型,并添加一定约束,利用SolidWorks与ADAMS的接口程序,将滑道模型保存为“.x_t”格式,并将该模型导入ADAMS中。
仿真整体结构设置如图12所示。
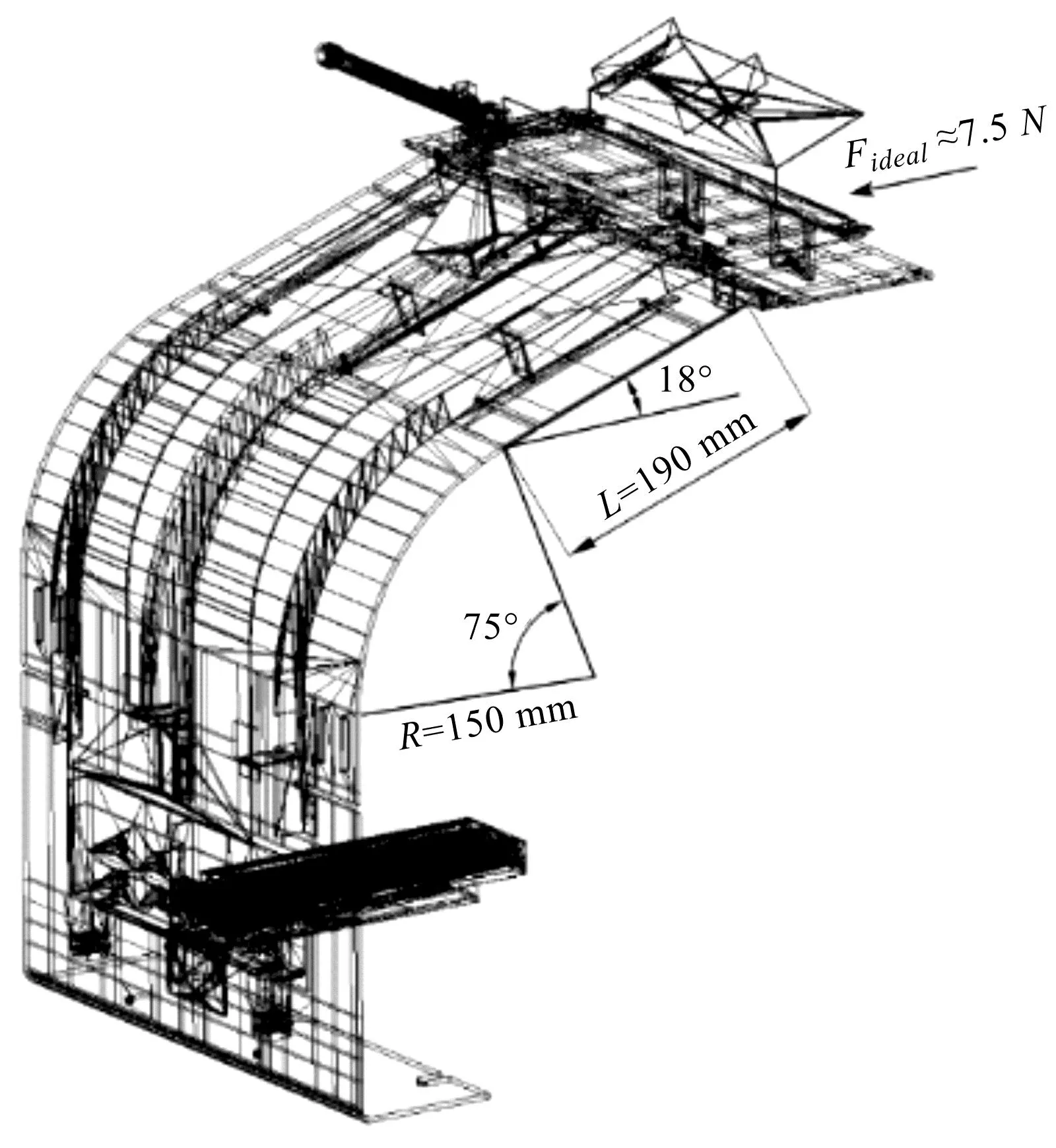
图12 ADAMS仿真整体结构设置
笔者在ADAMS中建立两种物料模型,分别为壳体与上盖,其结构与尺寸与图6所示一致。
在实际生产中,物料所使用材料为马口铁,但ADAMS中没有马口铁的材料选项。因此,笔者在ADAMS中新建一种材料,命名为“Tinplate”,参考马口铁特性,设置其弹性模量为2.1 GPa,密度为7 850 kg/m3[21],泊松比为0.27;此外,滑道材料为SUS304不锈钢,因此设置其弹性模量为194 GPa,密度为7 930 kg/m3,泊松比为0.3。
3.2 基于ADAMS和Simulink的送料过程仿真
笔者将滑道与物料模型整合入ADAMS后,设置其重力加速度以及相应的移动副、固定副约束,同时参照各类材料的接触参数,设置接触参数数值。
材料接触参数设置如表1所示。

表1 材料接触参数
在运行仿真之前,笔者需要设置速度、加速度、接触力测量函数以及变量单元,用于测量物料下落期间的运动学参数。同时,为了确保仿真的精确性,在滑道出口处设置一个传感器,当物料运动到卸料气缸处时,停止仿真,由此得到物料滑落时间。
以上设置完成后,笔者将活动气缸设置为代数变量单元,并将其作为整体机械系统的输入端,使用ADAMS将整体机械系统导出为.m文件,并使用MATLAB中的Simulink模块打开此文件,建立电磁换向阀以及气缸的数学模型方块图。
完成后的整体联合仿真模型如图13所示。
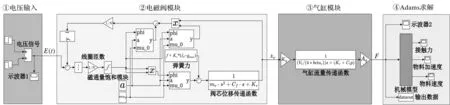
图13 联合仿真模型方块图
整体仿真信号变化过程为:电信号-位移信号-力信号。其中,电压信号是人为给定的方波信号模拟真实情况下的电磁阀得电过程。
笔者根据仿真结果得到了阀体的线圈电压及气缸输出力的动态仿真曲线,如图14所示。

图14 线圈电压及气缸输出力的动态仿真曲线
由图14可知:方波信号高电平持续时间为0.043 s,且由气缸输出力曲线可知,电磁阀由开启到完全关断状态耗时约为0.065 s。
笔者再将气缸输出力与封装的机械模型输入端相接,并调用ADAMS机械模型子函数对测量参数进行求解,同时观察ADAMS仿真动画,运行仿真,得到各个测量参数随时间的变化曲线。
物料速度、加速度曲线和物料与各个约束结构的接触力曲线如图15所示。
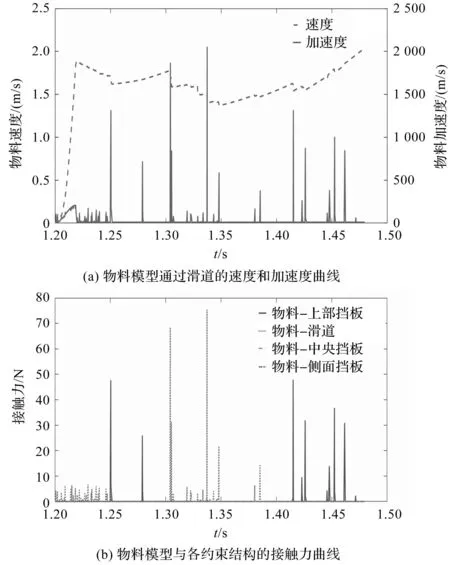
图15 ADAMS与Simulink联合仿真结果
从图15中可以看出:在整个运动过程中,物料与侧面挡板的接触力为0 N,仅在1.32 s时与中央挡板有微小的接触力,即物料仅与约束物料水平姿态的中央挡板有轻微碰撞。由此说明滑道宽度设计合理。
但在1.3 s和1.33 s时,物料与滑道发生碰撞,并产生了较大接触力,易导致物料发生形变或造成物料表面损伤。因此,在实际装配滑道时,应考虑在对应位置处增加额外的缓冲结构或缓冲措施,以减小物料瞬间冲量。
同时,在1.41 s时物料前端与上部约束挡板发生碰撞,且后端于0.04 s后在相同位置发生碰撞,这表明该处的上部挡板约束效果不佳,应减小上部挡板在该处的曲率半径。
结合图15(a)以及图15(b)可知,物料加速度曲线与物料接触力曲线高度吻合,由此表明造成物料加速度突变的主要影响因素为上部挡板、滑道的空间约束位置以及结构。
若要减小物料加速度突变,提高送料的稳定性,应考虑对上部挡板、滑道的空间位置以及约束点做出调整。
在假设的初始条件下,物料在滑道中通过的整个仿真过程,滑道“特殊处”是否有缓冲结构、上部约束挡板能否使物料贴合滑道运动是送料过程是否稳定的关键。且物料在结束圆弧滑道时的速度为2.026 m/s与理论计算值2.254 m/s之间的误差为10.1%。其原因主要是由于在理论分析时,笔者将物料以及滑道均视为刚体,忽略了运动过程中的弹性形变与其产生的弹性力对加速度、速度的影响。
4 试验设计和结果分析
4.1 试验方法
目前,常用的试验设计方法有线性回归分析法、正交设计法、拉丁方设计法和响应面分析法等。数理统计方法(如线性回归分析)仅能评估单因素影响,但笔者研究3个因素的相互影响,因此不宜选择该方法。正交试验设计法无法给出最优指标,不能实现因素全区域上的参数优化目的,因此同样不宜选择该方法。
响应面分析方法中的Box-Behnken设计具有试验次数较少、可同时评估多因素影响、响应量回归方程精度高等特点。因此,笔者选择Box-Behnken为该实验的方法。
Box-Behnken整体流程如图16所示。

图16 Box-Behnken设计流程
4.2 试验条件和指标
为确定最优结构和参数组合,笔者于2023年1月在浙江理工大学龙港研究院智能制造实验室进行了试验。试验所用样机如图17所示。

图17 扣合式合盖装置样机
图17中,送料气缸为亚德客有限公司生产的迷你气缸,型号为MI8X35SCA,缸径8 mm,工作气压0.15 MPa~1 MPa。试验物料选用温州捷辉包装有限公司生产的马口铁包装盒。
试验中,轨道倾斜角度范围为14.5 °~23.5 °,轨道宽度分别为105 mm~118 mm,102 mm~114 mm,试验气缸的推力范围为7.6 N~10.6 N。
笔者采用响应面优化法,并以轨道的倾斜角度、宽度和气缸的推力作为影响因素,以物料下落时间变异系数、物料姿态水平度作为优化目标,对送料滑道的参数进行优化。其中,物料下落时间变异系数是指物料滑落的连续性与均匀性,物料下落时间变异系数越小,表明物料滑落得越均匀、越连续、效果越好。
计算物料下落时间变异系数[22]按下式计算:
(18)

姿态水平度是指物料滑落过程中与地面的平行度,姿态水平度越大,表明物料姿态越水平,效果越好。姿态水平度计算如下:
(19)
式中:y2为姿态水平度;θc为物料与地面的夹角。
轨道倾斜角度、气缸推力和轨道宽度编码如表2所示。

表2 Box-Behnken试验因素水平及编码
4.3 试验方案和结果
笔者使用Design-Expert 12软件进行试验的设计分析、数据处理以及统计归纳[23],并根据Box-Behnken试验结构进行优化设计。试验方案及结果如表3所示。
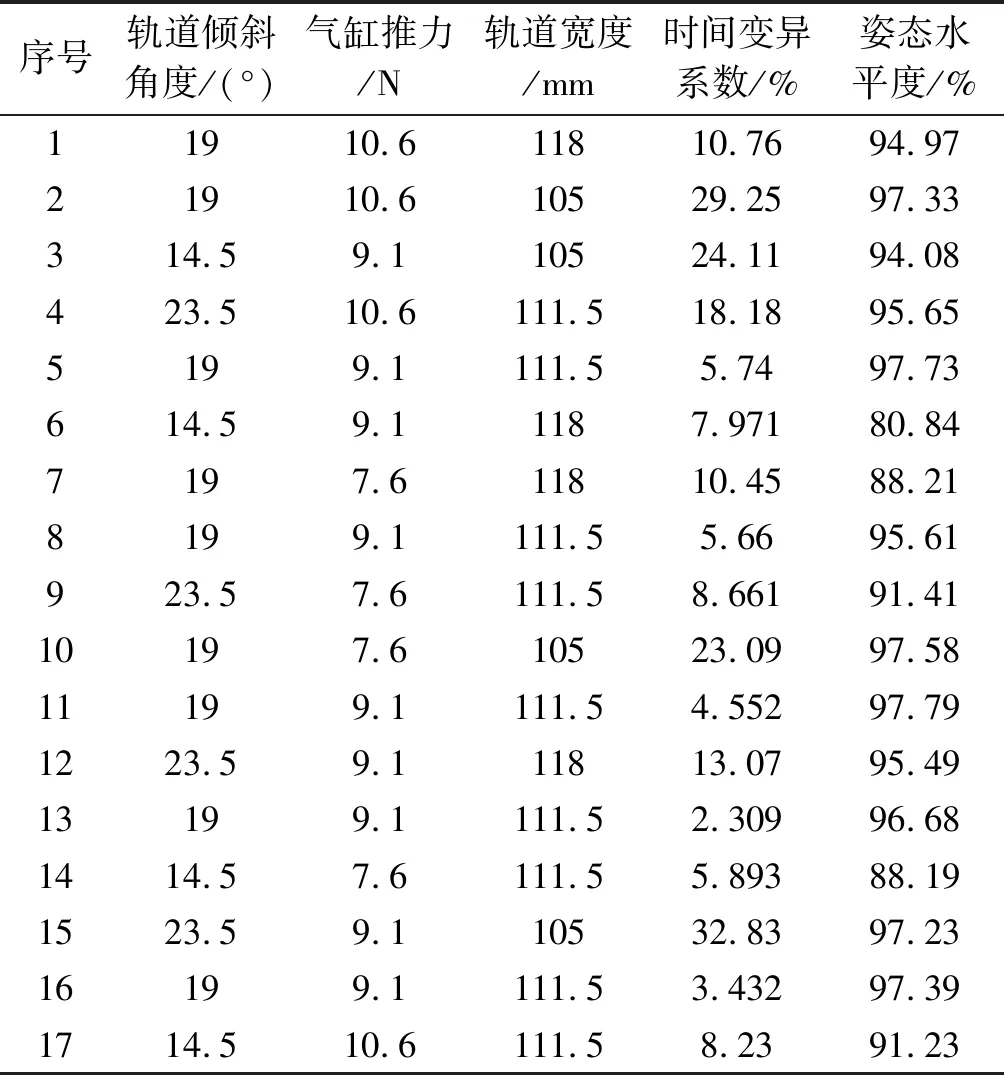
表3 试验设计方案及结果
根据表3的数据,两个指标的回归模型方差分析如表4所示。
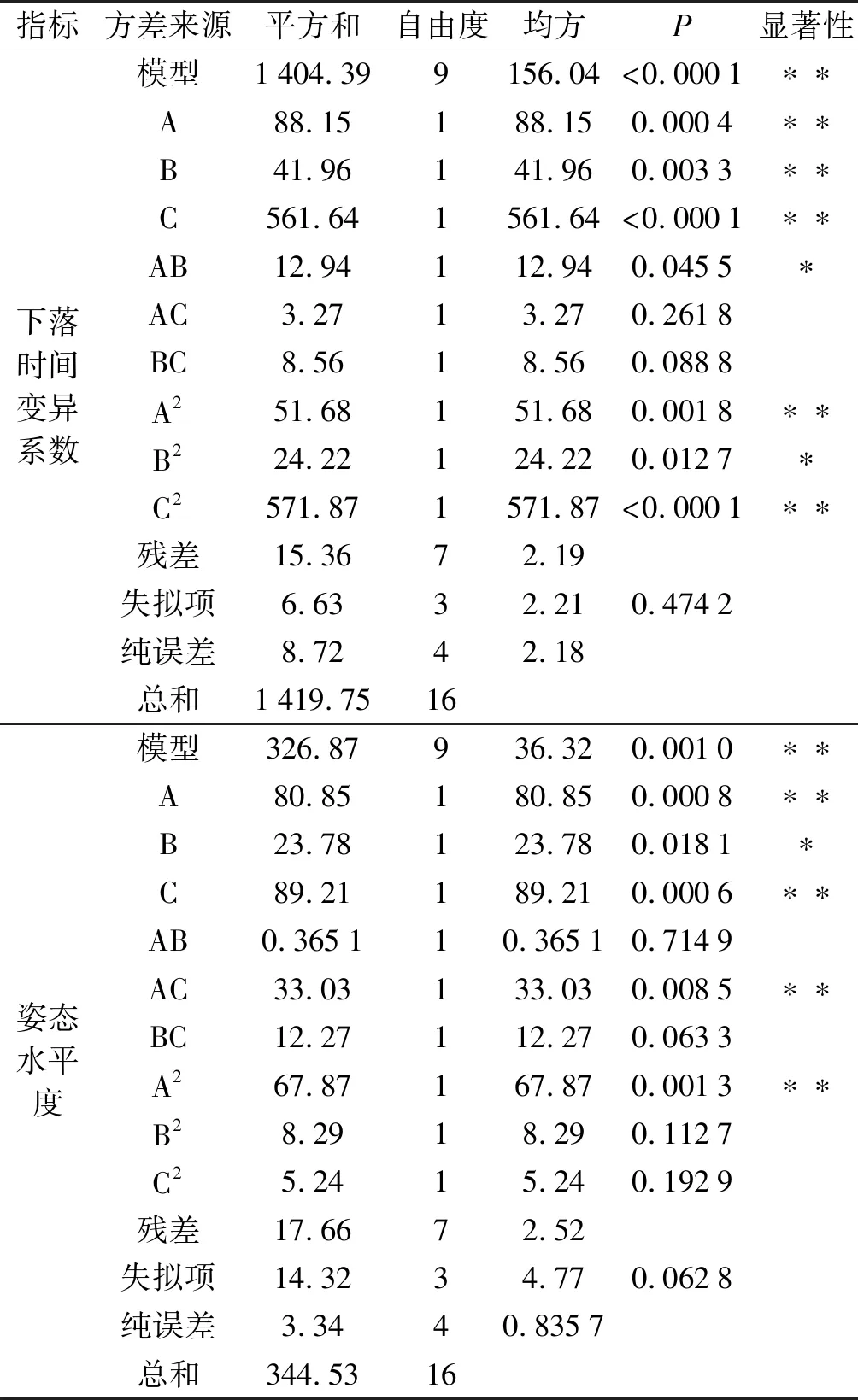
表4 回归模型方差分析
根据表4可知:两回归模型的P均小于0.01,表明模型高度显著;两模型失拟项的P均大于0.05,表明回归模型拟合程度高。
由轨道倾斜角度、气缸推力、轨道宽度的P可判断3个试验因素对下落时间变异系数与姿态水平度的影响程度,试验因素对下落时间变异系数的影响大小依次为轨道宽度>气缸推力>轨道倾斜角度;对姿态水平度的影响大小为轨道宽度>轨道倾斜角度>气缸推力;两模型的决定系数R2分别为0.989 2、0.948 7,均大于0.93,这表明模型可以解释93%以上的响应值变化,且预测值与实际值之间误差较小;两模型变异系数分别为11.75%、1.69%,表明模型具有较高可靠性。
综上可知,可用该模型对响应值进行分析和预测。
剔除不显著的影响因素后,笔者根据表4得到物料下落时间变异系数y1、姿态水平度y2的多元回归方程:
y1=4.34+3.32A+2.29B-8.38C+1.80AB+
3.50A2+2.40B2+11.65C2
(20)
y2=97.04+3.18A+1.72B-3.34C+
2.87AC-4.01A2
(21)
各因素交互作用的3D响应曲面如图18所示。
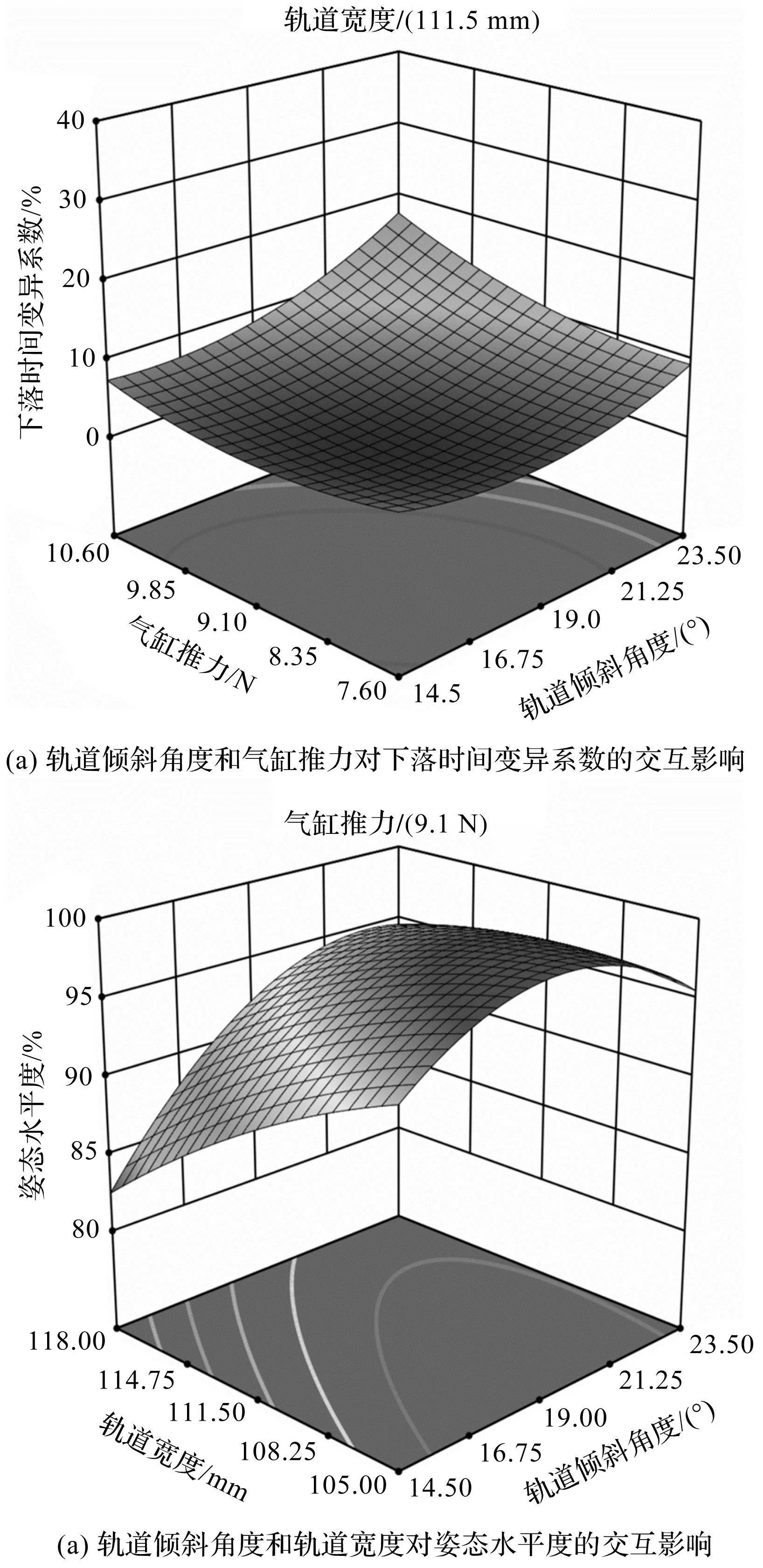
图18 因素交互作用对响应值的影响
图18(a)为轨道宽度位于中心水平(C=111.5 mm)时,轨道倾斜角度A与气缸推力B对下落时间变异系数y1交互作用的响应面曲面图。
当轨道倾斜角度A较大(A>19°)时,随着气缸推力的增大,下落时间变异系数迅速增大;当轨道倾斜角度A较小(A<19°)时,随着气缸推力的增大,下落时间变异系数先减小后缓慢增大,其原因是气缸推力越大,物料进入轨道时的初速度也越大,使得物料与位置约束零件发生干涉的可能性增大,从而使得物料下落不稳定、不连续。
当气缸推力一定时,下落时间变异系数随着轨道倾斜角度的增大而增大,且增大的幅度与气缸推力呈正相关,其原因是随着轨道倾斜角度的增大,物料运动过程中的加速度也随之增大,使得物料可能飞离圆弧轨道发生干涉,影响下落时间。
图18(b)为气缸推力为9.1 N时,轨道倾斜角度A与轨道宽度C对姿态水平度y2交互作用的响应面曲面图。
当轨道倾斜角度一定时,姿态水平度随着轨道宽度的增大而减小,且当轨道倾斜角度较小(A<19°)时,减小幅度较大,其原因是轨道宽度越大,则物料在下落过程中产生的旋转力矩以及概率也越大,而旋转力矩会增大物料的旋转角度,从而使得姿态水平降低;当轨道宽度一定时,姿态水平度随着轨道倾斜角度的增大而先增大后减小,其原因是当轨道倾斜角度过小时,物料在轨道中运动的加速度较小,使得物料与轨道力的作用点改变得更为频繁,从而使得发生旋转的概率增大,而轨道倾斜角度过大时,物料则更易与位置约束零件发生干涉,从而影响物料的姿态。
4.4 参数优化和对比试验
为获得扣合式合盖装置作业的最优参数,确定目标优化函数的约束条件如下式所示:
(22)
根据约束条件以及多元回归方程,笔者运用Design-Expert 12软件中的优化功能,对下落时间变异系数以及姿态水平度进行优化求解,得到最优工作参数:轨道倾斜角度为19.63°、气缸推力为9.28 N、轨道宽度为112.44 mm。此时下落时间变异系数为4.21%、姿态水平度为97.19%。
为了验证Box-Behnken试验的准确性以及参数优化的有效性,笔者选择最优参数组合进行5组试验验证,每组进行20次连续的完整作业流程,每个物料送料完成后,记录其平均下落时间变异系数以及姿态水平度,并记录整体合盖效果。
笔者按照上述试验方法进行试验,在试验过程中使用摄像机Canon80D对各个工序的作业情况进行记录。
各工序作业情况如图19所示。

图19 各工序作业情况
图19中,所示工序整体耗时0.9 s,小于盒盖生产周期,且物料在装置运行过程中无卡顿,基本满足作业要求。
五组下落时间变异系数和姿态水平度结果如表5所示。

表5 最优参数组合下的测试结果
由5表可知:下落时间变异系数与姿态水平度的相对误差均小于5%,证明了参数优化的有效性。
在100次完整作业流程中,成功合盖99次,成功率达到99%。
整体合盖作业效果如图20所示。

图20 扣合式合盖装置合盖作业效果
其中成功的合盖效果如图20(a)所示,壳体与上盖扣合紧密,上盖无歪斜和脱落情况,盒盖整体无形变,表面无刮伤。
失败的合盖效果如图20(b)所示,壳体仅有一端与上盖扣合,上盖歪斜,且易脱落,其失败原因为上盖在送料过程中因轨道物料较多而滞留于倾斜轨道中,在与下一生产周期物料接触时产生了较大冲量,导致在合盖工序中姿态歪斜,从而使壳盖下方先于上方扣合,且对上方扣合产生阻碍作用,最终导致扣合失败。
5 结束语
针对当前扣合式金属盒盖包装过程中自动化程度低以及成品质量参差不齐等问题,笔者提出了一种金属盒盖自动扣合式合盖装置。
笔者首先对装置的送料过程进行了运动学及动力学建模;其次,对送料过程进行了ADAMS与Simulink联合仿真,以验证模型的正确性;进一步应用Box-Behnken设计优化了装置工作参数;最后,通过对比试验分析,验证了该参数优化的有效性和可靠性。
主要结论如下:
1)该扣合式合盖装置主要由送料部分、合盖部分以及传动部分组成。笔者建立了送料过程的数学模型,根据理论计算结果,确定了轨道曲率、角度、长度的取值,以及轨道倾斜角度、宽度、气缸推力的取值范围;
2)运用ADAMS运动仿真软件以及Simulink模块对物料在滑道上的运动学、动力学特性进行了仿真分析,结果表明,上部挡板以及滑道的空间约束位置是造成物料加速度突变的主要因素;
3)进行了三因素三水平中心组合设计的Box-Behnken试验,优化后的倾斜角度、气缸推力、轨道宽度分别为19.63°、9.28 N、112.44 mm,此时物料下落时间变异系数为4.21%,姿态水平度为97.19%,表明优化后的送料过程更加流畅、平稳;
4)对优化后的装置进行了对比验证,结果表明,下落时间变异系数最大值为4.41%,姿态水平度最小值为93.63%,两项数据与试验结果分别相差4.75%和3.66%,且物料成功合盖率为99%。该结果表明,响应面仿真试验能够有效地完成对工作参数的优化工作,为今后扣合式合盖装置的进一步优化和试验研究提供了参考依据。
后续的研究中,笔者拟使用神经网络与寻优算法相结合的方法对该合盖机构进行优化,并将优化结果与Box-Behnken试验结果进行对比,以进一步提升装置的作业效果。

