考虑弹性误差的渐开线圆柱齿轮半解析接触模型与传动精度分析

肖 康， 张 楚， 董惠敏， 毛范海

（1. 大连理工大学 机械工程学院， 辽宁 大连 116024；2. 大连海事大学 船舶与海洋工程学院， 辽宁 大连 116026）

传动误差是影响齿轮传动精度和动力学特性的重要因素，对传动误差进行高效、精准的建模与分析是提升齿轮传动性能的重要基础。

目前，国内外学者针对齿轮传动误差的建模方法做了大量研究，常用的建模方法有解析法、有限元法及半解析法。例如：文献[1-6]采用有限元法对齿轮的传动误差进行了分析，该方法的求解精度较高，但由于建模复杂且网格划分密集，求解计算时间较长。为了提高求解效率，文献[7-12]采用解析法建立了齿轮传动误差的计算模型，极大地缩短了求解时间，但对齿轮的结构弹性问题考虑不足，导致求解精度受限。为了在缩短求解时间的同时保证准确性，现阶段很多学者开始研究半解析方法在齿轮传动精度分析中的应用，如Dong等[13]采用半解析法建立了齿轮的传动模型，有效地提高了齿轮接触性能的求解效率。此外，在传动误差影响因素分析方面，Korta等[1]在有限元建模的基础上探究了不同质量的材料对齿轮静态传动误差曲线的影响；邹帅东等[7]在解析建模的基础上考虑了齿轮偏心的因素，研究了不同偏心程度对齿轮传动误差的影响；刘永平等[3]分析了负载、转速及轴线误差等因素对齿轮传动误差的影响。

然而，上述针对齿轮传动误差的研究均未考虑弹性误差。为此，本文以渐开线圆柱齿轮为研究对象，在半解析方法的基础上建立考虑弹性误差的齿轮接触模型，并结合变形协调条件和力平衡方程，研究弹性误差对传动精度的影响规律，旨在为渐开线圆柱齿轮的工程应用提供指导。

1 渐开线圆柱齿轮的误差齿面模型

根据渐开线圆柱齿轮齿面的生成原理，将齿廓误差与齿面方程相结合，建立误差齿面模型，从而为齿轮传动误差的有限元求解提供理论基础。

1.1 齿轮的齿面方程

根据渐开线齿面的生成原理，当一条曲线在空间中沿螺旋线方向匀速拉伸变换时，所形成的表面即渐开线圆柱齿轮的齿面。如图1所示，以渐开线斜齿圆柱齿轮（后文简称斜齿轮）为例，推导其渐开线螺旋面方程[14]，表示为：

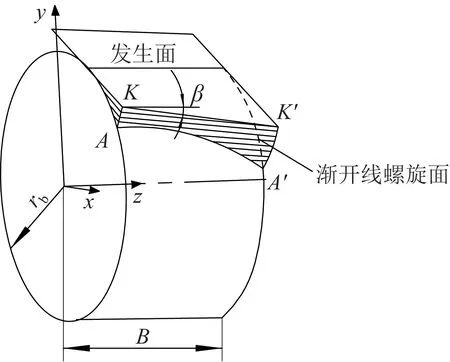
图1 渐开线螺旋面的生成Fig.1 Generation of involute helical surface

式中：rb为齿轮的基圆半径，θ为母线绕轴线的旋转角度，p为螺旋线参数，uk为渐开线发生角。

设渐开线圆柱齿轮的直母线与圆柱在x轴上的切点为s，在该直母线上存在一个动点k，令k点到s点的距离为l，直母线与端截面的夹角为α，则直母线的参数方程可表示为：

将直母线方程代入式(1)，得到渐开线圆柱齿轮的齿面方程：

1.2 齿轮的误差齿面方程

渐开线圆柱齿轮的齿廓误差具体值可通过查表确定[15]。将渐开线圆柱齿轮的齿廓曲线离散成点，并计算得到齿廓上各点与齿轮中心的距离r。以齿廓各点与齿轮中心的距离r为横坐标，齿廓误差为纵坐标，构建考虑齿廓误差的齿廓曲线，如图2所示。

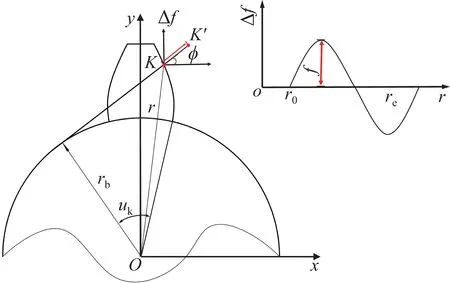
图2 考虑齿廓误差的齿廓曲线Fig.2 Tooth profile curve considering tooth profile error

根据图2，齿廓误差的表达式如下：

其中：

式中：Δf为齿廓离散点K的齿廓误差，f为齿廓误差最大值，r0为齿廓上第1 个离散点到齿轮中心的距离，re为齿廓上最后一个离散点到齿轮中心的距离，(xK,yK)为齿廓上任意离散点K的坐标。

如图2所示，以对应点的齿廓误差作为偏移距离，将齿廓离散点沿法线方向进行偏移，得到新的齿廓离散点K′ (x′K,y′K)。将新的齿廓离散点沿着螺旋线方向分布，即可得到误差齿面。添加误差后的齿廓离散点K′ (x′K,y′K)的坐标可表示为：

式中：ϕ为齿廓离散点K的法线方向与x轴的夹角。

2 考虑弹性误差的渐开线圆柱齿轮半解析接触模型

本文通过推导渐开线圆柱齿轮的变形协调方程、力平衡方程和提取柔度矩阵等来建立其半解析接触模型，以实现其传动误差的求解。

2.1 齿轮变形协调方程的推导

齿轮在传动过程中的接触可等效为弹性体的接触[16]，则主、从动轮接触线上每一个点的变形协调方程可表示为：

式中：Qi为接触点i的间隙，εi为由误差引起的初始接触间隙，包括齿廓误差、修形量等，Ui为接触点i因齿轮齿体的刚性运动而产生的位移，σi为接触点i处产生的弹性变形量。

在载荷的作用下，齿轮接触点处产生的弹性变形包括整体变形和局部接触变形，其中整体变形是指弯曲-剪切变形。渐开线圆柱齿轮的弹性变形可表示为：

式中：σhi为接触点i处的接触变形，σb1、σb2分别为主、从动轮的弯曲-剪切变形。

渐开线圆柱齿轮在某一位置处的接触问题可看作2个圆柱体的接触问题。在接触过程中，主、从动轮在接触点处的法向曲率半径为圆柱体的半径。根据统计接触理论[17]，在力作用下，接触点处的接触变形可表示为：

其中：

式中：Fi为接触点i处的载荷，N；li为接触点i所在接触线的分段距离，mm；μ1、μ2分别为主、从动轮的泊松比；E1、E2分别为主、从动轮的弹性模量，MPa；wi为接触点i对应的齿轮厚度，mm；Bi为接触半宽，mm。

渐开线圆柱齿轮的柔度矩阵包括整体柔度矩阵和局部柔度矩阵。则完整的柔度矩阵可表示为：

式中：λw为齿轮副的完整柔度矩阵；λb1、λb2分别为主、从动轮的弯曲-剪切柔度矩阵；λh为接触点的接触柔度矩阵。

渐开线圆柱齿轮的弹性变形量可表示为：

式中：σ为齿轮弹性变形量矩阵，F为接触点法向力矩阵。

在渐开线圆柱齿轮的啮合过程中，由于受到齿轮六自由度运动的影响，使得接触线上的点产生了刚性位移。通过构建投影矩阵，将齿轮的刚性位移投影到接触线的法线方向上，则齿轮啮合过程中产生的刚性位移可表示为：

式中：U为齿轮刚性位移在接触线法线方向上的投影量，G1、G2分别为主、从动轮的六自由度在接触线法线方向上的投影向量，Φ1、Φ2分别为主、从动轮的六自由度位移。

2.2 齿轮力平衡方程的推导

为了求解弹性变形影响下渐开线圆柱齿轮实际接触点的接触力，须建立主、从动轮的力和力矩的平衡方程。

当主动轮受到载荷作用时，需要主、从动轮之间的接触力和轴承支撑力来进行平衡。将主、从动轮之间的接触力投影到对应齿轮的坐标系下，则可得主动轮的受力平衡方程：

式中：T1为主动轮的外部载荷矩阵，F12为从动轮对主动轮的接触力，K1为主动轮的支撑刚度矩阵。

同理，可得从动轮的受力平衡方程：

式中：T2为从动轮的外部载荷矩阵，F21为主动轮对从动轮的接触力，K2为从动轮的支撑刚度矩阵。

将主、从动轮的受力平衡方程进行整合，可得到整体的受力平衡方程：

2.3 齿轮柔度矩阵的提取

由于主、从动轮的参数相同，只需在ANSYS软件中建立主动轮的完整和局部有限元模型，即可获取主、从动轮的弯曲-剪切变形系数[18]。以斜齿轮为例，其整体有限元模型采用五齿模型，如图3(a)所示。对齿轮中心孔处施加全约束，以获取整体柔度矩阵；轮体和齿体的弹性模量相同。斜齿轮局部有限元模型如图3(b)所示，对非接触齿面施加全约束，齿体弹性模量为齿面弹性模量的1 000 倍，以确保接触齿面仅包含局部接触变形。主、从动轮接触齿面上的节点坐标和单元完全一致。

主、从动轮接触齿面上节点的弯曲-剪切柔度系数矩阵可表示为：

式中：ηb,fe为接触齿面节点的弯曲-剪切柔度系数矩阵，ηt,fe为完整有限元模型的弯曲-剪切柔度系数矩阵，ηl,fe为局部有限元模型的弯曲-剪切柔度系数矩阵。

完成齿轮完整有限元模型和局部有限元模型的构建后，采用ANSYS 软件中自带的子结构法提取柔度系数矩阵[19]。但采用子结构法时会涉及外部节点和内部节点，由于本文不考虑内部节点的自由度，则可使用凝聚的方法忽略内部节点。将各子结构组装成整体时仅包含外部节点，其方程维数比原模型的方程维数小得多。

采用形函数插值运算方法对所构建的柔度矩阵进行运算，获得齿面接触点的弯曲-剪切柔度矩阵。对于任意网格节点，在确定齿面接触点与网格节点的位置关系后，通过已知的柔度系数插值获得接触点的柔度系数。不同齿面上接触点的柔度矩阵可通过齿面接触点与完整有限元模型的网格节点位置关系求得。最后按照接触点顺序，重新组装成柔度矩阵[20]。

2.4 考虑弹性误差的齿轮传动误差计算

基于上述建立的渐开线圆柱齿轮半解析接触模型，分析弹性误差对其传动精度的影响[21]，并构建齿轮传动误差的计算流程，如图4所示。

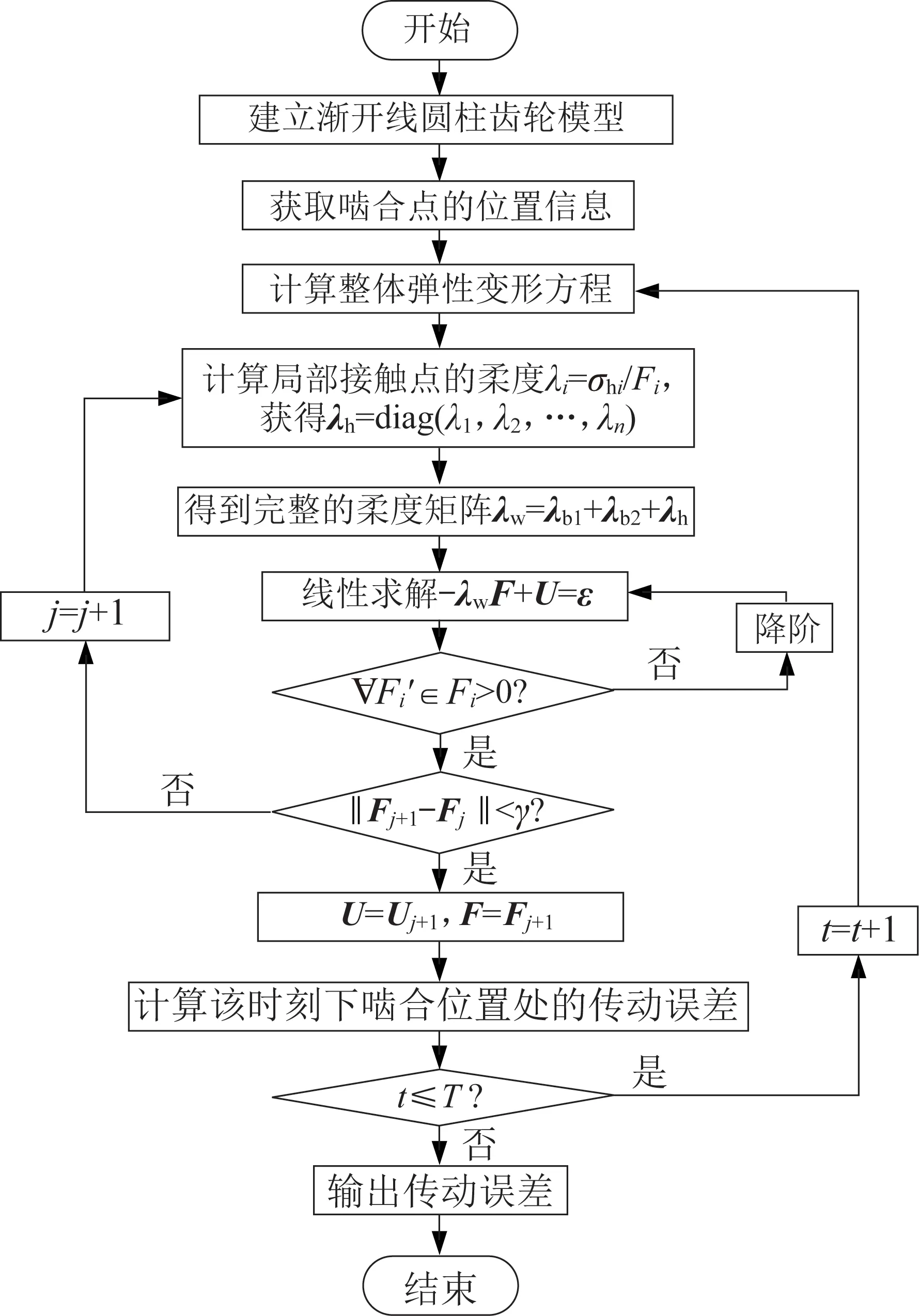
图4 考虑弹性误差的渐开线圆柱齿轮的传动误差计算流程Fig.4 Calculation process for transmission error of involute cylindrical gear considering elastic error

考虑弹性误差的渐开线圆柱齿轮传动误差的计算步骤如下：

1）首先根据齿轮的基本参数，建立齿轮几何模型，以计算得到齿轮接触线的位置，并对齿轮接触线进行离散化处理，获得均匀分布的离散点并确定其位置坐标。

2）基于所获得的离散接触点的坐标，考虑齿廓误差，每个接触点对应的齿廓误差幅值由接触点到齿轮中心的距离来确定，将得到的齿廓误差幅值代入接触间隙，并结合初始离散接触点的坐标，得到新的接触点坐标。

3）假设初始载荷对所有潜在接触点的作用相同，从而获得各接触点处的位移以及整体柔度矩阵和局部接触柔度矩阵，进而整合得到齿轮副的完整柔度矩阵。

4）根据接触点的接触力，判断该接触点是否参与啮合：Fi＜0 N表示接触点不参与啮合，Fi＞0 N表示接触点参与啮合。通过迭代得到所有参与啮合的接触点，并更新柔度矩阵。

5）通过‖‖Fj+1-Fj＜γ（j为迭代次数，γ为收敛容差）来判断结果是否收敛，若不满足收敛条件，则进行第2次迭代，直至得到最终的方程解。

6）基于获得的方程解计算该时刻下齿轮的传动误差，并基于上述步骤计算下一时刻的传动误差，直到获得一个啮合周期T内的传动误差后计算结束，同时输出最终的传动误差结果。

3 基于半解析模型的渐开线圆柱齿轮传动精度分析

3.1 半解析模型验证

为验证上文所构建的渐开线圆柱齿轮半解析接触模型的准确性，根据表1所示的斜齿轮参数进行实例分析，并将基于半解析模型和有限元法的传动误差计算结果进行对比。

表1 斜齿轮的基本参数Table 1 Basic parameters of helical gear

在ANSYS软件中建立一对斜齿轮的接触模型，2 个齿轮在节点处刚好接触；在从动轮转动中心点处施加全约束，主动轮仅保留绕z轴方向的转动，在主动轮转动中心点处施加300 N·m 的转矩，求解结束后直接提取主动轮在1个啮合周期内的传动误差。同时，利用半解析模型计算该齿轮副在1个啮合周期内的传动误差，并与有限元仿真结果进行对比。基于不同方法的斜齿轮传动误差随转动角度的变化曲线如图5所示。

图5 基于不同方法的斜齿轮传动误差对比Fig.5 Comparison of transmission error of helical gear based on different methods

由图5 可知，在1 个啮合周期内，基于有限元仿真和半解析模型的斜齿轮传动误差的变化曲线基本一致。2 种方法中斜齿轮模型在初始时刻下均处于同一个位置，同一时刻下齿轮传动误差的最大相对误差为5.8%，最小相对误差为3.2%，均在6%以内，验证了半解析建模方法的准确性。此外，半解析模型的求解时间为2.05 min，有限元仿真的求解时间为165 min，相比之下，半解析模型的求解速度提升了79.57 倍，表明半解析方法在求解效率方面具有极大优势。

3.2 齿廓误差对齿轮传动精度的影响

为分析齿廓误差对渐开线圆柱齿轮传动精度的影响规律，选用四级齿廓误差，在主动轮中心节点处施加300 N·m 的转矩，齿轮接触的初始位置为节点（齿廓接触点的公法线与连心线的交点）处，基于半解析模型计算有无齿廓误差情况下斜齿轮在1个啮合周期内的传动误差，结果如图6所示。

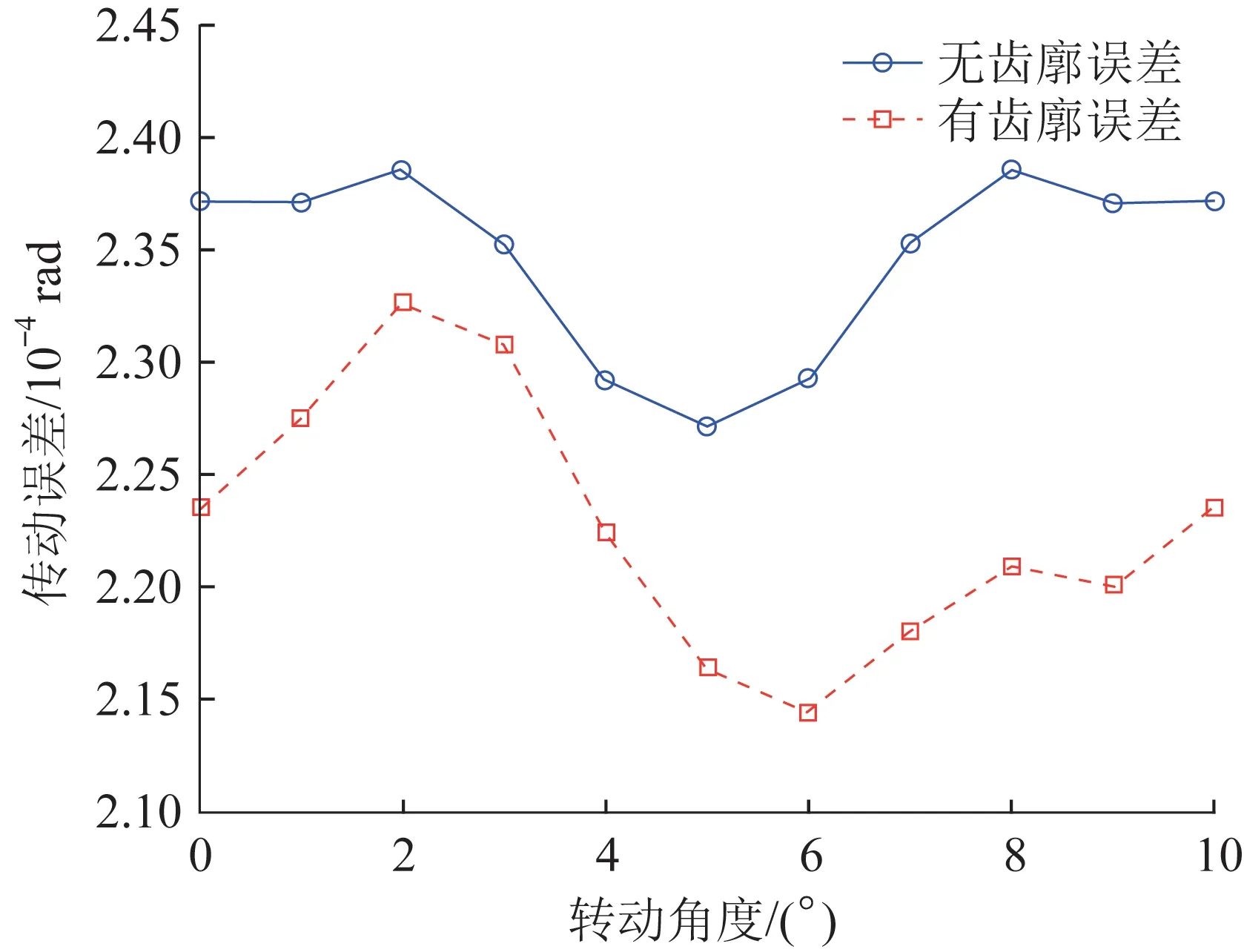
图6 齿廓误差对斜齿轮传动误差的影响Fig.6 Ⅰnfluence of tooth profile error on transmission error of helical gear

由图6可知，在无齿廓误差的情况下，斜齿轮的传动精度为1.133 0×10-5rad；在有四级齿廓误差的情况下，齿轮的传动精度为1.818 6×10-5rad。在有齿廓误差的情况下，斜齿轮的传动精度变大，由此可看出，齿廓误差会影响齿轮的传动精度。

3.3 载荷对齿轮传动精度的影响

不同载荷下齿轮的传动精度也不同。为了研究载荷对渐开线圆柱齿轮传动精度的影响规律，在斜齿轮存在四级齿廓误差的基础上，分别施加100，200，300，400 N·m 的转矩，基于半解析模型计算不同载荷下斜齿轮的传动误差，结果如图7所示。

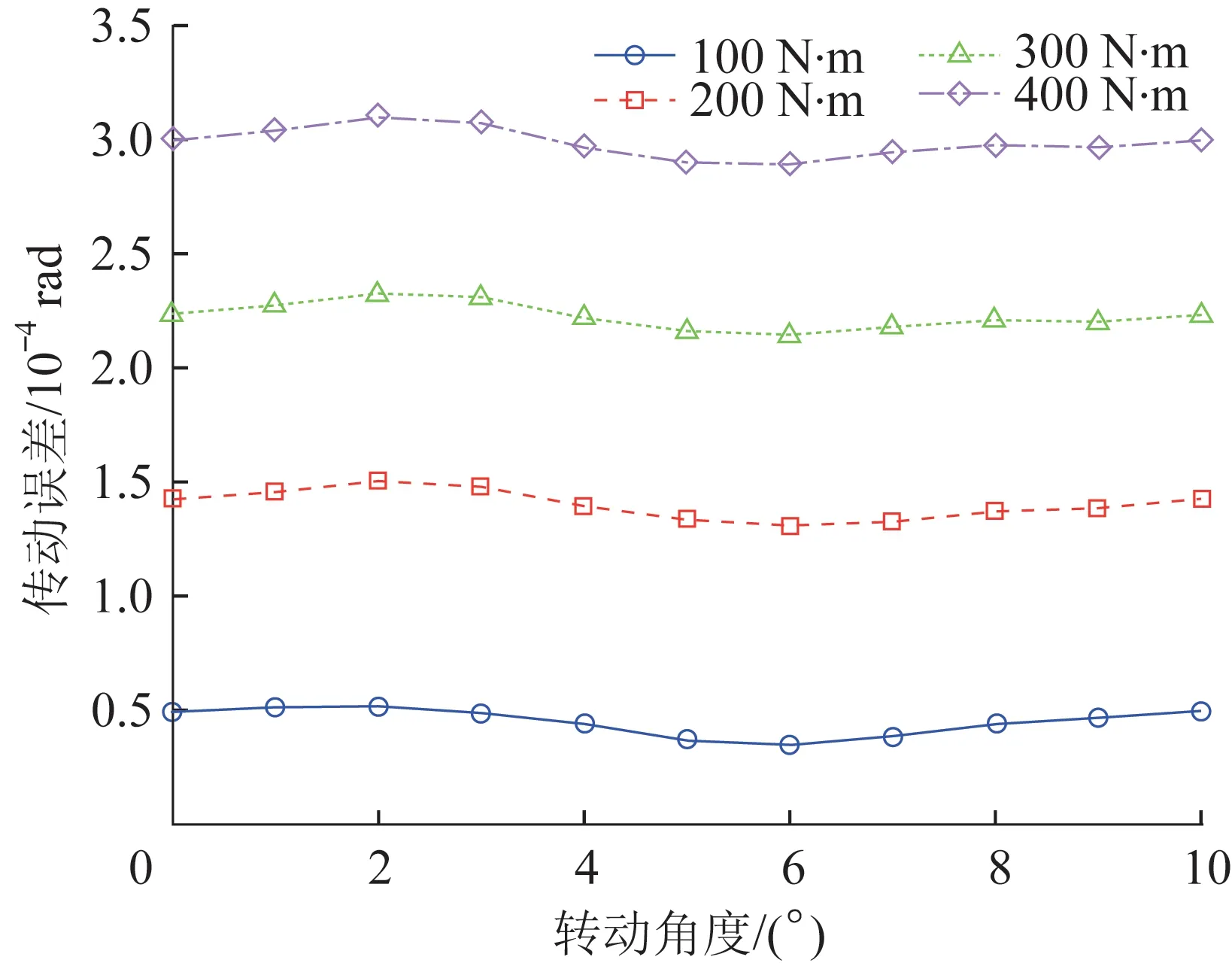
图7 载荷对斜齿轮传动误差的影响Fig.7 Ⅰnfluence of load on transmission error of helical gear

从图7中可以看出，在100，200，300，400 N·m转矩的作用下，斜齿轮的传动精度分别为1.68×10-5，1.95×10-5，1.82×10-5，2.05×10-5rad；随着载荷的增大，斜齿轮接触时的传动误差增大，且对应的传动精度也增大，说明载荷会对齿轮的传动性能产生较大的影响。

3.4 齿廓误差等级对齿轮传动精度的影响

为探究不同等级齿廓误差对渐开线圆柱齿轮传动精度的影响规律，基于半解析模型分别对无齿廓误差、四级齿廓误差和五级齿廓误差情况下（主动轮中心节点处施加300 N·m 转矩）斜齿轮传动误差的变化情况进行分析，结果如图8所示。

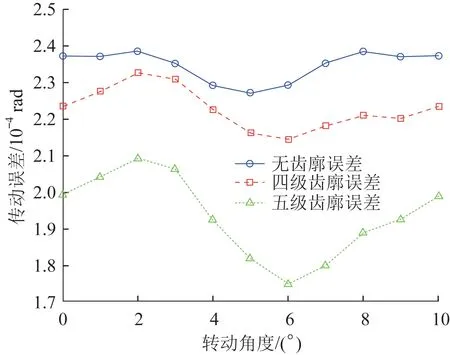
图8 齿廓误差等级对斜齿轮传动误差的影响Fig.8 Ⅰnfluence of tooth profile error level on transmission error of helical gear

由图8 可以看出，随着齿廓误差等级的变大，斜齿轮的传动精度也增大。在无齿廓误差的情况下，由于斜齿轮只受到载荷的影响，其传动精度的变化最小。当存在四级齿廓误差时，由于斜齿轮受到载荷和齿廓误差的综合影响，相对于无齿廓误差的情况下，其传动精度的变化较大。当存在五级齿廓误差时，由于斜齿轮的齿廓误差变大且同时受到载荷的作用，其传动精度的变化最大，且齿廓误差对齿轮的传动平稳性也有较大的影响。

4 结 论

本文结合有限元法和解析法的优点，建立了考虑弹性误差的渐开线圆柱齿轮半解析接触模型，并通过与传统有限元法的结果进行对比，验证了所构建的半解析模型的正确性。结果表明，半解析方法可有效提高渐开线圆柱齿轮传动精度的求解效率，与传统有限元法相比，本文方法的求解速度提升了79.57倍，且求解准确性较高。同时，基于所构建的半解析模型分析了不同载荷和齿廓误差等级对渐开线圆柱齿轮传动精度的影响规律，为渐开线圆柱齿轮的工程应用提供了指导。