环境风载荷下大口径反射面天线波束指向分析
栾 天, 薛 松,, 连培园,, 余佳恒, 杜雨轩, 王 猛, 赵武林,卢 波, 许 谦, 王从思
(1. 西安电子科技大学 机电工程学院,陕西 西安 710071; 2. 西安电子科技大学 广州研究院,广东 广州 510555;3. 陕西黄河集团有限公司,陕西 西安 710043; 4. 中国电子科技集团有限公司 第三十九研究所,陕西 西安 710065;5. 湖北省鄂州市天元砂辊有限责任公司,湖北 鄂州 436001; 6. 中国科学院 新疆天文台,新疆 乌鲁木齐 830011)
随着天文学的发展,人类对深空领域的探索不断深入,要求反射面天线能够接收来自太空的极为微弱的电磁信号。为了提高观测性能,反射面天线不断朝着大口径、高频段、高指向的方向发展[1]。随着反射面天线口径的不断增大,其刚度有所降低,环境载荷(如重力、温度和风等)对反射面天线结构变形的影响逐渐变大。由于重力、温度均属于缓变载荷,可通过提前估计其对天线的影响来进行变形补偿[2]。但是,风载荷具有时变性、不确定性等特性,如何快速评估风载荷下大口径反射面天线结构的变形及其对波束指向特性的影响成为研究关键[3]。
现阶段,国内外学者主要采用2种方法来消除风载荷对大口径反射面天线变形的影响。第1种方法是安装天线罩。例如:麻省理工学院的Olmi等[4]为Haystack天文台的37 m口径的射电望远镜安装了天线罩,以减小风载荷对天线变形的影响。第2种方法是采用伺服控制系统来调整天线的指向,从而减小风载荷的影响。Kim等[5]将天线视为理想刚体,通过仿真分析验证了模糊PⅠD(proportional-integral-differential,比例-积分-微分)控制相较于传统控制方法的优越性。Gawronski[6]针对美国国家航空航天局的深空网络天线控制系统,验证了PⅠ(proportional-integral,比例-积分)控制算法的可靠性,但存在对高频段控制效果不佳的问题;此外,还证明了LQG(linear quadratic Gaussian,线性二次高斯)控制和H∞算法能够提高天线伺服控制系统的传动性能,但因受到硬件的限制,控制效果不太理想。Lin等[7]将PⅠD控制与模糊理论相结合,用于改善天线的动态性能,该方法的控制效果较好。Tang 等[8]分析了PⅠ控制、LQG 控制、DFF(disturbance feed forward,扰动前馈)控制和DOBC(disturbance observer-based control,基于干扰观测器的控制)下天线抗风扰的效果,结果表明,DOBC对风扰的抑制效果最好。
然而,上述针对天线伺服控制的研究通常将天线的反射面假设为刚性,即不考虑反射面的柔性变形,并将天线视为整体进行控制。但对于大口径反射面天线,其反射面表面的结构变形对波束指向的影响不能忽略,因此须对反射面的变形机理进行研究。现阶段,天线反射面风载特性的研究方法主要包括理论分析、数值模拟、风洞试验以及现场实测等。因受制于成本、普适性和实验难度等,数值模拟是目前最常用的技术手段。数值模拟是指利用CFD(computational fluid dynamics,计算流体动力学)方法,通过计算机对物体的风载特性进行仿真分析,其优势是计算成本低、不受尺寸限制,且可以较方便地获得不同工况下的风载特性[9]。Young等[10]针对风载荷对双子座望远镜的球形保护罩的影响进行了数值模拟,结果表明,不同风场环境下球形保护罩的风载特性不同。Du等[11-12]对相控阵雷达的风载特性进行了数值模拟。王春圆、刘岩等[13-14]对大型射电望远镜的风载特性进行了数值模拟,并通过与风洞试验结果进行对比来验证数值模拟的准确性。Ladd 等[15]对GMT(giant Magellan telescope,巨型麦哲伦望远镜)进行了CFD数值模拟,所得结果可为望远镜的结构设计、选址提供参考。综上,国内外学者虽已利用数值模拟及风洞试验等方法对大口径反射面天线的风载特性进行了分析,但对其面形精度和波束指向特性等的分析较少。
为此,笔者以奇台射电望远镜(Qitai radio telescope, QTT)的110 m 大口径反射面天线为研究对象,利用CFD数值模拟方法来分析和计算风扰情况下天线反射面表面的风压系数和变形情况,并结合天线结构的变形情况对其波束指向特性的变化规律进行研究,旨在为大口径反射面天线的抗风结构设计与系统控制研究提供理论指导。
1 大口径反射面天线风场的数值模拟
CFD数值模拟具有控制方便、成本低、易模拟各种环境、可重复操作以及可获得丰富的可视化信息等优点,常被用于大型结构的风场研究[16]。CFD数值模拟流程主要分为三部分:前处理、求解和后处理,具体如图1所示。
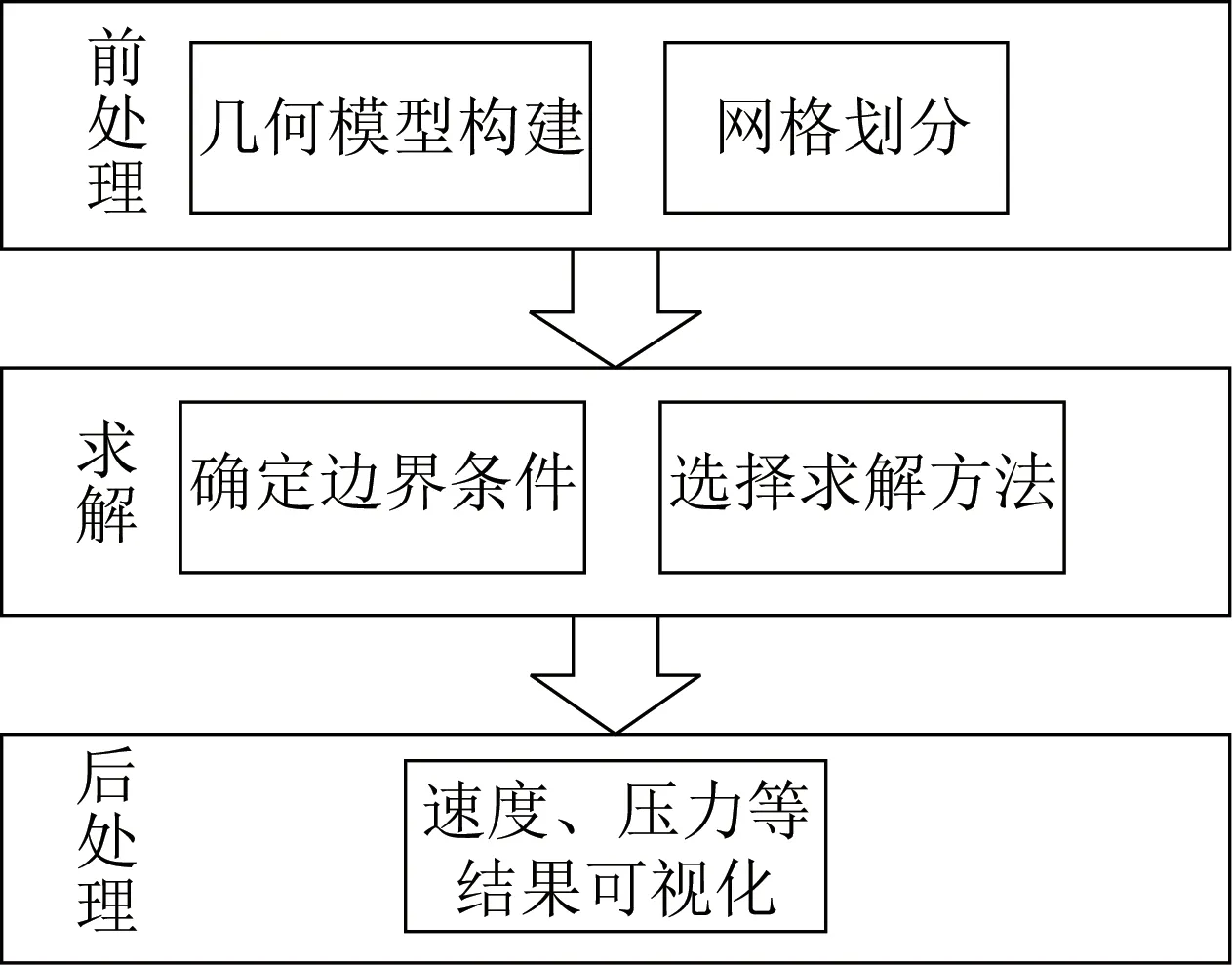
图1 CFD数值模拟流程Fig.1 CFD numerical simulation process
根据图1所示流程,首先采用Space Claim软件对QTT 的110 m 大口径反射面天线进行风场建模,然后采用Fluent软件对天线反射面表面的风压分布情况进行数值模拟,最后使用Tecplot软件对天线反射面表面的风压系数进行可视化后处理。
1.1 天线计算域模型的构建
由于受到网格生成方法的限制,在天线桁架杆件处无法有效划分出合适的网格,且反射面的背架结构对反射面风压分布的影响较小,故在划分网格时,忽略背架结构,仅建立天线反射面的抛物面模型,以分析其风压分布情况。计算域是指流体流经的区域,对于外部流动,计算域的边界应远离天线模型,以使湍流运动充分发展。若计算域尺寸过大,则会导致网格数量增加,从而造成计算量增大,这会大大降低计算效率,因此须对计算域模型的尺寸进行限制。
反射面天线计算域的尺寸参数包括高度H、上游尺寸L1、下游尺寸L2和宽度B等。为避免阻塞效应对天线结构周围的流场产生干扰,同时保证计算速度,通常要求阻塞率不大于3%。当天线反射面的直径为D时,根据文献[13]确定天线计算域尺寸,具体如下:
根据阻塞率的计算公式和上述尺寸参数,可得:
式中:γ为阻塞率。
由式(1)可知,阻塞率满足要求。基于上述尺寸参数,建立大口径反射面天线的计算域模型,如图2所示。
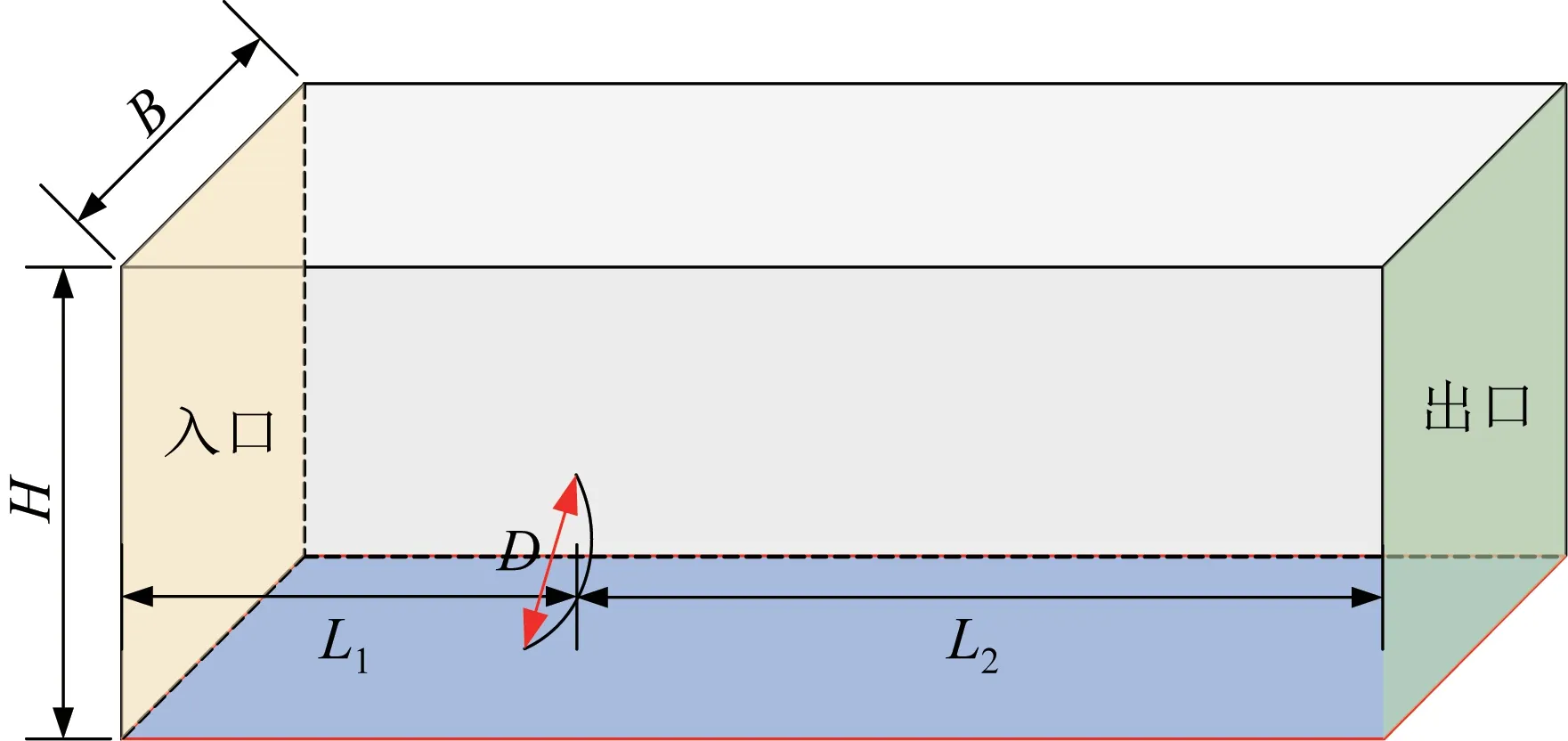
图2 大口径反射面天线计算域模型Fig.2 Computational domain model of large aperture reflector antenna
1.2 天线反射面表面风压系数的计算
在求解前,应对大口径反射面天线计算域模型设置合适的边界条件:入口设为风的速度入口,假设出口处所有物理变量的法向梯度均为零;计算域的上表面及2个侧面为滑动壁,计算域底面和天线反射面为非滑动壁。另外,在计算前还须对整个计算域进行网格划分。鉴于非结构化网格具有较好的自适应性,能够解决复杂流场的网格划分问题,本文采用非结构化网格单元对所构建的计算域模型进行网格划分。
RANS (Reynolds-averaged Navier-Stokes,雷诺平均湍流模型)通过引入合理的湍流模型来对雷诺应力项进行求解,该模型在求平均风压等方面具有明显优势[17]。鉴于SSTk-ω模型对近壁面的模拟精度较高,本文采用该湍流模型对天线的流固耦合问题进行求解。在SSTk-ω模型中,动能k、湍流耗散率ε和比湍流耗散率ω的计算式如下:
式中:uz为任一高度处的平均风速;Ti为任意点处的温度;Cμ为常数,常取0.09;l为湍流积分尺度。
利用Fluent软件对大口径反射面天线的网格模型进行求解,得到其反射面表面的风压分布情况。通常情况下,采用风压系数来描述风载荷对结构的力作用。结构表面风压系数Cp的计算式如下:
式中:p为作用在结构表面的风压,pref为参考点处的风压,ρ为流体密度,v为参考点处的风速。
天线反射面表面所受的实际压力为正、背面的压力差,则风压系数Cp可表示为:
式中:Cp_f、Cp_b分别为反射面正、背面的风压系数。
根据式(3)和式(4),通过CFD 数值模拟得到天线反射面表面的风压系数分布情况。由于天线反射面表面的风压系数与风速无关,因此仅计算某一风速下反射面表面的风压系数,即可获得不同风速下天线反射面的风载特性。为探究俯仰角变化对天线反射面风载特性的影响,对天线方位角为0°、俯仰角不同(分别为5°,15°,30°,45°,60°,75°,90°)的工况下反射面正、背面的风压系数进行计算,结果如表1所示。
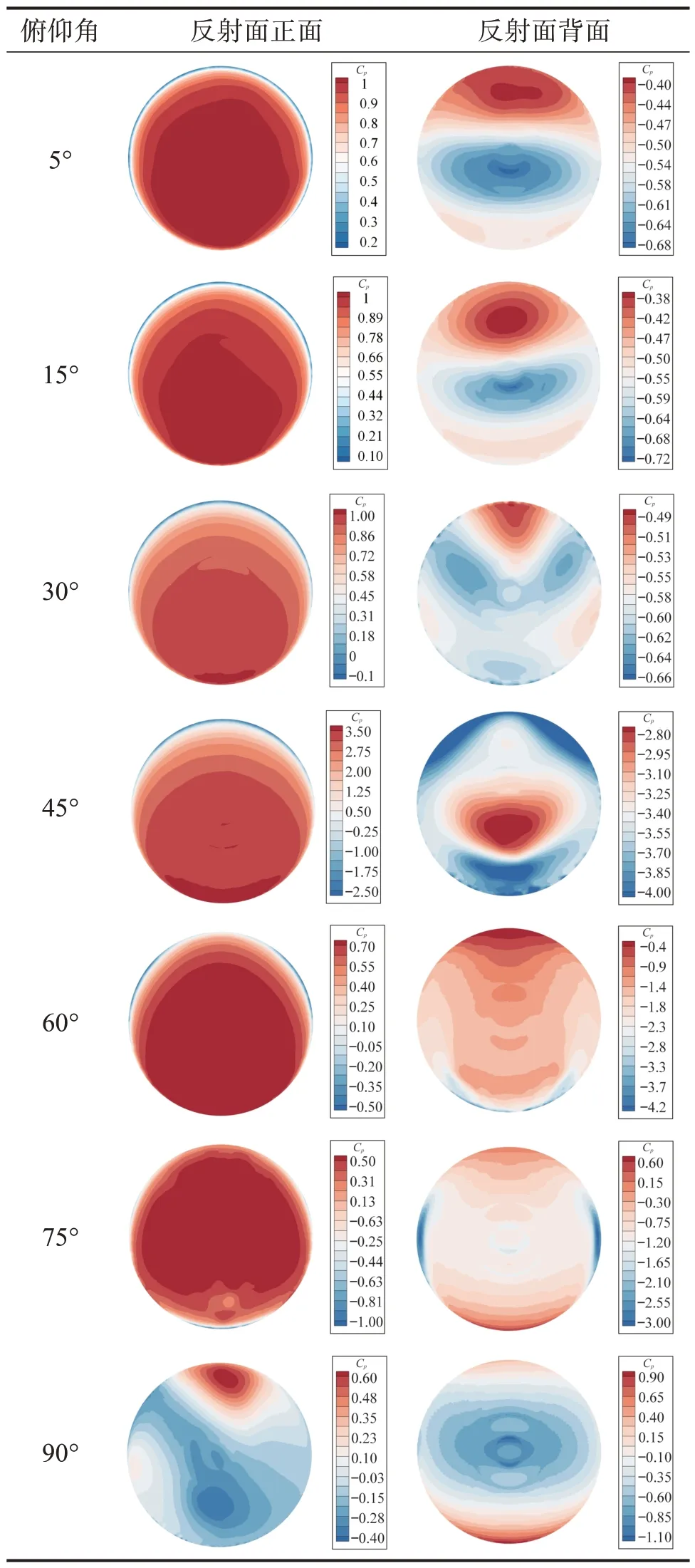
表1 不同俯仰角下天线反射面表面的风压系数Table 1 Wind pressure coefficient on antenna reflector surface under different pitch angles
由表1所示的天线反射面正、背面的风压系数分布情况可以看出,不同工况下最大变形均出现在反射面边缘,且多为迎风口边缘。这是因为来风在天线反射面的边缘被分开,迎风处反射面正面的风向上产生正压,背面的风向下产生涡流,形成负压,正、背面的作用效果叠加,产生较大风压。此外,在某些俯仰角工况下,风会在天线反射面的背面产生绕流,进而导致反射面边缘处的风压较大。
对天线反射面面板由内向外、按逆时针方向进行编号,由此得到不同反射面面板表面的风压系数随俯仰角的变化情况,如图3(a)所示。以天线俯仰角为75°的工况为例,详细展示天线第9 环、第16环反射面面板表面的风压系数,如图3(b)至图3(d)所示。由图3可以看出,天线反射面左右两侧边缘处的风压系数较大。
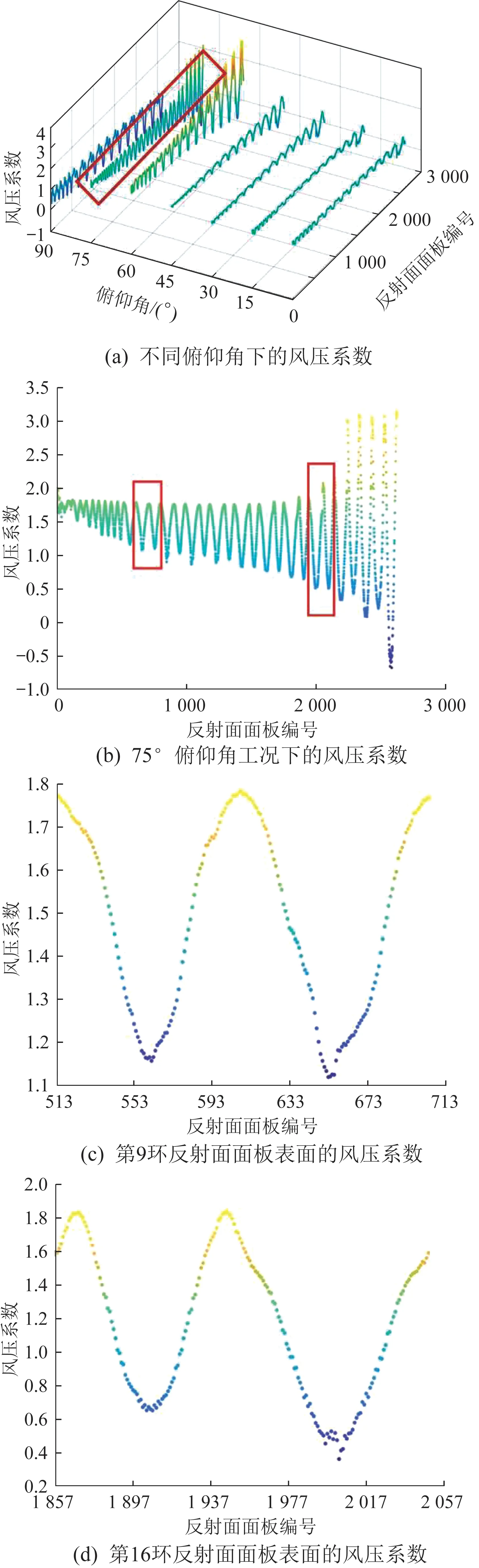
图3 天线反射面面板表面风压系数随俯仰角的变化趋势Fig.3 Variation trend of wind pressure coefficient on antenna reflector panel surface with pitch angles
2 大口径反射面天线结构变形及面形精度分析
2.1 天线结构变形的有限元分析
对于所研究的110 m 大口径反射面天线,本文只分析其反射面的流固耦合变形,即在有限元模型中将风载荷以风压的形式直接作用于反射面上,从而分析反射面的结构变形。为方便计算,分析时对天线的有限元模型进行简化,只建立反射面及背架结构的模型,将约束点设置在背架结构上,并在反射面上施加压力载荷。
鉴于直接利用天线反射面上网格节点处风压系数计算风载荷的过程非常复杂,为确定用于后文结构变形分析的风载荷值,拟对反射面进行区域划分。反射面表面的风压系数采用所有网格节点处的平均风压系数来近似表示,随后基于该平均风压系数来计算反射面所受的压力,并将压力平均分布至反射面面板的各个顶点上。图4所示为天线反射面表面的平均风压系数的近似计算示意。
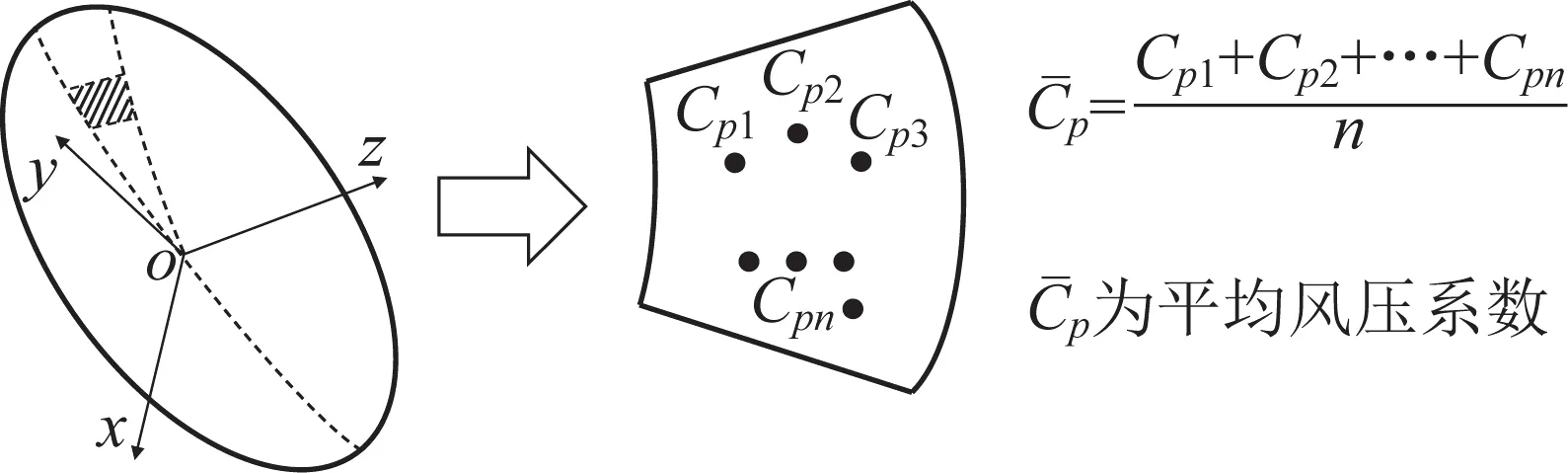
图4 天线反射面表面平均风压系数的近似计算Fig.4 Approximate calculation of average wind pressure coefficient for antenna reflector surface
根据平均风压系数,可以计算出每一块反射面面板上的均布载荷,其计算式如下:
式中:F为反射面面板所受的力,A为单一反射面面板的面积,Cˉp为反射面表面的平均风压系数。
在天线有限元模型中,将每一块反射面面板所受的载荷平均分布到4个顶点处,即可将流固耦合问题转换为静力学问题,通过静力学有限元分析可快速计算得到天线反射面的结构变形。
根据文献[18],大口径反射面天线选址一般选择风速较小处,QTT台址处风速不大于6 m/s(四级风)的比例为87.7%。基于此,以四级风为例,计算不同俯仰角工况下天线反射面的变形情况,结果如图5所示。
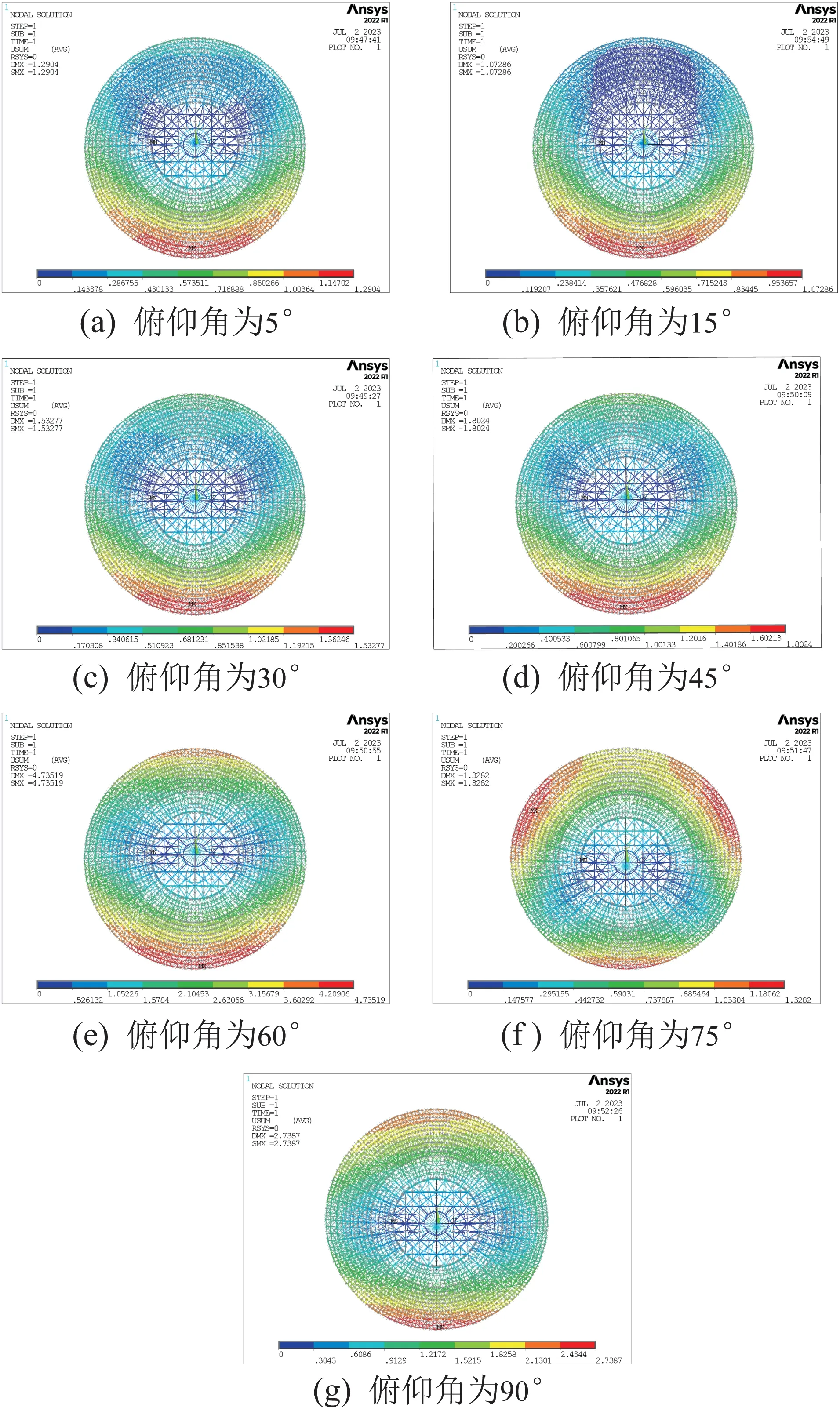
图5 不同俯仰角下天线反射面的变形情况Fig.5 Deformation of antenna reflector under different pitch angles
由图5可以看出,6 m/s风速下天线反射面变形的变化趋势与风压系数的变化趋势相对应;当俯仰角较小时,天线下端迎风口区域的变形量最大。
图6所示为6 m/s风速下天线反射面的变形极值随俯仰角的变化趋势。一般情况下,风压系数较大时,天线反射面的变形也较大。但由图6可知,俯仰角为90°时反射面表面的风压系数不大,而结构变形却较大。出现这一现象的原因如下:在其他俯仰角工况下,反射面表面的风压系数均为正值,而当俯仰角为90°时,风直接吹到反射面的背面,使得反射面表面上一部分的风压系数为负值,导致反射面受到了较强的倾覆力矩,从而产生了较大的变形。
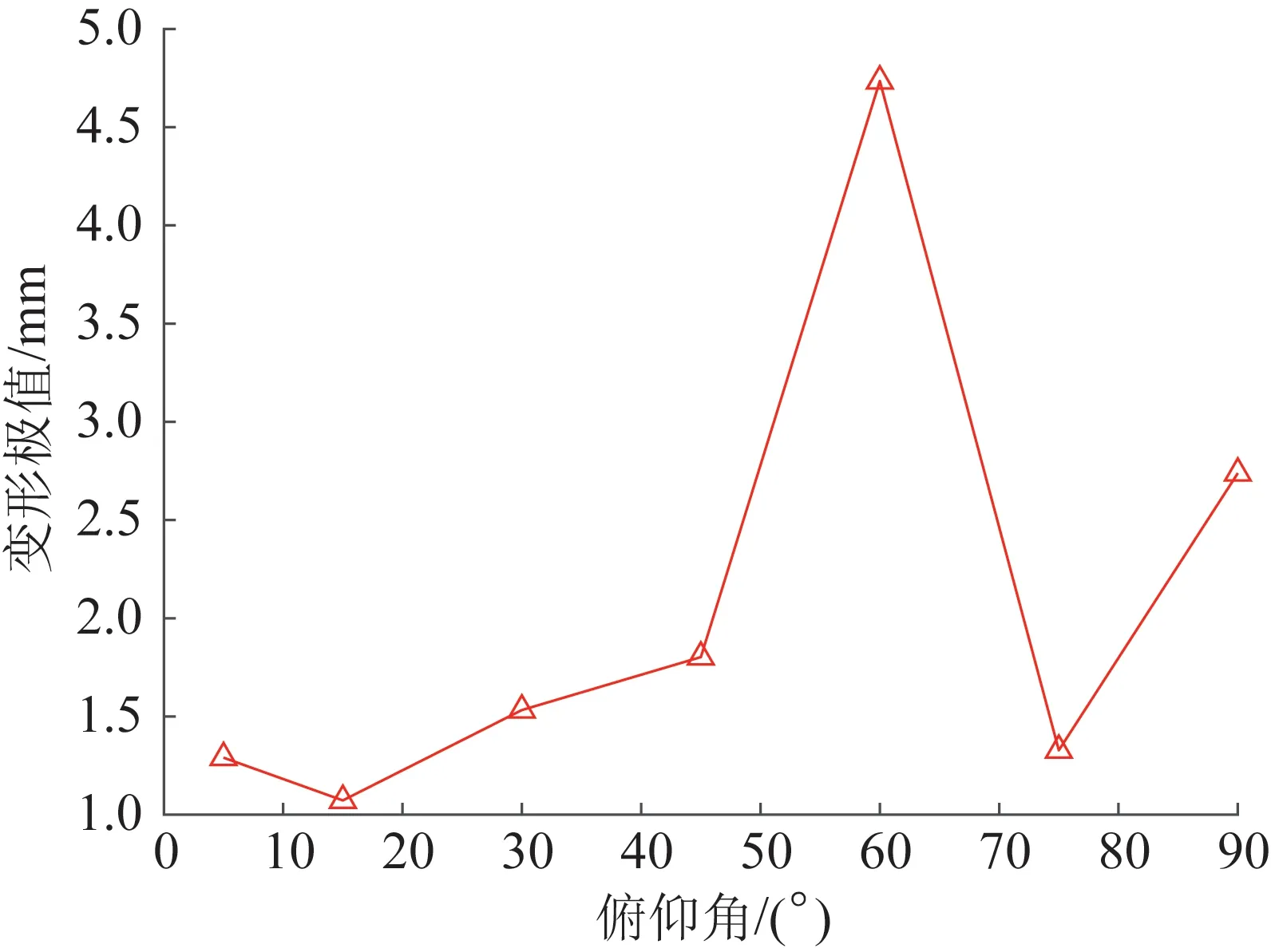
图6 不同俯仰角下天线反射面的变形极值Fig.6 Extreme value of deformation of antenna reflector under different pitch angles
2.2 天线面形精度分析
通常采用结构变形量的均方根误差(root mean square error, RMSE)作为衡量天线反射面变形程度的指标。对不同风速、俯仰角工况下天线反射面变形量的RMSE进行计算,结果如图7所示。
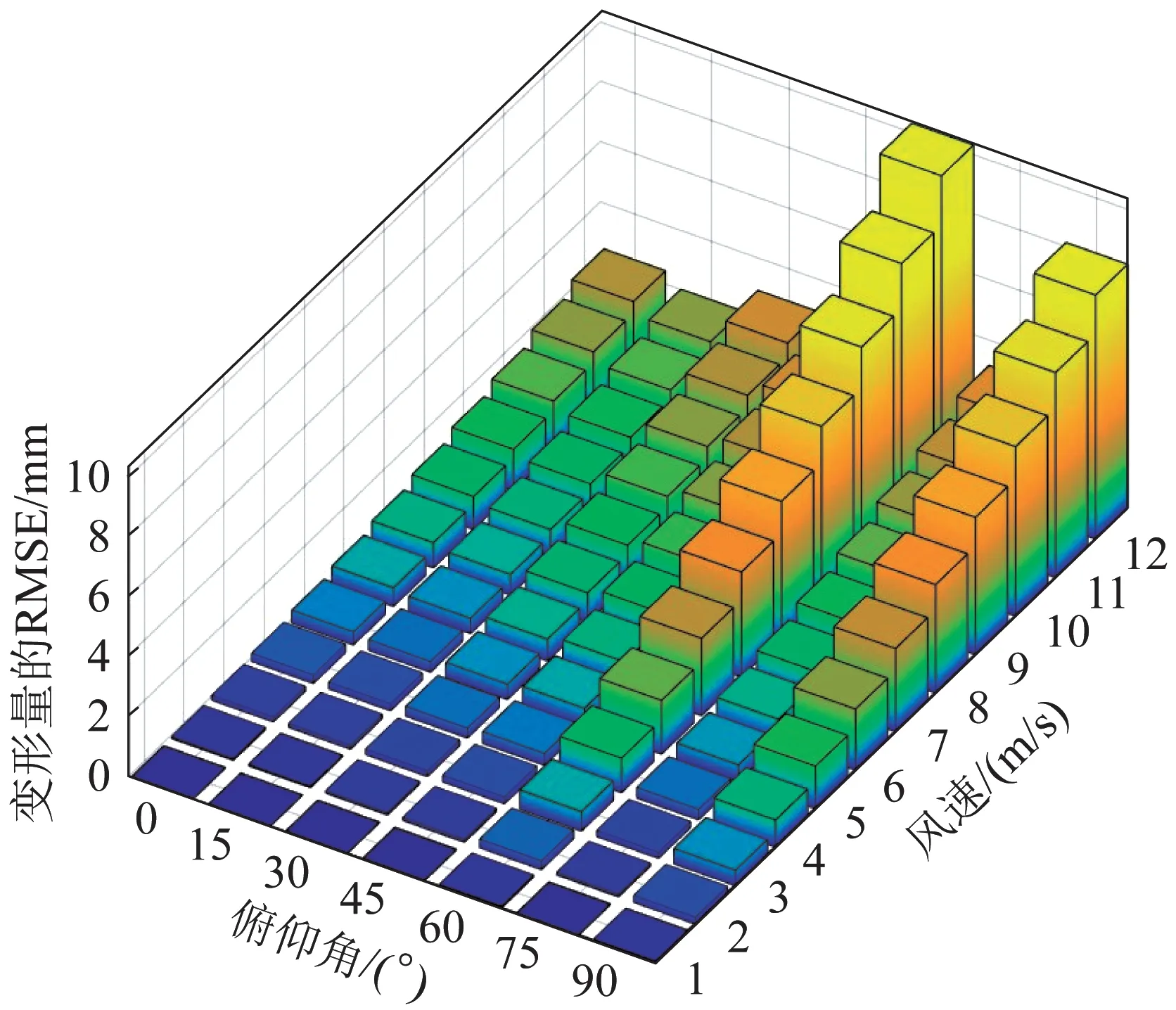
图7 不同风速、俯仰角下天线反射面变形量的RMSEFig.7 RMSE of antenna reflector deformation under different wind speeds and pitch angles
由图7可以看到,随着风速的提高,天线反射面变形量的RMSE 逐渐增大;在天线俯仰角为60°的工况下,反射面的变形较严重,应作为控制调节的关注重点。
3 大口径反射面天线波束指向分析
结构变形会影响天线的电性能,从而导致增益损失、指向偏差等问题。从天线的方向图中可以看出天线在空间各个方向上接收电磁波的能力。通过绘制不同工况下大口径反射面天线的方向图,即可得到其波束指向的变化情况。
文献[19-20]指出,物理光学法可以准确地分析大口径反射面天线主、副瓣的特性。为此,本文基于物理光学法,将反射面的变形转换为相位误差并引入到天线电性能的积分公式中,则反射面天线远区辐射电场的计算式可表示为:
其中:
式中:E为远区辐射电场,(θ,ϕ)为远场观测方向,h为自由空间波数,η为自由空间波阻抗,为等效面电流,r为远场观测点指向坐标原点的矢量,J为口径面等效面电流,δ为口径面的相位误差,σA为反射面在口径面上的投影面,Δz为轴向变形,θs为馈源坐标系os-xsyszs下反射面节点矢量与zs轴的夹角。
根据2.1 节,可以得到天线反射面上各点的径向位移。由于CFD数值模拟耗时较长,为了快速计算得到不同俯仰角、风速工况下天线电性能的变化,可先提前计算并存储反射面表面的风压系数,随后即可快速计算得到相应风速下反射面的结构变形量,最后根据变形量得到天线的方向图,以分析其波束指向特性。大口径反射面天线波束指向的分析流程如图8所示。
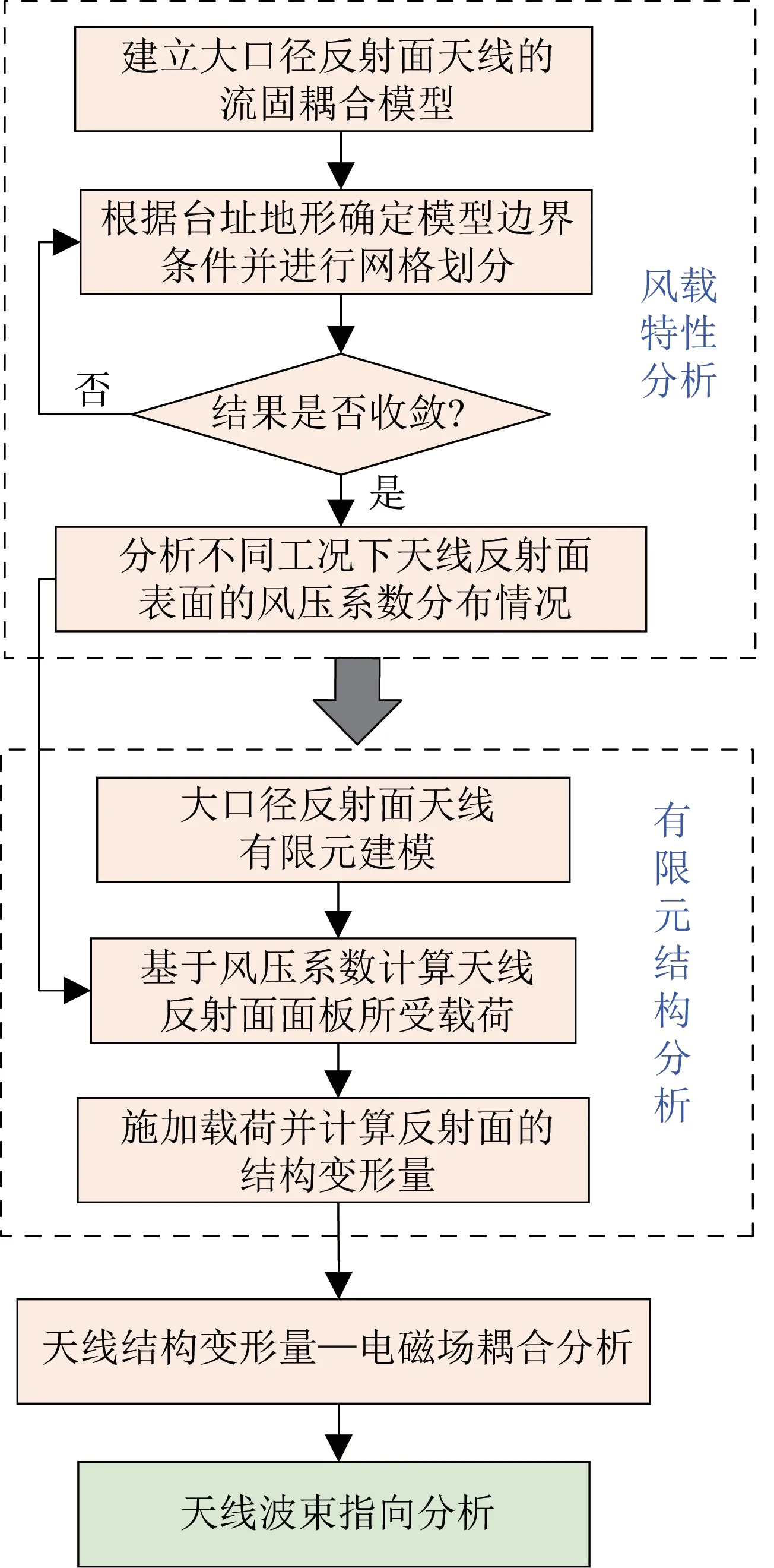
图8 大口径反射面天线波束指向分析流程Fig.8 Analysis process for beam pointing of large aperture reflector antennas
利用文献[21]中的方法,对式(6)的指数误差项ejδ进行分段线性拟合,从而得到变形后天线的方向图。图9 所示为不同俯仰角工况下四级风(6 m/s)正吹时天线的方向图。图中:E面表示平行于电场方向的平面,H面表示平行于磁场方向的平面。由图9可以看到,天线的电性能随俯仰角的变化而变化,且变化程度与反射面的结构变形有关。从E面方向图中可以看出,天线的增益损失较大,从H面方向图中可以看到,天线的波束指向偏差较大。
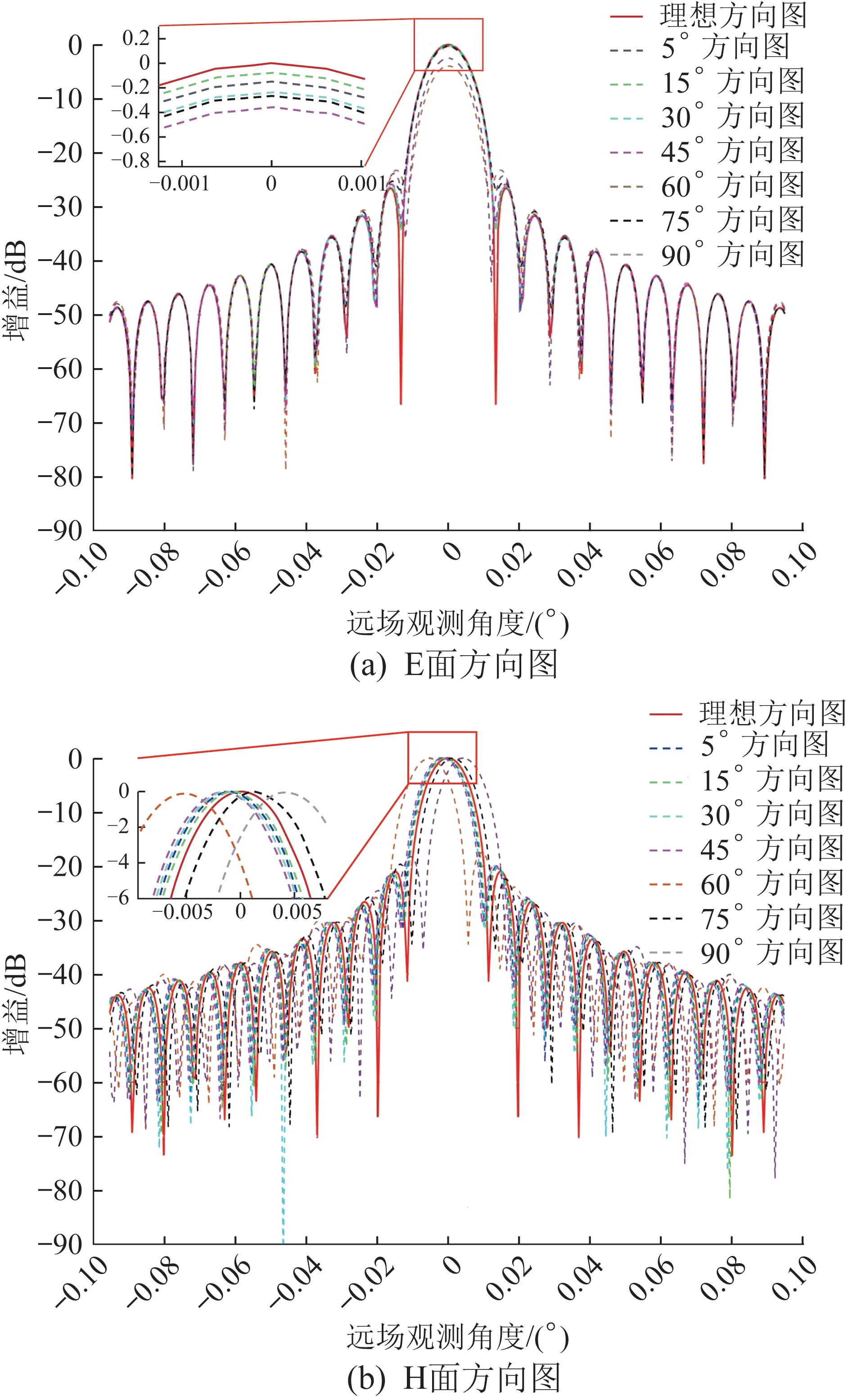
图9 6 m/s风速下天线的方向图Fig.9 Directional pattern of antenna at 6m/s wind speed
图10 所示为6 m/s 风速下天线的增益损失随俯仰角的变化趋势。从图10中可以看出,天线的增益损失与反射面的结构变形呈正相关;在不同俯仰角工况下,反射面的结构变形越大,天线的增益损失越严重,则其观测性能越差。
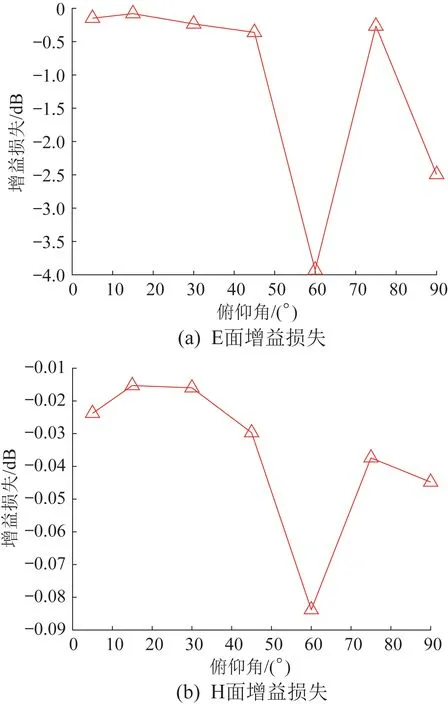
图10 6 m/s风速下天线的增益损失Fig.10 Gain loss of antenna at 6 m/s wind speed
当天线在工作时,若其副瓣电平抬高,则会导致主瓣的能量降低,这不利于天线接收信号。天线副瓣电平越低,表示其抗干扰的能力越强。图11所示为6 m/s风速下天线第一副瓣电平随俯仰角的变化情况。从图11中可以看到,在增益损失较大的不利工况下,天线第一副瓣电平会抬高,导致天线的观测性能下降。

图11 6 m/s风速下天线第一副瓣电平的变化情况Fig.11 Variation of the first sublobe level of antenna at 6 m/s wind speed
4 结 论
本文采用CFD 数值模拟方法分析了大口径反射面天线表面风压系数的分布情况,从而得到了其风载特性。随后,利用风压系数计算了天线各反射面面板所受的风载荷,并对天线进行有限元仿真分析,得到了天线的结构变形规律。最后,通过天线结构变形量—电磁场的耦合计算,得到了其反射面波束指向特性的变化情况。具体结论和建议如下:
1)天线反射面迎风口处所受的风压较大,且此处的变形较大,在后续的柔性控制中应重点关注。
2)某些工况下天线的结构变形和波束指向偏差较大,故不同工况的控制应具有针对性。
3)由于天线的结构复杂,本文仅考虑了反射面的变形情况,后续研究应综合考虑其他结构的变形。
通过分析大口径反射面天线的风载特性可以快速计算得到其反射面的结构变形以及电性能的变化情况,这可为天线的风扰控制提供参考。

