一种锚索框架梁内力计算新方法及现场试验

李京榜,朱彦鹏

(1.兰州工业学院 土木工程学院,甘肃 兰州 730050; 2.兰州理工大学 甘肃省土木工程防灾减灾重点实验室,甘肃 兰州 730050; 3.西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州 730050)

锚索框架梁作为一种新型柔性支护结构,在高边坡支护工程中得到了广泛应用[1-2]。进行框架梁设计时,基于Winkler弹性地基梁理论的计算方法考虑了框架梁和岩土体之间的相互作用,计算结果更加接近实际工程,因而得到了广泛的应用和发展。许英姿[3]选取Winkler弹性地基模型,仅考虑纵梁对荷载的传递作用,对框架梁进行了内力和变形的分析。宋从军[4]选取弹性半空间地基模型进行框架梁的内力计算,提出需要按张拉阶段和工作阶段分别计算框架梁内力。周志刚[5]将框架梁视为作用在双参数弹性地基上的梁对其内力进行求解,推导了双参数地基梁的初参数法。针对框架梁的试验研究也取得了一定的成果,陈春丽[6]以框架梁加固黄土边坡为对象进行了室内缩尺模型试验,研究了锚杆抗剪作用的内力分布规律,揭示了框架锚固体系的力学抗滑机制。Winkler弹性地基梁理论计算简单,其计算结果一定程度上可以满足工程应用,但计算结果偏于保守,有待进一步的优化。

本文依托工程实例,引入“换算截面”的概念对基于Winkler弹性地基梁理论的计算方法进行优化,给出框架梁内力的解答,并结合现场试验,对理论计算结果进行对比验证。本文的研究考虑了框架梁与岩土体之间的相互作用,反映了框架梁的实际受力情况,可为类似高边坡预应力锚索框架梁的设计和试验提供参考。

1 锚索框架梁内力分析

1.1 Winkler弹性地基梁理论

进行边坡支护结构的框架梁设计时,常采用Winkler弹性地基梁理论[7],将地基土看作线弹性体,假定地基土表面任一点的沉降与该点所受的压力强度成正比[8],即

p(x)=ks,

(1)

式中:p(x)为基底反力;k为基床系数,可根据场地岩土体性质或现场测试确定;s为地基的沉降量。

ω=eλx(C1cosλx+C2sinλx)+

e-λx(C3cosλx+C4sinλx)+ω1(x),

(2)

(3)

式中:λ为梁的柔度特征值;C1、C2、C3、C4均为待定积分常数,可由荷载及边界条件确定。

此时,框架梁可拆分为若干根横梁和竖梁,每根梁均为有限长梁,锚索的锚固力可简化为作用在梁上的集中力,且一根梁上常有多个锚固力作用,最终利用叠加法即可求解框架梁任一截面所受的内力[7]。

1.2 框架梁截面惯性矩分析

采用1.1所述方法计算框架梁内力时,λ是衡量框架梁抗弯刚度大小的一个重要指标,λ越小,梁的抗弯刚度越大,即梁抵抗弯曲变形的能力越强。由式(2)可知,当框架梁的材料及尺寸确定,且地基的基床系数k已知时,框架梁截面惯性矩I是影响λ的唯一因素。

传统方法常将框架梁看作单一材料,按照材料力学中一般矩形截面惯性矩的计算方法进行求解[9],即

(4)

式中:I为梁的截面惯性矩;b为梁的宽度;h为梁的高度。

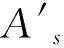
(5)

式中:h0为梁截面有效高度;a′为受压区钢筋保护层厚度;x0为换算截面中和轴高度。

2 工程算例

2.1 工程概况

春长路高边坡位于甘肃省舟曲县老城区春长南路东侧,坡脚紧邻一条城市道路,道路另一侧为居民生活区域,边坡现场照片见图1。该边坡加固设计安全等级为一级,边坡土层分布见表1。该边坡北侧治理高度为48.5 m,设计坡度为41.3°,坡脚处修建浆砌石挡墙,高3.0 m;挡墙以上采用预应力锚索框架梁对其进行加固。每榀框架梁由3根横梁(自下往上为边横梁H1,中横梁H2,边横梁H3)和3根竖梁(从左往右为边竖梁S1,中竖梁S2,边竖梁S3)组成,框架梁截面均为0.3 m×0.3 m的矩形截面,其平面尺寸如图2所示;锚索与水平面夹角20°,锚固力锁定值为230 kN。

图1 加固前边坡现场

表1 边坡土层分布

图2 框架梁示意(单位:mm)

2.2 计算假定

计算时,将框架梁拆分为横梁和竖梁,并考虑边坡岩土体与框架梁相互作用。本文主要分析锚索框架梁在张拉阶段的受力状态,为简化计算,作以下假定:

1) 不考虑框架梁自重,忽略顶梁和基础对框架梁的影响;

2) 不考虑预应力锚索沿坡面方向的分力对框架梁的影响;

3) 不考虑框架梁节点处横梁和竖梁之间扭转的相互影响;

4) 假定框架梁和边坡岩土体之间光滑接触。

在上述条件下,张拉阶段锚索框架梁力学模型见图3。

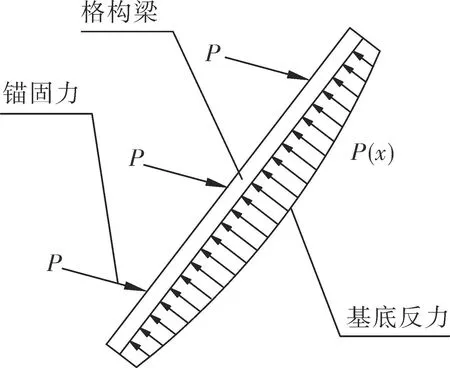
图3 张拉阶段锚索框架梁力学模型

2.3 框架梁内力结果分析

采用本文所述方法分别计算横梁H2和竖梁S2在设计锚固力作用下的内力值,其中,梁的截面惯性矩分别采用传统方法和换算截面法确定。其中,框架梁弯矩的计算结果见图4。

由图4可知,无论是横梁还是竖梁,梁上弯矩均呈对称分布,在锚固力作用点出现较大正弯矩,在跨中位置出现最大负弯矩;最大正弯矩均位于横梁和竖梁的边节点处,横梁表现的更为明显,该现象与锚固力在横梁和竖梁上的分配有关;且2种方法所得梁截面惯性矩对横梁、竖梁的弯矩均有影响,其中,对竖梁影响较大,对横梁影响较小。在竖梁的锚固力作用截面,换算截面法所得正弯矩比传统方法所得正弯矩大6.2%;在竖梁跨中截面,换算截面法所得弯矩数值比传统方法所得弯矩数值大10.1%。

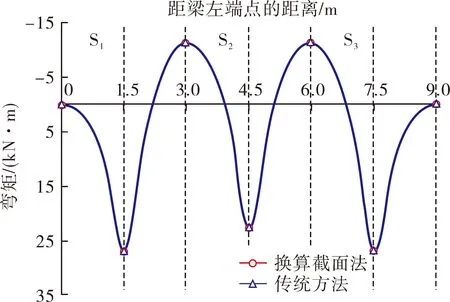
(a) 横梁H2

(b) 竖梁S2图4 框架梁弯矩对比

为研究锚固力的大小对框架梁弯矩的影响,本文以竖梁为研究对象,按照传统方法和换算截面法分别计算了锚固力为50、100、200、300、500、800 kN时关键截面的理论弯矩,结果见表2。

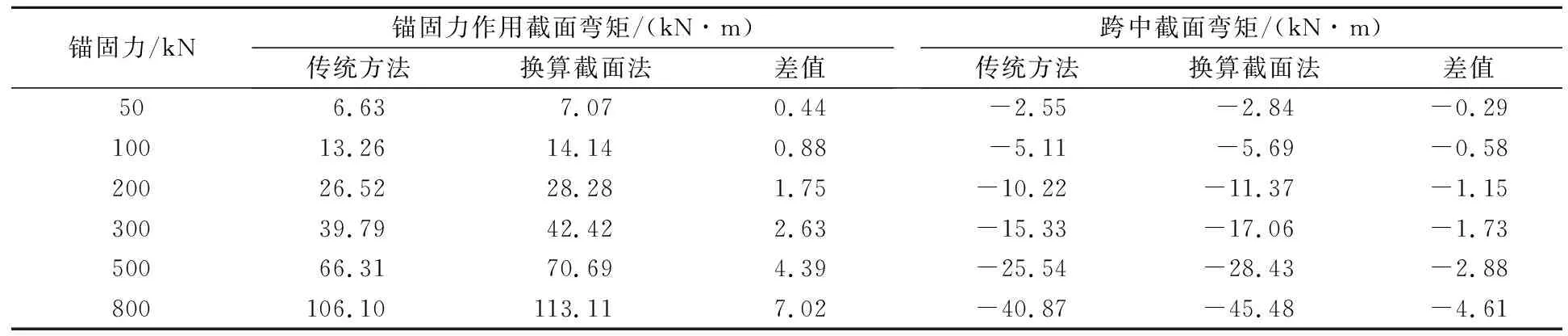
表2 不同锚固力等级下2种方法所得竖梁弯矩

结果表明,锚固力越大,梁截面的弯矩值越大,二者呈现同比例增减的变化规律。与传统方法相比,采用换算截面法可以增大框架梁关键截面的理论弯矩,提升框架梁的抗弯能力,进而在相同工况下减小框架梁的截面配筋率,对框架梁的设计具有优化作用,且锚固力越大,优化作用越明显。此外,采用换算截面法求解梁截面惯性矩考虑了框架梁材料的非单一性,更加符合工程实际。

3 现场试验

3.1 试验方案设计

在该边坡计算剖面的第二榀框架梁上选择中横梁H2和中竖梁S2的跨中及两端截面布置传感器,每个截面布置2个传感器,对称安装于该截面上下两侧受力主筋上,考虑到框架梁受力时具有一定的对称性,中横梁H2一侧远端截面不设置传感器,传感器布置见图5。

图5 第二榀框架梁传感器布置

3.2 实测弯矩值计算

在现场试验中,框架梁各截面弯矩值无法直接监测得到,可以通过所测钢筋应力、应变值反算求得。本文引入一种基坑工程推算地下连续墙实测弯矩的方法进行框架梁实测弯矩的求解[11],根据材料力学的方法,利用实测应力推算梁截面的实测弯矩值,有

(6)

式中,M为待测截面弯矩,框架梁取一延米计;Ec、Es分别为混凝土、钢筋的弹性模量;I0为待测截面的惯性矩;d为1对钢筋计之间的中心距离;σ1、σ2为1对待测钢筋计的应力值,受拉为正,受压为负。

此时,依旧采用换算截面的方法确定梁截面惯性矩,即令I0=Ic。同时,由于框架梁受力时中和轴可能发生变化,利用实测的受拉区钢筋应力σs1和受压区钢筋应力σs2确定中和轴xc的位置,令ξ=σs2/σs1,即

(7)

最终,框架梁截面实测弯矩为

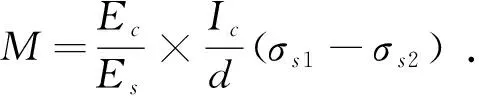
(8)

4 试验结果及对比分析

由于框架梁变形、注浆体强度及锚具等因素的影响,锚索张拉锁定后,锁定值会经历一个加速损失阶段,导致锁定值大幅减少。该试验对部分锚索的锚固力进行了现场监测,由实测数据显示,试验区域锚索锚固力的实测平均值为174 kN。

根据本文的理论计算方法及实测钢筋应力推算法,可以得到第二榀框架梁在实际工况下截面理论弯矩值和试验的实测弯矩值,与设计工况下梁截面理论弯矩值进行对比分析,对比结果见图6。

(a) 横梁H2

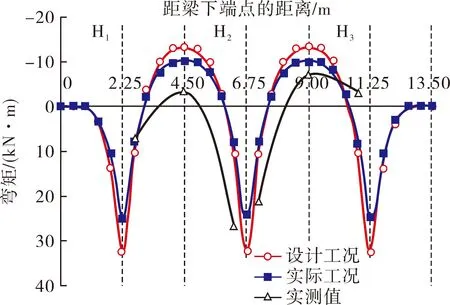
(b) 竖梁S2图6 3种工况下第二榀框架梁弯矩对比

该试验中,锚索作用点位置配筋复杂,无法布置测点,传感器布置于节点两侧截面,因此未将节点两侧的实测弯矩进行连接。由实测弯矩可以看出,框架梁节点张拉锁定后,横梁、竖梁节点位置的梁底均处于受拉状态,跨中位置的梁底均处于受压状态,锚索作用点附近存在最大正弯矩,框架梁的跨中位置出现最大负弯矩,实测弯矩值与理论弯矩值的分布趋势基本吻合,除个别测点外,其余测点的实测弯矩值均小于理论弯矩值。

究其原因,这是由于求解理论弯矩值时忽略了岩土体与梁底的水平摩阻力作用,水平摩阻力对地基梁内力及变形有较大影响;其次,锚索张拉锁定后的预应力损失也是导致实测弯矩值偏小的一个重要原因;另外,由于施工因素的影响,部分传感器的安装截面与设计存在偏差,进而导致个别测点的实测弯矩值偏大。

与设计工况相比,实际工况下横梁、竖梁关键截面的理论弯矩值均显著减小,关键截面弯矩值减小了24.35%,与锚固力损失率相同。框架梁的实测弯矩与实际工况下的计算弯矩更为接近,验证了锚固力对框架梁内力变化的重要影响。

5 结论

1) 基于Winkler弹性地基梁理论,引入“换算截面”的方法计算框架梁的截面惯性矩,给出了一种框架梁内力计算的新方法,该方法考虑了框架梁材料的非单一性,更加符合工程实际。该方法可以增大梁截面的理论弯矩,提升框架梁的抗弯能力,减小框架梁截面配筋率,且锚固力越大,这种能力越明显。

2) 结合现场试验,引入了一种采用实测应力值推算框架梁弯矩的新方法,该方法考虑了梁截面为“双筋截面”的特点,以及实际受力状态下中和轴位置的变化,与框架梁的实际工作状况更为接近,所得实测弯矩更为准确。

3) 锚索锚固力对框架梁内力的影响显著,锚固力越大,框架梁弯矩越大,且二者呈现同比例变化规律。由实际工况下理论弯矩分布可知,横梁和竖梁关键截面的弯矩值均减小了24.35%。因此,工程中应采取必要措施减小锚固力损失,避免框架梁发生破坏,进而威胁边坡安全。