基于JT-AR转换模型的非高斯风荷载特性分析

孙芳锦,阳立云,路明璟,张大明,曾 倩

(1.桂林理工大学 a.土木与建筑工程学院; b.信息科学与工程学院,广西 桂林 541004; 2.广西岩土力学与岩土工程重点实验室,广西 桂林 541004; 3.辽宁工程技术大学 土木工程学院,辽宁 阜新 123000; 4.广西嵌入式技术与智能系统重点实验室,广西 桂林 541004)

在对大跨度屋盖的研究中,大多数学者认为大跨度结构表面的风荷载分布为高斯平稳过程,对风荷载尤其是非高斯脉动风荷载作用下结构动力性能及非稳定性研究较少,这通常会低估风荷载极值,导致计算结果偏小。因此如何更快速、准确地获取大跨度结构非高斯风压时程是大跨度结构等建筑类型领域的热点问题。

王煜成[1]研发适用于大型屋盖的风荷载实测系统,按照高度合理布置测点,进而实现数据的高效采集。Fabio等[2]对双曲抛物面屋顶进行了风洞试验,总结出风荷载显著改变了结构固有振动频率和阻尼比。李正良等[3]研究复杂大跨度屋顶在24个风向下的风荷载特性,给出在抗风设计过程中,应更加注意四肢区域的建议。Li等[4]对空气支撑膜结构进行现场检测获取风致响应的数据,并与数值模拟进行对比,考虑脉动风荷载的结构位移响应的极值与实测值相对更为一致。赵强[5]通过风洞试验在频域和时域2个角度对不同工况下的球壳屋盖结构表面风荷载特性进行分析,总结出非高斯区域划分方法及空间相干性规律。尽管如此,布置此类现场实测及风洞试验的测点多且复杂,大多数位置的风压数据仍需根据少数点的实测记录进行数值模拟及预测获得。

部分学者提出利用数值模拟获取大跨度结构非高斯风压时程的方法,代替对风场全面测量和繁琐的风洞试验。双妙等[6]在Hermite矩模型基础上,根据Kaimal谱生成某典型风机结构正常运行和停机状态下,高斯、非高斯硬化和软化三种不同概率特性的风场,对风机进行全寿命可靠性分析。李锦华等[7]利用时变平均风速和调制Kaimal谱生成非平稳非高斯脉动风速,模拟脉动风速样本的相关函数具有时变特性,瞬相关函数与相应目标一致。

为了更加快速地获取非高斯风荷载,本文介绍了一种运用JT-AR转换模型模拟大跨度球面屋盖结构非高斯脉动风压的方法。该方法基于JT变换和AR模型理论进行耦合,提出并构建JT-AR转换模型,模拟生成非高斯脉动风压时程样本数据,与目标功率谱及高阶统计量对比验证;再通过已有风洞试验结果与作用在大跨度球面屋盖结构表面的非高斯分布特性进行对比分析,验证其模拟结果的可行性。

1 非高斯脉动风压模拟理论基础

在对结构风工程的非高斯特性研究中,现已研究出多种转换过程模型可将高斯过程通过转换函数转换为非高斯过程,主要是利用转换函数手段,进而使潜在高斯随机过程与目标非高斯随机过程之间进行相互转换。

1.1 Hermite转换分布

Hermite转换模型理论的核心思想是以一个单调转换函数为中介,实现潜在高斯随机过程和目标非高斯随机二者的相互转换,即

(1)

式中:y是非高斯过程;u是均值为0、方差为1的标准高斯过程;g(u)是单调转换函数;FY、Ψ(u)分别是非高斯风压时程和高斯风压时程的累计概率密度函数。

Winterstein[8]提出在目标峰值大于3时的标准非高斯过程,可以考虑利用Hermite多项式表示潜在高斯过程与目标非高斯过程的转换函数。现今早已提出过很多转换过程模型,其中Hermite转换模型最为常用。

1.2 Johnson变换

目前在非高斯风荷载研究领域,JT变换的应用较少。JT变换的适用范围覆盖到整个由偏度和峰值所构建的Pearson平面。与Hermite转换模型相比,JT变换的适用范围更广,但其劣势在于缺少准确可靠的经验公式。

1.3 线性滤波法及边缘矩关系

常用的脉动风速时程模拟方法运用最广泛的是线性滤波法,其原理是:将零均值的白噪声随机序列通过设计好的滤波器,使其输出为具有指定功率谱密度函数的平稳高斯随机时间序列。

基于前四阶边缘矩[9],本文以大跨度球形屋盖结构为工程背景,提出针对单变量的JT-AR转换模型的模拟方法,生成大量的仿真非高斯风压时程,进而模拟大跨度球面屋盖结构非高斯脉动风荷载分布特性。

2 大跨度球形屋盖结构高斯风荷载模拟

2.1 高斯风荷载模拟方案及参数设置

屋盖直径是80 m,屋檐高度为25 m,屋盖的最高点位置为35 m。设置流场平均风压为15 m/s,地面粗糙系数是0.002 5,正西方向设为风向的0°方向,逆时针为负。建立大跨度球形屋盖结构几何模型(见图1),提取典型点的坐标并导入到MATLAB中,测点布置如图2所示。

图1 大跨度球形屋盖模型

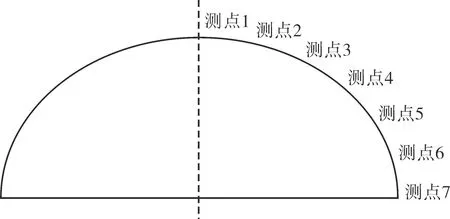
图2 测点布置

研究发现,湍流强度I(z)与地貌形式相关,湍流强度随空间升高而降低。我国相关规范给出不同地形的地面粗糙度,相关关系式为

(2)

式中:α表示地面场地粗糙度指数;I10(z)表示高度10 m处名义湍流强度,按照规范给出A,B,C,D四类,分别为0.12、0.15、0.22、0.30。

本文在AR自回归系统中设定的基本参数见表1,生成高斯白噪声序列,对于目标脉动风速谱取Davenport谱。

表1 AR自回归系统基本参数

可以通过下式将脉动风速谱转换为脉动风压谱,即

(3)

ρij=exp

(4)

式中:C的取值与地面粗糙度、离地高度及湍流度等有关,取Cx=16,Cy=8,Cz=10。

2.2 高斯风荷载模拟结论及分析

通过AR自回归系统模拟仿真生成各测点具有指定目标功率谱密度、高阶统计量等目标指标的大跨度球形屋盖结构高斯脉动风压时程,同时给出典型点在置信度0.95的累积计算函数图及评价手段,以此验证模拟结果的准确性。由于篇幅有限,本文以典型点1和典型点4为例。测点高斯风压如图3所示;测点的高斯风压时程PSD与目标PSD对比如图4所示;测点的高斯风荷载ACF图如图5所示;高阶统计量等目标指标如表2所示。

表2 模拟脉动风荷载统计量与目标统计量

(a) 1节点

(b) 4节点图3 测点高斯风压时程对比

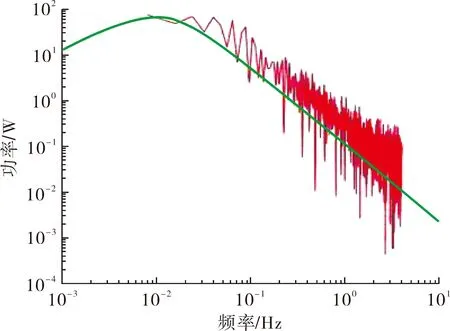
(a) 1节点

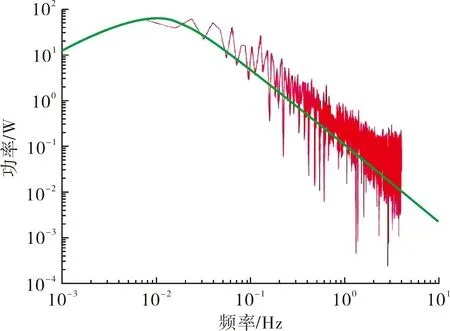
(b) 4节点图4 测点的高斯风压时程PSD与目标PSD对比

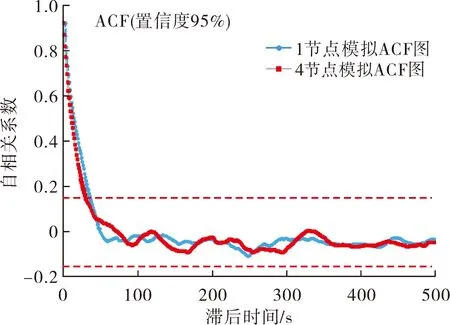
图5 测点的高斯风荷载ACF图

通过图3发现,各点的脉动风压时程具有较明显的对称性和平稳性,AR自回归系统模拟结果的高斯特性明显。由图4可知,模拟结果与目标高斯脉动风压功率谱密度函数拟合精度高,满足目标功率谱密度要求。由图5可知,自相关系数在滞后时间达到50时落入置信范围中,与功率谱密度函数发展趋势相对应,表现出良好的稳态。由表2发现,7个测点的高斯脉动风压时程的偏度系数和峰值系数都在目标值附近浮动,且接近于目标值。综上,本次对高斯脉动风荷载的模拟满足对目标非高斯脉动风压时程模拟的功率谱密度函数、偏度和峰值等试验条件和相关要求,可以进行非高斯脉动风荷载模拟。

3 非高斯脉动风荷载模拟

3.1 非高斯风荷载模拟方案及参数设置

通过Johnson变换,将AR自回归系统得到的高斯脉动风压时程转换为非高斯脉动风压时程。为与高斯风荷载模拟过程作对比,用于模拟非高斯过程的脉动风功率谱密度函数(PSD均采用Davenport谱),采样点数,空间相干函数,时间步长等参数均与高斯过程相同,但目标高阶统计矩则不同,Johnson 变换基本参数如表3所示。

表3 Johnson 变换基本参数

(5)

3.2 非高斯风荷载模拟结论及分析

低阶统计量无法准确映射目标非高斯脉动风压时程,不能对模拟结果进行准确地分析。因此引入高阶的统计量,可以弥补低阶统计量在模拟过程的缺陷,更加具体描述脉动风非高斯特性及非高斯脉动风荷载对大跨度结构的影响作用,使得模拟结果更加贴近实际结构受力情况。

绘制累积概率密度函数曲线及概率密度函数积分曲线,如图6所示。模拟大跨度球形屋盖上节点的非高斯脉动风压时程如图7所示。测点的非高斯风压时程PSD与目标PSD对比如图8所示。测点的高斯风荷载ACF图如图9所示。非高斯高阶统计量如表4所示。

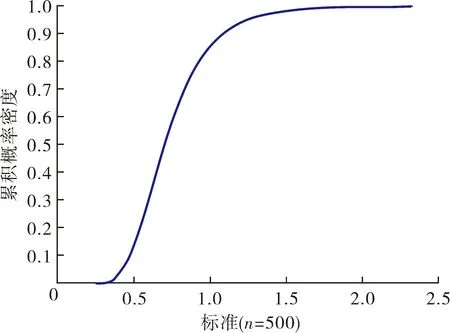
(a) 累积概率密度函数曲线

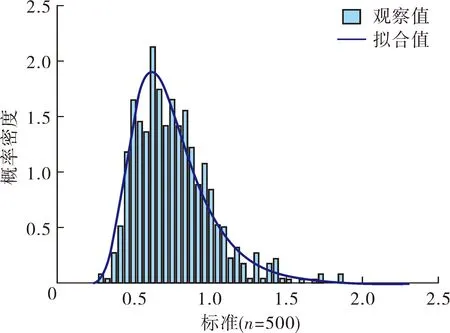
(b) 概率密度函数积分曲线图6 Johnson变换概率密度函数

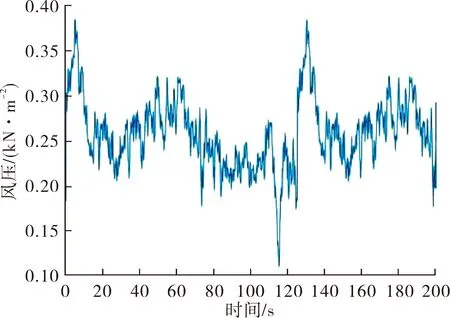
(a) 1节点

(b) 4节点图7 测点的非高斯风压时程对比

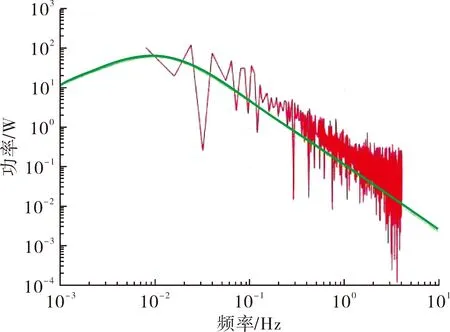
(a) 1节点

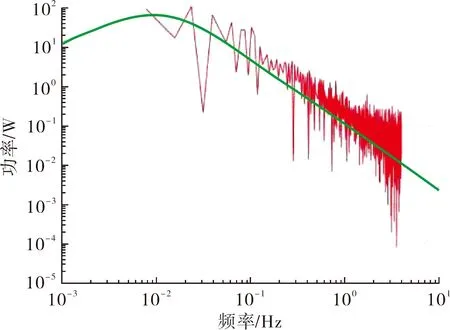
(b) 4节点图8 测点的非高斯脉动风压PSD对比

图9 测点的非高斯脉动风压变换下ACF图

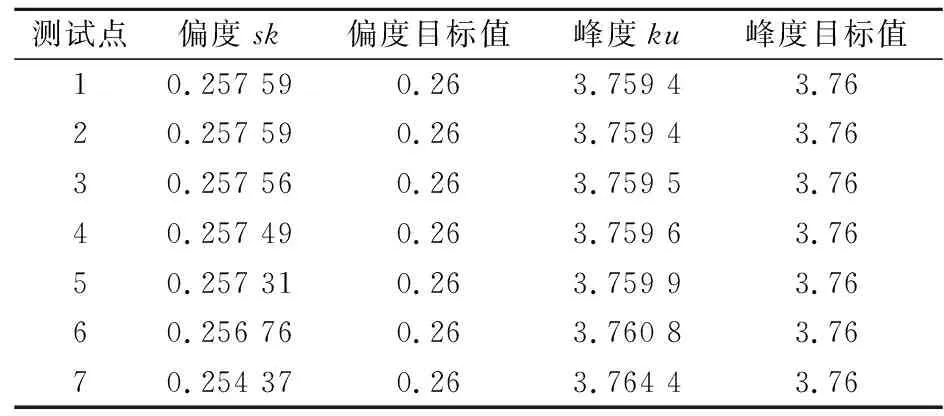
表4 非高斯脉动风荷载模拟统计量

由图6可知,Johnson变换较好地包含了概率密度和累计概率密度函数所对应的非高斯脉动风压极值。由图7可知,测点的脉动风压时程图不具备较明显对称性和平稳性,且在模拟时间段内有大幅度的风压脉冲,证明该过程具有明显的非高斯特性。由图8可知,模拟的非高斯脉动风压时程分布特性较好的吻合了目标谱,符合目标功率谱密度要求。由图9可知,测点的非高斯脉动风荷载均在50滞后时间在零值附近分布,表现出良好的稳态性。表明Johnson变换后并不影响时间序列分布。

由表4可知:各测点脉动风压时程的偏度系数、峰值系数均非常接近目标值,且两者误差不超过5%;表明试验模拟大跨度屋盖结构表面的7个典型点的脉动风压时程是非高斯脉动风压时程,都满足目标高阶统计量的要求。

4 风洞试验验证分析

4.1 非高斯脉动风建立及验证

数值模拟结果和相应的物理模型在1:100几何缩尺比例,试验结果具有较好的参考性。因此在验证非高斯风荷载和风压场模拟的正确性时,采用直径为80 m的大跨度球形屋盖结构作为目标结构,按照比例构建模型并赋予其特定的表面材料参数及变量。将JT-AR转换模型得到的非高斯脉动风压时程作为Fluent软件流场入口条件导入到大跨度球形屋盖结构表面,构建符合现实实测和风洞试验的流场环境和地形条件的计算域,监测大跨度球面屋盖结构表面典型点的非高斯脉动风压时程与原有的风洞试验结论进行对比分析。流体运动分布剖面图如图10所示;7个典型点非高斯时程如图11所示。

图10 流体运动分布剖面云图

图11 典型点非高斯风压时程

观察图10发现:大跨度球形屋盖结构的迎风面和背风面有着明显的非高斯特性区域和高斯特性区域,并且非高斯特性分布差异明显,沿屋盖高度及方向呈不均匀分布,脉动风压表现出明显非高斯特性。

基于JT-AR转换模型获得的典型点非高斯脉动风压时程(见图11),由于大跨度球形结构屋盖风场的漩涡作用,迎风面和背风面区域呈现出明显不对称性,且迎风和背风区测点非高斯风压分布均呈现明显的脉动冲击现象,脉动风压时程曲线常常伴随着很大的负向毛刺,且随高度的降低,脉冲现象逐渐明显。而其他测点,风压信号基本在风压均值附近上下波动,且波动幅度并不剧烈。但总体分布形势大致相同,满足风洞试验模拟要求。

4.2 风洞试验对比验证

赵强[5]构建非高斯脉动风场下的某个大跨度球形屋盖的风洞试验环境,对建筑结构表面风荷载特性进行研究,获得大跨度球形屋盖结构表面在非高斯风场下的风压分布特性等值线(见图12),经过与现场实测的结果作对比,佐证了风洞试验的可靠性及数据的准确性。本文将利用该风洞试验结论,在相同工况下证明所得的非高斯脉动风压分布云图的准确性。球形屋盖的风压分布特性图如图13所示。

图12 非高斯脉动风压分布特性云图

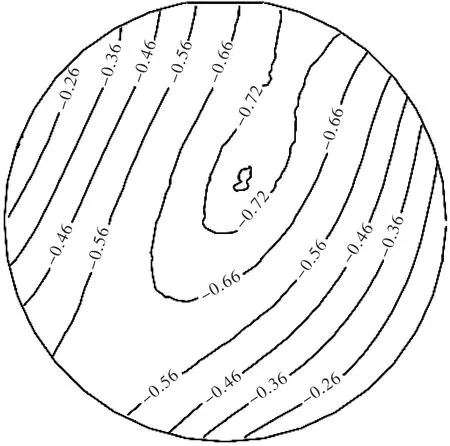
图13 球形屋盖结构风洞试验风压分布特性

对比图12和图13,在数值模拟的风压系数分布等值线图中屋盖顶部与附着点之间出现风吸力漩涡区域,平均风压大体以吸力作用为主,风吸力最大值发生在屋盖顶部,以屋脊为对称轴,测点的平均风压系数随高度的增加而增加。与模拟的平均风压系数对比,风洞试验的结果数值略高于模拟的,考虑是风洞试验的缩尺效应,且在选取典型点时采取的是无滑移壁面造成的。在后期处理过程中,可通过添加相关系数来抵消软件内部设置造成的误差。综合分析,利用JT-AR转换模型仿真非高斯脉动风压时程与风洞试验对比验证,二者非高斯风压分布特性规律及数值拟合结果基本吻合。

5 结论

1) 通过将Johnson变换与AR模型耦合,模拟生成非高斯脉动风荷载,并与目标统计量对比分析,发现模拟结果的功率谱密度函数曲线与指定功率谱密度函数曲线吻合度较高,具有明显非高斯特性;自相关系数图显示在相同频域范围内,风压分布与功率谱密度分布趋势一致,模拟高阶统计量与目标高阶统计量差距不超过5%。表明JT-AR转换模型方法模拟的非高斯脉动风荷载具有可行性及准确性。

2) 获得7个典型点的非高斯脉动风压时程与风洞试验得到的风压时程进行对比。两者误差不大且分布特性规律一致,相同时间内非高斯风压分布特性及峰值分布均一致;对比大跨度球形屋盖结构表面风压分布特性云图,发现二者分布差距不超过10%。JT-AR转换模型模拟结果与风洞试验作用在建筑上的非高斯脉动风具有同等作用影响,可为大跨度结构抗风设计计算方法提供参考。