基于Petri网的汽车涂装流程建模及可达性分析

刘芙洁,卢 可

(安徽理工大学 数学与大数据学院,安徽 淮南 232001)

随着业务流程管理水平不断提高,流程的复杂性也在增加。而Petri网作为一种对离散事件系统建模的强大工具[1-3],能够精确地描述流程中的并发、同步和冲突等关系,从而提供了对复杂流程行为的形式化表达。它还支持一个清晰的图形的可视化,以正确地观察系统。可达性作为 Petri 网的动态性质之一,在使用 Petri 网建模的系统的分析和控制中起着至关重要的作用,因为系统的活性和无死锁等性质都可以通过可达性进行分析。

可达性问题一直是Petri网理论研究的重点。它是分析Petri网结构和行为性质的基础。目前主要有可达图,状态方程和T不变量等方法来求解可达性。可达图是一种直观的方法,对于流程的动态性质,如活性和死锁等性质能进行有效表达。文献[4]将Petri网应用于再制造工艺的制定,通过可达性图生成和搜索一个最优或接近最优的可行计划。文献[5]提出了一种计算高效的方法,通过仅搜索可达性图的一部分来获取Petri网中的死标识和FBM。文献[6]开发了一种基于基础可达性图(BRG)概念的方法,这是一种用于抽象Petri网状态空间的有效工具,而无需构建整个可达性图。文献[7]采用紧凑的结构,即 minimax-BRG,研究了有界Petri网中确定原点状态的存在性,可逆性,活性和无死锁的问题。状态方程和T不变量是代数方法,具有较强的数学基础,可以很好地求解变迁向量。文献[8]通过扩展具有资源和消息因素的Petri网,给出了一种协同应急过程的系统建模和验证方法。通过可达性分析,对RMWF-Net的正确性进行了形式化定义和验证。文献[9]研究了连续Petri网及其扩展定义的有理数集,以及连续向量加法系统在可达性和决策问题方面的应用。文献[10]使用关联矩阵和状态方程来分析网系统的活性和安全性,并使用唯一可达向量网的方法来分析模型的可达性。文献[11]提出了一种基于电路的子网方法,用于在Petri网中检测无法到达的标记。通过分析具有基于无令牌电路的子网来确定状态方程是否具有非负整数解,并可以有效地处理资源不可靠的系统。

本文利用Petri网对汽车涂装生产线的具体流程进行建模,并加入了相关活动操作以此优化模型,然后,通过构造模型的关联矩阵及可达状态,对所建立的Petri网模型的可达性及安全性等相关性质进行分析验证。实现生产过程的可视化监控,从而对整个生产流程进行及时发现和调整,保证稳定生产且不断优化生产过程。

1 基本概念

Petri网是由库所(place)、变迁(transition)、托肯(token)值和连接库所与变迁并表示它们之间关系的有向弧线所组成的一种有向图。其中库所用于描述系统可能的状态;变迁用于描述修改系统状态的活动;托肯表示系统的资源;有向弧规定状态和活动之间的关系[13]。

定义1[13](变迁发生规则)PN=(P,T;F,M0)为一个Petri网,满足下列变迁发生规则。

1) 变迁t∈T具有发生权,当且仅当∀p∈·t:M(p)≥1,记作M[t>;

2) 若M[t>,从标识M发生变迁t,得到一个新的标识M′,记作M[t>M′,对∀p∈P有

定义2[13](关联矩阵)Petri网PN=(P,T;F,M0)的关联矩阵表示为A=[aij]mn,其中

aij=aij+-aij-,i∈{1,2,…,m},j∈{1,2,…,n},

定义3[12](可达性)已知Petri网PN=(P,T;F,M0),如果存在t∈T,使M[t>M′,则称M′从M直接可达。如果存在变迁序列t1,t2,…,tk和标识序列M1,M2,…,Mk,使得M[t1>M1[t2>M2…Mk-1[tk>Mk,则称Mk从M可达。从M可达的一切标识的集合记为R(M)。

定义4[12](行为轮廓)PN=(P,T;F,M0)为一个网系统,BP={→,+,||}为网的行为轮廓,表示网中所有关系的集合,对于一对变迁(t1,t2)∈(T×T)满足下列条件:

1) 若t1>t2且t2>t1,则称严格序关系,记作t1→t2;

2) 若t1>t2且t2>t1,则称排他关系,记作t1+t2;

3) 若t1>t2且t2>t1,则称交叉序关系,记作t1||t2。

2 汽车涂装流程建模

2.1 构建模型

汽车涂装工艺流程[15]是一个复杂的工业过程,涉及多个操作步骤和资源调度。涂装是指对汽车表面进行外观修饰,涂装质量的优良对于汽车的价值有直观的影响。涂装生产线主要由几个关键工序组成,包括第一道工序前处理、电泳、PVC涂装、中涂、面漆和精修等。图1给出了利用Petri网对涂装流程建立的模型。

图1 涂装流程原模型

由图1可知,从焊装车间来的汽车车身,经过预清洗(t0)进入第一道工序前处理(t1),然后执行电泳线中的活动(t2),这一部分都是按照严格序关系依次执行的;执行电泳检查活动(t3),此时存在一个排他关系,即检查不合格,需重新返回电泳(t4),检查合格,进行电泳打磨(t5)及PVC涂装活动(t6),这一部分按照严格序关系依次执行;接着执行中涂活动(t7→t8→t9),即按照严格序关系依次执行;完成中涂后,进入喷面漆工序,按照严格序关系依次执行t10→t11→t12,然后对汽车车身检查抛光(t13),若出现车身颜色不均,喷涂不平整等情况,选择执行活动t14,进行重打磨回到面漆工序,若抛光检查合格,则选择执行点修补活动(t15);按照顺序结构执行检验活动(t16),此时存在一个排他序关系(t17+t18),根据检验结果,质量问题严重程度,选择点修,即执行t17或执行t18,返回前一道工序即可,若问题严重,选择大修,即执行t19,返工回到前处理,重新进行喷涂;若检验合格,则执行喷腊活动(t20),至此喷涂流程结束。

2.2 模型优化

生产线上通过传感器、监测设备和质检仪器等手段收集数据,并与车辆信息等相关数据进行关联和记录[14]。这样可以实现全面监测、数据分析和质量追溯,从而提高工序的效率和质量。本文考虑完成涂装流程上活动所需要的活动操作来优化模型,为生产质量以及生产效率的改进提供有效的支持,优化后的模型如图2所示,其中优化的部分用虚线框出,优化后的模型可以提供更全面的信息和实时控制能力。

图2 涂装流程优化后模型

下面是对增加的活动操作说明及其行为关系:

完成前处理活动(t1),需要考虑分析表面清洁度(t2)、记录现场环境参数(t3)、记录使用清洗剂和工艺参数(t4),并且t2、t3、t4是交叉序关系,只有执行了活动t2t3t4,活动t5才会发生,即前处理活动完成。完成电泳活动(t6表示活动开始,t9表示活动完成),既要设定电泳槽参数(t7),又要记录电泳涂料质检数据(t8),变迁t7、t8处于交叉序关系。完成喷PVC活动(t13活动开始,t17活动完成),从PVC涂料配方记录、喷涂参数记录、PVC涂层质量检测数据3个方面完成喷涂活动,分别对应变迁t14、t15、t16,它们之间是交叉序关系。增加车辆信息记录(t19)、涂漆参数设定(t20)、数据采集与监控(t21)完成喷中层漆活动(t18活动开始,t22活动结束),变迁t19、t20、t21它们之间处于交叉序关系。参数设置和调整(t27)和面漆质检数据的记录(t28)需要在喷面漆活动中完成。完成检查抛光活动(t31),涉及以下3个交叉序关系的活动:收集检查数据(t32)、记录瑕疵位置和类型(t33)、记录抛光数据(t34)。

3 可达性分析

定理2[13]设PN=(P,T,F,M)为一个Petri网,A为网的关联矩阵,如果M[ti>M′则有M′=M+(Ai*)T。

选取模型中描述电泳流程的子网,记为N1。

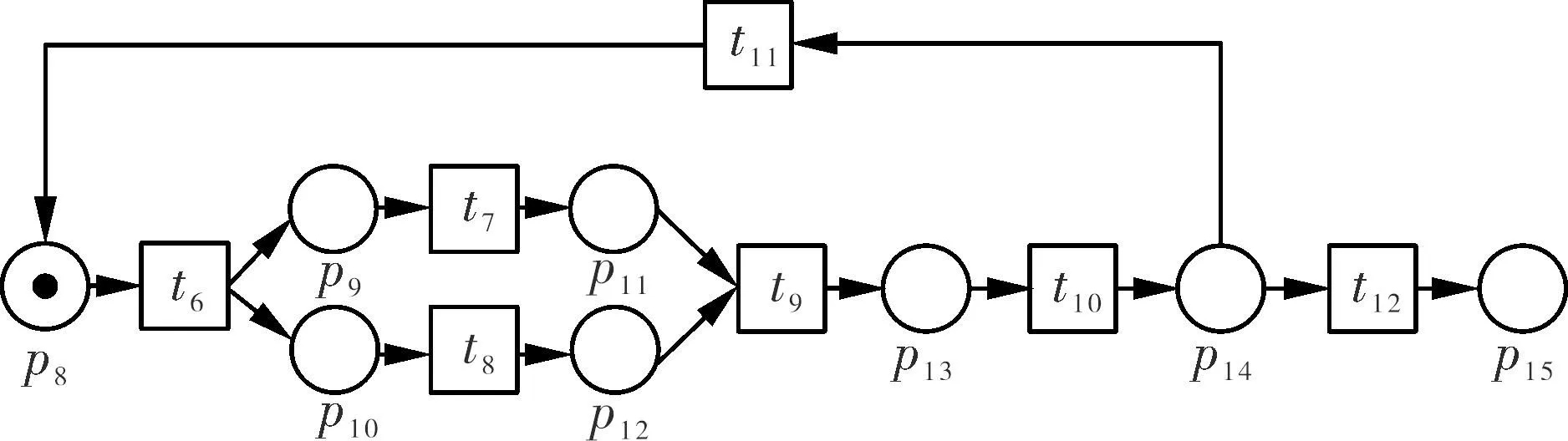
图3 子网N1

N1的输入矩阵、输出矩阵、关联矩阵分别为

M1=M0+(A1*)T

⟹[0,1,1,0,0,0,0,0]T=[1,0,0,0,0,0,0,0]T+[-1,1,1,0,0,0,0,0]T

⟹[0,1,1,0,0,0,0,0]T=[0,1,1,0,0,0,0,0]T

M1从M0可达。

同理,由定理1判断t7在M1下可以发生,产生新的标识M2=[0,0,1,1,0,0,0,0],

M2=M1+(A2*)T

⟹[0,0,1,1,0,0,0,0]T=[0,1,1,0,0,0,0,0]T+[0,-1,0,1,0,0,0,0]T

⟹[0,0,1,1,0,0,0,0]T=[0,0,1,1,0,0,0,0]T

M2从M1可达。

t8在M2下可以发生,产生新的标识M3=[0,0,0,1,1,0,0,0],

M3=M2+(A3*)T

⟹[0,0,0,1,1,0,0,0]T=[0,0,1,1,0,0,0,0]T+[0,0,-1,0,1,0,0,0]T

⟹[0,0,0,1,1,0,0,0]T=[0,0,0,1,1,0,0,0]T

M3从M2可达。

t9在M3下可以发生,产生新的标识M4=[0,0,0,0,0,1,0,0],

M4=M3+(A4*)T

⟹[0,0,0,0,0,1,0,0]T=[0,0,0,1,1,0,0,0]T+[0,0,0,-1,-1,1,0,0]T

⟹[0,0,0,0,0,1,0,0]T=[0,0,0,0,0,1,0,0]T

M4从M3可达。

t10在M4下可以发生,产生新的标识M5=[0,0,0,0,0,0,1,0],

M5=M4+(A5*)T

⟹[0,0,0,0,0,0,1,0]T=[0,0,0,0,0,1,0,0]T+[0,0,0,0,0,-1,1,0]T

⟹[0,0,0,0,0,0,1,0]T=[0,0,0,0,0,0,1,0]T

M5从M4可达。

t12在M5下可以发生,产生新的标识M6=[0,0,0,0,0,0,0,1],

M6=M5+(A6*)T

⟹[0,0,0,0,0,0,0,1]T=[0,0,0,0,0,0,1,0]T+[0,0,0,0,0,0,-1,1]T

⟹[0,0,0,0,0,0,0,1]T=[0,0,0,0,0,0,0,1]T

M6从M5可达。即库所p15获得标识,存在变迁序列σ=t6t7t8t9t10t12,使得M0[σ>M6,优化后的模型,可以达到目标状态。

利用如下代码在Matlab软件中计算Petri网的可达性。

输入:PN=(P,T;F,M0),关联矩阵,目标状态。

输出:目标状态是否可达。

verifyReachability.m

function isReachable = verifyReachability()

places = {};transitions = {};initialMarking = [];incidenceMatrix = [];targetMarking = [];

stateSpace = generateStateSpace(places,transitions,initialMarking,incidenceMatrix);

isReachable = isStateReachable(stateSpace,targetMarking);

if isReachable

disp('目标状态可达!');

else

disp('目标状态不可达!');

end

end

function stateSpace = generateStateSpace(places,transitions,initialMarking,incidenceMatrix)

stateSpace = [];

generateState([],initialMarking);

function generateState(currentMarking,marking)

stateSpace = [stateSpace;marking];

for i = 1:length(transitions)

inputPlaces = find(incidenceMatrix(i,:) <0);

outputPlaces = find(incidenceMatrix(i,:) >0);

if all(marking(inputPlaces) >= abs(incidenceMatrix(i,inputPlaces)))

newMarking = marking;

newMarking(inputPlaces) = newMarking(inputPlaces) - abs(incidenceMatrix(i,inputPlaces));

newMarking(outputPlaces) = newMarking(outputPlaces) +incidenceMatrix(i,outputPlaces);

if ～any(ismember(stateSpace,newMarking,'rows'))

generateState([currentMarking,i],newMarking);

end

end

end

end

end

function isReachable = isStateReachable(stateSpace,targetMarking)

isReachable = any(ismember(stateSpace,targetMarking,'rows'));

end

4 仿真试验

进一步,为了能够对优化后的Petri网喷涂流程模型的合理性和可行性进行评估,使用PIPE软件对模型进行仿真模拟运行。在PIPE软件中,首先绘制出模型,随后放入token在初始库所p0中,使用“State Space Analysis”函数对模型的状态进行分析,仿真试验结果见图4。研究结果表明,优化后的模型具有一定的安全性,并且有界,无死锁,这表明优化后的模型是合理可行的。

图4 PIPE仿真模拟图及状态空间分析结果

5 结语

本文对汽车涂装流程构建了Petri网模型,并利用Petri网的知识优化了原模型。通过增加执行活动所必需的活动操作,使得在出现不可避免的质量问题时或识别到不同的车身信息,可以及时排查并第一时间有效解决,或有效调节颜色转换,保障生产的持续性。其中,使用可达性定理和关联矩阵构造可达性算法,来验证Petri网模型的可达性。通过软件仿真试验,分析了Petri网的性质并验证了模型的合理性。