咸水层中CO2溶解性能预测方法优选
董利飞,董文卓,张旗,钟品志,王苗,余波,韦海宇,杨超
(1.重庆三峡学院,重庆 404120;2.三峡库区地质灾害教育部重点实验室(三峡大学),湖北宜昌 443002)
自工业革命以来,全球对化石能源不断消耗,导致大气中CO2含量急剧上升[1-2],所引发的“温室效应”等问题受到社会各界的广泛关注[3-4]。为降低温室效应造成的影响,各国均在制定CO2的减排对策[5]。目前,深部咸水层中埋存CO2是降低温室效应的有效方案之一[6-8],CO2在深部咸水层中的埋存主要包括溶解埋存、矿化埋存、气态埋存3种机制[9-10]。其中,溶解埋存占据CO2地质埋存总量的90%左右,埋存潜力最大,在进行CO2溶解埋存时,CO2在水中的溶解度是估算溶解埋存量及评价埋存潜力的关键[11]。
目前,CO2溶解度的获取方法主要有实验测定法和模型预测法。实验方法在时间和效率方面,有时无法满足实际工程的需要,因此,越来越多的学者从模型预测法开展相关研究。当前应用最为广泛的是状态方程法,DUNA 等[12]采用状态方程法建立了CO2在纯水和咸水溶液中溶解度预测模型,可有效预测CO2在纯水和NaCl 溶液中的溶解度,但将预测范围扩展到CO2-混合盐体系时,预测误差偏大。史训立[13]建立了活度-逸度型模型,可预测多盐溶液中CO2溶解度,但是模型平均误差大于5%。MAO 等[14]利用亥姆霍兹自由能模型预测了273~1 273 K、0~500 MPa 下CO2在盐溶液中的溶解度,但模型可调参数多,求解难度大。卞小强等[15]基于改进的SRK-CPA 缔合流体方程和Huron-Vidal 混合规则,建立了基于混合规则和缔合作用的热力学模型预测CO2在纯水中的溶解度。TANG 等[16]利用PR 方程预测了CO2在水中的溶解度,但是,该模型研究的压强范围限于55 MPa以下。
以上研究主要集中于CO2在纯水及单一成分溶液中溶解性能的分析,研究涉及的温度和压强范围跨度较大;同时,在计算过程中,状态方程所涉及的优化参数多,增加了实际工程中数据收集的复杂性。因此,亟需建立一种高效、精确、适应范围广的CO2溶解度预测模型,以解决实际工程中数据匮乏的问题。马尔科夫模型善于处理数据离散且波动性大的预测问题,能对随机波动性数据进行长期预测,但要求足够多的样本,才能保证模型预测精度。而灰色GM(1,1)模型对拟合数据量少、时间短、波动性不大的数据序列有极大优势,能弥补马尔科夫模型预测所需样本数量不足的问题。因此,结合灰色GM(1,1)预测模型与马尔科夫预测模型的优点,提出平均相对误差小、计算简易、温压范围广的CO2溶解性能预测模型。
1 灰色GM(1,1)模型
1.1 模型的建立
灰色GM(1,1)模型是使用比较广泛的预测模型[17-18],该模型的建模过程是将原始的离散非负数据列进行累加,生成较有规律的新离散数据列,通过建立微分方程得到在离散点处的解,最后将计算值进行累减后即可得到原始数据的预测值[19]。具体建模步骤如下。
设最原始数据列为:
式中:X(0)为原始数据;x(0)(k)>0,k=1,2,…,n。
对X(0)进行一次累加得到新序列:

以序列X(1)为基础建立灰色模型的白化微分方程:
式中:α为发展系数;μ为灰色作用量;t为时间,单位s。
灰色GM(1,1)模型微分方程为:
为求参数α,μ的解,构建矩阵Y和B:
式中:T为转置符号。
将所得参数值代入式(4)得模型的时间离散响应方程为:
将式(7)计算值累减即可求得模型预测值为:
1.2 马尔科夫优化
马尔科夫模型是通过状态向其他状态转移的概率来预测事物的发展[20],马尔科夫模型可表示为:
式中:X(t)为初始状态概率向量,X(n)为经过(n-t)个时刻后的状态概率向量,P为一步状态转移概率矩阵[21]。
马尔科夫模型优化步骤为:将预测结果进行状态划分并确定转移概率,最后对其应用马尔科夫模型进行优化[22-23]。
1)状态划分
计算灰色模型预测值与实测值的相对误差:
式中:ε(k)为相对误差;k=1,2,…,n。
将相对误差大小进行排序并划分为若干个不同的状态区间,记为:Qk=[Q1k,Q2k],k=1,2,…,n。
2)计算状态转移概率矩阵P,计算公式为:
式中:Pkj为从k出发经过有限步首次到达j的概率;mkj为Qk转移到状态Qj的步数;mk为状态Qk出现的频数。
得到状态转移概率矩阵:
3)对预测值进行修正
设待预测值为y,以最大概率所处状态作为未来发展趋势,而预测值在区间[Q1k,Q2k]内变动,用区间平均值作为未来时刻的预测值y[24-25]。即:
式(14)中当预测值高于实际值时取“+”,当预测值低于实测值时取“-”。
2 案例分析
2.1 单一影响因素下的案例分析
2.1.1 案例一
收集CO2在水中的溶解度实验数据[26],以温度为313.15 K,压强分别为10、20、30、40、50、60、70、80、90、100 MPa 下CO2在水中的溶解度作为原始数据列:X(0)={1.237 8,1.404 1,1.485 2,1.593 2,1.706 5,1.772 1,1.870 5,1.955 9,2.058 2,2.129 6}。
选取10~80 MPa 下CO2溶解度数据进行灰色GM(1,1)建模,根据灰色GM(1,1)模型预测原理得模型参数α=-0.054 977,μ=1.312 3,将参数代入式(9)可得到模型预测公式:
根据相对误差ε(k)大小划分马尔科夫模型的状态区间,各状态区间范围分别为状态一[-1.06%,-0.06%)、状态二[-0.06%,0.94%)、状态三[0.94%,1.94%],结果见表1。
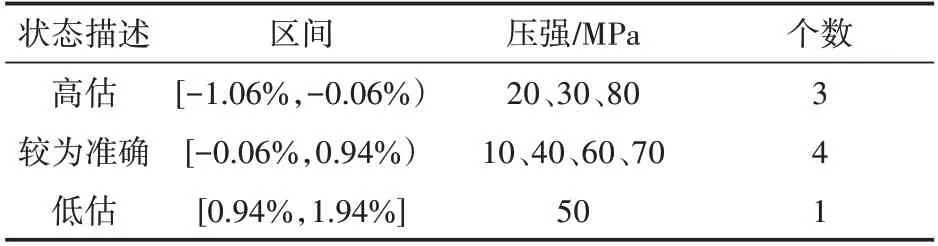
表1 模型状态区间划分Table 1 Model state interval division
应用灰色马尔科夫模型预测温度为313.15 K、压强为90、100 MPa时CO2在水中的溶解度,2种模型的预测结果见表2。

表2 灰色GM(1,1)模型与灰色马尔科夫模型预测结果对比Table 2 Comparison of prediction results between grey GM(1,1)model and grey Markov model
由表2可知,灰色GM(1,1)模型与灰色马尔科夫模型的预测值与实测值的平均相对误差分别为2.37%、1.52%,经过修正的灰色马尔科夫模型预测值相对误差降低了0.85%,预测精度高于灰色GM(1,1)模型。
2.1.2 案例二
收集CO2在水中的溶解度实验数据[26],以压强100 MPa、温度分别为313.15、333.15、353.15、363.15、373.15、393.15、413.15、433.15、453.15、473.15 K 下CO2在水中的溶解度作为原始数据列:X(0)={2.129 6,2.025 6,2.033 5,2.066 1,2.090 6,2.257 5,2.462 6,2.859 8,3.332 3,4.039 9}。同理,选取313.15~433.15 K下CO2溶解度数据进行建模,按照案例一建模流程,根据相对误差ε(k)大小将马尔科夫模型划分为4个状态区间:状态一[-7.075%,-3.455%)、状态二[-3.455%,0.165%)、状态三[0.165%,3.785%)、状态四[3.785%,7.405%)。构造状态转移概率矩阵,预测100 MPa 下温度分别为453.15、473.15 K 时CO2在水中的溶解度,2种模型预测结果见表3。

表3 灰色GM(1,1)模型与灰色马尔科夫模型预测结果对比Table 3 Comparison of prediction results between grey GM(1,1)model and grey Markov model
由表3 可知,在压强100 MPa 的条件下、灰色马尔科夫模型与灰色GM(1,1)模型预测结果的平均相对误差分别为19.29%、17.73%。相比灰色GM(1,1)模型,灰色马尔科夫模型预测值与实测值的平均相对误差减少了1.56%,预测精度提高,但2 种模型预测值与实测值之间误差明显较大,预测精度均低于实测值,这是因为高温高压下,一部分水溶剂转化为气态,造成水蒸气体积增加,使CO2在水中的溶解度偏大。因此,在高温条件下进行CO2溶解度估算时应考虑水气体积的影响。
2.1.3 案例三
据CO2在水中的溶解度测定结果[27],以温度333.15 K、压强10 MPa、矿化度分别为0、1、2、3 mol/kg时CO2在水中的溶解度作为案例三的原始数据列:X(0)={1.062,0.835,0.696,0.601}。同上,选取矿化度为0、1、2 mol/kg 时的CO2溶解度数据进行建模,预测矿化度为3 mol/kg时CO2在水中的溶解度。
计算得:灰色GM(1,1)模型预测值为0.579 mol/kg,模型预测值与实测值的相对误差为3.62%,灰色马尔科夫模型预测值为0.602 mol/kg,相对误差为0.21%,其中马尔科夫模型状态划分区间为:状态一[0,0.083%)、状态二[0.083%,0.167%)、状态三[0.167%,0.25%)。
由以上计算结果可知,与灰色GM(1,1)模型的预测结果相比,灰色马尔科夫模型相对误差降低了3.41 %,虽然2 种模型都能有效预测不同矿化度下CO2在水中的溶解度,但灰色马尔科夫模型的预测精度明显高于灰色GM(1,1)模型。
2.2 多因素影响下的案例分析
为进一步验证灰色马尔科夫模型精确性,收集不同温度、压强及矿化度条件下CO2溶解度实验数据[27](表4),应用2 种模型分别预测矿化度为0、1、2、3 mol/kg 时,CO2在压强、温度为23 MPa、343.15 K 和26 MPa、353.15 K条件下的水中溶解度。
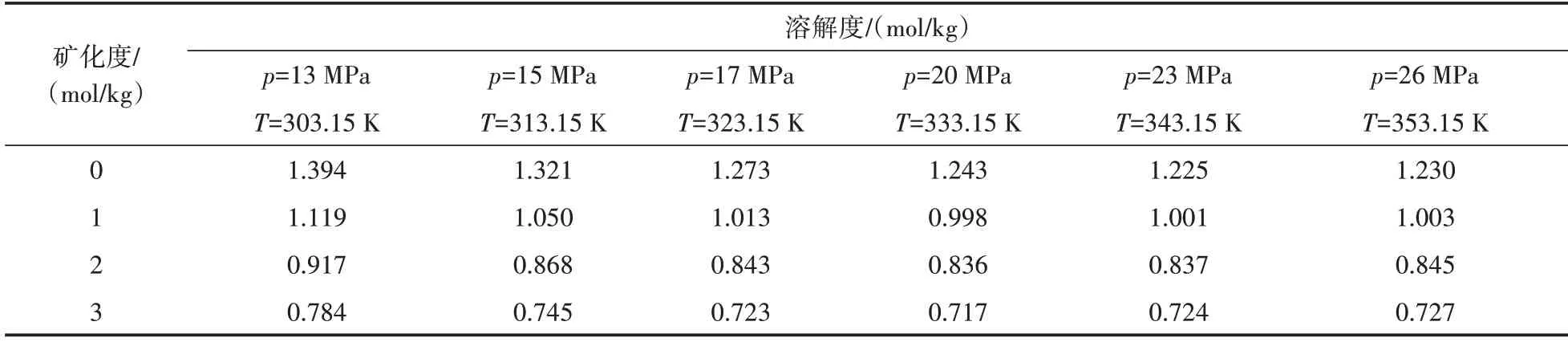
表4 不同温度、压强及矿化度下CO2在水中的溶解度Table 4 CO2 solubility in water under different temperature,pressure and salinity
根据灰色GM(1,1)模型预测值与实验值的相对误差划分状态转移概率矩阵,结合式(14),利用灰色马尔科夫模型对CO2在水中的溶解度预测值进行修正。
将2种模型的预测值与实验值进行对比,对比结果见图1、表5。

图1 2种模型对CO2在不同温度、压强、矿化度下水中溶解度的预测值与实验值对比Fig.1 Comparison of predicted values from two models with experimental values for solubility of CO2in water under different temperatures,pressures and salinity levels

表5 2种模型预测结果对比Table 5 Comparison of prediction results between two models
由图1 可知,在矿化度0、1、2、3 mol/kg,压强为13~20 MPa、温度303.15~333.15 K时,2种模型预测值与实测值拟合度较高,当温度为333.15~353.15 K、压强为20~26 MPa 时,2 种模型预测精度明显降低,结合表5发现,灰色GM(1,1)模型预测值与实验值的相对误差最高为5.81%、最低为1.82%,而灰色马尔科夫模型预测值与实测值的相对误差最高为5.58%、最低为1.47%。其平均相对误差仅比灰色GM(1,1)模型高0.03%。
3 结论
1)基于灰色马尔科夫理论,结合灰色GM(1,1)预测模型与马尔科夫预测模型的优点,提出了平均相对误差小、计算简易,温度、压强范围广的CO2溶解性能预测模型。
2)对比灰色GM(1,1)预测模型与灰色马尔科夫预测模型,在压强100 MPa、温度313.15~433.15 K范围内,2 种模型预测结果的平均相对误差分别为4.10%,0.94%,灰色马尔科夫模型预测精度优于灰色GM(1,1)模型,但当温度高于453.15 K时,2种模型预测值与实测值偏差较大,需考虑高温高压下水汽体积对CO2溶解性能的影响。
3)应用灰色马尔科夫模型对不同温度、压强、矿化度条件下CO2在水中的溶解度进行预测,平均相对误差仅为3.97%,说明该模型在预测不同温压及矿化度下CO2在水中的溶解度具有较高的精度,可为CO2在地层水中的溶解度提供一种新的预测方法。
4)提出的新型预测模型,具有数据需求少,预测精度高的优点,能满足实际工程中对CO2溶解度数据的需求,对研究CO2在咸水中的溶解度变化规律有一定指导意义。

