山地城市互通式立体交叉同侧相邻匝道最小净距计算研究

杨进, 龚华凤,2, 赵聪霄,2

(1.林同棪国际工程咨询(中国)有限公司, 重庆 401121; 2.重庆市山地城市可持续交通工程技术研究中心, 重庆 401121)

互通式立交作为城市交通系统中的重要交通节点,起着车流转换和道路之间连接的作用。随着道路里程和路网密度的增加及立交建设的复杂化,立交主线出现连续匝道出入口的情况越来越多。

相比于平原城市,山地城市地形高低起伏,道路纵坡大,除高速路与快速路外,在城市主、次干道上存在大量互通立交。该类互通立交的主线设计速度偏低,交通流量大,立交功能多样,为满足转换需求,相邻匝道间易形成短距离的连续汇入、汇出。作为山地城市路网规划和立交布局的重要研究内容,连续合、分流点净距直接影响立交的选型、规模、投资等,也影响互通式立交车辆运行状态。匝道连续分流点净距过大,则无法满足交通转换需求;匝道连续分流点净距过小,则会影响互通立交的通行能力和交通安全水平。

1 研究现状

美国等西方国家对互通式立交匝道间距与交织段的研究较早且成果较多,但因交通系统的复杂性,无法达成统一认知。1950年发布的《公路通行能力手册》(HCM 1950)基于多个州的实测数据,首次提出了针对公路交织区运行与设计的分析方法[1]。1965年发布的HCM 1965根据Normann O. K.、Karl Moskowitz等的研究成果,进一步区分了不同服务水平下进出匝道与主线的交织分析,扩大了交织段长度与交织流量的选择设计范围,但未明确交织段和上下游服务水平的影响[2]。Denney R. W.等考虑不同交织构型对交织段的影响,将交织段进一步分为主线交织和匝道交织,认为交织车辆与非交织车辆在同一服务水平下的运行速度不同[3]。文献[4]对交织区通行能力进行修改并形成了新的计算方法,但由于计算过程烦琐,该方法未得到广泛应用。1985年发布的HCM 1985对匝道端部通行能力分析方法进行修订,并考虑了匝道变速车道长度对主线外侧两条车道交通流分布的影响[5]。2010年发布的HCM 2010对交织长度、宽度和构型等进行了全新定义,同时更新了交织区通行能力计算方法[6], 但计算仅针对高速公路环境,计算中无法考虑低速下交织段通行能力。Leisch J. E.等根据大量实测交通数据,通过统计学方法和数理学方法,得出了不同交织构型情况下服务水平、交织流量、交织密度及高峰小时系数等与车道数之间的关系[7],该方法被纳入美国加利福尼亚州《公路设计手册》(HDM)[8]并沿用至今。

国内目前对互通立交净距的研究成果和设计标准多基于公路项目。贺玉龙等从驾驶员心理特征入手,建立了城市快速路互通立交最小间距计算模型[9],但预测结果基于最不利驾驶情况且假设较保守,导致预测间距过大。吴明先等分析了八车道高速公路小间距互通式立交间车辆的运行特性和变道行为,构建了最小净距计算模型,并运用数理方法结合调查数据标定了八车道高速公路小间距互通式立交最小净距模型的关键参数[10]。孙剑等对上海市60处快速路典型交织区进行调查,通过分析典型因素与交织区通行能力之间的关系,提出了城市快速路交织区通行能力模型[11]。徐俊军通过交通仿真软件模拟快速路出入口的交通运行状况,以主路车道数、主路流量、出入口交织比等影响快速路出入口间距的因素作为外部条件,对不同建设条件下快速路出入口最小间距进行了细化,预测结果与实际结果拟合较好[12]。

现行设计标准、规范对匝道净距的概念及范围尚未形成统一,导致不同标准、规范的要求差异较大。JTG/T D21—2014《公路立体交叉设计细则》中,相邻互通立交最小净距根据主线设计速度和主线车道数确定,但未提供建议值的计算过程[13];CJJ 129—2009《城市快速路设计规程》对快速路上相邻出入口间距(端部之间的距离)最小值的规定见表1[14];CJJ 152—2010《城市道路交叉口设计规程》根据不同相邻匝道组合形式(见图1)提出了相邻匝道出入口净距的一般值和极限值(见表2)[15]。

表1 CJJ 129—2009中相邻出入口的最小间距L

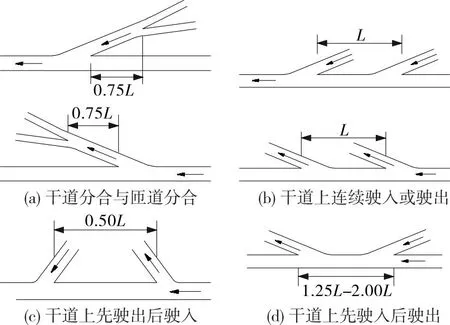
图1 相邻匝道组合形式

1.1 最小净距的定义

最初对相邻匝道距离L的界定源于美国的一系列研究成果。早期统一称为匝道距离,后期逐渐对匝道细部进行了明确。AASHTO绿皮书(2004版)将相邻匝道距离定义为相邻匝道鼻端而非物理楔形端点之间的距离[16]。得克萨斯州《道路设计手册》中建议值也指鼻端之间的距离[17]。

《公路立体交叉设计细则》定义立交相邻匝道净距为相邻入、出口之间主线基本路段的最小长度,包括变速车道渐变段,但不包括变速车道长度。《城市快速路设计规程》明确相邻出入口端部之间的距离为匝道间距,包含加减速车道长度。《城市道路交叉口设计规程》中未明确相邻匝道净距定义,但指出匝道出入口之间的间距应考虑变速车道长度,即净距不包含加减速车道长度。

综上,将匝道最小净距定义为相邻入、出口之间主线基本路段的最小长度(见图2)。

图2 相邻立交匝道最小净距示意图

1.2 交织段长度的定义

根据Leisch J. E.的研究成果和HCM 2000,交织段长度指交织区入口处三角端宽度0.6 m 位置到出口处三角端宽度3.7 m 处的距离。后期研究中对交织段长度的定义出现争议,HCM和美国得克萨斯州《道路设计手册》[17]中共包含3种长度:1) 最短交织段长度LS,指相邻入、出口之间主线基本路段的最小长度;2) 基本交织段长度LB,指相邻匝道物理楔形端点之间的距离;3) 最长交织段长度LL,指相邻匝道鼻端之间的距离。3种交织段长度见图3。美国加利福尼亚州《公路设计手册》(HDM)将交织段长度定义为相邻匝道物理楔形端点之间的距离[8]。

图3 不同交织段长度定义示意图

国内研究普遍认为交织段长度=减速车道长度+加速车道长度+渐变段长度×2+辅助车道长度[18-19]。

综上,基于交织段为车辆完成车道变换提供空间的作用,经过对比国内外标准、规范的要求及相关研究成果,将同侧先驶入、后驶出匝道之间合理的交织段长度定义为相邻匝道净距+渐变段长度×2,即相邻匝道物理楔形端点之间的距离(LB)。

2 匝道净距计算模型

HDM中使用Leisch法,通过图表的形式考虑匝道构型(同侧或双侧)和车道数配置(平衡或不平衡)进行交织段参数选择,不同服务水平下可通过交织段流量确定交织长度建议值,具体关系见图4。

1英尺≈ 0.305 m

2.1 确定服务水平

美国标准评价方法中将连续流条件下道路服务水平分为A～F 6个等级,CJJ 152—2010《城市道路交叉口设计规程》将道路服务水平分为一、二、三、四 4个等级,其对应关系见表 3。考虑到城市立交多为B类(一般立交),对立交主线与一般服务水平的匝道均建议采用Ⅱ2级服务水平(相当于美国标准中D级)下相关折减系数,针对D级服务水平(LOS D)计算对应交织段长度。

表3 中美标准、规范中立交服务水平的对应关系

2.2 确定交织段流量

HCM中将需要进行变换车道的交通量视为交织交通量。当车辆由匝道进入主路或离开主路进入匝道时,均需要进行车道变换。因此,可假设最大交织流量产生于所有入口匝道车辆都将汇入主线且出口匝道达到最大流量时。最大交织段流量为进匝道最大流量VRM和出匝道最大流量VMR之和。

按照不同匝道的交织构型(匝道车道数配置),匝道最大通行量可根据匝道基本路段通行能力C在不同立交服务水平下的比例αR进行折减。同时交织段因匝道和主线车辆有交织冲突,还应考虑主线在相对应服务水平下的折减αM。综上,交织段流量计算公式为:

式中:N=进匝道车道数+出匝道车道数

匝道通行能力见表 4,Ⅱ2级服务水平下折减比例见表 5。

表4 匝道基本路段的设计通行能力

表5 Ⅱ2级服务水平下最大通行量折减比例V/C(CJJ 152—2010)

先根据D级服务水平下不同主线和匝道构型的最大交通量,计算得到预测交织流量Vw,然后根据HDM设计曲线得到交织段长度,最后根据CJJ 129—2010要求确定相邻匝道入、出口两端的渐变段长度,从而得到净距长度计算值。

3 同侧相邻入、出口匝道最小净距建议值比较

将HDM相邻匝道最小净距与JTG/T D21—2014、CJJ 129—2009、CJJ 152—2010及英国设计标准DMRB[20]、国内相关研究成果[12]中相邻入口、出口匝道形式下最小净距建议值进行比较。为了便于在同一维度进行比较,根据工程项目建设经验,对标准中建议值做如下假设:1) JTG/T D21—2014对不同匝道速度和匝道数未作要求,但最小净距随着主线车道数的增加而增加,根据一般山地城市主线车道数,采用主线单向三车道情况下的净距建议值。2) CJJ 152—2010规定在先驶入、后驶出的情况下最小净距L所乘系数为1.25L～2.00L,根据不同匝道速度对系数进行选择,假设60 km/h时采用2.00L、50 km/h时采用1.75L、40 km/h时采用1.50L、30 km/h时采用1.25L。3) CJJ 129—2009假设出入口最小净距=最小间距-两侧匝道加减速过渡段长度。根据以上计算和假设,结合净距与交织段的关系,对不同标准、规范及相关研究中最小净距建议值进行比较,结果见表 6、图5。

表6 不同标准、规范及相关研究中最小净距建议值比较

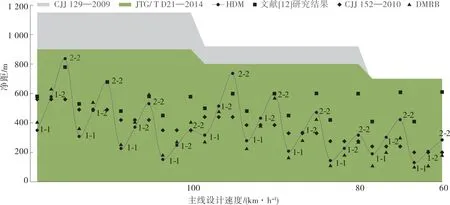
图5 不同标准、规范与研究成果中最小净距比较

从表 6、图5可以看出:1) 在30种不同工况(不同入-出匝道车道数)下,CJJ 129—2009的最小净距长度建议值均高于推荐值,平均偏差为61%。CJJ 129—2009未考虑不同匝道组合情况下交织流量对最小净距的影响,其建议值仅与主线速度相关且最小净距过长,在城市立交环境中可能较难实施。2) JTG/T D21—2014的最小净距建议值均高于推荐值,平均偏差为55%。JTG/T D21—2014仅考虑不同主线车道数对交织段长度的影响,忽略了交织段长度即交织流量与匝道通行能力的直接关系,考虑到公路对速度和密度的要求更高,JTG/T D21—2014最小净距建议值不适用于集约型城市立交。3) CJJ 152—2010的最小净距建议值中50%大于推荐值,平均偏差为30%。这是由于CJJ 152—2010建议值仅考虑交织流量低(匝道≤二进一出)情况下的最小距离,双进双出情况则通过增加辅助车道另行设计。此外,CJJ 152—2010建议值是基于驾驶员辨认标志所需时间5～10 s确定的最小距离,未考虑车辆在交织段中的运行特征,在流量较大的情况下其取值偏小。4) 英国设计标准DMRB的最小净距建议值中10%大于推荐值,平均偏差为25%。DMRB采用与HDM类似的系统,在不同主线密度和设计速度下考虑交织流量对最小净距的影响。5) 文献[12]的最小净距建议值中53%大于推荐值,平均偏差为38%。文献[12]通过建立VISSIM仿真模型,考虑交织过程中车辆组成、主线交通量、运行速度和优先通行权等因素的影响确定城市快速路出入口间距,由于模型中交通量和V/C比选择范围有限,未能给出交织流量较大情况下的最小净距。

4 结论

本文针对中国规范对城市立交相邻匝道净距定义不明确、设置不合理的问题,通过对比国内外研究体系明确最小净距和交织段的定义和构成,并基于美国加利福尼亚州《公路设计手册》(HDM),考虑主线速度、匝道速度、车道数、组合形式、服务水平等因素,计算同侧先入后出相邻匝道间的最小交织长度推荐值。将该推荐值与JTG/T D21—2014、CJJ 129—2009、CJJ 152—2010及英国设计标准DMRB、文献[12]中净距建议值进行对比,推荐值介于上限值(JTG/T D21—2014与CJJ 129—2009)和下限值(CJJ 152—2010和文献[12])之间,与 DMRB建议值的拟合度较高。

山地城市存在立交多、立交形式复杂且交通流量大等特点。根据工程项目建设经验,山地立交相邻匝道净距如直接采用JTG/T D21—2014与CJJ 129—2009建议值则过于保守,而直接采用CJJ 152—2010建议值会导致净距过小。HDM模型经过美国加利福尼亚州多个山地城市立交实践证明其取值合理,同时该模型采用图表查阅,简单直观,适用于山地城市新建、改建立交匝道的设计与评价。