艰险山区高速公路交通事故特征及严重程度影响因素分析*

张诗, 彭利飞 , 黄杰 , 王芳菲 , 徐进,4

(1.重庆交通大学 交通运输学院, 重庆 400074;2.重庆高速巫云开建设有限公司, 重庆 404546;3.重庆高速公路集团有限公司 南方营运分公司, 重庆 401300;4.山区复杂道路环境“人-车-路”协同与安全重庆市重点实验室, 重庆 400074)

交通事故已严重威胁道路使用者的生命财产安全,每年约有135万人死于道路交通事故[1]。受特殊地形地貌和自然环境等限制,山区高速公路具有线形组合复杂、桥隧比高和路侧危险度大等特点,导致其交通事故呈现数量多且程度重的现象,重、特大交通事故时有发生[2]。分析艰险山区高速公路交通事故分布特征,用定量方法揭示交通事故严重程度与影响因素之间的关系,并提出针对性的改善措施,是提高艰险山区高速公路交通安全性的有效途径。

很多学者对山区高速公路交通事故特征和致因进行了研究。Ahmed M. M.等采用贝叶斯逻辑回归方法,分析了几何线形、天气条件和车辆速度对山区高速公路交通事故的影响[3];Rusli E. R.等对比分析了山区高速公路和平原区高速公路的事故类型、严重程度、道路特征和行驶环境等的分布特征[4];Ma X. X.等建立山区高速公路事故率模型,分析了事故率影响因素[5];田毕江等基于事故数据,定量分析了云南山区高速公路交通事故的时空分布特征[6];熊晓夏等基于自然驾驶数据,建立了研究道路交通事故风险类型的贝叶斯网络模型[7];由冰玉等分别从人、车、路方面进行分析,构建了基于故障树的山区高速公路交通事故致因贝叶斯网络模型,得出了最敏感的山区高速公路交通事故影响因素[8];陈波等利用Ologit模型对山区高速公路交通事故中涉及车辆数的影响因素进行分析,得到了人、车、路环境等自变量的分类优势比[9];孟祥海等以年平均日交通量、路段长度和路段几何线形为变量,建立了山区高速公路事故率Tobit回归模型[10]。

在事故多发段和安全改善措施方面,Bolla M. E.等开发可以提供道路全面信息的交通事故数据库,确定了事故多发路段[11];Yakar F.使用相对频率法建立事故次数与道路环境的关系,对事故易发路段进行了识别[12];Guerrero-Barbosa T. E.等利用贝叶斯技术创建交通事故数据库,用于识别不同危险等级的路段[13];Sayed T.等采用模糊模式识别技术评估驾驶员、车辆、道路环境三者之间的复杂作用,识别事故易发位置[14];朱芳琪等建立基于地理信息系统的高速公路交通事故时空分析系统,结合改进时空密度聚类方法对交通事故进行了时空可视化分析和多发路段识别[15];肖乐基于NAIS国家车辆事故深度调查体系中交叉口事故数据样本,构建了以人、车、路和环境等事故严重程度影响因素的有序Logistic模型,得出显著影响因素有车辆类型、事故发生时段、是否有信号灯、驾驶员主要过失[16];杨永红等综合应用运行速度协调性分析和累计频率曲线法,确定了山区高速公路事故多发路段[17];王迎等提出了基于FCM聚类的包括人、车、路、环境的山区高速公路事故多发点成因分析方法[18];何斌等采用风险指标评价方法,从平面设计、纵断面设计及长大下坡路段等方面对山区高速公路安全性进行了评价[19]。

现有研究对一般高速公路交通事故特征分析较多,缺乏对山区高速公路交通事故发生频数和事故严重程度的特征分析;对山区高速公路交通事故分布特征的研究大都采用单因素分析方法,未进行多因素影响下事故分布特征分析;对事故严重程度影响因素的分析忽略了多因素作用下的差异性,缺少各种因素与事故严重程度的内在关系分析。为此,本文以位于重庆市的包茂(包头—茂名)高速公路南环立交至大观互通段为研究对象,通过分析交通事故在时间、空间、形态、道路线形条件及伤亡人数方面的分布特征,构建树增强朴素贝叶斯网络模型对事故严重程度影响因素进行敏感性分析,为提升艰险山区高速公路交通安全性提供借鉴。

1 研究对象及交通运行总体特征

包茂高速公路南环立交至大观互通段全长约43 km,设计速度80 km/h,最高限速120 km/h,包含8个互通立交和6条长度占路段总长22.64%的隧道,桥隧比高达75.2%,组成结构复杂,存在大量小半径曲线路段、陡坡和长下坡路段,最小圆曲线半径为700 m,最大上坡坡度、最大下坡坡度为4.0%,坡度为4.0%的陡坡路段占路段总长的10.10%,具有明显的艰险山区高速公路特点(见图1)。

选取2016—2020年该路段发生的部分交通事故数据进行研究,数据记录形式见表1。

2 交通事故分布特征分析

2.1 事故时间分布特征

从年、月、小时3个时间维度分析交通事故的频数和严重程度,结果见图2。

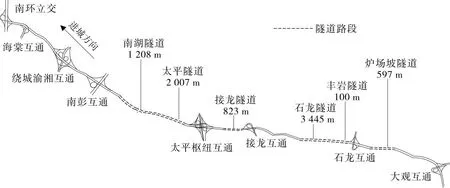
图1 包茂高速公路南环立交至大观互通段路线平面示意图

表1 2016—2020年包茂高速公路南环立交至大观互通段部分交通事故数据

从图2可以看出:1) 2017—2019年,交通事故频数呈现逐年递增的趋势;2020年,由于车流量受到新型冠状病毒感染疫情管制的影响呈不规则分布,交通事故频数急剧增长[20]。2) 2017年事故导致的伤亡人数最多,单起事故的伤亡人数最高达0.31人/起;2018年和2019年事故死亡人数最多;2020年事故伤亡人数最少。3) 1月、2月、8月、10月为事故高发月份,其中1月、2月气温较低,路面湿滑,加上春节假期,出现事故多、伤亡人数多的现象;8月受高温天气的影响,驾驶员行车舒适度降低,易引发交通事故;10月重庆处于汛期,雨雾天气多,团雾现象较明显,且该路段连接金佛山等著名景点,交通事故发生率增大,事故受伤人数最多。4) 交通事故高峰小时为9:00—11:00和13:00—18:00,这两个时段受进城和出城需求的影响,交通量激增导致事故频数较高;13:00—15:00驾驶员午后疲劳犯困,心情烦躁,极易引发交通事故;夜间1:00—7:00交通事故较少但伤亡人数较多,主要受光线和驾驶员疲劳驾驶等因素的影响。

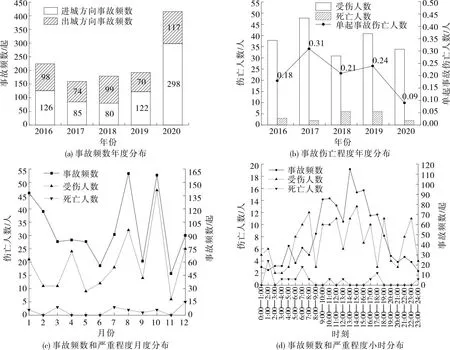
图2 事故频数和严重程度时间分布特征

2.2 事故空间分布特征

路段交通事故频数和严重程度的空间分布特征分别见图3、图4。由图3、图4可知:1) 事故多发路段集中于互通段、隧道段、陡坡段、S形曲线段和长大纵坡,其中K1613—K1621路段为长度约8 km的连续纵坡,坡度为4.0%的区段占19.80%;K1622—K1630路段为长度约8 km的连续纵坡。2) 进城方向的伤亡人数多于出城方向,伤亡人数最多的区段为K1588—K1589、K1594—K1595和K1616—K1617路段,平均15人;事故多发路段货车占比较高,货车在连续纵坡路段连续制动易导致刹车失灵或减弱,一旦发生交通事故伤亡人数较多。

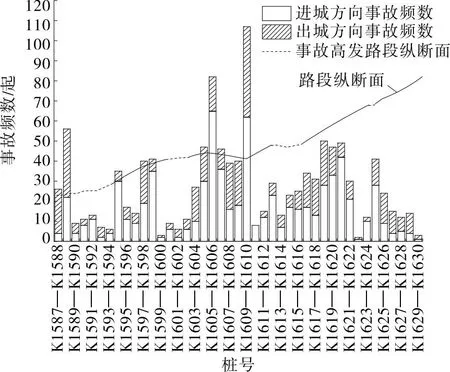
图3 事故频数空间分布特征

交通事故数量在空间上的分布不均匀。将事故当量法和累计曲线法相结合进行事故多发路段鉴定。事故当量法根据事故造成的后果(如死亡人数、受伤人数、经济损失等)将事故按式(1)转化为当量事故,由于交通事故数据没有具体量化经济损失,事故当量化时主要考虑伤亡人数。

QEQ=Q+k1D+k2I

(1)

式中:QEQ为当量事故数;Q为事故发生数量;k1为死亡人数的权重系数;D为事故中死亡人数;k2为受伤人数的权重系数;I为事故中受伤人数。

k1、k2的取值由交通事故给社会带来的负面影响所决定,k1通常取1.5～2.0,k2通常取1.2～1.5,取值大小反映其影响大小。k1取2.0,k2取1.5,得到事故当量化公式如下:

QEQ=Q+2.0D+1.5I

(2)

累计频率曲线法将道路进行单元划分,划分单元长度可取0.20～16.00 km。对于山区高速公路,推荐单元长度取0.05～1.40 km[21],本文取1.00 km。通过计算,将当量事故数由大到小排列,统计各事故当量数单元道路的频率,绘制图5所示当量事故累计频率曲线。

对当量事故累计频率进行二次求导,所得零点即为当量事故突变点。在突变点上方,累计频率虽在增加但事故次数不断减少;在突变点下方,事故次数急剧上升,将事故数超过突变点对应当量事故数的路段作为事故多发路段。进城方向当量事故数突变点在23.5处,出城方向在10.5处,进城方向当量事故数大于23.5起的路段单元为事故多发路段单元,出城方向当量事故数大于10.5起的路段单元为事故多发路段单元。将相邻的事故多发路段单元进行拼接,得到事故多发路段(见表2)。

对于互联网企业来讲，管理层要转变观念，认识到员工培训的重要性。同时要对公司全体员工展开宣传教育，使其明白培训的重要性，不可再令公司的教育培训流于形式。

图5 当量事故累计频率曲线

表2 事故多发路段

2.3 事故所在道路线形分布特征

交通事故与道路线形的关系见图6。从由图6可以看出:1) 事故率与平曲线半径呈“双驼峰”分布,小半径曲线(700～800 m)处交通事故发生率最大,随着平曲线半径的增加和行车视距的提升,交通事故率有所下降;曲线半径为1 200～2 200 m时,驾驶员认为行车条件良好,放松警惕超速驾驶,交通事故发生率增大;曲线半径大于2 200 m时,交通事故率逐渐下降,最终保持相对稳定。2) 大纵坡(-4.0%～-3.0%和3.0%～4.0%)和小纵坡(-1.0%和1.5%)处事故发生率较高。主要原因是在长大纵坡处车辆保持较高速度行驶容易驾驶失控,在小纵坡处驾驶员放松警惕提高速度,事故发生率提高。

图6 事故所在道路线形分布特征

2.4 事故形态分布特征

路段交通事故形态多因素分布特征见图7。由图7可知:追尾、撞击固定物及侧翻是交通事故主要类型,追尾事故占比远高于其他事故。高速公路上车速普遍较快,且行驶途中可能受到车辆故障、驾驶员心理和经验等因素影响,追尾事故频发,追尾是产生人员伤亡的主要事故类型。2) 小汽车发生事故的频次远高于其他车型,其中进城方向小汽车事故占67.96%,货车事故占24.14%;出城方向小汽车事故占70.54%,货车事故占25.92%。小汽车、货车是发生交通事故的主要车型。

图7 事故形态与事故涉及车型分布特征

3 基于树增强朴素贝叶斯模型的事故严重程度影响因素分析

3.1 事故严重程度影响因素选取

山区高速公路交通事故数据具有结构复杂、多属性、多层次的特点。通过分析2016—2020年该路段1 169起交通事故数据,从交通系统的角度将事故严重程度影响因素分为车辆、道路条件、行车环境和事故形态4个属性,采用分层思想从4个分类属性中选取潜在风险因素。道路因素根据JTG B05—2015《公路项目安全性评价规范》[22]将道路线形按表3中标准划分为平直路段、平曲线路段、陡坡路段和弯坡组合路段。山区高速公路受地形限制存在较多长大纵坡路段,采用表4所示标准确定山区高速公路长大纵坡[23]。将属性变量编码作为虚拟变量,建立属性变量集F={X1,X2,X3,X4,X5,X6,X7,X8,X9},并进行离散化取值(见表5)。将交通事故严重程度划分为一般事故、受伤事故和死亡事故三类,事故严重程度用T表示,一般事故取1,受伤事故取2,死亡事故取3。

表3 道路线形划分标准

表4 山区高速公路长大纵坡界定标准

表5 因素属性及取值

3.2 事故严重程度的贝叶斯网络构建

贝叶斯网络是由节点、弧线和概率组成的有向无环图结构模型,主要通过学习不完全、不精确或不确定的知识或信息来推理叶节点和根节点之间的因果关系。输入结构的变量表示网络中节点,用有向弧线连接父节点指向子节点,设变量集合V={X1,X1,…,Xn},Parent(Xi)表示变量Xi父节点的集合,则Xi的条件概率P(V)为:

(3)

节点由表5中风险因素变量表示,变量取值代表节点状态,不同节点状态间的关系用条件概率P(V)表示。通过调整变量某个状态的概率来更新对应父节点的状态信息E,利用贝叶斯理论推断其他节点的概率变化如下:

(4)

利用SPSS Modeler软件比较贝叶斯网络中树增强朴素贝叶斯模型(TAN)、马尔可夫结构模型(Markov)和特征马尔可夫结构模型(FS-Markov),通过评估和分析3种结构模型的正确率和收益确定分析模型。如图8所示,3种结构模型中树增强朴素贝叶斯模型的准确率和收益最高。以贝叶斯网络为基础的树增强朴素贝叶斯网络模型使用最大加权生成树构建属性网络,计算节点间的互信息,根据互信息产生影响关系和权重,遵循已选边不组成回路的原则,构建最大权重生成树,允许预测的每个变量除关联目标变量外还依赖其他预测变量,从而有效增加贝叶斯模型的准确程度。因此,构建图9(a)所示山区高速公路事故严重程度树增强朴素贝叶斯结构,在Netica软件中完成贝叶斯网络模型构建和参数学习[见图9(b)]。

图8 3种测试模型的正确率和收益

图9 山区高速公路事故严重程度贝叶斯网络

3.3 事故严重程度影响因素分析

在贝叶斯网络结构中,多因素组合引发的交通事故概率往往大于组合内单因素单独作用引发的交通事故概率,表明多因素组合作用会增大事故发生频率。通过分析交通事故分布特征和车路耦合作用下事故发生概率,利用树增强朴素贝叶斯结构模型对事故车型和路段线形组合作用、路段线形和事故形态组合作用、事故形态和事故车型组合作用下艰险山区高速公路交通事故严重程度的后验概率进行分析。

车型单独作用与车型和道路线形组合作用下事故严重程度后验概率对比见表6。由表6可知:小汽车和货车发生在平曲线路段、陡坡路段、弯坡组合路段和长大纵坡路段的事故多为死亡事故,涉及货车的事故往往会产生较大财产损失,在山区高速公路不良线形路段发生交通事故易引发人员伤亡。

表6 事故车型与路段线形组合作用下事故严重程度的后验概率

事故形态单独作用与事故形态和路段线形组合作用下事故严重程度的后验概率对比见表7。由表7可知:发生在平直路段和平曲线路段的追尾事故易造成人员受伤,在陡坡路段、弯坡组合路段和长大纵坡路段发生的追尾事故多为死亡事故且会带来财产损失;在平直路段发生撞击固定物的事故,会造成财产损失;在弯坡组合路段和长大纵坡路段易发生侧翻事故,且造成人员死亡的概率较大;在不良线形路段,出现在行驶环境中的所有路侧设施和障碍物都会在交通事故发生时对交通参与者构成严重威胁。

事故形态单独作用与事故形态和车型组合作用下事故严重程度的后验概率对比见表8。由表8可知:涉及多种车型的追尾事故多为受伤事故且会带来财产损失,涉及货车的撞击固定物的事故造成人员死亡的概率增大。固定物如墙壁、树木或混凝土护栏等一般没有安全性能设施(如安全气囊或防护结构),当车辆以较高速度与这些固定物发生碰撞时,冲击力更大,导致车辆和乘客受到更严重的伤害。撞击固定物事故发生时乘客容易因车体变形、扭曲而受到挤压,人员伤亡的概率增大。货车是发生侧翻事故的主要车型,且发生侧翻路段线形条件较差,侧翻事故后,车辆可能会倾斜或完全翻转导致乘员难以逃离,人员伤亡的概率增大。

表7 事故形态与路段线形组合作用下事故严重程度的后验概率

表8 事故形态与车型组合作用下事故严重程度的后验概率

3.4 事故严重程度影响因素的敏感性分析

在贝叶斯网络中,敏感性分析是用来评估输入变量对输出变量影响程度的方法,当网络中某一节点的状态发生改变时,分析该节点对其他节点的影响程度。通过敏感性分析,判断各节点的敏感值大小,依据敏感值探寻网络结构中影响目标节点的关键节点,进而有针对性地把控风险构件。分析叶节点对根节点的影响程度,结果见表9。相关度信息代表根节点对各叶节点的依赖程度,数值大小表示敏感性大小。如果对于某个风险因素的敏感值较大,则该风险因素的微小变化可能会导致目标节点后验概率的大变化。如果敏感值很小,则即使风险因素发生较大变化,对目标节点的后验概率也几乎没有影响。由表9可知:事故涉及车辆数量、事故形态、事故发生月份、事故发生时天气和事故车型是艰险山区高速公路事故严重程度的高敏感因素。通过敏感性分析,可以确定对事件发生概率影响较大的基本节点,进而采取有效措施降低这些基本节点的概率,从而降低事件的发生概率。

4 结语

基于包茂高速公路南环立交至大观互通段1 169起交通事故数据,分析交通事故在时间、空间、路段线形、涉及车型、事故形态方面的分布特征,并利用树增强朴素贝叶斯结构模型对事故严重程度影响因素进行分析。主要结论如下:

表9 事故严重程度贝叶斯网络节点敏感性分析

(1) 该路段2017—2019年的交通事故数量呈逐年增长趋势,受新型冠状病毒感染疫情的影响,2020年交通事故频数最高,2017年单起事故死伤人数最高,1月、8月和10月,9:00—11:00和13:00—16:00是事故高发期。

(2) 艰险山区高速公路事故多发路段集中于隧道路段、互通和不良线形路段;事故形态主要为追尾、撞击固定物和侧翻;小汽车和货车是多发事故的主要车型。

(3) 在事故与路段线形分布上,事故发生频数随平曲线半径的增大而减小,平曲线半径为小半径(700～800 m)和1 200 m时,事故发生频数较高,下坡路段事故比上坡路段事故多发。

(4) 在艰险山区高速公路不良线形路段发生交通事故易引发人员伤亡,不良线形路段条件下出现在行驶环境中的所有路侧设施和障碍物都会在交通事故发生时对交通参与者构成严重威胁。

(5) 事故涉及车辆数、事故形态、事故发生月份、事故车型和天气是影响艰险山区高速公路事故严重程度的关键因素。

根据上述分析,提出如下减少山区高速公路交通事故的对策:实行客货分离,特别是重载货车的分离,大货车靠右行驶,保证同车道内车辆速度差较小;对于长距离不可变车道,在车道驶入端实行客货分流,对长实线路段提前进行预告,通过减少车辆交织降低事故参与车辆数;对于不利天气带来的影响,利用车路协同技术,利用路侧系统监测道路天气状况并将天气信息传递给交通参与者,实现对不利天气的预防;将小半径曲线上坡路段设置为不可变道路段,减少车辆在弯道内部的交织;利用车路协同技术,运用V2V通信技术赋予驾驶员超视距能力,在一定程度上减少由于视距不佳导致的小半径曲线路段交通伤亡事故。