基于频域分析的PMSM双闭环PI控制器整定方法
江腾耀,李伟,朱超,王伟伟,杨蕴萌,邱照原
(1.西北机电工程研究所,陕西 咸阳 712099;2.陆军西安军事代表局驻咸阳地区军事代表室,陕西 咸阳 712000)
目前,工程上PI控制的双环调速系统已在火炮指向稳定跟踪系统中被广泛采用。该系统在工作时会受到炮口振动、路面激励等因素的影响,而PI控制器的参数设计直接影响到不同工况下调速系统的稳态跟踪能力和响应速度,为此有必要对PI参数的精确整定方法进行研究。
火炮稳定指向跟踪系统中电流环控制器主要采用PI控制,其参数采用零极点对消和期望极点配置设计方法,转速环PI控制器则采用最佳中频带宽并与前馈相结合的复合控制[1-2]。然而,上述整定方法并没有直观地描述PI参数与系统频域、时域性能间的联系,若PI参数设置不当会严重影响系统的性能。而通过试错法选择性能令人满意的PI控制器参数在许多场合是不合适的,将干扰因素考虑到模型中,通过一定的约束来界定参数的取值更为有效且合理[3]。文献[4-6]将不确定性和各种扰动视为总扰动,应用扰动观测器来估计其影响,并用于PI参数的整定;文献[7-8]采用了基于多变量滑模极值搜索的PI整定方法,实现了快速准确的跟踪响应、高干扰抑制和对PMSM参数变化不敏感。以上整定方法均为在线整定方法,在一些工况中难以应用,目前以时域指标结合频域参数的分析方法仍然具备很大的工程价值。文献[9]在将PMSM调速控制系统简化,得到了PI参数解析计算公式;文献[10-11]在频域完成了对PI参数的设计,并建立了较为精确的PMSM调速系统;文献[12]采用了在w′域内进行参数设计的离散化方法,直接利用工程经验公式将时域指标转换成开环频域特征量,降低了系统设计的复杂性。上述文献在设计电流环时没有充分考虑到忽略反电动势的条件,在转速环设计中均将阻尼系数视为一个精确恒定的值,因此需要一种更为泛用的方法,在考虑反电动势的同时忽略掉阻尼系数的影响。
笔者通过PMSM双环调速系统的频域分析,推导了电流环与转速环PI参数的解析表达式,建立了PI参数与频域特征量的直接联系。通过合理的简化,给出了双环的简化整定方法,并结合实际工程的需要以及设计过程中的各项约束条件,给出了开环截止频率和相位裕度的取值范围。在实际使用中可以根据电机工作情况下所需要的最大负载转矩,充分考虑转速环允许的超调量后对开环频域特征量合理取值,进行反计算得到相应的控制器参数,从而提升系统的鲁棒性。最后,仿真和实物验证了本文设计方法的有效性。
1 PMSM双环调速系统数学模型
1.1 PMSM模型
对于表贴式PMSM,在d-q旋转坐标系下,Ld=Lq=L,采用id=0控制策略,PMSM的电压方程、转矩方程以及机械运动方程可分别表示如下:
(1)
(2)
(3)
式中:ud0、uq0为未解耦的d-q轴电压;id、iq为d-q轴电流;R、L分别为定子绕组电阻和电感;ωe为电机电角速度;ωm为电机机械角速度;ψf为永磁体磁链;pn为极对数;Te为电磁转矩;TL为负载转矩;Kt为转矩常数;B为阻尼系数;J为转动惯量。
对式(1)~(3)中的q轴交叉耦合电动势进行解耦,令uq=uq0-ωeψf,并假定电机在空载(TL=0)情况下启动,再对式(1)与式(3)进行拉普拉斯变化,得PMSM的解耦模型为
(4)
(5)
1.2 电压源逆变器模型
电压逆变器的基本模型可以等效为一阶惯性环节,开关周期为Ts;死区时间、开关延迟和数字控制延迟可以等效为一个延时环节e-sTd[13],且满足Td≪Ts,则逆变器的传递函数为
(6)
1.3 滤波器模型
由于高频噪声的影响,对电流以及速度进行采样后,需要经过滤波环节才可使用,否则电机控制效果会变差。对电流反馈和速度采用做一阶低通滤波,其各自对应的传递函数为
(7)
(8)
式中:Tcf为电流反馈滤波时间常数;Tsf为速度滤波时间常数。
综合以上环节,可以得到如图1所示PMSM双环调速系统的控制框图,图中Ke为反电动势常数,Kt为转矩常数。

2 电流环设计
2.1 频域法确定电流环PI控制器参数的解析式
在频域内分析、设计控制系统,常以开环频域指标作为依据,而更为直观的体现控制系统性能的则是闭环系统的时域指标。对于高于三阶的系统,难以准确推导出截止频率ωc、相位裕度γ与调节时间ts、超调量σ的关系,因此一般采用在实际工程中总结出的经验描述开环频域指标与闭环时域指标的关系。一般地,γ越大,σ越小,且当γ给定时,ts随着ωc增大而减小[12],系统的开环截止频率和相位裕度直接影响闭环系统调节过程的快速性和平稳性,笔者针对电流环PI参数的设计思路就是通过合理的开环截止频率ωcc和相位裕度γc来满足闭环系统动态性能要求。

将粘性阻尼B带来的扰动和负载转矩TL均视为总扰动D(s)的一部分,通过简化得到图2中的反馈回路。在图2中,由转速引起的反电动势相比电流环来说是个慢动的扰动,只要电流环的带宽足够大,即可忽略E(s)的变化。分析电流环忽略反电动势的条件,忽略D(s)的影响,并考虑反电动势,得到系统闭环传递函数为
(9)

(10)
(11)

(12)
Gc_ol(s)=Gc_PI(s)Ginv_d(s)Gc(s)Gcf(s).
(13)
对于给定的截止频率ωcc和相位裕度γc,引入中间变量:
(14)
Hc_p=arctan(Tsωcc)+
arctan(Tdωcc)+arctan(Tcfωcc),
(15)
(16)
(17)
得到给定截止频率ωcc和相位裕度γc时kc_p2、kc_i2的解析解:
(18)
根据式(18),在ωcc的值确定时,随着γc的增大,kc_p逐渐增大并存在上确界,kc_i的值会逐渐减小并趋于0;在γc的值确定时,ωcc的变化范围还受式(17)条件的限制,因此使用该方法一般先确定ωcc的值,再确定γc的值。
2.2 电流环PI控制器的简化设计
对电流环进一步分析发现,电流环的模型可以进行一定的简化,即将电流滤波器和逆变器均视为1的比例环节,从而降低电流环PI参数设计的复杂度。电流环的开环传递函数可简化为
(19)
当kc_p、kc_i满足以下条件时:
(20)
此时的开环传递函数简化为一个积分环节,闭环传递函数近似为惯性环节:
(21)
给定阶跃信号时,闭环传递函数的输出单调上升且无超调,通过对PI参数的调节,可以实现给定调节时间的要求。当开环传递函数满足幅频特性为1时,代入式(20)的条件,联立得到理想条件下开环截止频率ωcc与电流环PI参数的关系式:
(22)
此时式(21)在闭环频响特性为-3 dB对应的闭环带宽ωcb满足:
ωcb=ωcc.
(23)
2.3 电流环开环截止频率范围的确定
电流环作为系统的内环,除了满足稳定性条件之外,还需要兼顾动态性能,即实现d、q轴电流的快速跟随,允许阶跃响应有一定的超调。开环截止频率直接影响系统的闭环动态性能,截止频率的选取是电流环设计的关键。由于逆变器工作时易产生复杂的开关谐波,为了降低谐波的影响,希望逆变器工作在系统的高频段[10]。笔者要求电流环截止频率对应的时间在20~200个逆变器工作周期之间,即:
(24)

(25)
当电机转速达到最大值时,工作频率也达到最大,电流环截止频率需要大于该值,电流最大工作频率为2πpnnmax/60。此外,以上分析都是在忽略反电动势的条件下进行的,截止频率需满足式(12)的条件。综上所述,得到电流环期望开环截止频率的有效取值范围为
(26)
2.4 电流环开环相位裕度范围的确定
由于PI控制器对相位具有延迟作用,对于式(13)的传递函数所对应的开环相位裕度,满足:
(27)
不等式(27)右边即为不包含PI控制器时的相位裕度,记为γcmax。
(28)
工程上一般对整定后电流环的超调量有严格限制,根据文献[12]中给出的高阶系统超调量与相位裕度关系图,为使超调量低于20%,取最小相位裕度γcmin=π/3。得到电流环期望开环相位裕度的有效取值范围为
(29)
3 转速环设计
3.1 频域法确定转速环PI控制器参数的解析式
由于电流环的调节速度远远快于转速环,在分析转速环时,可以将其近似等效为一个惯性环节
(30)
为了进一步简化系统设计的复杂度,将粘性阻尼B视为总扰动D(s)的一部分。一方面是由于粘性阻尼是一个受电机实际转速影响而有所变化的参数,精确测定较为困难;另一方面是因为转速环的带宽较小,不精确设计带来的误差影响较小。由此得到图3所示简化后的转速环模型框图。

图3中的转速环开环传递函数为

(31)

(32)
Hs_p=arctan(Tcωsc)+arctan(Tsfωsc),
(33)
(34)
式(34)存在一个约束条件,即PI参数比值大于0,因此在ωsc确定时,给定的γs需满足以下条件:
(35)
可以得到给定截止频率ωsc和相位裕度γs时ks_p2、ks_i2的解析表达式
(36)
3.2 转速环PI控制器的简化设计
对于式(31)中的速度滤波环节和电流环延迟环节,由于转速环截止频率ωsc远小于两者的截止频率,因此在正常工作频段其对转速环的影响很小。若忽略掉两者的影响,式(31)可简化为
(37)
当ks_i=0时,闭环传递函数即近似为一阶惯性环节:
(38)
由于扰动的存在,将积分参数ks_i设为0会使得系统存在一定的稳态误差,在粘性阻尼B较大时不能满足精确跟踪的要求。笔者采用最大相角裕度方法来简化转速环的设计。
令Ttd=Tc+Tsf,对于转速环的低、中频段频响特性,可忽略极小项T4Tsfs2,有
(39)
则转速环开环传递函数可表示为
(40)
这是一个典型II型系统,采用II型系统最大相位裕度的方法进行零极点配置,得到:
(41)
最大相角裕度条件下的ks_p1、ks_i1的解析表达式为
(42)
3.3 转速环开环截止频率范围的确定
本文在转速环开环截止频率范围和相位裕度范围确定环节,将直接沿用电流环设计时的结论,允许转速环存在一定的超调,且满足调节时间为tss<0.5 s(±5%误差带)。

(43)
此时的转速环相当于一个惯性环节,对数幅频特性-3 db对应的闭环带宽ωsb满足
ωsb=ωsc.
(44)
根据工程经验,一阶惯性环节阶跃响应上升至给定值的0.95倍所需的时间tsr约为
(45)
为了避免转速环对电流环的影响过大,转速环的带宽ωsb应远小于电流环的带宽ωcb,考虑充分的余量,令
(46)
综上所述,转速环期望开环截止频率的范围为
(47)
3.4 转速环开环相位裕度范围的确定
由于PI控制器对相位具有延迟作用,转速环相位裕度满足
(48)
不等式(48)右边即为不包含PI控制器时转速环的相位裕度,记为γsmax。

(49)
4 仿真分析
4.1 电流环设计与仿真
仿真和实物所采用的PMSM调速系统参数如表1所示。根据表1中的PMSM电机参数,并根据式(26)可以得到电流环期望开环截止频率的有效取值范围为502.6 rad/s≤ωcc≤3 141.6 rad/s。根据理想情况式(22)所对应的PI参数kc_p1、kc_i1,以及式(18)所得的PI参数kc_p2、kc_i2,ωcc从500~3 000 rad/s不同取值得到表2。

表1 PMSM调速系统参数

表2 不同截止频率时电流环PI控制器参数
由表2可知,当ωcc较小时,两组参数近似相等,当ωcc逐渐增大时,逆变器以及电流反馈滤波的延迟效果也变大,导致两组参数的差别也被放大。
在ωcc=1 000 rad/s条件下,分别取kc_p1、kc_i1和kc_p2、kc_i2作为PI参数,得到闭环响应G1、G2。当忽略掉逆变器以及电流滤波的影响,采用kc_p2、kc_i2作为PI参数,此时系统的闭环响应为G3。以上3种情况的闭环波特图如图4所示,其对应的闭环阶跃响应如图5所示。

从图4可以看出,由于在ωcc=1 000 rad/s条件下两种设计方法的PI参数较为接近,闭环频响特性基本相同,中低频条件下的频响特性基本一致,验证了逆变器开关时间、死区延时以及电流反馈滤波对中低频的影响很小,只在高频段影响系统响应,而实际电流最大工作频率为502.6 rad/s,此时忽略掉了逆变器以及电流反馈滤波的影响是合理的。
从图5中可以看出,两种方法设计的PI参数所对应闭环系统阶跃响应相似,G3的上升时间相比G2较长,但总的调节时间几乎一致,因此,在中低频率时可以忽略掉逆变器和电流滤波的影响,将电流环近似等效为一阶惯性环节。


4.2 转速环设计与仿真
选取电流环闭环带宽ωcb=1 000 rad/s,根据式(47),要使调节时间小于0.5 s,转速环开环截止频率范围应满足6 rad/s<ωsc<50 rad/s。根据式(42)和式(36)得到不同截止频率下两种方法的PI参数ks_p1、ks_i1和ks_p2、ks_i2,以及其采用ks_p2、ks_i2对应阶跃响应超调量σ,如表3所示。

表3 不同截止频率时转速环PI控制器参数
从表中的参数可以看出,式(36)、(42)所得的PI参数几乎一致,其闭环阶跃响应基本一致,这是由于在简化设计中只忽略了一个极小项TcTsfs2,充分考虑到了电流环以及速度滤波对转速环的影响。因此当满足最大相位裕度时,可用ks_p1、ks_i1代替ks_p2、ks_i2以简化PI参数的计算。
开环频率ωsc从2.5 rad/s到50 rad/s取不同值,采用ks_p2、ks_i2作为PI参数,得到图8所示闭环空载阶跃响应图。由图可知,当ωsc≥10 rad/s时,调节时间均满足tss<0.5 s的要求。ωsc越大,响应越快,但是超调也越明显,对电流环的要求也更高;ωsc越小,闭环响应平稳越好,调节时间变长,ωsc过小时由于积分系数非常小,跟踪速度过慢,可能导致转速跟踪存在稳态误差。
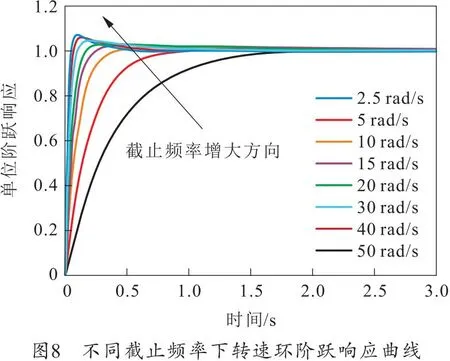


表4 不同相位裕度时转速环PI控制器参数
根据表4得到空载情况下不同裕度下转速环的单位阶跃响应,如图9所示。

对于空载并且忽略掉粘性阻尼的情况下的转速环,在ωsc的值确定时,随着γs的增大,ks_p会逐渐增大,ks_i的值会逐渐减小并趋于0,因此当γs过小时,积分系数较大,系统快速性较好,但超调量明显;当γs增大时,闭环响应的平稳性变好,在γc=γsmax即ks_i2=0时其动态性能最优,无超调且快速性较好,近似为一个一阶惯性环节。
实际的PMSM系统往往是带负载工作的,对转速环的抗扰动能力有更高的要求。图10为具有负载扰动状态下采用表4中的PI参数得到的阶跃响应图,在0 s时负载为3 N·m,在10 s负载增加为5 N·m。由图中波形可知,γs越小,由于积分系数较大,转速环抗扰动性能越强,其回复速度越快;随着γs的增大,积分系数变小,转速环抗扰动回复时间越长,回复的时间与扰动变化量直接相关,给定的扰动越大,所需要的回复时间越长;当γc=γsmax时,系统将存在稳态误差。在实际使用中可以根据电机工作情况下所需要的最大负载转矩,并且充分考虑转速环允许的超调量后对γs合理取值。

5 实物实验
为验证本文整定算法可行性与通用性,在由北京华力创通科技股份有限公司研制的随动控制实时仿真装置上进行实物实验。该系统以DSP 28337D作为主控芯片,整体硬件部署主要包括伺服控制机柜、伺服驱动柜和两个实验台。实验台上安装有电机和目标仿真机的上位机,其中电机的具体参数如表1所示,实验数据通过上位机中的RTSimPlus主控软件导出,采样频率为0.2 ms。

实物实验中的电流环采用1 000 rad/s作为截止频率,采用表2中的参数。图12为令交轴电流iq=0 A时对直轴电流id给定不同阶跃信号后得到的响应图。由图12(b)可以看出,给定8 A的电流阶跃信号,电流环阶跃响应无超调,电流环调节时间约为3 ms,这与设计时给定的截止频率相符合,且电流环具有较好的稳态特性,满足设计要求。

采用表3中的参数,图13为该参数下给定1 000 r/min转速阶跃信号时的空载响应波形。转速环截止频率取10 rad/s时,超调量约为0.5%,调节时间约为0.355 s,与该截止频率理想情况下0.3 s的调节时间相接近。

由于实时仿真装置的控制步长相比理想仿真的步长要大,实际得到的实物响应曲线的超调量略大于设计时的理想值,两者的调节时间基本一致;ωsc=20 rad/s且ki=0时,由于粘性阻尼等干扰的存在,转速环存在稳态误差。图14为给转速环500 r/min以及0 r/min的转速阶跃信号时交轴电流iq的响应。由图14可看出,交轴电流iq可实现参考值iq-ref的快速精确跟踪,空载稳态情况下电流的脉动较为平稳,按该方法设计的PMSM调速系统具有良好的动态性能。

6 结束语
笔者通过对PMSM双环调速系统的频域分析,确立了双环PI控制器参数与其对应的开环截止频率和相位裕度的解析式,并明确了开环频域特征量与闭环时域指标的关系;基于频域法设计双环时的各项约束条件以及对闭环系统的性能要求,给出了双环PI参数的合理取值范围;考虑到电机阻尼系数难以精确测定的问题,对转速环进行了合理简化,并给出了相应的简化设计方法。仿真和实验结果表明,采用频域整定方法得到的系统具有良好的稳定和动态性能,实际使用时可以根据调节时间和最大负载要求选定合适的截止频率和相位裕度来计算需要的PI参数,具有一定的工程价值。

