基于COMSOL的电磁发射一体化弹丸动力学分析

裴畅贵，刘国志，金寅翔，原泽坤，王大为

(1.中北大学 航空宇航学院，山西 太原 030051；2.山西北方机械制造有限责任公司，山西 太原 030051；3.中北大学 机电工程学院，山西 太原 030051)

随着高新技术在智能弹药上的应用,其技术含量越来越高,涉及的技术领域越来越宽。电磁轨道炮作为一种大威力动能发射平台,可以极大提高弹丸的初速和射程,增强威力,是发射智能弹药的新兴发射系统,具有极高的研究价值[1]。

我国学者对电磁轨道炮做了许多研究。早在1984年,沈金华等就介绍了电磁轨道炮的历史、现状及相关结构,并提出了应用的可能[2]。随着科技的发展,20世纪前后,电磁炮逐渐开始深入的研究,周之奎等对电磁轨道炮进行了性能的数值模拟[3],武松涛等对紧凑型电磁轨道炮及填弹器进行了研制[4],胡玉伟通过对电磁轨道炮系统进行建模与仿真,提出了进一步研究方向[5]。在这段时间内,电磁轨道炮展现出了巨大的研发潜力与应用价值。近几年来,针对电磁轨道炮进行的研究更加丰富,贾义政对四轨电磁炮进行了动力学建模与仿真,得到了电枢的运动特性和系统的力学特征[6]。高博等利用ANSYS对电磁轨道炮进行动力学仿真计算,为进一步研究轨道炮特性及身管优化设计提供了参考[7]。成晨针对电磁轨道炮进行了反后坐装置设计并建立了电磁轨道炮的全炮动力学模型,为电磁轨道炮的低后坐技术研究奠定了一定的基础[8]。沈剑建立了电磁炮刚柔耦合动力学模型,考虑了刚柔耦合作用对发射系统的影响[9]。周维等利用Maxwell软件对电磁炮膛内电磁分布与抗干扰性能进行了研究,并提出了有效的解决方法[10]。陈帅等对其他国家在电磁轨道炮方面取得的成果和应用进行了阐述,并对其发展所面临的问题进行了总结[11]。

综上所述,相关学者对电磁轨道炮进行了大量的研究,电磁轨道炮得到了巨大的发展,但针对电磁轨道发射一体化弹丸进行的研究依然较少。笔者针对电磁轨道炮,建立其发射一体化弹丸模型并对其进行动力学分析,得到其连续的、瞬态的受力曲线和磁场特性,深入分析弹丸在电磁发射过程中的动态行为和磁场特性,对于提升弹丸性能和设计优化具有关键作用,同时为一体化弹丸在多物理场条件下的研究提供一定的技术支持和理论依据,推动未来智能武器技术的发展。

1 数学模型

1.1 发射系统电磁理论

电磁发射实际上是以电磁引起的力学变化,所以首先需要从电磁场强度的计算开始研究。

麦克斯韦方程组是描述电流激发电磁场运动规律的方程组,其微分的形式描述如下：

(1)

式中：D为电位移矢量;ρf为电荷密度;B为磁感应强度矢量;E为电场强度矢量;H为磁场强度矢量;Jf为电流密度矢量。

计算两条轨道在电枢位置的磁场密度是计算电枢受力的前提,因此建立如图1所示的电枢磁场计算坐标系。图中h为轨道高度,d为轨道宽度,b为两轨道之间的距离,h′为电枢高度,ld为电枢的长度。

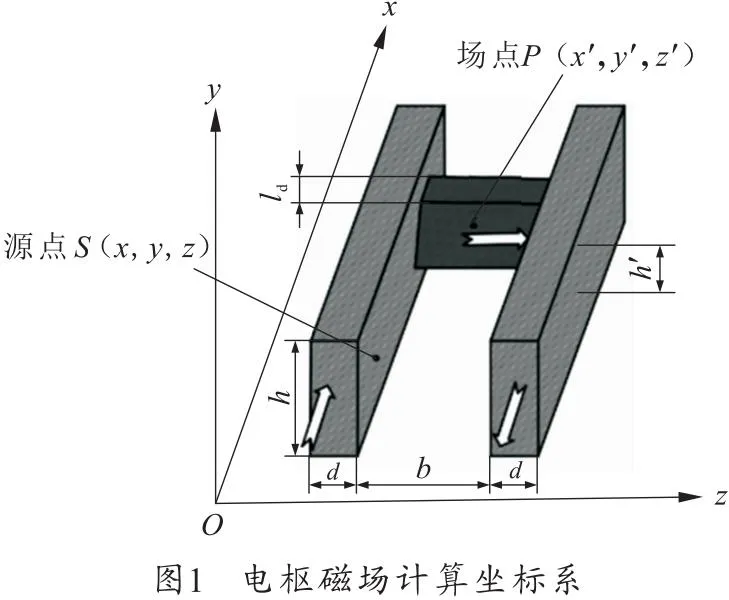
设电流源点为S(x,y,z),场点P(x′,y′,z′)。假设在电枢和轨道内电流均匀分布,则对于轨道体电流分布形式下,J′v为体电流密度,电枢电流元为J′vdxdydzk,左轨道电流元为Jvdxdydzi;右轨道电流元为-Jvdxdydzi。

当轨道、电枢、弹丸中通有体电流时,左轨道电流源点坐标为S(x,y,z),电枢上场点坐标为P(l(t),0,0)。则P点产生的y方向上的磁感应强度为

(2)

由此可以得到轨道体电流在电枢位置产生的磁场密度。

计算在电磁轨道系统中任意一点P的磁场密度,是发射过程中的研究重点,因此建立任意磁场计算坐标系,如图2所示,l为电流回路长度,(xp,yp,zp)为P点坐标,假设电枢位移的距离为2l,电流由轨道1进入,由轨道2返回,两轨迹关于xOz平面对称,线电流也位于yOz平面上,原点位于轨道的初始部位。

考虑S点处的电流元Idl在空间P点产生的磁感应强度为

(3)

式中：μ0为真空磁导率;I为流经轨道的电流强度;dlj为导体的长度元;Rj为由S至P的距离;Rj为R方向的距离矢量。

(4)

式中：

同理可得,轨道2在P点产生的磁感应强度为

(5)

式中：

将式(4)、(5)对z在[0,2l]积分可得两轨道在P点产生的磁感应强度。

除了两轨道对P点产生电磁效应,还有电枢电流源点对P点有电磁效应。电枢坐标为(0,y,2l),y为变量,则有Idl3=Idyj;同理可得电枢在P点产生的磁感应强度为

(6)

式中：

1.2 电磁发射系统力学理论

发射系统中的受力分别为一体化弹药受力和轨道受力。一体化弹药受到电磁力和摩擦阻力,轨道受到两轨之间的相互作用力及电枢对轨道的电磁力。

根据通过电枢的电流可以计算出电枢上任何位置受到的电磁力,电枢在磁场中的受力为

dF=∮Idl×B,

(7)

因此,根据体电流计算,便可得电枢受到电磁驱动力沿轨道方向的推力为

(8)

由于两轨道之间的电流流动方向相反,因此轨道间就有相互作用的排斥力。

(9)

根据电磁力公式dF=∮Idl×B可得轨道1单位长度所受的力为

(10)

由式(10)可以看出,力的方向与j的方向相反,即是斥力。因此轨道1上的单位面积所受的力大小为

(11)

1.3 电磁轨道发射系统三维模型

电磁轨道发射系统模型如图3所示。工作时,电流经过一条轨道,在流过电枢后,流入另一条轨道,形成闭合回路。当强脉冲电流接入轨道时,其周围产生强大的电磁场,与流经电枢的电流相互作用产生电磁力,推动电枢和置于电枢前的一体化弹丸做加速运动[12]。

根据电磁轨道炮发射系统的工作原理,可知一体化弹药结构克服与轨道间的相互摩擦力受到电磁推力的作用,轨道受到电磁斥力的作用,而发射身管则受到由轨道传递过来的力和电枢高速运动过程中所产生的动力。在发射载荷的作用下,发射过程是一个复杂的动力学过程[13]。

1.4 一体化弹药模型

运用模块化建模方法建立各个部件的模型,为了使弹托便于脱落,设计成四瓣分离式弹托,弹托外表面呈长方体,保留具有承载高载荷的梁结构,对外表进行拓扑,减轻质量的同时,起到固定支撑的作用[14]。一体化弹药的总体结构如图4所示。

一体化弹丸的尺寸为30 mm×30 mm×126 mm,采用30 mm口径电磁轨道炮发射。弹丸出膛后,在空气阻力的作用下,弹托迅速脱落,导引头接收到目标发射回来的激光信号,经弹载芯片计算处理后,由控制器控制电磁舵机方向,实现4个尾翼的偏转变向,从而改变飞行轨迹,精准命中目标。弹丸的外径、质量和体积较小,弹体部分由弹钢材料和核心模块组成。发射时弹托对弹丸的定心引导起关键作用,可以有效减小弹丸的冲击载荷。弹丸结构如图5所示。

1.5 材料参数

整个电磁轨道发射装置由轨道、电枢、弹芯、弹载芯片、弹托等组成,主要对电磁轨道炮发射一体化弹药进行模拟仿真,由于分析的弹丸需要在高过载下在轨道内做加速运动,这就对发射系统各组件的结构强度有更高的要求,因此各个组件的材料参数需要认真选择,多以弹塑性材料模型为主[15]。

轨道作为大电流的载体不仅需要耐磨损耐烧蚀,还需要有良好的导电性,因此选用铜合金[16]。电枢和弹托材料均选用高强度铝合金,密度小、强度高、能受热,可以减少身管内壁的磨损。弹芯部位主要是增加弹丸前部质量,所以采用密度较高,强度较大的弹钢材料。芯片材料使用FR- 4材料,是电子元件的通用材料之一,具有较好的耐热性。战斗部采用B炸药的材料参数。结构场和电磁场材料参数如表1所示。

表1 结构场材料和电磁场材料参数

2 有限元分析

2.1 有限元建模

笔者以电磁轨道炮为研究对象,建立包含导轨、电枢的有限元模型,进行一体化弹药在膛内运动数值计算。电磁发射过程中,一体化弹药四周的棱角会对仿真结果产生极大的影响,并且棱角的存在会加大网格划分的难度,并增加计算时间,因此,对一体化弹药的四周进行倒角,忽略可能造成体载荷误差的横向沟槽,忽略螺纹连接,忽略弹载芯片上的表征结构,忽略模块与模块之间的导线。建立空气域得到周围的磁场强度等特征,建立无限空域作为研究区域的外层用以模拟无限远空间,建立弹丸运动域控制弹丸运动方向。电枢弹丸在膛内运动,因此对模型进行切块,方便对动网格的设置,具体如图6所示,轨道尺寸为20 mm×40 mm×3 000 mm,空气域半径300 mm。

在进行网格划分时,调用COMSOL软件内自集成的动网格接口,动网格的网格质量不随网格数量的增加而增加。各模块的几何模型与有限元网格模型如图7所示。

2.2 激励电流设置

选取文献[17]中的双指数脉冲电流作为激励电流源,该脉冲电源可以在几毫秒内提供数兆焦耳电能[7]。表达式为

I=a·(e-bt-e-ct),

(12)

式中：a为1.449 A;b为504 s-1;c为4 862 s-1。电流波形如图8所示,计算时长为3 ms,在0.5 ms时达到1 MA的电流峰值。

使用COMSOL对图8所示的双指数脉冲电流作傅立叶变换,得到图9(a)所示的电流幅频特性,可以看出脉冲电流的频率主要集中在5 kHz以下的低频段。

同样使用COMSOL对图8的脉冲电流作Hilbert变换得到电流时频特性,如图9(b)所示,由此可知,在脉冲电流放电过程中,双指数脉冲电流频率低于1 kHz,并且频率下降迅速,因此电磁轨道发射磁场为低频强磁场。

由电磁发射原理可知,轨道的一个端面需要接地,轨道的另一端面需要终端通电。两条轨道均电流守恒,电传导模型为电导率传导模型。电磁发射过程需要设置一体化电枢与轨道接触面的电接触,电接触加载条件为收缩传导率hc为C-M-Y(Cooper-Mikic-Yovanovich)相关性,表面粗糙度中粗糙平均高度为1 μm,表面粗糙度粗糙平均斜率为0.4,接触压力为计算量,微硬度为3 GPa。由于ODE方程为动态公式,在本计算的感应传导在数值上非常重要,这意味着亥姆霍兹矢量方程需要被打开,即A场规范固定。因此,笔者在磁场设置中添加了磁失势规范固定,并对所要计算的电枢添加了力计算,电磁耦合产生电流的方式为外部电流密度,根据电流守恒定律,电流密度公式为

(13)

式中：Jx、Jy、Jz分别为x、y、z方向电流密度分量;Jdx、Jdy、Jdz分别为x、y、z方向的位移电流密度分量;Jex、Jey、Jez分别为x、y、z方向的外部电流密度分量;Jix、Jiy、Jiz分别为x、y、z方向的传导电流密度分量,为

(14)

式中：σ为导率分量;E为电场分量。

电流密度设置如图10所示。

2.3 ODE方程与动网格设置

针对电磁轨道发射系统的理论方程,调用软件中的全局常微分方程,对动网格进行编辑处理。

当电枢位置发生改变后,需要重新嵌套描述系统特性的数学模型,然后再次对系统进行计算。因此,在计算电磁发射的过程中,调用全局常微分方程,即ODE方程,对一体化电枢设置动网格,建立电磁轨道炮发射一体化弹丸模型。使用全局常微分和微分代数方程接口和逻辑表达式来指定用于描述速度和位置的微分方程。根据牛顿第二定律,可得电磁力

F=ma,

(15)

式中：a为弹丸运动的加速度;m为一体化弹丸的质量。

COMSOL全局方程需要定义电枢运动的速度v,速度v可由电枢运动的加速度a对t积分求得。

根据能量守恒原理,电磁发射系统的电磁能增量为

(16)

电磁力F的表达式为

(17)

式中：x为整个弹丸位移量;L(x)为电感量;I(t)为电流大小;L′为电感梯度。由此可以看出,弹丸受力F与电流的平方和电感梯度相关,不随弹丸位置变化而变化。

因此,在COMSOL全局方程中定义：

(18)

(19)

由此求出弹丸运动速度v,弹丸位移量x：

x=vt.

(20)

输入如图11所示。图中,S1为电枢的运动位移;V1为S1的微分即电枢的运动速度;a为V1的微分即电枢的运动加速度。

此ODE方程建立在基本运动方程之上。以洛伦兹力F作为源物理量,电枢位移S1作为因变量物理量,加速度a由电枢受到洛伦兹力F除以电枢弹丸质量求得。

动网格设置如图12所示。

3 结果分析

3.1 动力学分析

利用COMSOL瞬态求解器求解一体化弹丸的动力学特性,得到连续的、瞬态的一体化弹丸的受力曲线、速度曲线和位移曲线,如图13所示。

一体化弹丸受到电磁驱动力、摩擦力及空气阻力的作用,由图13(a)可以看出,一体化弹丸受到的电磁推力与理论曲线相符合。当电枢速度较低时,滑动摩擦力对电枢运动起主要阻碍作用,在发射过程中,电流源与一体化弹药的电磁力变化规律一致,且在电流峰值时刻达到最大值,为325.77 kN。由于空气阻力与电枢速度的平方成正比,因此,在电磁轨道炮发射后期,当电枢速度较大时,空气阻力成为弹丸的主要阻力。

由一体化弹丸速度曲线可知,在3 ms时刻达到最大值,为1 346 m/s。此外,一体化弹丸的加速度变化是先增大后减小的,在发射前期,作用于一体化弹药的电磁力远远大于电枢所受阻力,电枢速度上升很快,激励电流幅值变小,电磁力小于电枢阻力,使得电枢加速度有所下降。由电枢位移变化曲线可知,在双指数脉冲激励电流放电结束之前,一体化弹丸位移了2 576.5 mm。

3.2 电磁特性分析

图14、15为发射过程中每0.5 ms的电流密度及曲线。

通过轨道间的电流密度流线图和电流密度模曲线,可以直观地看出发射系统中的电流稀疏程度和相对滑动导体材料间的电流瞬态扩散现象,80%的电流聚集在5%的轨道深度并从狭窄的分布区域流入电枢。由于存在运动速度,模型中的电流集中在一体化电枢和轨道接触面靠近电枢后侧、电枢喉部和弹托与电枢的接触面,这种典型的现象成为速度趋肤效应,电枢速度越快效应越明显。

4 结论

笔者采用基于COMSOL的电磁场仿真模拟方法,结合理论推导和数值计算,对电磁发射一体化弹丸的动力学行为和电磁特性进行了系统的研究。通过建立弹丸发射有限元模型并利用COMSOL软件进行仿真,分析弹丸在电磁场中的受力情况,得到了弹丸在电磁发射过程中的速度和位置等关键参数,并对其电磁特性进行研究。理论分析及仿真结果表明：

1)在一体化弹丸发射过程中,当电枢速度较低时,滑动摩擦力对电枢运动起主要阻碍作用。在发射过程中,电流源与一体化弹药的电磁力变化规律一致,且在电流峰值时刻达到最大值。由于空气阻力与电枢速度的平方成正比,因此在发射后期,当电枢速度较大时,空气阻力成为弹丸的主要阻力。

2)一体化弹丸的加速度变化是先增大后减小的,在发射前期,作用于一体化弹药的电磁力远远大于电枢所受阻力,电枢速度上升很快,激励电流幅值变小,电磁力小于电枢阻力,使得电枢加速度有所下降。

3)发射系统中,80%的电流聚集在5%的轨道深度并从狭窄的分布区域流入电枢,模型中的电流集中在一体化电枢和轨道接触面靠近电枢后侧、电枢喉部和弹托与电枢的接触面,形成了速度趋肤效应,电枢速度越快效应越明显。

通过深入理解电磁发射一体化弹丸的动力学行为和电磁特性,本文得到了相关的结果并可为电磁发射技术的进一步发展提供重要的参考和指导。