基于改进小波阈值的自行火炮信号降噪方法研究

刘子昌，白永生，贾希胜

(1.陆军工程大学石家庄校区，河北 石家庄 050003；2.河北省机械装备状态监测与评估重点实验室，河北 石家庄 050003)

柴油发动机(以下简称柴油机)作为陆军现役装备中自行火炮、坦克、装甲车辆等武器装备的动力系统,一旦出现故障会产生严重的后果。由于其运行环境复杂,各个部件相互干扰,各种非线性、非平稳信号彼此严重重叠,导致利用传感器采集到的振动信号不可避免地被噪声污染。含噪声的信号使得后续分析受到干扰甚至失效,尤其对于早期故障来说,噪声的影响会更大。通过对原始信号进行降噪预处理,有助于提取反映自行火炮柴油机运行状态的关键特征,从而提升振动信号的有效利用率。因此,对采集到的原始振动信号进行降噪处理十分必要,对于预防突发事故、降低维修费用和提高其运行效率具有重大意义[1]。

常用的信号降噪方法包括经验模态分解(empirical mode decomposition, EMD)及其衍生算法、小波阈值降噪等。Sha等[2]提出基于差分EMD和极值场均值模态分解的降噪方法。但EMD具有端点效应、模态混叠等不足。Niu等[3]提出基于互补集合经验模态分解和双边滤波的降噪方法,利用双边滤波对分解后噪声占主导地位的分量进行降噪。Zhou等[4]提出结合自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)和噪声量化策略的降噪方法,通过噪声评估的周期性调制量化各分量的噪声。尹逊龙等[5]研究了基于深度变分模态分解的振动信号降噪方法,具有良好的鲁棒性。但是,仅通过这类方法对原始信号分解后重构精度较低,难以判断分解后各分量的随机性,且没有对需要降噪的分量进行降噪处理。由于小波阈值降噪计算量小、可从频域和时域角度分析信号,广泛应用于振动信号降噪领域。董鑫等[6]提出用于一维振动信号分析的谱图小波阈值降噪方法,降噪信号平滑度高、畸变小。Zhang等[7]提出一种将小波阈值与EMD相结合的降噪方法,以提高低信噪比下振动信号的降噪性能。梁春辉等[8]将粒子群优化算法和禁忌搜索算法融合后引入多小波相邻系数去噪方法中,改进其阈值求取方式。但是,通过小波软阈值处理后的小波系数和真实小波系数存在偏差,重构信号时误差增大;硬阈值函数不连续,降噪后可能会产生振荡[9]。

基于上述分析,笔者提出基于改进小波阈值的振动信号降噪方法。首先,运用改进的自适应噪声完备集成经验模态分解(improved complete ensemble empirical mode decomposition with adaptive noise, ICEEMDAN)分解原始振动信号,得到各本征模态函数(intrinsic mode function, IMF)分量;其次,通过改进的麻雀搜索算法(improved sparrow search algorithm, ISSA)优化后的多尺度排列熵(multi-scale permutation entropy, MPE)检测各分量的随机性,筛选出需要降噪的分量;然后,使用改进的小波阈值对筛选出的分量进行降噪处理;最后,重构降噪后的分量与无需降噪的分量,得到降噪后的振动信号。通过仿真信号和实验室实测数据验证所提振动信号降噪方法的可行性和有效性。

1 理论分析

1.1 ICEEMDAN

ICEEMDAN的具体步骤如下：

步骤1在原始信号x(t)基础上构造新信号xi(t)：

xi(t)=x(t)+β0E1(wi(t)),i=1,2,…,N,

(1)

式中,β0为可以用来对所需信噪比进行调整的噪声系数：

β0=ε0std(s)/std(E1(wi(t))),

(2)

式中：ε0通常设置为0.2,表示噪声的幅值;std(·)表示求标准差,当k≥1时,βk=ε0std(rk),rk表示第k阶残差;Ek(·)表示信号通过EMD分解后的第k个IMF模态分量;wi(t)表示加入的第i组具有均值为0且方差为1的高斯白噪声,共加入N组。

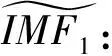
r1=〈M(xi(t))〉,

(3)

(4)

式中：M(·)表示求信号的局部均值;〈·〉表示求平均值的运算。

(5)

步骤4当k≥3时,按照上述步骤可得第k个残差分量rk：

rk=〈M(rk-1+βk-1Ek(wi(t)))〉.

(6)

(7)

步骤6重复步骤4和步骤5,直到获得的残差分量不能够被进一步分解时停止迭代,得到所需各分量。

1.2 MPE

MPE的具体步骤如下：

(8)

式中：j为粗粒化序列编号;N为时间序列的长度;s为尺度因子;[·]表示向下取整。

(9)

式中：τ为延迟时间;l=1,2,…,N-(m-1)τ为重构分量;m为嵌入维数。

步骤3按升序对各重构分量重新排列,可以得到新的符号序列s(v)：

s(v)=(l1,l2,…,lm),

(10)

式中,v=1,2,…,V,且V≤m!。通过该步骤,可以生成m!种不同序列。

步骤4计算各符号序列出现的概率Pv。

步骤5计算各尺度下的排列熵：

(11)

1.3 ISSA

薛建凯于2020年提出了一种寻优算法,即麻雀搜索算法(sparrow search algorithm, SSA),与粒子群算法、遗传算法、蚁群算法等智能优化算法相比,SSA具有更好的寻优效果[10]。但该方法存在易陷入局部最优、收敛速度慢等问题,仍有提升空间。因此,笔者提出了ISSA,通过ISSA对MPE中各超参数进行寻优。与SSA相比,改进的方面有：

(12)

式中：i=1,2,…,N;l和u分别表示搜索空间的下界和上界;Xi=[xi1,…,xid,…,xiD]为初始种群。合并反向种群和随机生成种群之后,得到新的种群,升序排列其适应度函数值,得到所需新的初始种群为排列后前N个最优初始解。

2)SSA中,侦查者负责警戒,防止被捕食,位置更新可表示为

(13)

式中：Xbest为当前全局最优位置;β为步长控制随机数,且该参数服从正态分布;K∈[-1,1]为随机数,用于对步长和移动方向进行控制;ε为用于避免分母为0的常数;fi、fw和fg分别表示目前个体适应度、最差适应度和最优适应度。

由于式(13)中的参数β和K为对局部开发和全局搜索能力进行平衡时具有关键作用的随机数,对参数随机取值容易导致算法陷入局部最优。因此,可通过分别改进参数β和K进行算法优化：

(14)

(15)

式中：fbest和fworst分别为最优和最差的适应度函数值;t和T分别为当前和最大的迭代次数。对原始算法进行优化后,能实现对步长控制参数的动态调整,平衡算法的局部开发和全局搜索能力,以避免陷入局部极值,提高寻优精度。

3)根据文献[11]可得,SSA容易陷入局部极值,导致难以找到全局最优值,使用Levy策略对式(13)进行优化。在寻找最优解过程中,Levy飞行不仅可以在短距离中进行局部搜索还可以在长距离全局搜索。因此,在搜索到最优值附近时,Levy能达到增强局部搜索能力的作用,有效解决标准SSA陷入局部最优的问题。改进后该步骤的表达式为

(16)

式中：

(17)

(18)

式中：d为向量维度;r1,r2∈[0,1]为随机数;β为常数;Γ表示伽马函数;L(d)表示Levy策略的计算公式。通过该策略对SSA算法改进之后,能够在降低陷入局部极值风险的前提下,充分进行局部搜索。

为实现准确筛选需要降噪的分量,应用ISSA对MPE中嵌入维数m、尺度因子s和延迟时间τ等参数进行寻优,实现过程如图1所示。使用偏度的平方作为适应度函数,多次运行后求平均值并取整,得到合理的参数组合。将各参数代入MPE中,计算各分量的MPE值,筛选出需要降噪的分量。

1.4 改进的小波阈值降噪

笔者提出一种改进的小波阈值降噪方法处理需要降噪的IMF分量。小波阈值降噪方法的关键在于阈值的选取,只有对阈值合理选取才能在保留真实信号的前提下有效提升降噪效果。传统的软阈值和硬阈值函数分别为

(19)

(20)

(21)

式中：λ1和λ2表示阈值,λ1=aλ2,本文中a=0.5,用于控制λ1和λ2之间曲线的斜率,使改进后的阈值函数具有较好的灵活性;λ1=σ2lgN,σ=median(|wj,k|)/0.674 5,表示噪声标准差,N为信号长度,median(·)表示求中值运算。

2 基于改进小波阈值的降噪方法

笔者所提的基于改进小波阈值的振动信号降噪方法能够在保留原始振动信号真实成分的前提下,有效且自适应地滤除信号中的噪声,流程图如图2所示。

当前的振动信号降噪方法中,分解原始信号时大多采用EMD或CEEMDAN,而ICEEMDAN与EMD和CEEMDAN相比具有更低的重构误差,分解效果更好,因此,所提方法中使用ICEEMDAN分解原始振动信号。为实现准确筛选需要降噪的分量,提出一种改进的麻雀搜索算法,用于对MPE中各参数寻优,以准确筛选出需要降噪的分量。针对传统小波软、硬阈值降噪的不足,提出改进的小波阈值降噪方法,用于对筛选出的分量降噪,在保留真实信号的前提下有效提升降噪效果。

3 实验验证

分别使用仿真信号和实验室实测数据验证本文提出的降噪方法的可行性及有效性。对比方法均为目前广泛应用的方法,包括小波阈值降噪(对原始信号直接通过小波软阈值方法降噪)、多小波相邻系数降噪(对原始信号直接通过多小波相邻系数方法降噪)和ICEEMDAN-MPE-小波阈值降噪(通过ICEEMDAN分解原始信号,运用MPE分析各分量的随机性,筛选出需要降噪的IMF分量,使用小波软阈值处理需要降噪的分量,重构降噪后的分量和无需降噪的分量)。

3.1 仿真信号验证

通过仿真信号验证所提降噪方法的可行性。由MATLAB生成的原始信号如式(22)所示,共有4 096个采样点,采样间隔设置为1 s,时域波形如图3所示。将信噪比为5 dB的高斯白噪声添加到原始信号中,得到添加噪声后信号的时域波形如图4所示。

(22)

由图3、4可得,原始信号的时域波形清晰,加入噪声后,噪声把原始信号淹没,已难以分辨出原有波形。通过笔者所提新的方法对含噪信号进行降噪处理。运用ICEEMDAN对含噪信号进行分解,得到各IMF分量如图5所示。

由图5可得,含噪信号被分解为12个IMF分量。各分量受噪声的影响随着IMF序号的增加逐渐降低。通过ISSA对MPE各参数寻优,得到最优参数组合为m=6、τ=1和s=12,目标函数值随进化代数变化曲线如图6所示。将各参数值带入MPE中,对各IMF分量的随机性进行分析,得到各分量的MPE值如图7所示。

由图7可得,MPE值随着IMF序号的变大而逐渐降低,表明噪声对分量的影响逐渐减弱,IMF1～IMF4分量的MPE值超过了0.6。通过改进阈值函数的小波阈值降噪方法对IMF1～IMF4分量进行降噪,得到降噪后的各分量。将降噪后的分量与无需降噪的分量重构,得到降噪后的振动信号。通过小波阈值降噪、多小波相邻系数降噪和ICEEMDAN-MPE-小波阈值降噪方法对含噪信号进行降噪,结果对比如图8所示。

由图8可得,通过所提降噪方法对含噪信号进行降噪处理后,降噪效果明显优于其余3种对比方法,与原始信号具有最高的吻合度。图8的对比方法中,仅使用小波阈值降噪方法并不能对信号中的噪声有效去除,多小波相邻系数降噪方法将原始信号中一些真实信号成分剔除,存在降噪过度现象,ICEEMDAN-MPE-小波阈值降噪方法的结果在部分极值点处仍然存在一些毛刺现象,而笔者提出的方法能够在有效滤除噪声的同时更好地保留信号中的真实成分,可以清晰地恢复出原始信号,证明该方法是可行的。

通过对各方法的降噪效果进行定量分析来验证所提方法的有效性。使用信噪比R、均方根误差E和相关系数C对4种不同方法的降噪效果进行定量评价,表达式分别为

(23)

(24)

(25)

信噪比指标反映的是信号与噪声的比值,该指标越高,表示信号与噪声分量之比越大,降噪越有效。均方根误差指标反映的是测量值与真实值的偏差,即降噪信号与原始信号的差别大小,其值越小,表示降噪效果越好。相关系数反映的是信号之间的相关程度,该指标越大,表示原始信号与降噪信号波形越相似,降噪效果越好[12]。各降噪效果评价指标的计算结果如表1所示。

表1 仿真信号的评价指标计算结果

通过对比表1中4种不同降噪方法的评价指标计算结果可知,笔者所提降噪方法在各评价指标上均显著优于其余3种降噪方法,具有最佳的降噪效果。所提方法与小波阈值降噪、多小波相邻系数降噪和ICEEMDAN-MPE-小波阈值相比,信噪比分别提升了5.989 4 、6.078 7 和1.565 3 dB,增益了53.46%、54.69%和10.02%;均方根误差分别降低了0.342 4、0.349 5和0.068 1;相关系数分别提升了0.025 7、0.030 0和0.004 3。综上,使用笔者所提方法对振动信号进行降噪处理是可行的。

3.2 实验室实测数据验证

为了验证笔者所提方法的有效性,依托于实验室的高压共轨柴油机实验台,采集柴油机在运转过程中的状态监测信息。结构如图9所示,柴油机技术指标如表2所示。柴油机主要由机体组、两大结构(曲柄连杆机构、配气机构)、五大系统(冷却系统、润滑系统、燃油供给系统、起动系统、进排气系统)组成。

表2 柴油机技术指标

实验台主要可分为柴油机系统和数据采集系统两个部分。实验台全景图如图10所示。振动信号数据采集系统由北京中科泛华公司生产的状态信息综合处理系统、PXI-3342型数据采集卡、B&W14100型压电式振动加速度传感器和Labview编写的采集软件组成,以实现对柴油机振动状态监测信号的采集和处理。

通过数据采集系统对正常状态下柴油机缸盖振动信号进行采集,振动加速度传感器安装位置如图11所示。

振动加速度传感器主要参数如表3所示,采样频率为20 kHz,单次采样时间为12 s,样本采样间隔为30 s。经过数据采集实验,有300组数据,每组数据有6个通道的数据,单次采样数据量为240 000。为了避免柴油机从启动到稳定状态过程中带来的误差,截取柴油机第5通道后5 000个采样点作为测试信号。

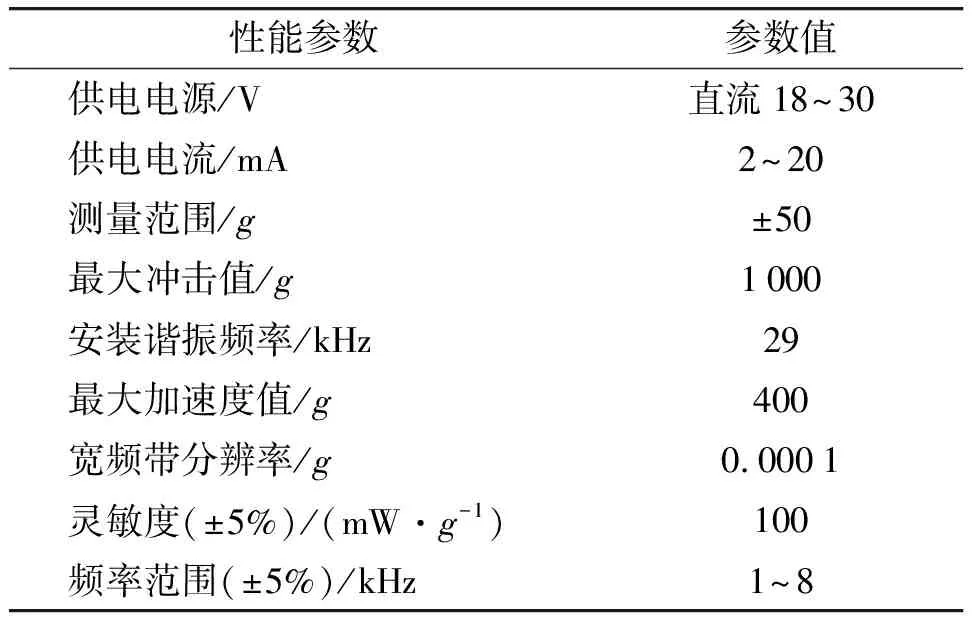
表3 振动加速度传感器主要参数

由于自行火炮柴油机的运行环境复杂,各个部件相互干扰,各种非线性、非平稳信号彼此严重重叠,采集到的振动信号不可避免地被噪声污染。为了减少噪声的不利影响,需要对原始信号进行降噪处理。通过不同的降噪方法对采集到的原始信号进行降噪处理后,原始信号及降噪结果如图12所示。

由于实际工程中,采集到的振动信号中噪声和有效信号的功率均未知,无法继续使用前文中的评价指标对不同方法的降噪效果进行判断。因此,将降噪误差比dnSNR引入,用于评价降噪效果,该值越小,表明降噪效果越好,表达式如下：

dnSNR=10lg(Ps/Pg),

(26)

式中,Ps和Pg分别表示含噪信号和降噪信号的功率。降噪效果评价指标的计算结果如表4所示。

表4 实验室实测数据的评价指标计算结果

由图12和表4可得,使用小波阈值降噪、多小波相邻系数降噪和ICEEMDAN-MPE-小波阈值3种对比方法降噪后的结果存在不同程度的降噪过度及降噪不完全现象,降噪效果不佳。将笔者所提降噪方法应用于自行火炮柴油机振动信号上时,无论从降噪结果图还是定量评价指标上,与目前广泛应用的对比方法相比均具有较好的降噪效果,降噪误差比分别降低了22.143 3、6.834 9和0.722 7。

因此,笔者所提自行火炮振动信号降噪方法的有效性得到了验证,与其他方法相比能够有效降低原始信号中的噪声。

4 结论

笔者以自行火炮为研究背景,对自行火炮柴油机的振动信号降噪方法展开研究。针对现有降噪方法存在降噪效果不理想、自适应差等问题,提出了一种更适用于自行火炮振动信号的降噪方法。可以得出以下结论：

1)仿真信号的降噪结果表明,所提方法能够在自适应滤除噪声的同时更好地保留信号中的真实成分,在信噪比、均方根误差和相关系数指标上均优于其他3种对比方法。

2)实测数据的结果表明,所提降噪方法应用于自行火炮柴油机时,与其他方法相比具有较好的降噪效果,能够有效且自适应地实现原始信号的降噪处理。

3)笔者所提的改进麻雀搜索算法能够实现对MPE中各参数自适应寻优,较为准确地筛选出所需的IMF分量。所提降噪方法可以为自行火炮的故障预测与健康管理研究提供理论与技术支撑,具有较好的工程应用前景。