PCMA系统双同步序列联合盲估计
李 放 邱钊洋 查 雄 李钟书 李天昀 张 昊
(信息工程大学信息系统工程学院,河南郑州 450001)
1 引言
成对载波多址(Paired Carrier Multiple Access,PCMA)是由美国ViaSat 公司提出的一种卫星通信频域复用多址技术[1],具有频带利用率高、抗截获能力强等特点,被广泛应用于军事和重要的商业通信系统。在PCMA 系统中,卫星地面站会在同一频率上接收到本地信号(自干扰信号)和远端地面站信号(有用信号)叠加后的混合信号。在合作通信中,地面站已知发送信号的全部内容和参数,因此可以采用干扰抵消的方法,达到正常通信的目的。在信号盲接收场景中,接收方无法获得任何先验信息,只能采用单通道盲分离的方法获得通信内容。
传统的PCMA 混合信号盲分离技术主要有粒子滤波[2]和逐幸存路径处理(Per-Survivor Processing,PSP)[3]两种经典算法。此外,为降低分离算法复杂度,Gibbs采样[4]、迭代量子遗传优化算法[5]、堆栈算法等[6]相继被应用于PCMA 信号盲分离。此类传统算法需要精确的参数估计结果作为初始化参数,否则会严重影响算法性能。随着深度学习技术的发展,神经网络也被应用于PCMA 信号解调中[7-9]。此类基于深度学习的盲分离方法同样需要精确的参数估计结果作为网络初始化参数。
在PCMA 信号参数估计算法中,使用同步序列作为数据辅助的参数估计方法[10-11]相较非数据辅助的方法[12-14]具有精度高、鲁棒性好等明显优势,更利于盲分离算法的收敛。然而同步序列在信号的盲接收中同样为未知条件,因此本文聚焦PCMA 信号的同步序列盲估计问题,旨在提出一种PCMA 信号双同步序列盲估计方法。在PCMA 通信系统中,幅相调制(Amplitude-Phase Modulation,APM)使用最为广泛,如BPSK,QPSK,8PSK,8QAM,16QAM 等,因此本文的研究对象为采用APM调制的PCMA信号。
对于传统的单载波信号,盲解调算法比较成熟,可以利用解调结果得到同步序列估计;而PCMA 信号是由两路APM 信号线性叠加而成的同频混叠信号,且两路信号之间存在频差、相位差、时延差、幅度差,尚未形成成熟的盲分离方案,尤其是高阶调制的PCMA 信号目前难以实现盲分离,因此只能立足无法实现解调的条件,直接利用原始信号波形估计两路信号的同步序列。当前,国内外鲜有文献针对此问题开展研究,文献[10-11]等数据辅助的参数估计方法,往往将同步序列作为已知条件,而并未给出其估计方法。因此获得精确的同步序列盲估计,是数据辅助的PCMA 信号调制参数盲估计方法迈向工程实践道路上亟待解决的难题,具有较高的现实意义和研究价值。
为获取PCMA 信号同步序列盲估计,本文提出了一种双同步序列联合盲估计算法,在调制速率已知的条件下,推导PCMA 信号符号帧长与信号自相关函数的关系,通过搜索自相关函数峰值,得到对两路APM 信号符号帧长的估计;对信号按帧长分段,利用奇异值分解(Singular Value Decomposition,SVD)理论[15],对自相关矩阵做整体SVD分解,推导矩阵特征值、特征向量与信号同步波形之间的近似数学关系,重点分析了不同信号参数下分解结果的差异,给出了每种情况下同步波形估计方法,实现了对两路APM 信号同步波形及其位置的粗略估计;在此基础上对同步波形位置的原始PCMA 信号做局部SVD分解(即“先整体后局部”),得到更高精度的同步波形估计,解调同步波形即可得到同步序列估计,解决了PCMA 信号盲接收中双同步序列估计的难题;在整体SVD 分解的基础上,对比局部SVD 分解估计方法与最大似然(Maximum-Likelihood,ML)估计方法[16],评估了算法性能。
2 信号模型
采用两路幅相调制信号混合的PCMA 信号复基带模型,可以表示为
式中h1(t)和h2(t)分别是两路APM 信号的瞬时幅度;ω1和ω2分别是两路信号的残留载波角频率;θ1和θ2分别是两路信号的初始相位;v(t)为实部与虚部统计独立的加性高斯白噪声,方差为;a1(t)和a2(t)分别为两路APM 信号的基带调制信号,可表示为
式中αi(n)表示第i路APM 信号发送的第n个符号;gi(t)为包括成形滤波器、信道滤波器和匹配滤波器等在内的等效信道滤波器的脉冲响应;T为符号周期,两路信号相同;τi(t)为第i路信号与本地参考时钟之间的相对时间延迟。
假设等效信道滤波器响应具有有限的持续时间[-L1T,L2T],L=L1+L2+1,且每路信号的瞬时幅度和相对时延在一段时间内恒定,即hi(t)=hi,τi(t)=τi。对混合信号y(t)以时间间隔Ts=T/p进行采样,p为过采倍数,是一个正整数,可得到其过采样的离散形式
定义k时刻第i路APM信号的符号向量为
第i路APM 信号的等效滤波器脉冲响应向量为
则xk(l)可表示为向量乘法的形式
3 算法原理
3.1 帧长估计
当卫星通信双方传输的比特流数据具有帧结构时,一般具有固定的同步比特和数据帧长度,则经过APM 调制后得到的基带符号也具有固定的同步符号和符号帧长,进而信号的过采样形式也具有同步波形和过采样帧长。PCMA 混合信号符号帧结构如图1 所示,Hi为第i路APM 信号同步符号长度,ni为第i路APM信号同步符号起始位置。
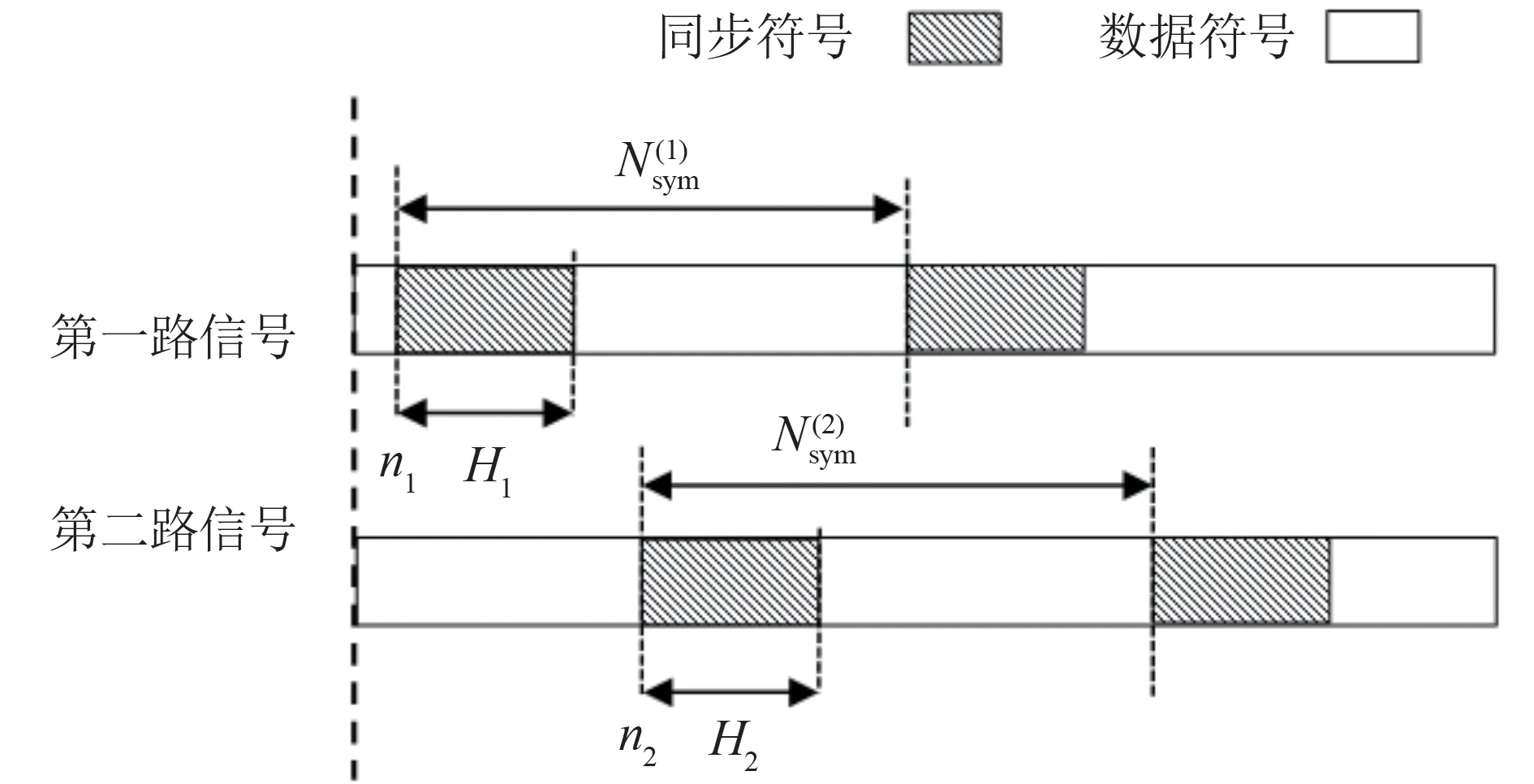
图1 PCMA混合信号符号帧结构示意图Fig.1 Scheme of PCMA-signal symbol-frame structure
取长度为Nr的过采样PCMA 混合信号样本yk(l),当数据长度Nr足够大时,其自相关函数Ry(k)的估计可表示为
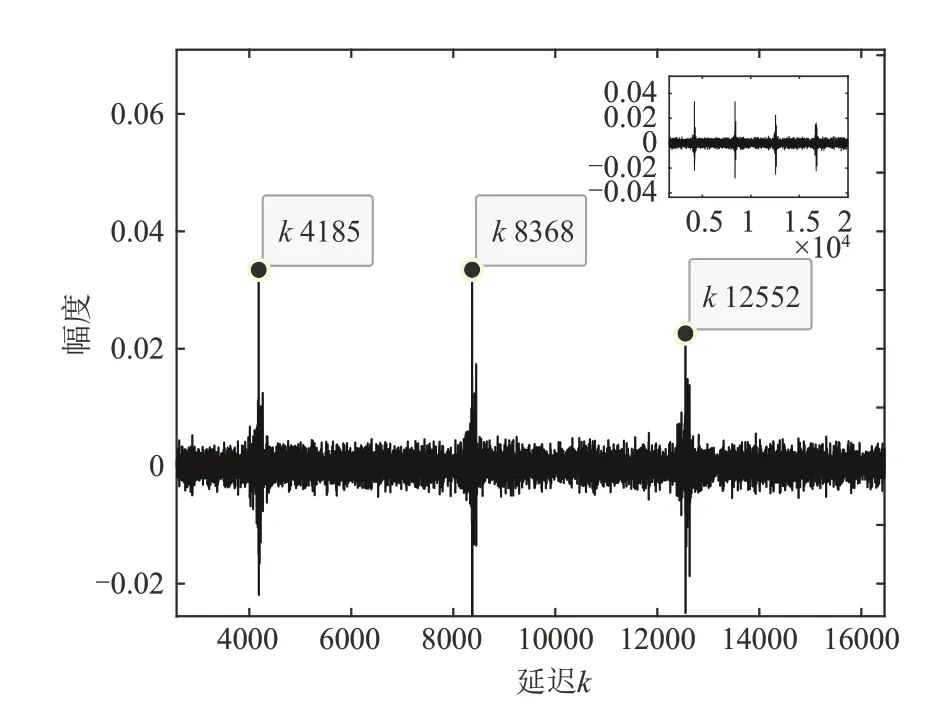
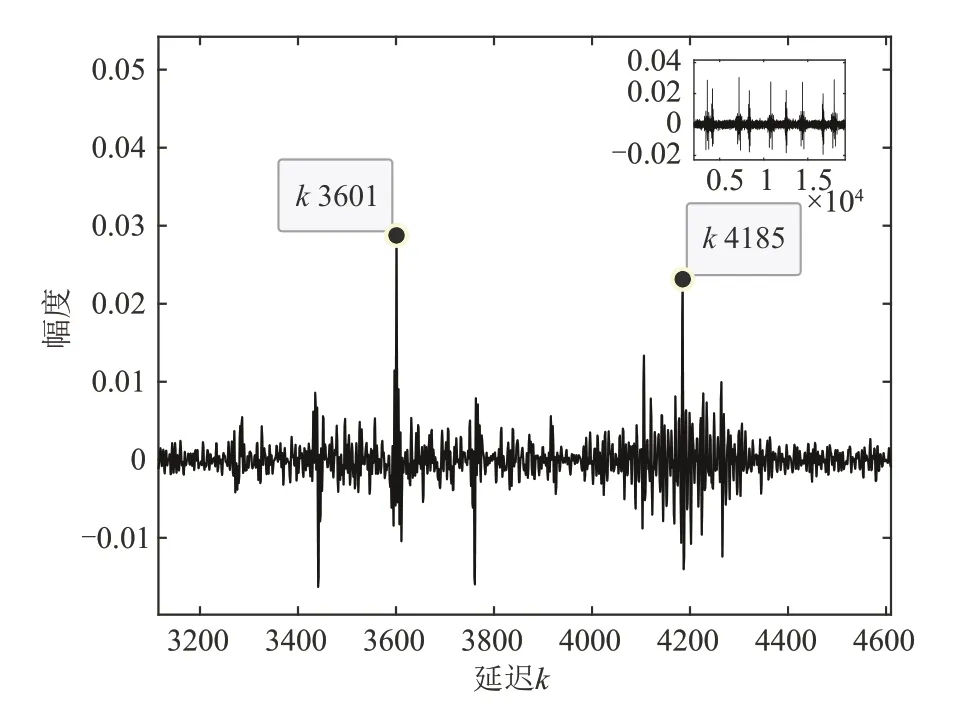
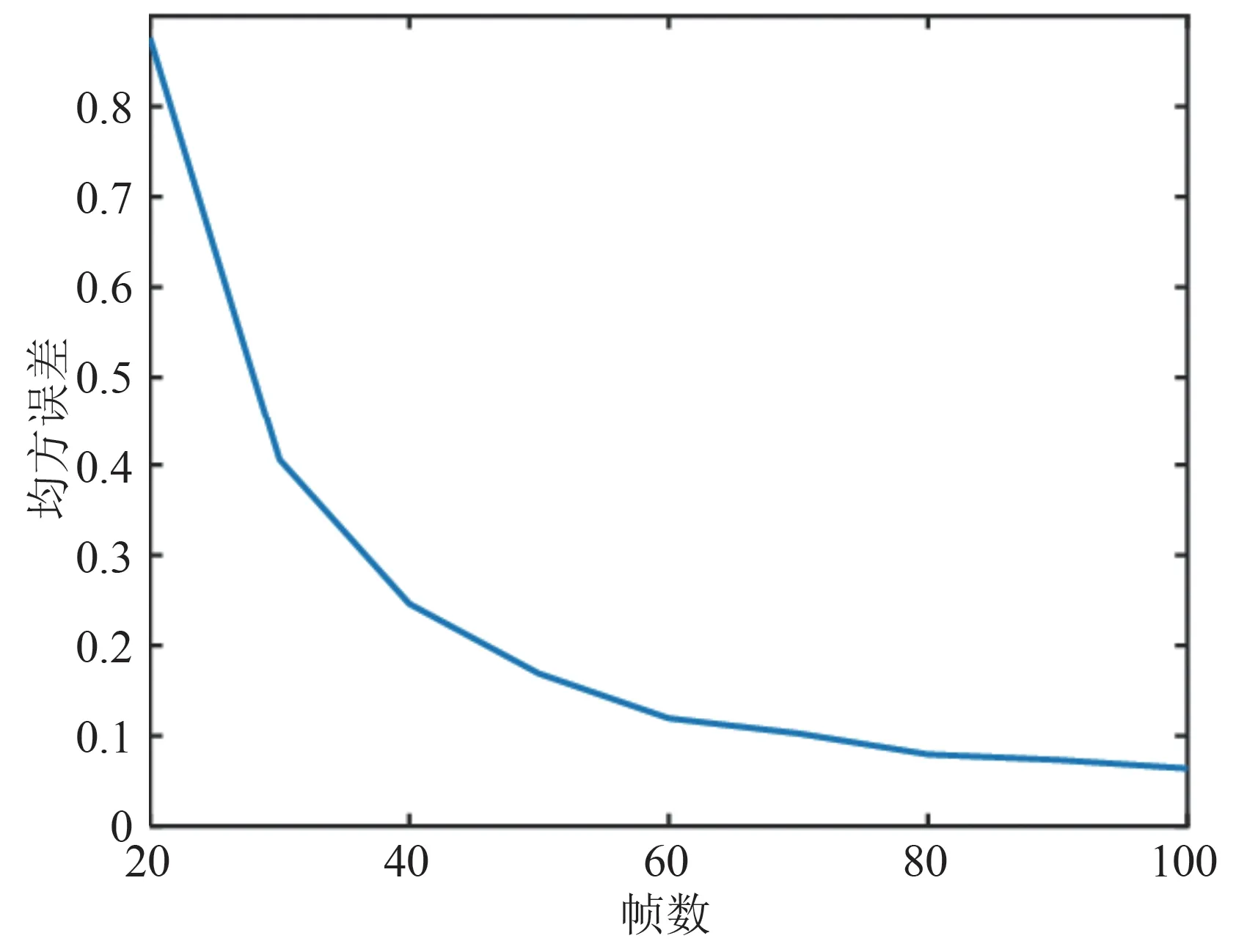
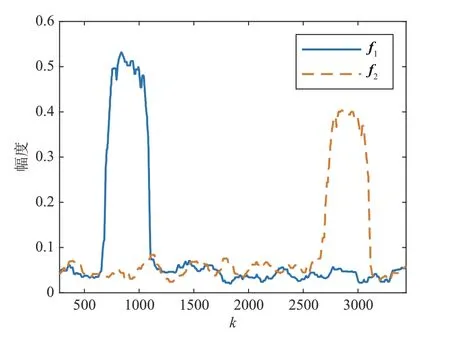
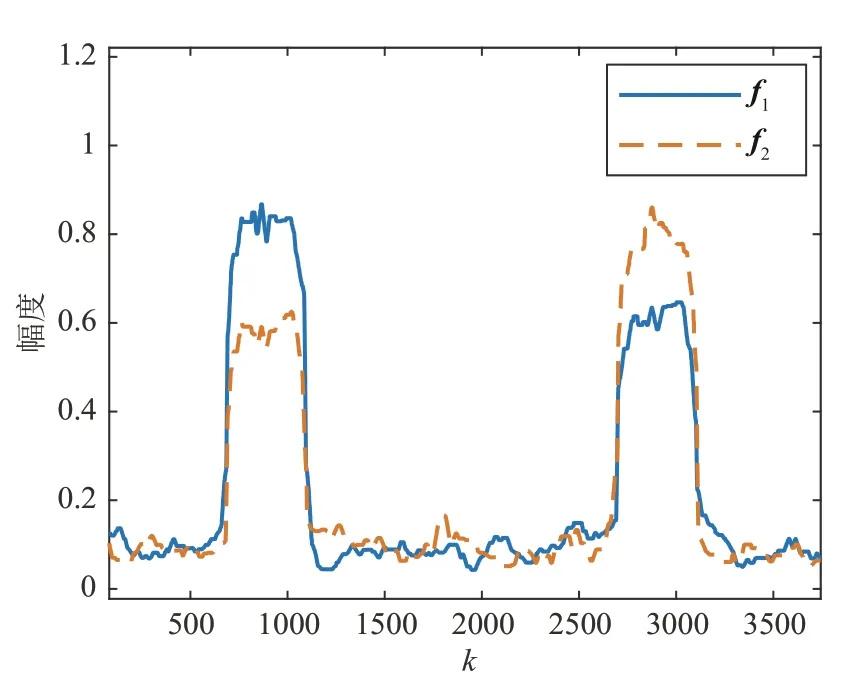
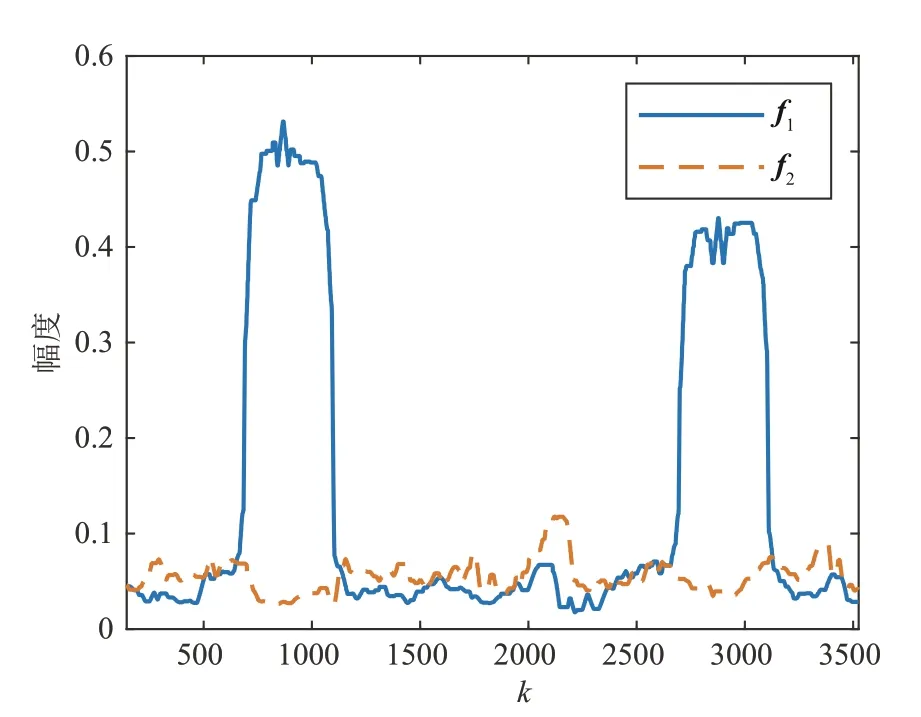
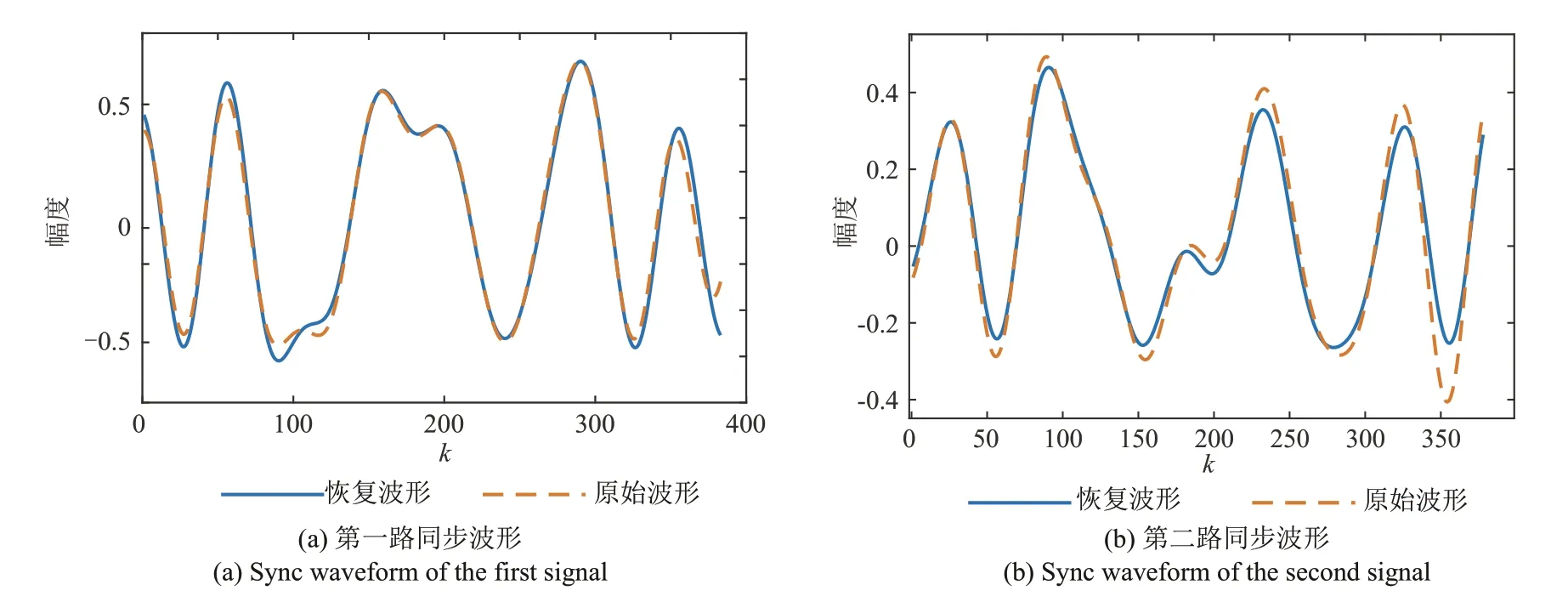
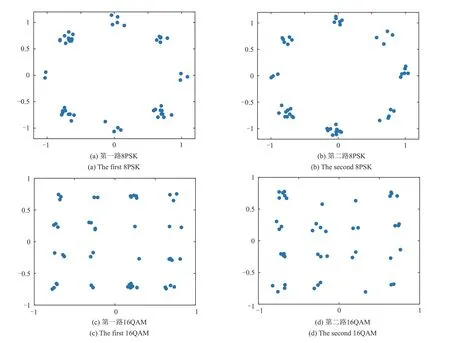
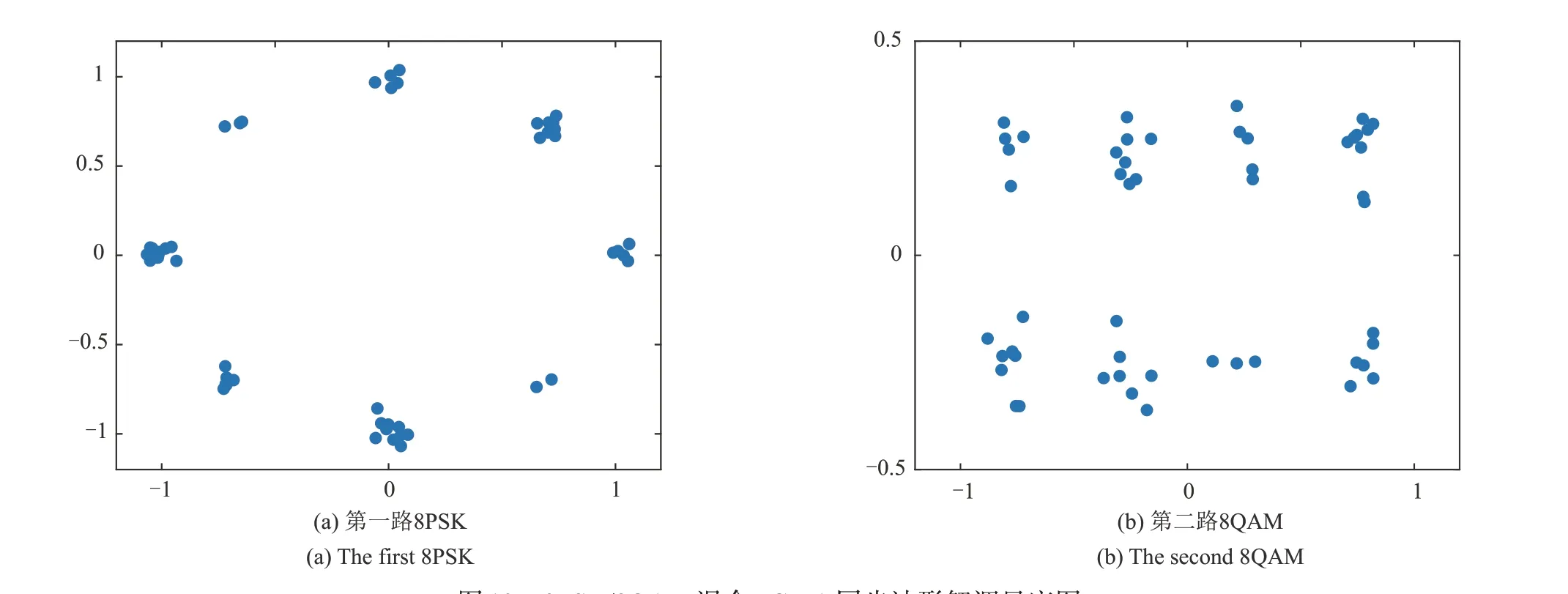
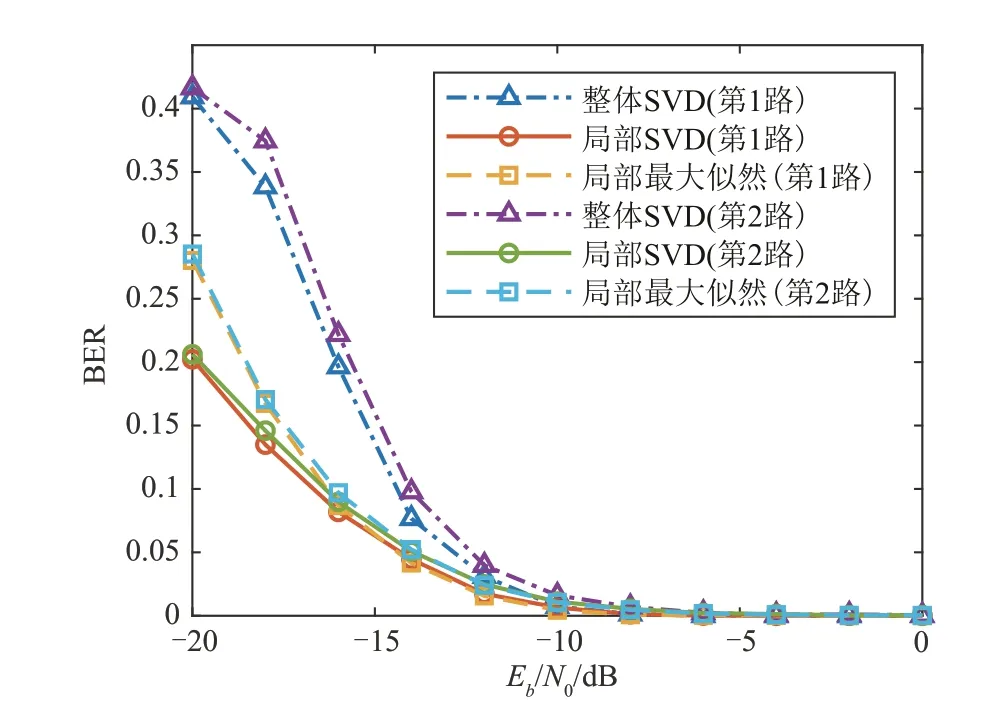
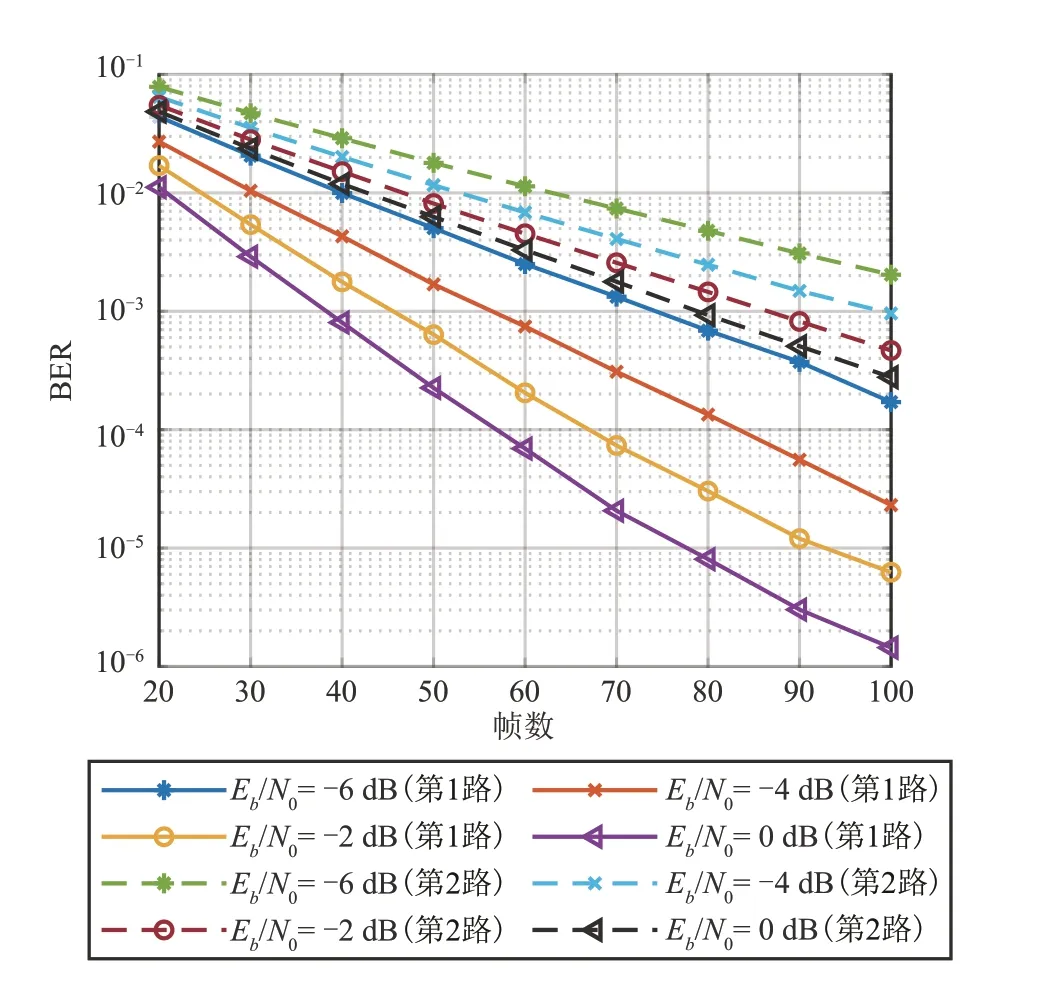
式中k=0,1,…,Kr,1 ≪Kr 对于结构如图1所示的PCMA信号,一般认为两路APM 信号具有相同的符号帧长,过采样帧长N=pNs,第n帧过采样信号向量可表示为 式中n=0,1,…;xn=[xn,0(0),…,xn,Ns-1(p-1)]Τ,为第n帧有用信号向量,其中xn,k(l)=xnNs+k(l);vn=[vn,0(0),…,vn,Ns-1(p-1)]Τ,为第n帧高斯白噪声向量,其中vn,k(l)=vnNs+k(l)。 定义向量yn的自相关矩阵为 式中m≤min(P,N),σ1≥σ2≥…≥σm是数据矩阵A的奇异值,且为大于零的实数。相关矩阵R的估计为 将式(7)代入上式中可得 式中0 ≤l1,l2≤p-1,0 ≤k1,k2≤Ns-1。 假设两路APM 信号异步,即同步符号在时间上没有重叠,在一帧数据中,两路信号同步符号位置区间为 当k1∉或,且pk1+l1≠pk2+l2,即k1≠k2或l1≠l2时,由于非同步部分数据随机分布,则对于不同的帧数n,xn,k1(l1),xn,k2(l2)之间互不相关,当数据量P足够大时 此时 可以证明当pk1+l1=pk2+l2,即k1=k2且l1=l2时,可得到与式(19)相同的结果。 当pk1+l1≠pk2+l2,即k1≠k2或l1≠l2时 若(ω1-ω2)NTs=2mπ,m=0,±1,±2… 将式(16)~式(24)代入式(15)中,可以得到当(ω1-ω2)NTs=2mπ时,近似认为 当(ω1-ω2)NTs≠2mπ时,近似认为 式中Λ′为对角线矩阵。且有 式中φ1-φ2=θ1-θ2。则得到对b1和b2的估计,即可得到对两路信号同步波形及其存在位置的估计。 在式(11)及上述推导中,假设了数据起点k=0,l=0,事实上对数据按帧长分段时,在保证一帧数据包含完整的同步波形的前提下,改变起点位置,推导结果类似。 当(ω1-ω2)NTs=2mπ 时,自相关矩阵的能量分布如图2(a)所示,主要能量集中在矩阵对角线和两路APM信号同步波形自相关运算及互相关运算的位置;当(ω1-ω2)NTs≠2mπ时,自相关矩阵的能量分布如图2(b)所示,主要能量集中在矩阵对角线和两路APM信号同步波形自相关运算的位置。 图2 相关矩阵能量等线分布图Fig.2 Correlation-matrix energy-contour distribution diagram 分解结果1当(ω1-ω2)NTs=2mπ时,自相关矩阵存在式(25)中的近似等式关系,对于式中(b1+b2)(b1+b2)H项,根据矩阵分解理论,存在如下关系 其中λ为矩阵(b1+b2)(b1+b2)H的特征值,矩阵的特征向量为b1和b2的线性组合(b1+μb2),μ为实数。令h2=ηh1,b1=h1a1,b2=h2a2,,μ′=ημ,则式(28)可以重新表示为 解上式方程得到 当(ω1-ω2)NTs≠2mπ 时,自相关矩阵存在式(26)中的近似等式关系,对于式中项,根据矩阵分解理论,存在如下关系 同理可化简得到方程 解上式方程,可以得到两种情况。 实际信号中,此类情况一般发生在η≈1 且两路同步波形总能量相等时,但由于受到矩阵中后两项Λ′和Ι的影响,矩阵分解可能不会得到完全相等的二重根,特征值和特征向量有较大随机性,上述方法不再成立,但此时仍满足 将式(37)代入式(36)中可以得到 通过以上方法可以分别得到两路APM 信号的同步波形 PCMA 信号在第i路信号的第n帧同步波形区间取值可表示为 其中n=0,1,2,…。由于两路APM 信号统计独立,zi,k(l)和(l)的互相关可以按下式计算 综上,通过SVD 对数据自相关矩阵分解,解得向量b1,b2,即可得到对两路APM 信号同步波形及其在数据帧中的位置的估计(向量非零部分数据即为同步波形,非零数据所在位置即为同步波形位置),同步波形估计为常规单载波信号,易于实现解调,解调同步波形即可得到双路同步序列估计。 在上述推导中,采用了较多的近似计算,因此利用上述SVD 分解方法得到的同步波形估计存在一定的性能损失,因此得到两段同步波形位置的估计后,可分别取出两路信号同步波形位置的原始PCMA 混合信号(由一路信号的同步波形和另一路信号的非同步波形叠加而成),构造相关矩阵做SVD 分解,得到更精确的同步波形估计,其推导过程类似,本文不再证明。 根据前文内容给出算法步骤如下: Step1取长度为Nr的过采样PCMA 混合信号样本yk(l),计算自相关函数估计(k),搜索自相关函数峰值,得到第i路信号对应所有峰值的近似最大公约数,则符号帧长。对于一般的PCMA 信号,,N=pNs,N为过采样帧长,p为过采倍数。 Step2按帧长N对PCMA 信号分段,得到数据矩阵A及其自相关矩阵估计(P)。对(P)做SVD 矩阵分解(整体SVD 分解),得到最大的两个特征值及其各自对应的特征向量 Step4根据Step3 的分解结果,可得到对两段同步波形位置的粗略估计,即特征向量,中具有较高能量包络的两段位置。分别对两段同步波形位置的原始PCMA 混合信号,按帧累积得到自相关矩阵并做SVD 分解(局部SVD 分解),获取更高精度的同步波形和同步序列估计。 为验证本文算法的有效性,分别设计实验估计PCMA 信号帧长、同步波形,对同步波形解调得到双同步序列,并通过同步序列估计误比特率,验证估计性能。 实验1以QPSK调制PCMA混合信号为例,仿真条件为:采样率20 MHz,符号速率5 MBd,升余弦滤波器滚降系数0.35,两路QPSK信号符号帧长1046,同步符号长度52,幅度分别为h1=0.5,h2=0.4,频偏分别为f1=500 Hz,f2=-500 Hz,时延分别为τ1=0.1T,τ2=0.5T,在混合信号信噪比Es/N0=12 dB下,对混合信号做20000个采样点自相关,仿真结果如图3所示。 图3 等帧长混合信号时域自相关局部展开Fig.3 Autocorrelation local expansion of PCMA signals with equal frame lengths 从图中可以看出,混合信号自相关函数在过采样帧长(4184)的整数倍位置附近出现峰值。调整第二路QPSK 信号的符号帧长为900,另一路信号参数不变,仿真结果如图4所示。 图4 不同帧长混合信号时域自相关局部展开Fig.4 Autocorrelation local expansion of PCMA signals with different frame lengths 从图中可以看出,混合信号自相关函数除了在第一路信号过采样帧长的整数倍位置附近出现峰值外,在第二路信号过采样帧长的整数倍位置附近也出现峰值。调整第二路信号调制方式为BPSK,保持符号帧长为900,其他参数不变,仿真结果如图5 所示。从图中可以看出,混合信号自相关函数的峰值出现位置和图4中一致。 图5 混合调制信号时域自相关局部展开Fig.5 Autocorrelation local expansion of mixed modulated signals 实验1 结果表明,无论PCMA 混合信号包含的两路信号帧长、调制方式是否相同,采用自相关函数峰值搜索方法,都能够有效估计符号帧长。 实验2为验证自相关长度Kr对帧长估计性能的影响,以QPSK 调制PCMA 混合信号为例,使用不同帧数的数据做自相关。仿真条件为:采样率20 MHz,符号速率5 MBd,升余弦滤波器滚降系数0.35,两路QPSK 信号符号帧长1046,同步符号长度52,幅度分别为h1=0.5,h2=0.4,频偏分别为f1=500 Hz,f2=-500 Hz,时延分别为τ1=0.1T,τ2=0.5T,混合信号信噪比Es/N0=6 dB。kn表示自相关函数第n个峰值的位置,1 图6 不同数据量下帧长估计的均方误差Fig.6 Mean square error of frame-length estimation under different data volumes 从图中可以看出,随着自相关长度的增加,帧长估计的均方误差不断降低,在较低信噪比下使用60 帧以上数据均方误差达到0.2 以下,能够得到正确的帧长估计。 实验3以8PSK调制PCMA信号为例,采样率125 MHz,符号速率5 MBd,升余弦滤波器滚降系数0.35,持续时间8 个符号长度,两路8PSK 信号符号帧长700,同步符号长度16,同步符号起始位置分别为第20个符号和第100个符号,幅度分别为h1=0.5,h2=0.4,频偏分别为f1=500 Hz,f2=-500 Hz,时延分别为τ1=0.1T,τ2=0.5T,混合信号信噪比Es/N0=15 dB,取200 帧长度数据,SVD 分解(整体SVD)结果如图7所示。 图7 有频差幅度不相等条件下SVD分解主特征向量包络Fig.7 Principal eigenvector envelope of SVD under thecondition of frequency offset and unequal amplitudes 图中横坐标k表示采样时刻,,分别等于数据自相关矩阵第一、第二特征值开根号乘以特征向量,对应(ω1-ω2)NTs≠2mπ 且的情况。从幅度包络图中可以看出,f1,f2分别在两路8PSK 信号同步波形部分呈现较高的幅度值,约为0.5 和0.4,与原始信号包络幅度相近。由此可知通过SVD 分解得到的向量可以估计同步波形位置和两路信号幅度。 幅度条件设置为h1=h2=1.0,分解结果如图8所示。图中的幅度包络对应于(ω1-ω2)NTs≠2mπ且情况。从图中可以看出,b1,b2在f1,f2中均有能量分布,且ρ1≈0.8,ρ2≈0.6,,满足式(38)推导,实际上这也是能量守恒的表现,b1,b2在f1,f2中分布的能量和等于各自总能量。 图8 有频差幅度相等条件下SVD分解主特征向量包络Fig.8 Principal eigenvector envelope of SVD under the condition of frequency offset and equal amplitudes 调整两路频偏f1=f2=0 Hz,分解结果如图9 所示。图中幅度包络对应(ω1-ω2)NTs=2mπ 情况,此时f1=b1+b2,同步波形全部包含于向量f1中。 图9 无频差条件下SVD分解主特征向量包络Fig.9 Principal eigenvector envelope of SVD without frequency offset 在初始条件下,矫正同步波形相位,与原信号波形比较,仿真实验结果如图10所示。图中虚线为真实信号波形,实线为根据本文算法恢复的波形,从图中可以看出采用本文方法,可以对同步波形有效恢复。 图10 波形恢复结果Fig.10 Waveform recovery results 实验4对采用8PSK、16QAM 等调制方式的PCMA 混合信号使用本文方法,获取同步波形,解调得到同步序列,仿真条件为:采样率20 MHz,符号速率5 MBd,升余弦滤波器滚降系数0.35,幅度分别为h1=1.0,h2=0.8,频偏分别为f1=500 Hz,f2=-500 Hz,时延分别为τ1=0.1T,τ2=0.5T,所有调制方式信号符号帧长均设置为1024,同步符号长度52。 在混合信号信噪比Es/N0=10 dB 条件下,使用200 帧数据做SVD 分解(整体SVD),同步波形解调星座图如图11所示。 图11 不同调制方式同步波形解调星座图Fig.11 Constellations of sync waveform demodulations of different modulations 从解调星座图可以看出,利用本文方法估计得到的同步波形,能够有效恢复同步序列。 PCMA 信号改为8PSK/8QAM 混合调制方式,其他条件不变,仿真结果如图12所示。从同步波形解调星座图可以看出,本文算法对采用混合调制方式的PCMA信号同样有效。 图12 8PSK/8QAM混合PCMA同步波形解调星座图Fig.12 8PSK/8QAM hybrid PCMA sync waveform demodulation constellation 为验证算法性能,以16QAM 调制的PCMA 信号为例,使用100 帧数据对PCMA 混合信号在不同信噪比下做同步序列估计,首先对信号按帧分段,做整体SVD 分解,得到同步波形位置估计,再分别利用SVD 分解方法和最大似然方法[16]针对同步波形位置的混合数据做局部处理得到同步波形,进而解调得到同步序列估计,两路信号同步序列估计误比特率曲线如图13所示。图中横坐标Eb/N0代表单路信号每比特能量与高斯白噪声功率密度的比值。 图13 不同信噪比下两路16QAM信号同步波形解调误比特率曲线Fig.13 Bit error rate curve of sync waveform demodulation of the two 16QAM signals versus Eb/N0 从图13 中可以看出,局部SVD 分解方法和局部最大似然方法,较整体SVD 分解方法,估计性能有明显提升;在低信噪比条件下,局部SVD 分解方法较局部最大似然方法更优,在较高信噪比条件下两者性能相近。 为验证数据量对算法性能的影响,仍以16QAM调制的PCMA 信号为例,在不同信噪比条件下,利用不同帧数的数据,按照先整体后局部SVD分解的方法得到同步波形,解调得到同步序列估计,两路信号同步序列估计误比特率曲线如图14所示。 图14 不同数据量下两路16QAM信号同步波形解调误比特率曲线Fig.14 Bit error rate curve of synchronous waveform demodulation of the two 16QAM signal versus data volume 实验4 结果表明,本文方法能够有效估计采用单一APM 调制方式和混合APM 调制方式的PCMA信号同步波形,进而得到双同步序列估计,且在低信噪比条件下相对于最大似然的估计方法效果更优,随着信噪比的提升和使用数据量的增加,估计误码率不断降低,能够得到高精度的PCMA 信号双同步序列盲估计。 本文在PCMA 信号盲分离场景下,在调制速率已知的基础上,提出一种PCMA 系统双同步序列联合盲估计算法,推导PCMA 信号符号帧长和PCMA混合信号自相关函数的关系,通过搜索自相关函数峰值,得到对两路APM 信号符号帧长的估计;将奇异值分解理论应用于PCMA 信号盲分离问题中,推导自相关矩阵特征值、特征向量与信号同步波形之间的对应关系,重点分析了频偏、同步波形总能量等参数对分解结果的影响,得到不同条件下对两路APM 信号同步波形的估计方法,并提出“先整体后局部”的分解流程进一步提高了估计精度,在不同信噪比和数据量条件下解调同步波形得到同步序列估计,并与最大似然估计方法对比,从仿真结果可以看出,在低信噪比条件下本文方法优于最大似然估计方法,在高信噪比条件下与最大似然估计方法效果相近,随着信噪比的提升和使用数据量的增加,估计误比特率不断降低,能够得到对PCMA 信号双同步序列的高精度估计,为数据辅助的参数估计方法应用于工程实践提供了先决条件,为PCMA 信号调制参数估计和后续的盲分离技术研究提供重要基础。3.2 同步序列估计

3.3 算法流程
4 仿真分析

5 结论